冀教版数学八年级上册单元检测卷 第十三章 全等三角形(测能力)(含解析)
文档属性
| 名称 | 冀教版数学八年级上册单元检测卷 第十三章 全等三角形(测能力)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 22:44:17 | ||
图片预览



文档简介
全等三角形
(测能力)
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.如图,已知,,,则的度数为( )
A.75° B.65° C.40° D.30°
2.下列命题:①同旁内角互补,两直线平行;
②若,则;
③末位数字是5的数,能被5整除;
④对顶角相等.
逆命题是假命题的个数是( )
A.1个 B.2个 C.3个 D.4个
3.数学课上陈老师要求学生利用尺规作图,作一个已知角的角平分线,并保留作图痕迹.学生小敏的作法是:如图,是已知角,以O为圆心,任意长为半径作弧,与、分别交于N、M;再分别以N、M为圆心,大于的长为半径作弧,交于点C;作射线;则射线是的角平分线.小敏作图的依据是( )
A. B. C. D.
4.如果所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店配一块完全一样的玻璃,那么最省事的办法是带( )去.
A.① B.② C.③ D.①和②
5.如图所示,锐角中,D,E分别是,边上的点,,,且,、交于点F,若,则的度数为( )
A.110° B.105° C.100° D.95°
6.如图为6个边长相等的正方形的组合图形,则( )
A. B. C. D.
7.如图,,,,点B,D,E在同一直线上,若,,则的度数是( )
A. B. C. D.
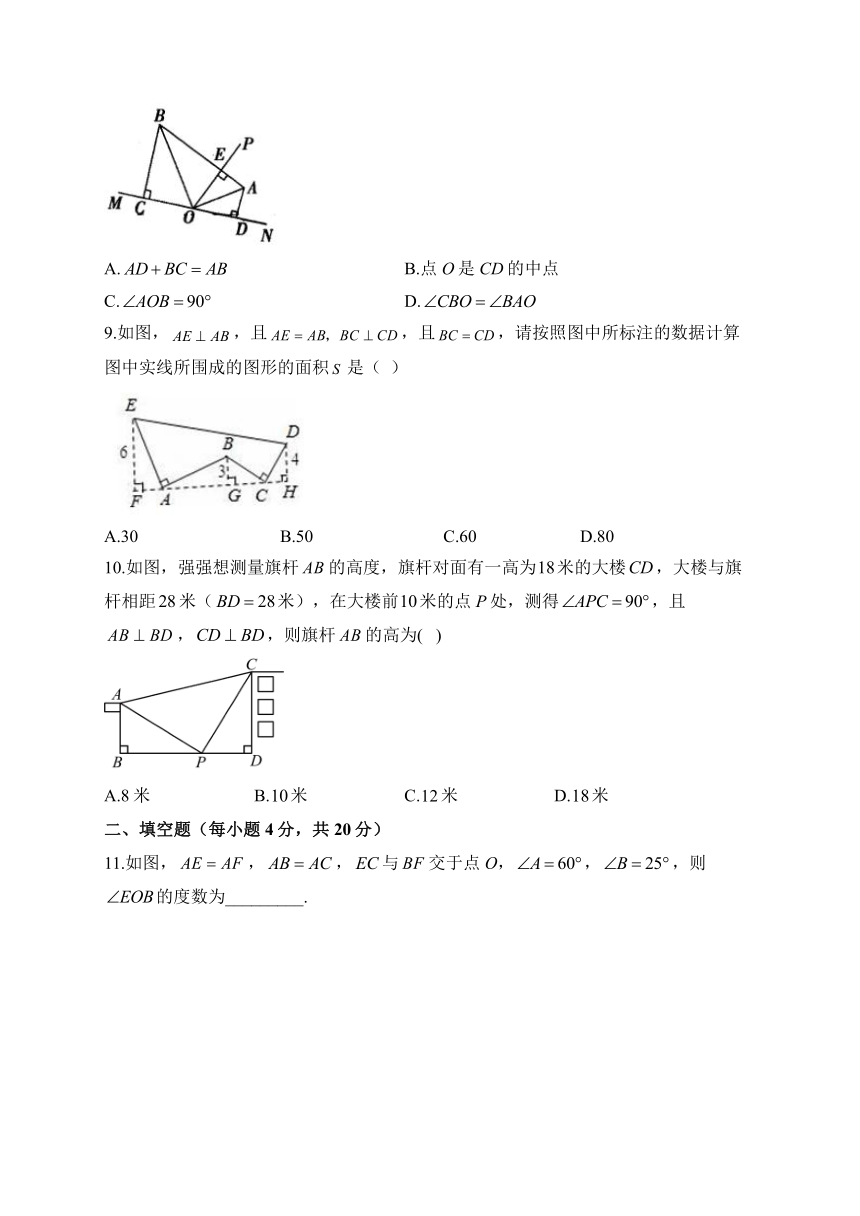
8.如图,OA平分,平分,于点E,于点C,于点D,下列结论错误的是( )
A. B.点O是CD的中点
C. D.
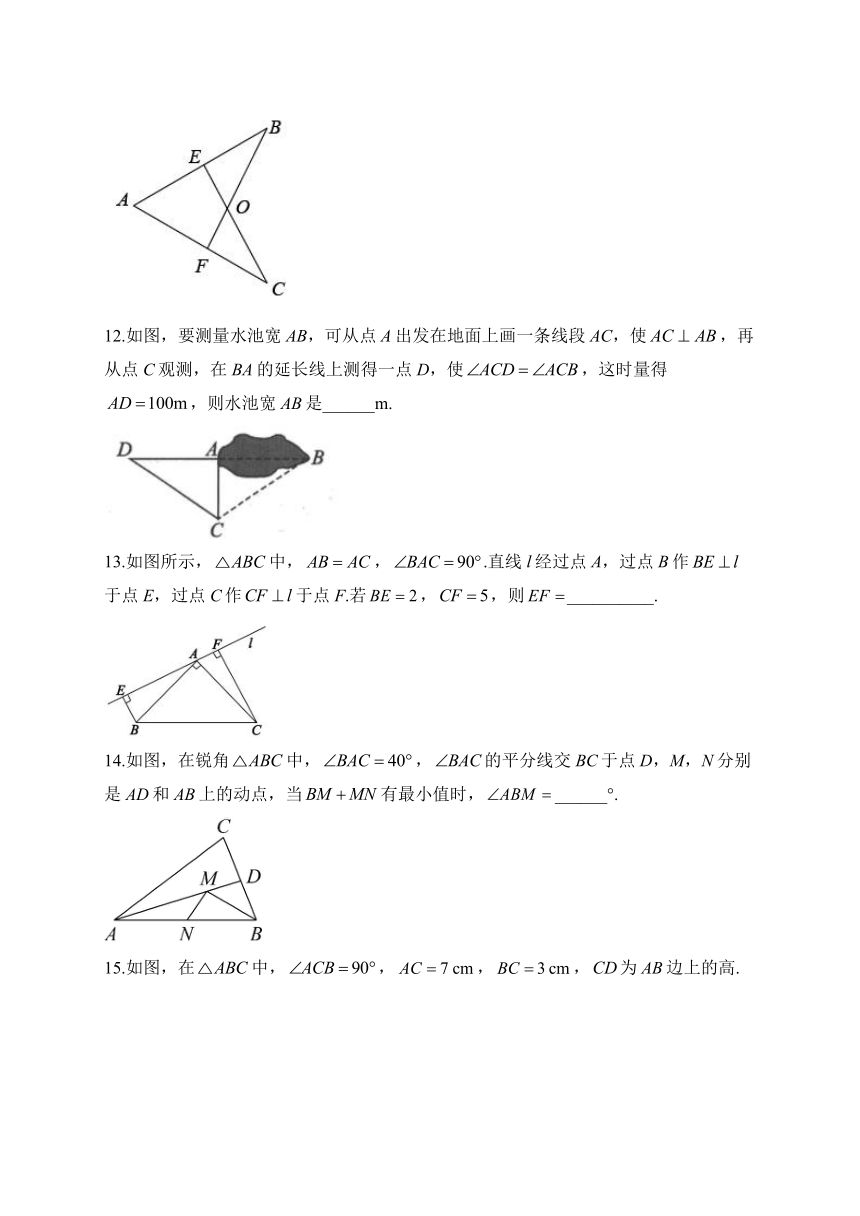
9.如图,,且,且,请按照图中所标注的数据计算图中实线所围成的图形的面积是( )
A.30 B.50 C.60 D.80
10.如图,强强想测量旗杆的高度,旗杆对面有一高为米的大楼,大楼与旗杆相距米(米),在大楼前米的点P处,测得,且,,则旗杆的高为( )
A.8米 B.米 C.米 D.米
二、填空题(每小题4分,共20分)
11.如图,,,与交于点O,,,则的度数为_________.
12.如图,要测量水池宽AB,可从点A出发在地面上画一条线段AC,使,再从点C观测,在BA的延长线上测得一点D,使,这时量得,则水池宽AB是______m.
13.如图所示,中,,.直线l经过点A,过点B作于点E,过点C作于点F.若,,则__________.
14.如图,在锐角中,,的平分线交BC于点D,M,N分别是AD和AB上的动点,当有最小值时,______°.
15.如图,在中,,,,为AB边上的高.
(1)若点E在BC延长线上,点F在DC延长线上,且,则____________(用含的式子表示);
(2)若点E从点B出发,在直线BC上以的速度移动,过点E作BC的垂线交直线CD于点F,当点E运动__________s时,.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,已知,.
(1)求CD的长.
(2)AB与DE平行吗?为什么?
解:(1)(已知),
(___________),
(等式性质)
即________=__________
_________
(2)(已知)
_______(___________)
__________(__________)
17.(8分)如图,有一条河流(假设河流两岸平行,即),由于河水湍急,无法下水,为了测量河的宽度,林师傅给出了以下方法:
①在河岸b上确定点A(如图),利用红外线光束,在河岸a上确定点B,使得与河岸垂直;
②从A点沿河岸向东直走,记为点C(如图),继续向东直走,到达点D;
③从D点沿垂直河岸的方向行走,行走过程中,用红外线光束一直对准B,当点C刚好出现在红外线光束上时,停下,记为点E;
④测得的长为.
(1)根据上述方法,河流的宽度为______m;
(2)请你根据林师傅的方法,利用三角板和刻度尺,在图中画出B,D,E的位置,并结合题意说明林师傅作法的科学性.
18.(10分)已知:,,.
(1)如图1当点D在AB上,________.
(2)如图2猜想与的面积有何关系?请说明理由.(温馨提示:两三角形可以看成是等底的)
19.(10分)已知(如图),用三种不同的方法作,使.你认为哪一种作法比较简便?
20.(12分)【阅读理解】
课外兴趣小组活动时,老师提出了如下问题:
如图1,中,若,,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使,请根据小明的方法思考:
(1)由已知和作图能得到的理由是_____.
A.SSS B.SAS C.AAS D.HL
(2)求得AD的取值范围是______.
A. B. C. D.
【感悟】
解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
【问题解决】
(3)如图2,AD是的中线,BE交AC于E,交AD于F,且.求证:.
21.(12分)在练习课上,慧慧同学遇到了这样一道数学题:如图,把两个全等的直角三角板的斜边重合,组成一个四边形ACBD,,以D为顶点作,交边AC,BC于点M,N,,连接MN.
探究AM,MN,BN三条线段之间的数量关系.
慧慧分析:可先利用旋转,把其中的两条线段“接起来”,再通过证明两三角形全等,从而探究出AM,MN,BN三条线段之间的数量关系.
慧慧编题:在编题演练环节,慧慧编题如下:
如图(1),把两个全等的直角三角板的斜边重合,组成一个四边形,,以D为顶点作,交边AC,BC于点M,N,,连接MN. (1)先猜想AM,MN,BN三条线段之间的数量关系,再证明. (2)绕点D旋转,当M,N分别在CA,BC的延长线上,完成图(2),其余条件不变,直接写出AM,MN,BN三条线段之间的数量关系.
请你解答:请对慧慧同学所编制的问题进行解答.
答案以及解析
1.答案:B
解析:,
,,
,故选B.
2.答案:C
解析:①同旁内角互补,两直线平行的逆命题是两直线平行,同旁内角互补,是真命题;
②若,则的逆命题是若,则;也可以是所以是假命题;
③末位数字是5的数,能被5整除逆命题是能被5整除的数,末位数字是5;末尾数也可以是0,所以是假命题;
④对顶角相等的逆命题是相等的角是对项角,是假命题;
它们的逆命题是假命题的个数是3个.故选C.
3.答案:D
解析:由作图可知,,
又,
,,
,
平分.
故选:D.
4.答案:C
解析:①仅保留了原三角形的一个角和部分边,不符合任何全等三角形判定方法;②仅保留了原三角形的一部分边,所以该块不行;
③不但保留了原三角形的两个角还保留了其中一个边,所以符合判定,所以应该拿这块去.
故选:C.
5.答案:A
解析:设,
,,
,,,
,,
,
,,
,即,则,
,
.
故选:A.
6.答案:B
解析:在和中,
,
,
,
,
,
,
,
故选B.
7.答案:C
解析:,
,
,
,,
,,
,,
,,
.
故选:C.
8.答案:D
解析:平分,平分,,,,故选项C不合题意.在和中,,,,.同理可得,,,,点O是CD的中点,故选项A,B不合题意.选D.
9.答案:B
解析:,,
,
在和中,
,,
同理,
,,,,
梯形DEFH的面积,
,,
图中实线所围成的图形的面积,
故选B.
10.答案:B
解析:由题意得,,,,
,
,
,,
,
,
,
,
,
在和中,
,
,
,
故选:B.
11.答案:
解析:,,,
,,
,
,,,,
,
,
.
故答案为:
12.答案:100
解析:,
,
,,
,
,
故答案为:100.
13.答案:7
解析:由题意可知,,,
,
,
,
,
,
在和中,
,
,
,,
,
,,
,
故答案为:7.
14.答案:50
解析:如图,在AC上截取,连接BE,
的平分线交BC于点D,
,
,
,
,
.
有最小值,
当BE是点B到直线AC的距离时,,
;
故答案为:50.
15.答案:(1)
(2)2或5
解析:(1),.
为AB边上的高,,
,.
,.
(2)过点E作BC的垂线交直线CD于点F,
,
在和中,
,.
①如图,当点E在射线BC上时,.
点E从点B出发,在直线BC上以的速度移动,
E移动了.
②当点E在射线CB上时,记为,.
点E从点B出发,在直线BC上以的速度移动,
E移动了.
综上所述,当点E移动或时,.
16.答案:(1)全等三角形对应边相等,AF,CD,CD
(2),全等三角形对应角相等,DE,内错角相等,两直线平行.
解析:(1)(已知),
(全等三角形对应边相等),
(等式性质)
即,
;
(2)(已知)
(全等三角形对应角相等)
(内错角相等,两直线平行).
故答案为:(1)全等三角形对应边相等,AF,CD,CD;(2),全等三角形对应角相等,DE,内错角相等,两直线平行.
17.解析:(1)根据题意可得,
河流的宽度为,
故答案为:8;
(2)画出图形如下:
根据题意可得:,,,
,
.
18.答案:(1);
(2),理由见解析;
解析:(1),
,,
,,
,
,
,
故答案为:;
(2).
理由如下:作于F,作交EC的延长线于F,
,
,
,,
,,
,
在和中,
,
,
,
,
,
,,
.
19.解析:①运用“”画图1,作,且使,,连接,
则即为所求;
②运用“”画图2,作线段,分别以R,S为顶点在线段的同侧作,且,交于点P,
则即为所求;
③运用“”画图3,作线段,分别以R,S为圆心,,为半径在的同旁画弧交P点,连接,,则即为所求.
通过作图可得,运用“”作图比较方便.
20.答案:(1)B
(2)C
(3)证明见解析
解析:(1)在和中
,
,
故选:B;
(2)如图:
由(1)知:,
,,
在中,,由三角形三边关系定理得:,
,
故选:C.
(3)延长AD到M,使,连接BM,
是中线,
,
在和中,
,
,
,,
,
,
,
,
,
即.
21.答案:(1),证明见解析
(2),证明见解析
解析:(1),
证明:延长CB到E,使,连接DE,
,,,
,
,
,
,,
,
,
,,
在和中,
,
,
,,
,,
,
,
,
,
在和中,
,
,
,
,
,
(2),
证明:在CB截取,连接DE,
,,,
,
,,
,
,
,
,
,
在和中
,
,
,,
,
,
在和中,
,
,
,
,
.
(测能力)
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.如图,已知,,,则的度数为( )
A.75° B.65° C.40° D.30°
2.下列命题:①同旁内角互补,两直线平行;
②若,则;
③末位数字是5的数,能被5整除;
④对顶角相等.
逆命题是假命题的个数是( )
A.1个 B.2个 C.3个 D.4个
3.数学课上陈老师要求学生利用尺规作图,作一个已知角的角平分线,并保留作图痕迹.学生小敏的作法是:如图,是已知角,以O为圆心,任意长为半径作弧,与、分别交于N、M;再分别以N、M为圆心,大于的长为半径作弧,交于点C;作射线;则射线是的角平分线.小敏作图的依据是( )
A. B. C. D.
4.如果所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店配一块完全一样的玻璃,那么最省事的办法是带( )去.
A.① B.② C.③ D.①和②
5.如图所示,锐角中,D,E分别是,边上的点,,,且,、交于点F,若,则的度数为( )
A.110° B.105° C.100° D.95°
6.如图为6个边长相等的正方形的组合图形,则( )
A. B. C. D.
7.如图,,,,点B,D,E在同一直线上,若,,则的度数是( )
A. B. C. D.
8.如图,OA平分,平分,于点E,于点C,于点D,下列结论错误的是( )
A. B.点O是CD的中点
C. D.
9.如图,,且,且,请按照图中所标注的数据计算图中实线所围成的图形的面积是( )
A.30 B.50 C.60 D.80
10.如图,强强想测量旗杆的高度,旗杆对面有一高为米的大楼,大楼与旗杆相距米(米),在大楼前米的点P处,测得,且,,则旗杆的高为( )
A.8米 B.米 C.米 D.米
二、填空题(每小题4分,共20分)
11.如图,,,与交于点O,,,则的度数为_________.
12.如图,要测量水池宽AB,可从点A出发在地面上画一条线段AC,使,再从点C观测,在BA的延长线上测得一点D,使,这时量得,则水池宽AB是______m.
13.如图所示,中,,.直线l经过点A,过点B作于点E,过点C作于点F.若,,则__________.
14.如图,在锐角中,,的平分线交BC于点D,M,N分别是AD和AB上的动点,当有最小值时,______°.
15.如图,在中,,,,为AB边上的高.
(1)若点E在BC延长线上,点F在DC延长线上,且,则____________(用含的式子表示);
(2)若点E从点B出发,在直线BC上以的速度移动,过点E作BC的垂线交直线CD于点F,当点E运动__________s时,.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,已知,.
(1)求CD的长.
(2)AB与DE平行吗?为什么?
解:(1)(已知),
(___________),
(等式性质)
即________=__________
_________
(2)(已知)
_______(___________)
__________(__________)
17.(8分)如图,有一条河流(假设河流两岸平行,即),由于河水湍急,无法下水,为了测量河的宽度,林师傅给出了以下方法:
①在河岸b上确定点A(如图),利用红外线光束,在河岸a上确定点B,使得与河岸垂直;
②从A点沿河岸向东直走,记为点C(如图),继续向东直走,到达点D;
③从D点沿垂直河岸的方向行走,行走过程中,用红外线光束一直对准B,当点C刚好出现在红外线光束上时,停下,记为点E;
④测得的长为.
(1)根据上述方法,河流的宽度为______m;
(2)请你根据林师傅的方法,利用三角板和刻度尺,在图中画出B,D,E的位置,并结合题意说明林师傅作法的科学性.
18.(10分)已知:,,.
(1)如图1当点D在AB上,________.
(2)如图2猜想与的面积有何关系?请说明理由.(温馨提示:两三角形可以看成是等底的)
19.(10分)已知(如图),用三种不同的方法作,使.你认为哪一种作法比较简便?
20.(12分)【阅读理解】
课外兴趣小组活动时,老师提出了如下问题:
如图1,中,若,,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使,请根据小明的方法思考:
(1)由已知和作图能得到的理由是_____.
A.SSS B.SAS C.AAS D.HL
(2)求得AD的取值范围是______.
A. B. C. D.
【感悟】
解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
【问题解决】
(3)如图2,AD是的中线,BE交AC于E,交AD于F,且.求证:.
21.(12分)在练习课上,慧慧同学遇到了这样一道数学题:如图,把两个全等的直角三角板的斜边重合,组成一个四边形ACBD,,以D为顶点作,交边AC,BC于点M,N,,连接MN.
探究AM,MN,BN三条线段之间的数量关系.
慧慧分析:可先利用旋转,把其中的两条线段“接起来”,再通过证明两三角形全等,从而探究出AM,MN,BN三条线段之间的数量关系.
慧慧编题:在编题演练环节,慧慧编题如下:
如图(1),把两个全等的直角三角板的斜边重合,组成一个四边形,,以D为顶点作,交边AC,BC于点M,N,,连接MN. (1)先猜想AM,MN,BN三条线段之间的数量关系,再证明. (2)绕点D旋转,当M,N分别在CA,BC的延长线上,完成图(2),其余条件不变,直接写出AM,MN,BN三条线段之间的数量关系.
请你解答:请对慧慧同学所编制的问题进行解答.
答案以及解析
1.答案:B
解析:,
,,
,故选B.
2.答案:C
解析:①同旁内角互补,两直线平行的逆命题是两直线平行,同旁内角互补,是真命题;
②若,则的逆命题是若,则;也可以是所以是假命题;
③末位数字是5的数,能被5整除逆命题是能被5整除的数,末位数字是5;末尾数也可以是0,所以是假命题;
④对顶角相等的逆命题是相等的角是对项角,是假命题;
它们的逆命题是假命题的个数是3个.故选C.
3.答案:D
解析:由作图可知,,
又,
,,
,
平分.
故选:D.
4.答案:C
解析:①仅保留了原三角形的一个角和部分边,不符合任何全等三角形判定方法;②仅保留了原三角形的一部分边,所以该块不行;
③不但保留了原三角形的两个角还保留了其中一个边,所以符合判定,所以应该拿这块去.
故选:C.
5.答案:A
解析:设,
,,
,,,
,,
,
,,
,即,则,
,
.
故选:A.
6.答案:B
解析:在和中,
,
,
,
,
,
,
,
故选B.
7.答案:C
解析:,
,
,
,,
,,
,,
,,
.
故选:C.
8.答案:D
解析:平分,平分,,,,故选项C不合题意.在和中,,,,.同理可得,,,,点O是CD的中点,故选项A,B不合题意.选D.
9.答案:B
解析:,,
,
在和中,
,,
同理,
,,,,
梯形DEFH的面积,
,,
图中实线所围成的图形的面积,
故选B.
10.答案:B
解析:由题意得,,,,
,
,
,,
,
,
,
,
,
在和中,
,
,
,
故选:B.
11.答案:
解析:,,,
,,
,
,,,,
,
,
.
故答案为:
12.答案:100
解析:,
,
,,
,
,
故答案为:100.
13.答案:7
解析:由题意可知,,,
,
,
,
,
,
在和中,
,
,
,,
,
,,
,
故答案为:7.
14.答案:50
解析:如图,在AC上截取,连接BE,
的平分线交BC于点D,
,
,
,
,
.
有最小值,
当BE是点B到直线AC的距离时,,
;
故答案为:50.
15.答案:(1)
(2)2或5
解析:(1),.
为AB边上的高,,
,.
,.
(2)过点E作BC的垂线交直线CD于点F,
,
在和中,
,.
①如图,当点E在射线BC上时,.
点E从点B出发,在直线BC上以的速度移动,
E移动了.
②当点E在射线CB上时,记为,.
点E从点B出发,在直线BC上以的速度移动,
E移动了.
综上所述,当点E移动或时,.
16.答案:(1)全等三角形对应边相等,AF,CD,CD
(2),全等三角形对应角相等,DE,内错角相等,两直线平行.
解析:(1)(已知),
(全等三角形对应边相等),
(等式性质)
即,
;
(2)(已知)
(全等三角形对应角相等)
(内错角相等,两直线平行).
故答案为:(1)全等三角形对应边相等,AF,CD,CD;(2),全等三角形对应角相等,DE,内错角相等,两直线平行.
17.解析:(1)根据题意可得,
河流的宽度为,
故答案为:8;
(2)画出图形如下:
根据题意可得:,,,
,
.
18.答案:(1);
(2),理由见解析;
解析:(1),
,,
,,
,
,
,
故答案为:;
(2).
理由如下:作于F,作交EC的延长线于F,
,
,
,,
,,
,
在和中,
,
,
,
,
,
,,
.
19.解析:①运用“”画图1,作,且使,,连接,
则即为所求;
②运用“”画图2,作线段,分别以R,S为顶点在线段的同侧作,且,交于点P,
则即为所求;
③运用“”画图3,作线段,分别以R,S为圆心,,为半径在的同旁画弧交P点,连接,,则即为所求.
通过作图可得,运用“”作图比较方便.
20.答案:(1)B
(2)C
(3)证明见解析
解析:(1)在和中
,
,
故选:B;
(2)如图:
由(1)知:,
,,
在中,,由三角形三边关系定理得:,
,
故选:C.
(3)延长AD到M,使,连接BM,
是中线,
,
在和中,
,
,
,,
,
,
,
,
,
即.
21.答案:(1),证明见解析
(2),证明见解析
解析:(1),
证明:延长CB到E,使,连接DE,
,,,
,
,
,
,,
,
,
,,
在和中,
,
,
,,
,,
,
,
,
,
在和中,
,
,
,
,
,
(2),
证明:在CB截取,连接DE,
,,,
,
,,
,
,
,
,
,
在和中
,
,
,,
,
,
在和中,
,
,
,
,
.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
