第五章 圆培优专题 圆心角、弧、弦之间关系的应用(含答案)
文档属性
| 名称 | 第五章 圆培优专题 圆心角、弧、弦之间关系的应用(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 12.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-21 21:29:12 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第五章 圆
培优专题 圆心角、弧、弦之间关系的应用
应用一:利用圆心角、弧、弦之间关系求角的度数
1.如图,点A,B,C,D 在⊙O上,∠AOC=140°,点 B 是. 的中点,则∠D 的度数是( )
A.70° B.55° C.35.5° D.35°
2.如图,AB 和 CD 是⊙O 的两条直径,弦DE∥AB,若弧 DE 的度数为 40°,则 ∠BOC=( )
A.110° B.80° C.40° D.70°
3.如图,已知 BD 是⊙O 的直径,点 A,C 在⊙O 上, ∠AOB=60°,则∠COD的度数是___________度.
4.[一题多辨](1)如图①,在⊙O中, ∠A=40°,则∠B=__________.
(2)如图②,已知AB是⊙O 的直径,PA=PB,∠P =60°,则 所对的 圆心角等于________.
应用二:利用圆心角、弧、弦之间关系求弧的度数
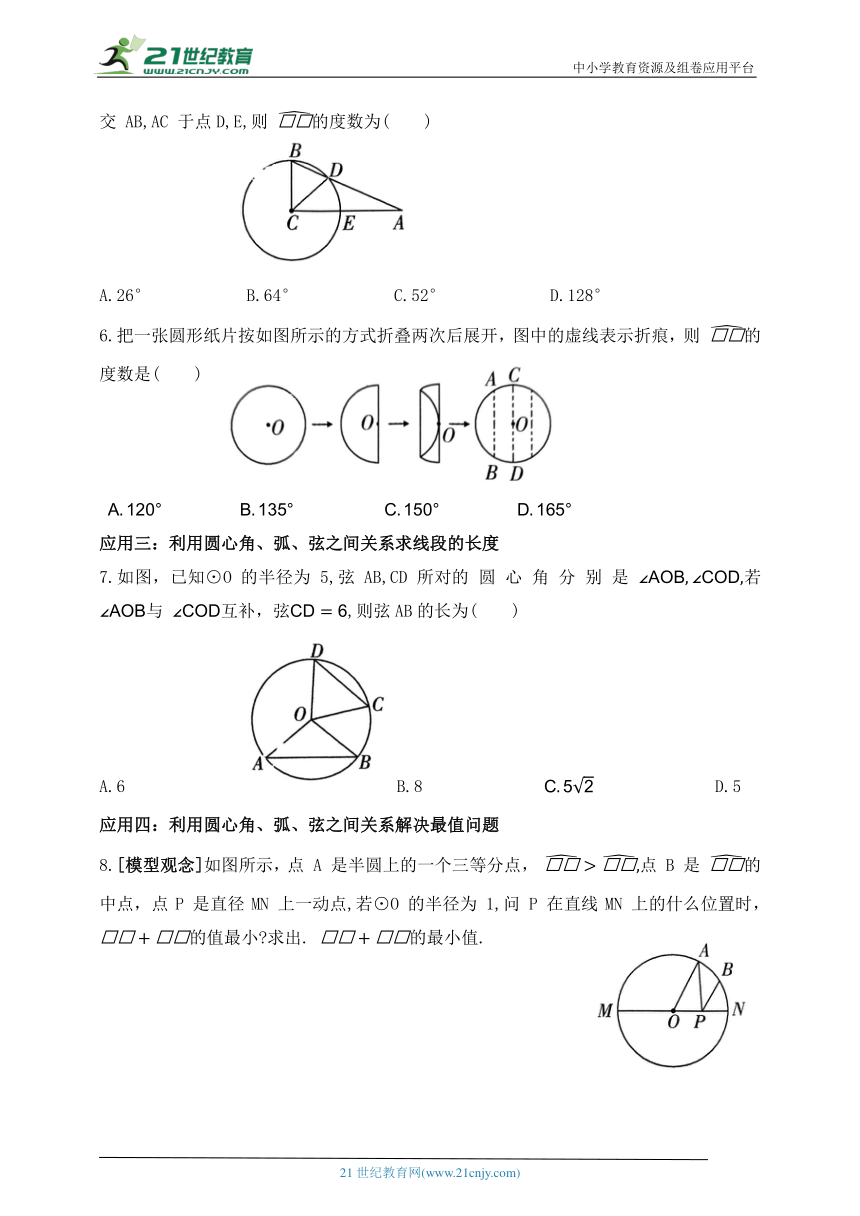
5. 如 图, 在 Rt△ABC 中,∠ACB=90°,∠A =26°,以点 C 为圆心,BC 为半径的圆分别交 AB,AC 于点D,E,则 的度数为( )
A.26° B.64° C.52° D.128°
6.把一张圆形纸片按如图所示的方式折叠两次后展开,图中的虚线表示折痕,则 的度数是( )
应用三:利用圆心角、弧、弦之间关系求线段的长度
7.如图,已知⊙O的半径为 5,弦AB,CD所对的 圆 心 角 分 别 是 若 与 互补,弦,则弦AB的长为( )
A.6 B.8 D.5
应用四:利用圆心角、弧、弦之间关系解决最值问题
8.[模型观念]如图所示,点 A 是半圆上的一个三等分点, 点 B 是 的中点,点P 是直径MN 上一动点,若⊙O 的半径为 1,问 P 在直线MN 上的什么位置时, 的值最小 求出. 的最小值.
参考答案
1. D 2. A 3.120 5. C 6. C 7. B
8.解:如图,作点 B 关于直线MN 的对称点. 则点 必在⊙O上,且 连接OB, 由已知得 60°.
∵ 点 B 是 的 中 点,
连接 交MN于 点则点即为所求的点.
连接 此时
即 的最小值为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
培优专题 圆心角、弧、弦之间关系的应用
应用一:利用圆心角、弧、弦之间关系求角的度数
1.如图,点A,B,C,D 在⊙O上,∠AOC=140°,点 B 是. 的中点,则∠D 的度数是( )
A.70° B.55° C.35.5° D.35°
2.如图,AB 和 CD 是⊙O 的两条直径,弦DE∥AB,若弧 DE 的度数为 40°,则 ∠BOC=( )
A.110° B.80° C.40° D.70°
3.如图,已知 BD 是⊙O 的直径,点 A,C 在⊙O 上, ∠AOB=60°,则∠COD的度数是___________度.
4.[一题多辨](1)如图①,在⊙O中, ∠A=40°,则∠B=__________.
(2)如图②,已知AB是⊙O 的直径,PA=PB,∠P =60°,则 所对的 圆心角等于________.
应用二:利用圆心角、弧、弦之间关系求弧的度数
5. 如 图, 在 Rt△ABC 中,∠ACB=90°,∠A =26°,以点 C 为圆心,BC 为半径的圆分别交 AB,AC 于点D,E,则 的度数为( )
A.26° B.64° C.52° D.128°
6.把一张圆形纸片按如图所示的方式折叠两次后展开,图中的虚线表示折痕,则 的度数是( )
应用三:利用圆心角、弧、弦之间关系求线段的长度
7.如图,已知⊙O的半径为 5,弦AB,CD所对的 圆 心 角 分 别 是 若 与 互补,弦,则弦AB的长为( )
A.6 B.8 D.5
应用四:利用圆心角、弧、弦之间关系解决最值问题
8.[模型观念]如图所示,点 A 是半圆上的一个三等分点, 点 B 是 的中点,点P 是直径MN 上一动点,若⊙O 的半径为 1,问 P 在直线MN 上的什么位置时, 的值最小 求出. 的最小值.
参考答案
1. D 2. A 3.120 5. C 6. C 7. B
8.解:如图,作点 B 关于直线MN 的对称点. 则点 必在⊙O上,且 连接OB, 由已知得 60°.
∵ 点 B 是 的 中 点,
连接 交MN于 点则点即为所求的点.
连接 此时
即 的最小值为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
