北京市2023-2024学年高三上学期期中考试数学试题(PDF版含答案)
文档属性
| 名称 | 北京市2023-2024学年高三上学期期中考试数学试题(PDF版含答案) |

|
|
| 格式 | |||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-21 00:00:00 | ||
图片预览



文档简介
2023-2024 学年度第一学期
期中考试
高三年级 数学学科
本试卷共 6 页,共 150 分.考试时长 120 分钟.考生务必将答案答在答题卡上,在试卷上
作答无效.
一、选择题(每题 4 分,共 40 分)
2
1. 已知集合 A x x x 6 0 , B y y | x | 1 ,则 A B ( )
A. [1,2] B. [1,3] C. [0,2] D. [0,3]
2. 下列命题中,正确的是 ( )
A.1 2i的虚部是 2 B. |1 2i | 5
C.1 2i的共轭复数是 1 2i D.1 2i在复平面内对应的点在第二象限
3.已知点 P(6, 8) 是角 终边上一点,则 sin( ) ( )
2
3 3 4 4
A. B. C. D.
5 5 5 5
4. 已知 l ,m 表示两条不同的直线, 表示平面,则下列说法正确的是 ( )
A.若 l / /m ,m ,则 l / / B.若 l / / ,m ,则 l / /m
C.若 l m ,m ,则 l D. 若 l ,m ,则 l m
5.在△ ABC 中,点 D在边 AB上,BD 2DA.记CA m,CD n .则CB ( )
A. 3m 2n B. 2m 3n C. 3m 2n D. 2m 3n
2
6.函数 f (x) 3sin 2x 2cos x在区间[0, ]上的最大值为 ( )
2
1
A. B. 3 1 C.1 D. 3
2
2
7. 在数列{an}中,已知an n n,n N
* ,则“ a1 a2 ”是“{a ( )n}是单调递增数列”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
1
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
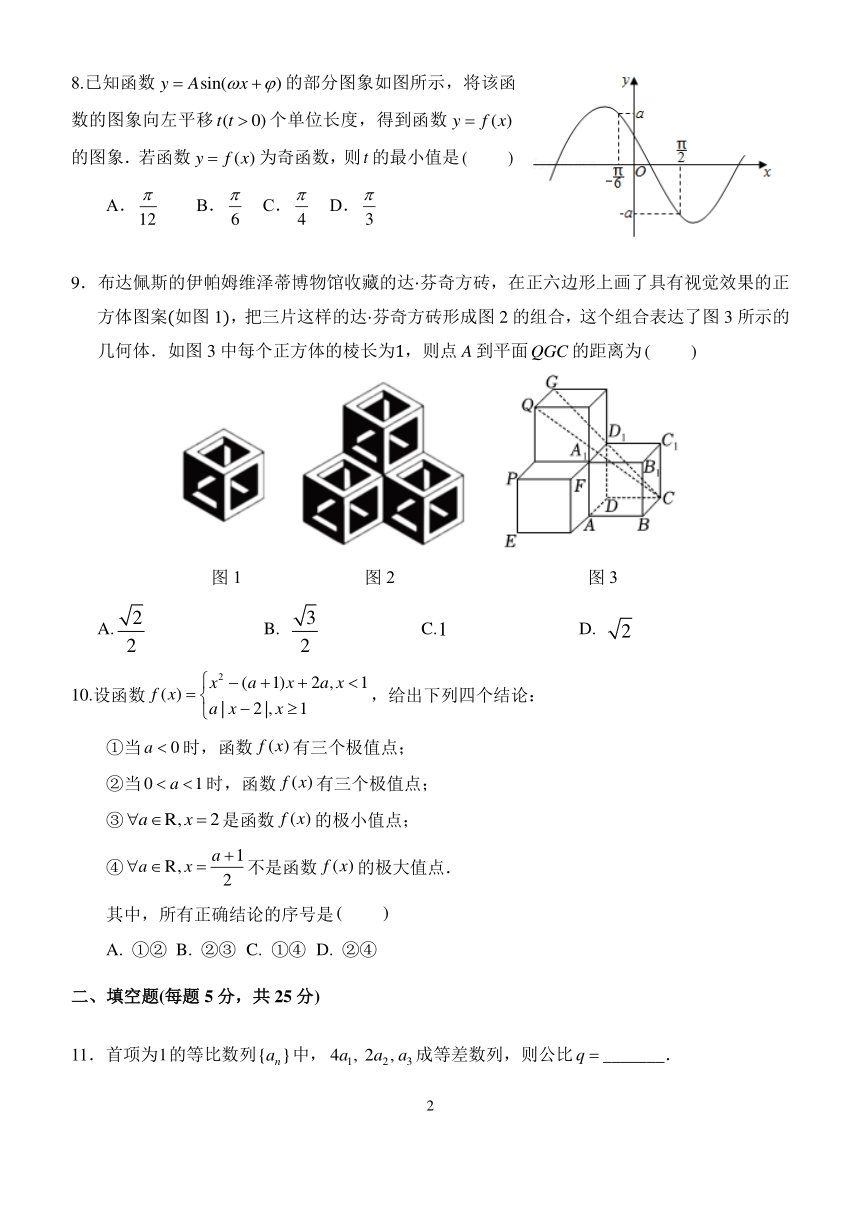
8.已知函数 y Asin( x ) 的部分图象如图所示,将该函
数的图象向左平移 t(t 0)个单位长度,得到函数 y f (x)
的图象.若函数 y f (x) 为奇函数,则 t 的最小值是 ( )
A. B. C. D.
12 6 4 3
9.布达佩斯的伊帕姆维泽蒂博物馆收藏的达 芬奇方砖,在正六边形上画了具有视觉效果的正
方体图案(如图 1),把三片这样的达 芬奇方砖形成图 2 的组合,这个组合表达了图 3 所示的
几何体.如图 3 中每个正方体的棱长为1,则点 A 到平面QGC 的距离为 ( )
图 1 图 2 图 3
2 3
A. B. C.1 D. 2
2 2
x2 (a 1)x 2a, x 1
10.设函数 f (x) ,给出下列四个结论:
a | x 2 |, x 1
①当 a 0 时,函数 f (x) 有三个极值点;
②当 0 a 1时,函数 f (x) 有三个极值点;
③ a R, x 2是函数 f (x)的极小值点;
a 1
④ a R, x 不是函数 f (x) 的极大值点.
2
其中,所有正确结论的序号是 ( )
A. ①② B. ②③ C. ①④ D. ②④
二、填空题(每题 5 分,共 25 分)
11.首项为1的等比数列{an}中, 4a1, 2a2 , a3 成等差数列,则公比 q _______.
2
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
x 1
12.若函数 f (x) 2 a ( )
x
为偶函数,则a ________, f (x) 的最小值为_______.
2
4 3
13.已知正四棱锥 S ABCD,底面边长为 2 ,体积为 ,则这个四棱锥的侧棱长为_______.
3
*
14.已知数列 an 满足a1 1,a2n n 1,a2n 1 a2n a2n 1,n N .则集合{m | am 20}
中元素的个数为________.
1 5
15.已知 e1,e2 是空间单位向量, e1 e2 ,若空间向量b 满足b e1 2,b e2 ,且对于
2 2
任意 x, y R , b (xe1 ye2 ) b (x0e1 y0e2 ) 1(x0 , y0 R) ,则 x0 y0 ,
b .
三、解答题(本大题共 6 小题,共 85 分. 解答应写出文字说明,证明过程或演算步骤)
16.(13 分) △ ABC 中,b2 c2 a2 3bc .
(Ⅰ)求 A的大小;
(Ⅱ)以下三组条件中恰有一组条件使得三角形存在且唯一确定,请选出该组条件,
并求△ ABC 的面积.
2
条件①: sin在B ,b 2 ; 22 2条件②:cos B , a 2 ; 3
条件③:a 1,b 2 .
注:条件选择错误,第(2)问得 0 分.
3
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
17. (14 分)如图,已知平面PAB 平面 ABCD,四边形 ABCD是矩形,PA AB,点E ,
F 分别是BC , PB 的中点.
(Ⅰ)若点M 为线段 AD 中点,求证:PM ∥平面 AEF ;
(Ⅱ)求证: AF 平面PBC .
18. (15 分)已知函数 f (x) x ln x .
(Ⅰ)求曲线 y f (x) 在点 (1, f (1))处的切线方程;
(Ⅱ)求 f (x) 的单调区间;
1
(Ⅲ)若对于任意 x [ ,e],都有 f (x) ax 1,求实数a 的取值范围.
e
4
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
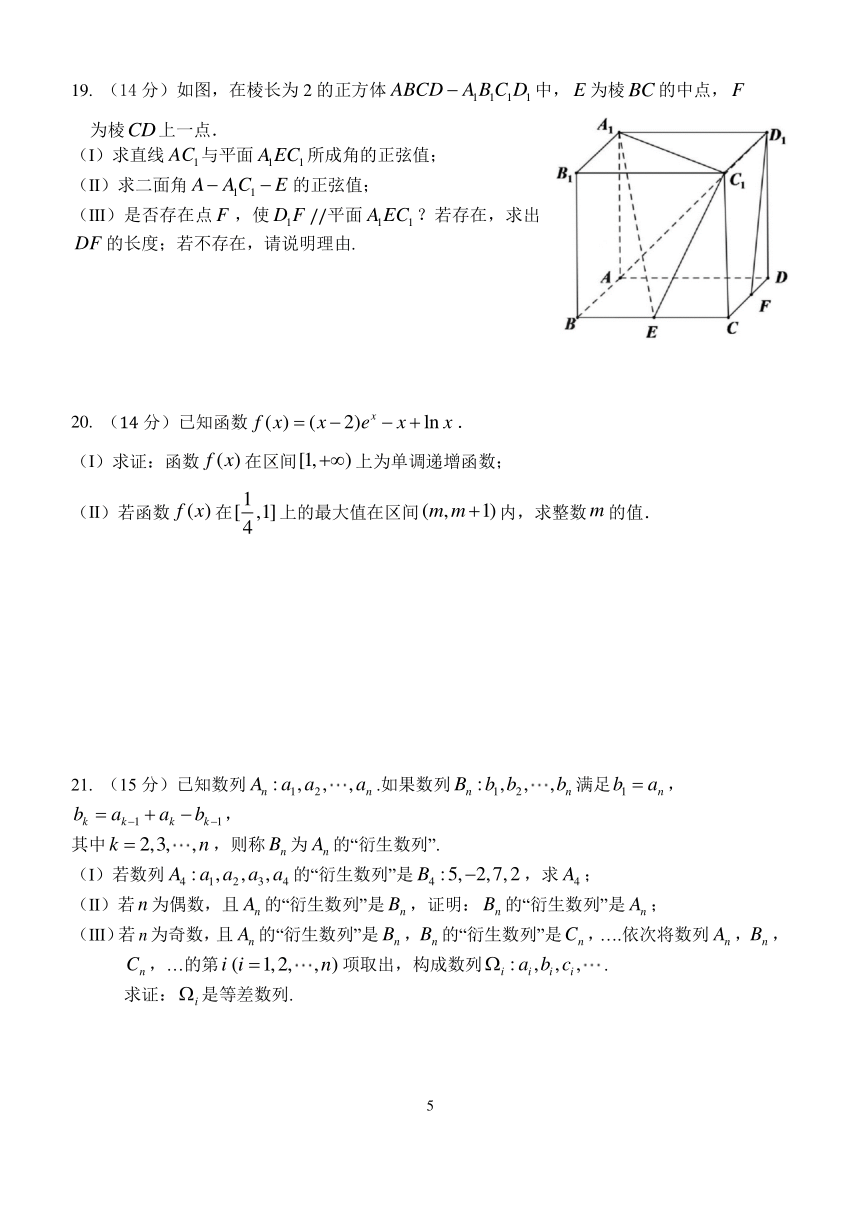
19. (14 分)如图,在棱长为 2 的正方体 ABCD A1B1C1D1 中,E 为棱BC 的中点,F
为棱CD上一点.
(Ⅰ)求直线 AC1与平面 A1EC1所成角的正弦值;
(Ⅱ)求二面角 A A1C1 E 的正弦值;
(Ⅲ)是否存在点 F ,使 D1F //平面 A1EC1 ?若存在,求出
DF 的长度;若不存在,请说明理由.
20. (14 分)已知函数 f (x) (x 2)ex x ln x .
(Ⅰ)求证:函数 f (x) 在区间[1, ) 上为单调递增函数;
1
(Ⅱ)若函数 f (x) 在[ ,1]上的最大值在区间 (m,m 1)内,求整数m 的值.
4
21. (15 分)已知数列 An : a1,a2 , ,an .如果数列Bn :b1,b2 , ,bn 满足b1 an ,
bk ak 1 ak bk 1,
其中 k 2,3, ,n,则称Bn 为 An 的“衍生数列”.
(Ⅰ)若数列 A4 : a1,a2 ,a3 ,a4 的“衍生数列”是 B4 : 5, 2,7, 2,求 A4 ;
(Ⅱ)若n 为偶数,且 An 的“衍生数列”是Bn ,证明:Bn 的“衍生数列”是 An ;
(Ⅲ)若 n为奇数,且 An 的“衍生数列”是Bn ,Bn 的“衍生数列”是Cn ,….依次将数列 An ,Bn ,
Cn ,…的第 i (i 1,2, ,n) 项取出,构成数列 i : ai ,bi ,ci , .
求证: i 是等差数列.
5
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
(此页为答题纸,请勿在此作答)
6
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
【参考答案】
一、选择题:BBADB CCBAD
二、填空题
11. 2
12. -1,2
13. 6
14.24
15.3,2 2
16.(1)由余弦定理a2 b2 c2 2bccos A,又b2 c2 a2 3bc ,可得
3
2bc cos A 3bc ,所以cos A ,又因为 A 0, ,所以 A
2 6
(2)选择条件②
2 2
由(1)知, A ,根据条件②中 cos B ,B 0, ,所以 B 也是唯一确定的,
6 3
从而可得 C也是唯一确定的,再由a 2 ,代入正弦定理计算可得边b,c也是唯一确定
的,故选择条件②.
2 2 1
因为cos B , B 0, ,所以sin B .
3 3
a b
由正弦定理 ,
sin A sin B
1
2
sin B 3 2 2
可得b a ,
sin A 1 3
2
1 2 2 3 1 2 2 3
所以sin C sin A B sin Acos B cos Asin B
2 3 2 3 6
1 2 2 3
所以三角形面积 S absin C
2 9
7
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
17.(Ⅰ)证明:连结BM 交 AE 于 N ,连结PM ,FN .
因为四边形 ABCD是矩形,
所以 AD//BC,且 AD=BC ,
又M , E 分别为 AD , A 的中点,
所以四边形 AMEB 是平行四边形,
所以 N 为BM 的中点,
又因为M 是 PB 的中点,
所以PM ∥FN ,
因为PM 平面 AEF , NF 平面 AEF ,
所以PM ∥平面 AEF .
(Ⅱ)证明:
在矩形ABCD中, BC AB
BC AB
面PAB 面ABCD
面PAB 面ABCD AB
BC 面ABCD
BC 面PAB
因为 AF 平面PAB,
所以BC AF .
因为PA AB,点M 是PB 的中点,
所以PB AF
又因为BC PB B,
所以 AF 平面PBC .
18.解:(Ⅰ)因为函数 ( ) = ,
′ 1
所以 ( ) = + = + 1,
′(1) = 1 + 1 = 1.
又因为 (1) = 0,
所以曲线 = ( )在点(1, (1))处的切线方程为 = 1.
8
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
(Ⅱ)函数 ( ) = 定义域为(0,+∞),
由(Ⅰ)可知, ′( ) = + 1.
1
令 ′( ) = 0,解得 = .
( )与 ′( )在区间(0,+∞)上的情况如下:
1 1 1
(0, ) ( ,+∞)
′( ) 0 +
( ) ↓ 极小值 ↑
1 1
故 ( )的增区间为( , +∞),减区间为(0, ).
1 1
(Ⅲ)当 时,“ ( ) ≤ 1”等价于“ ≥ ln + ”恒成立,
1 1
令 ( ) = ln + , ∈ [ , ],
1 1 1 1
′( ) = 2 = 2 , ∈ [ , ].
1 1
当 ∈ [ , 1)时, ( ) < 0,所以 ( )在区间[ , 1)单调递减.
当 ∈ (1, ]时, ( ) > 0,所以 ( )在区间(1, ]单调递增.
1 1
而 ( ) = ln + = 1 > 1.5, ( ) = 1 + < 1.5,
1 1
所以 ( )在区间[ , ]上的最大值为 ( ) = 1.
1
所以当 ≥ 1时,对于任意 ∈ [ , ],都有 ( ) ≤ 1.
19.(1) 以 为原点, , , 1分别为 , , 轴,建立如
图空间直角坐标系,
则 (0,0,0), 1(0,0,2), (2,0,0), (2,2,0),
(0,2,0), 1(2,2,2), 1(0,2,2),E(2,1,0)
AC1 (2,2,2), A1C (2,2,0), EC1 (0,1,2) 1
设平面 A1C1E 的一个法向量为m (x, y, z)
m A1C1 0
不妨设 = 2,则 = 2, = 1,
m EC1 0
m ( 2,2, 1)
设直线 1与平面 1 1所成角为 ,
9
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
则 m AC 2 3sin | cos m, AC | 1 . 1
m , AC 3 2 3 91
→
(2)由正方体可得,平面 1 1的一个法向量为 = (2, 2,0),
DB m 8 2 2
则 cos DB,m .
DB m 3 2 2 3
因为二面角 1 1 为锐二面角,
→ → 1
所以二面角 1 1 的正弦值为 √1 cos
2 , = .
3
(3)存在,设 F 点的坐标为(t,2,0),所以 1 = ( , 0,2)
→
平面 1 1的一个法向量为 = ( 2,2, 1),
→
因为 1 ⊥ ,所以 1 = 0,t = 1
因为 1 平面 1 1,所以 1 //平面 1 1.此时 = 1
20.解:(1)
1 1
∈ [1,+∞), ′( ) = + ( 2) 1 + = ( 1) ( )
x
1 1
当 ≥ 1时x 1 ≥ 0,ex ≥ , ≤ 1, > ∴ ′( ) ≥ 0, ( )单调递增
1 1
(2) ′( ) = ( 1) 1 + = ( 1)( ).
1 1 1
令 ( ) = ,则 ′( ) = + > 0,所以 ( )在[ , 1]上单调递增,
2 4
因为 1
1
( ) = 2 2 < 0, (1) = 1 > 0,
2
1 1
所以存在 0 ∈ ( , 1),使得 ( 0) = 0,即
0 = ,即ln 0 = , 2 00
1
故当 ∈ [ , 0)时, ( ) < 0,当 ∈ ( 0, 1]时, ( ) > 0, 4
1 1
又当 ∈ [ , 1]时, 1 ≤ 0(等号仅在 = 1时成立),所以当 ∈ [ , )时, ′( ) > 0,
4 4 0
当 ∈ ( 0, 1]时, ′( ) ≤ 0(等号仅在 = 1时成立),
1
所以 ( )在[ ,
4 0
)上单调递增,在( 0, 1]上单调递减,
1 2
则 ( )max = ( 0) = ( 0 2)
0 0 + ln 0 = ( 0 2) 0 0 = 1 2 , 0 00
2 1
令 2 2(1
2) 1
( ) = 1 2 , ∈ ( , 1),则 ′( ) = 2 2 = 2 > 0( ∈ ( , 1)), 2 2
10
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
1 1
所以 ( )在( , 1)上单调递增,则 ( ) > ( ) = 4, ( ) < (1) = 3,
2 2
所以 4 < ( ) < 3,所以 = 4.
21.(Ⅰ)解: . ………3A4 : 2,1, 4,5
分
(Ⅱ)证法一:
证明:由已知,b1 a1 (a1 an ) ,b2 a1 a2 b1 a2 (a1 an ) .
因此,猜想b a ( 1)i (a a ) . ………………4 分 i i 1 n
① 当 i 1时,b1 a1 (a1 an ) ,猜想成立;
② k 假设 i k (k *N ) 时,bk ak ( 1) (a1 an ) .
当 i k 1时,bk 1 ak ak 1 bk
ak ak 1 [ak ( 1)
k (a 1 an )]
ak ak 1 ak ( 1)
k (a1 an )
a ( 1)k 1(a a ) k 1 1 n
故当 i k 1时猜想也成立.
由 ①、② 可知,对于任意正整数 i ,有bi ai ( 1)
i (a a ) . ………………7 分 1 n
设数列Bn 的“衍生数列”为Cn ,则由以上结论可知
c b ( 1)i (b b ) a ( 1)i (a a ) ( 1)ii i n i n (b ,其中1 1 1 bn) i 1,2,3, ,n .
由于n 为偶数,所以bn an ( 1)
n (a1 an ) a1 ,
所以 ci ai ( 1)
i (a1 an ) ( 1)
i (an a1) ai ,其中 i 1,2,3, ,n .
因此,数列Cn 即是数列 An . ………………9 分
证法二:
因为 b1 an ,
b1 b2 a1 a2 ,
b2 b3 a2 a3 ,
……
bn 1 bn an 1 an ,
n
由于n 为偶数,将上述 n 个等式中的第2,4,6, ,n这 个式子都乘以 1,相加得
2
b1 (b1 b2 ) (b2 b3) (bn 1 bn ) an (a1 a2 ) (a2 a3) (an 1 an )
即 bn a1,bn a1 . ………………7 分
由于a1 bn , ai bi 1 bi ai 1 (i 2,3, ,n),
根据“衍生数列”的定义知,数列 An 是 Bn 的“衍生数列”. ………………9 分
(Ⅲ)证法一:
证明:设数列 X n , Yn , Zn 中后者是前者的“衍生数列”.欲证 i 成等差数列,只需证明
x , y , z 成等差数列,即只要证明2yi xi z (i 1,2,3, ,n)i i i i 即可. ……10 分
11
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
由(Ⅱ)中结论可知 yi xi ( 1)
i (x x ), 1 n
zi y ( 1)
i (y y i 1 n )
xi ( 1)
i (x1 xn ) ( 1)
i (y1 yn )
xi ( 1)
i (x x i n 1 n ) ( 1) [xn xn ( 1) (x1 xn)]
xi ( 1)
i (x1 xn) ( 1)
i (x x ) 1 n
xi 2( 1)
i (x , 1 xn )
所以, x z 2x 2( 1)i (x x ) 2y ,即 xi , yi , zi 成等差数列, i i i 1 n i
所以 i 是等差数列. ………………13 分
证法二:
因为 bi ai 1 ai bi 1 (i 2,3,4, ,n) ,
所以 bi ai (bi 1 ai 1) (i 2,3,4, ,n) .
所以欲证 i 成等差数列,只需证明 1 成等差数列即可. ………………10 分
对于数列 An 及其“衍生数列” Bn ,
因为 b1 an ,
b1 b2 a1 a2 ,
b2 b3 a2 a3 ,
……
bn 1 bn an 1 an ,
n 1
由于n 为奇数,将上述 n 个等式中的第2,4,6, ,n 1这 个式子都乘以 1,
2
相加得
b1 (b1 b2 ) (b2 b3) (bn 1 bn ) an (a1 a2 ) (a2 a3) (an 1 an )
即bn an a1 an 2an a1 .
设数列Bn 的“衍生数列”为Cn ,
因为 b1 an ,c1 bn 2an a1 ,
所以 2b1 a1 c1, 即a1,b1,c1成等差数列.
同理可证,b1,c1,d1;c1,d1,e1, 也成等差数列.
即 1 是等差数列.
所以 i 成等差数列. ………………13 分
12
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
期中考试
高三年级 数学学科
本试卷共 6 页,共 150 分.考试时长 120 分钟.考生务必将答案答在答题卡上,在试卷上
作答无效.
一、选择题(每题 4 分,共 40 分)
2
1. 已知集合 A x x x 6 0 , B y y | x | 1 ,则 A B ( )
A. [1,2] B. [1,3] C. [0,2] D. [0,3]
2. 下列命题中,正确的是 ( )
A.1 2i的虚部是 2 B. |1 2i | 5
C.1 2i的共轭复数是 1 2i D.1 2i在复平面内对应的点在第二象限
3.已知点 P(6, 8) 是角 终边上一点,则 sin( ) ( )
2
3 3 4 4
A. B. C. D.
5 5 5 5
4. 已知 l ,m 表示两条不同的直线, 表示平面,则下列说法正确的是 ( )
A.若 l / /m ,m ,则 l / / B.若 l / / ,m ,则 l / /m
C.若 l m ,m ,则 l D. 若 l ,m ,则 l m
5.在△ ABC 中,点 D在边 AB上,BD 2DA.记CA m,CD n .则CB ( )
A. 3m 2n B. 2m 3n C. 3m 2n D. 2m 3n
2
6.函数 f (x) 3sin 2x 2cos x在区间[0, ]上的最大值为 ( )
2
1
A. B. 3 1 C.1 D. 3
2
2
7. 在数列{an}中,已知an n n,n N
* ,则“ a1 a2 ”是“{a ( )n}是单调递增数列”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
1
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
8.已知函数 y Asin( x ) 的部分图象如图所示,将该函
数的图象向左平移 t(t 0)个单位长度,得到函数 y f (x)
的图象.若函数 y f (x) 为奇函数,则 t 的最小值是 ( )
A. B. C. D.
12 6 4 3
9.布达佩斯的伊帕姆维泽蒂博物馆收藏的达 芬奇方砖,在正六边形上画了具有视觉效果的正
方体图案(如图 1),把三片这样的达 芬奇方砖形成图 2 的组合,这个组合表达了图 3 所示的
几何体.如图 3 中每个正方体的棱长为1,则点 A 到平面QGC 的距离为 ( )
图 1 图 2 图 3
2 3
A. B. C.1 D. 2
2 2
x2 (a 1)x 2a, x 1
10.设函数 f (x) ,给出下列四个结论:
a | x 2 |, x 1
①当 a 0 时,函数 f (x) 有三个极值点;
②当 0 a 1时,函数 f (x) 有三个极值点;
③ a R, x 2是函数 f (x)的极小值点;
a 1
④ a R, x 不是函数 f (x) 的极大值点.
2
其中,所有正确结论的序号是 ( )
A. ①② B. ②③ C. ①④ D. ②④
二、填空题(每题 5 分,共 25 分)
11.首项为1的等比数列{an}中, 4a1, 2a2 , a3 成等差数列,则公比 q _______.
2
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
x 1
12.若函数 f (x) 2 a ( )
x
为偶函数,则a ________, f (x) 的最小值为_______.
2
4 3
13.已知正四棱锥 S ABCD,底面边长为 2 ,体积为 ,则这个四棱锥的侧棱长为_______.
3
*
14.已知数列 an 满足a1 1,a2n n 1,a2n 1 a2n a2n 1,n N .则集合{m | am 20}
中元素的个数为________.
1 5
15.已知 e1,e2 是空间单位向量, e1 e2 ,若空间向量b 满足b e1 2,b e2 ,且对于
2 2
任意 x, y R , b (xe1 ye2 ) b (x0e1 y0e2 ) 1(x0 , y0 R) ,则 x0 y0 ,
b .
三、解答题(本大题共 6 小题,共 85 分. 解答应写出文字说明,证明过程或演算步骤)
16.(13 分) △ ABC 中,b2 c2 a2 3bc .
(Ⅰ)求 A的大小;
(Ⅱ)以下三组条件中恰有一组条件使得三角形存在且唯一确定,请选出该组条件,
并求△ ABC 的面积.
2
条件①: sin在B ,b 2 ; 22 2条件②:cos B , a 2 ; 3
条件③:a 1,b 2 .
注:条件选择错误,第(2)问得 0 分.
3
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
17. (14 分)如图,已知平面PAB 平面 ABCD,四边形 ABCD是矩形,PA AB,点E ,
F 分别是BC , PB 的中点.
(Ⅰ)若点M 为线段 AD 中点,求证:PM ∥平面 AEF ;
(Ⅱ)求证: AF 平面PBC .
18. (15 分)已知函数 f (x) x ln x .
(Ⅰ)求曲线 y f (x) 在点 (1, f (1))处的切线方程;
(Ⅱ)求 f (x) 的单调区间;
1
(Ⅲ)若对于任意 x [ ,e],都有 f (x) ax 1,求实数a 的取值范围.
e
4
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
19. (14 分)如图,在棱长为 2 的正方体 ABCD A1B1C1D1 中,E 为棱BC 的中点,F
为棱CD上一点.
(Ⅰ)求直线 AC1与平面 A1EC1所成角的正弦值;
(Ⅱ)求二面角 A A1C1 E 的正弦值;
(Ⅲ)是否存在点 F ,使 D1F //平面 A1EC1 ?若存在,求出
DF 的长度;若不存在,请说明理由.
20. (14 分)已知函数 f (x) (x 2)ex x ln x .
(Ⅰ)求证:函数 f (x) 在区间[1, ) 上为单调递增函数;
1
(Ⅱ)若函数 f (x) 在[ ,1]上的最大值在区间 (m,m 1)内,求整数m 的值.
4
21. (15 分)已知数列 An : a1,a2 , ,an .如果数列Bn :b1,b2 , ,bn 满足b1 an ,
bk ak 1 ak bk 1,
其中 k 2,3, ,n,则称Bn 为 An 的“衍生数列”.
(Ⅰ)若数列 A4 : a1,a2 ,a3 ,a4 的“衍生数列”是 B4 : 5, 2,7, 2,求 A4 ;
(Ⅱ)若n 为偶数,且 An 的“衍生数列”是Bn ,证明:Bn 的“衍生数列”是 An ;
(Ⅲ)若 n为奇数,且 An 的“衍生数列”是Bn ,Bn 的“衍生数列”是Cn ,….依次将数列 An ,Bn ,
Cn ,…的第 i (i 1,2, ,n) 项取出,构成数列 i : ai ,bi ,ci , .
求证: i 是等差数列.
5
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
(此页为答题纸,请勿在此作答)
6
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
【参考答案】
一、选择题:BBADB CCBAD
二、填空题
11. 2
12. -1,2
13. 6
14.24
15.3,2 2
16.(1)由余弦定理a2 b2 c2 2bccos A,又b2 c2 a2 3bc ,可得
3
2bc cos A 3bc ,所以cos A ,又因为 A 0, ,所以 A
2 6
(2)选择条件②
2 2
由(1)知, A ,根据条件②中 cos B ,B 0, ,所以 B 也是唯一确定的,
6 3
从而可得 C也是唯一确定的,再由a 2 ,代入正弦定理计算可得边b,c也是唯一确定
的,故选择条件②.
2 2 1
因为cos B , B 0, ,所以sin B .
3 3
a b
由正弦定理 ,
sin A sin B
1
2
sin B 3 2 2
可得b a ,
sin A 1 3
2
1 2 2 3 1 2 2 3
所以sin C sin A B sin Acos B cos Asin B
2 3 2 3 6
1 2 2 3
所以三角形面积 S absin C
2 9
7
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
17.(Ⅰ)证明:连结BM 交 AE 于 N ,连结PM ,FN .
因为四边形 ABCD是矩形,
所以 AD//BC,且 AD=BC ,
又M , E 分别为 AD , A 的中点,
所以四边形 AMEB 是平行四边形,
所以 N 为BM 的中点,
又因为M 是 PB 的中点,
所以PM ∥FN ,
因为PM 平面 AEF , NF 平面 AEF ,
所以PM ∥平面 AEF .
(Ⅱ)证明:
在矩形ABCD中, BC AB
BC AB
面PAB 面ABCD
面PAB 面ABCD AB
BC 面ABCD
BC 面PAB
因为 AF 平面PAB,
所以BC AF .
因为PA AB,点M 是PB 的中点,
所以PB AF
又因为BC PB B,
所以 AF 平面PBC .
18.解:(Ⅰ)因为函数 ( ) = ,
′ 1
所以 ( ) = + = + 1,
′(1) = 1 + 1 = 1.
又因为 (1) = 0,
所以曲线 = ( )在点(1, (1))处的切线方程为 = 1.
8
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
(Ⅱ)函数 ( ) = 定义域为(0,+∞),
由(Ⅰ)可知, ′( ) = + 1.
1
令 ′( ) = 0,解得 = .
( )与 ′( )在区间(0,+∞)上的情况如下:
1 1 1
(0, ) ( ,+∞)
′( ) 0 +
( ) ↓ 极小值 ↑
1 1
故 ( )的增区间为( , +∞),减区间为(0, ).
1 1
(Ⅲ)当 时,“ ( ) ≤ 1”等价于“ ≥ ln + ”恒成立,
1 1
令 ( ) = ln + , ∈ [ , ],
1 1 1 1
′( ) = 2 = 2 , ∈ [ , ].
1 1
当 ∈ [ , 1)时, ( ) < 0,所以 ( )在区间[ , 1)单调递减.
当 ∈ (1, ]时, ( ) > 0,所以 ( )在区间(1, ]单调递增.
1 1
而 ( ) = ln + = 1 > 1.5, ( ) = 1 + < 1.5,
1 1
所以 ( )在区间[ , ]上的最大值为 ( ) = 1.
1
所以当 ≥ 1时,对于任意 ∈ [ , ],都有 ( ) ≤ 1.
19.(1) 以 为原点, , , 1分别为 , , 轴,建立如
图空间直角坐标系,
则 (0,0,0), 1(0,0,2), (2,0,0), (2,2,0),
(0,2,0), 1(2,2,2), 1(0,2,2),E(2,1,0)
AC1 (2,2,2), A1C (2,2,0), EC1 (0,1,2) 1
设平面 A1C1E 的一个法向量为m (x, y, z)
m A1C1 0
不妨设 = 2,则 = 2, = 1,
m EC1 0
m ( 2,2, 1)
设直线 1与平面 1 1所成角为 ,
9
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
则 m AC 2 3sin | cos m, AC | 1 . 1
m , AC 3 2 3 91
→
(2)由正方体可得,平面 1 1的一个法向量为 = (2, 2,0),
DB m 8 2 2
则 cos DB,m .
DB m 3 2 2 3
因为二面角 1 1 为锐二面角,
→ → 1
所以二面角 1 1 的正弦值为 √1 cos
2 , = .
3
(3)存在,设 F 点的坐标为(t,2,0),所以 1 = ( , 0,2)
→
平面 1 1的一个法向量为 = ( 2,2, 1),
→
因为 1 ⊥ ,所以 1 = 0,t = 1
因为 1 平面 1 1,所以 1 //平面 1 1.此时 = 1
20.解:(1)
1 1
∈ [1,+∞), ′( ) = + ( 2) 1 + = ( 1) ( )
x
1 1
当 ≥ 1时x 1 ≥ 0,ex ≥ , ≤ 1, > ∴ ′( ) ≥ 0, ( )单调递增
1 1
(2) ′( ) = ( 1) 1 + = ( 1)( ).
1 1 1
令 ( ) = ,则 ′( ) = + > 0,所以 ( )在[ , 1]上单调递增,
2 4
因为 1
1
( ) = 2 2 < 0, (1) = 1 > 0,
2
1 1
所以存在 0 ∈ ( , 1),使得 ( 0) = 0,即
0 = ,即ln 0 = , 2 00
1
故当 ∈ [ , 0)时, ( ) < 0,当 ∈ ( 0, 1]时, ( ) > 0, 4
1 1
又当 ∈ [ , 1]时, 1 ≤ 0(等号仅在 = 1时成立),所以当 ∈ [ , )时, ′( ) > 0,
4 4 0
当 ∈ ( 0, 1]时, ′( ) ≤ 0(等号仅在 = 1时成立),
1
所以 ( )在[ ,
4 0
)上单调递增,在( 0, 1]上单调递减,
1 2
则 ( )max = ( 0) = ( 0 2)
0 0 + ln 0 = ( 0 2) 0 0 = 1 2 , 0 00
2 1
令 2 2(1
2) 1
( ) = 1 2 , ∈ ( , 1),则 ′( ) = 2 2 = 2 > 0( ∈ ( , 1)), 2 2
10
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
1 1
所以 ( )在( , 1)上单调递增,则 ( ) > ( ) = 4, ( ) < (1) = 3,
2 2
所以 4 < ( ) < 3,所以 = 4.
21.(Ⅰ)解: . ………3A4 : 2,1, 4,5
分
(Ⅱ)证法一:
证明:由已知,b1 a1 (a1 an ) ,b2 a1 a2 b1 a2 (a1 an ) .
因此,猜想b a ( 1)i (a a ) . ………………4 分 i i 1 n
① 当 i 1时,b1 a1 (a1 an ) ,猜想成立;
② k 假设 i k (k *N ) 时,bk ak ( 1) (a1 an ) .
当 i k 1时,bk 1 ak ak 1 bk
ak ak 1 [ak ( 1)
k (a 1 an )]
ak ak 1 ak ( 1)
k (a1 an )
a ( 1)k 1(a a ) k 1 1 n
故当 i k 1时猜想也成立.
由 ①、② 可知,对于任意正整数 i ,有bi ai ( 1)
i (a a ) . ………………7 分 1 n
设数列Bn 的“衍生数列”为Cn ,则由以上结论可知
c b ( 1)i (b b ) a ( 1)i (a a ) ( 1)ii i n i n (b ,其中1 1 1 bn) i 1,2,3, ,n .
由于n 为偶数,所以bn an ( 1)
n (a1 an ) a1 ,
所以 ci ai ( 1)
i (a1 an ) ( 1)
i (an a1) ai ,其中 i 1,2,3, ,n .
因此,数列Cn 即是数列 An . ………………9 分
证法二:
因为 b1 an ,
b1 b2 a1 a2 ,
b2 b3 a2 a3 ,
……
bn 1 bn an 1 an ,
n
由于n 为偶数,将上述 n 个等式中的第2,4,6, ,n这 个式子都乘以 1,相加得
2
b1 (b1 b2 ) (b2 b3) (bn 1 bn ) an (a1 a2 ) (a2 a3) (an 1 an )
即 bn a1,bn a1 . ………………7 分
由于a1 bn , ai bi 1 bi ai 1 (i 2,3, ,n),
根据“衍生数列”的定义知,数列 An 是 Bn 的“衍生数列”. ………………9 分
(Ⅲ)证法一:
证明:设数列 X n , Yn , Zn 中后者是前者的“衍生数列”.欲证 i 成等差数列,只需证明
x , y , z 成等差数列,即只要证明2yi xi z (i 1,2,3, ,n)i i i i 即可. ……10 分
11
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
由(Ⅱ)中结论可知 yi xi ( 1)
i (x x ), 1 n
zi y ( 1)
i (y y i 1 n )
xi ( 1)
i (x1 xn ) ( 1)
i (y1 yn )
xi ( 1)
i (x x i n 1 n ) ( 1) [xn xn ( 1) (x1 xn)]
xi ( 1)
i (x1 xn) ( 1)
i (x x ) 1 n
xi 2( 1)
i (x , 1 xn )
所以, x z 2x 2( 1)i (x x ) 2y ,即 xi , yi , zi 成等差数列, i i i 1 n i
所以 i 是等差数列. ………………13 分
证法二:
因为 bi ai 1 ai bi 1 (i 2,3,4, ,n) ,
所以 bi ai (bi 1 ai 1) (i 2,3,4, ,n) .
所以欲证 i 成等差数列,只需证明 1 成等差数列即可. ………………10 分
对于数列 An 及其“衍生数列” Bn ,
因为 b1 an ,
b1 b2 a1 a2 ,
b2 b3 a2 a3 ,
……
bn 1 bn an 1 an ,
n 1
由于n 为奇数,将上述 n 个等式中的第2,4,6, ,n 1这 个式子都乘以 1,
2
相加得
b1 (b1 b2 ) (b2 b3) (bn 1 bn ) an (a1 a2 ) (a2 a3) (an 1 an )
即bn an a1 an 2an a1 .
设数列Bn 的“衍生数列”为Cn ,
因为 b1 an ,c1 bn 2an a1 ,
所以 2b1 a1 c1, 即a1,b1,c1成等差数列.
同理可证,b1,c1,d1;c1,d1,e1, 也成等差数列.
即 1 是等差数列.
所以 i 成等差数列. ………………13 分
12
{#{QQABCQiEogAoQAIAARhCAw1wCAKQkBGAAAoORAAEMAIAQBFABCA=}#}
同课章节目录
