19.1.2函数的图像课件
文档属性
| 名称 | 19.1.2函数的图像课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 317.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-27 00:00:00 | ||
图片预览


文档简介
课件29张PPT。函数的图象19.1.2学习目标 1.知道函数图象的意义,会观察、分析函数图象中所蕴含的信息。
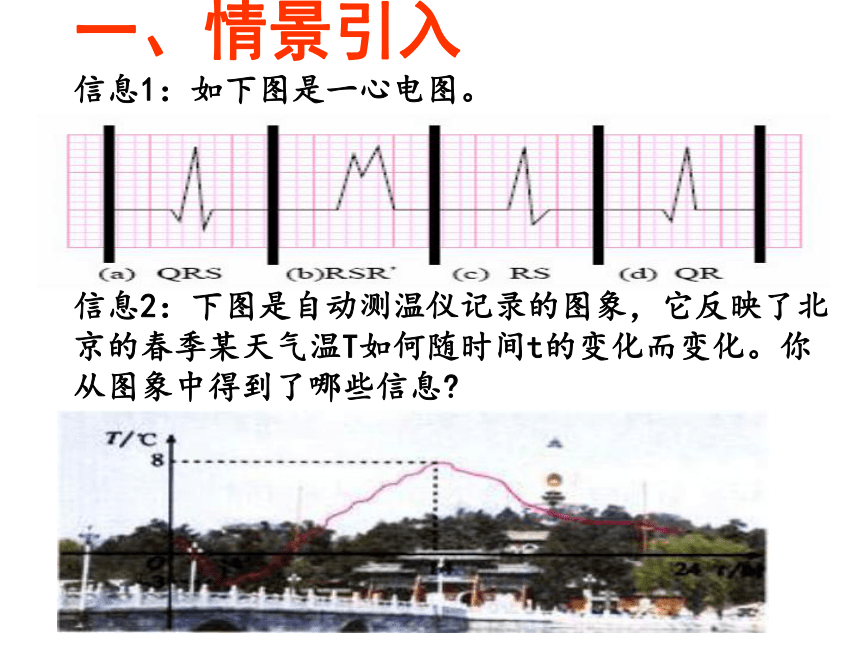
2.能运用数形结合的思想研究抽象的函数。信息1:如下图是一心电图。信息2:下图是自动测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化。你从图象中得到了哪些信息?
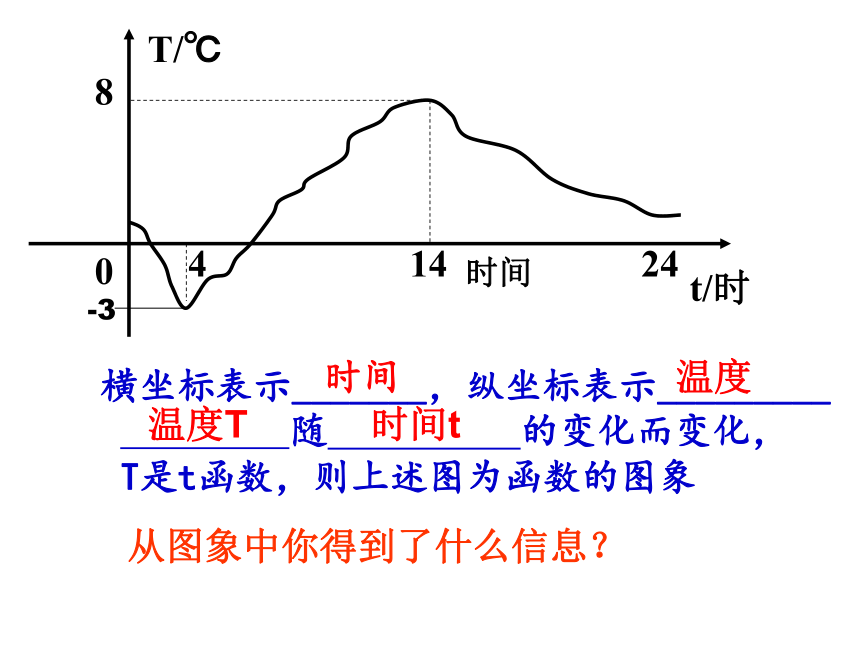
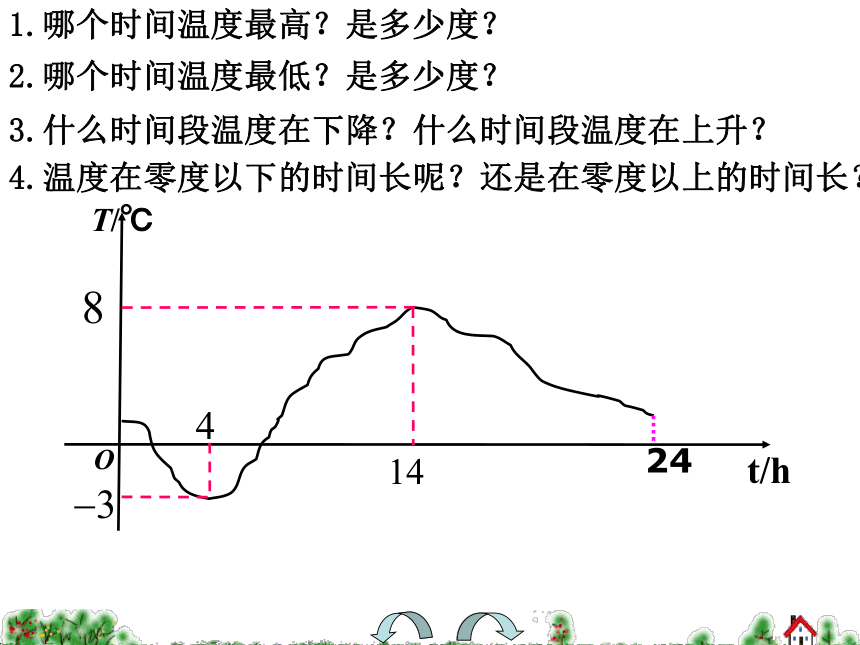
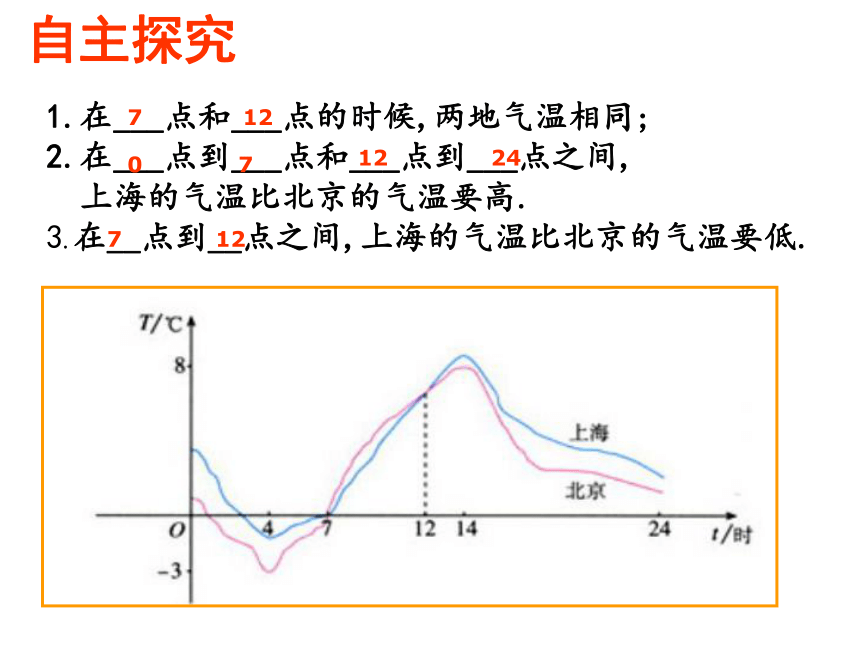
一、情景引入横坐标表示_______,纵坐标表示_________ 随 的变化而变化,T是t函数,则上述图为函数的图象-3时间温度时间温度T时间t从图象中你得到了什么信息?T/℃Ot/h1.哪个时间温度最高?是多少度?2.哪个时间温度最低?是多少度?3.什么时间段温度在下降?什么时间段温度在上升?4.温度在零度以下的时间长呢?还是在零度以上的时间长?24自主探究1.在___点和___点的时候,两地气温相同;
2.在___点到___点和___点到___点之间,
上海的气温比北京的气温要高.
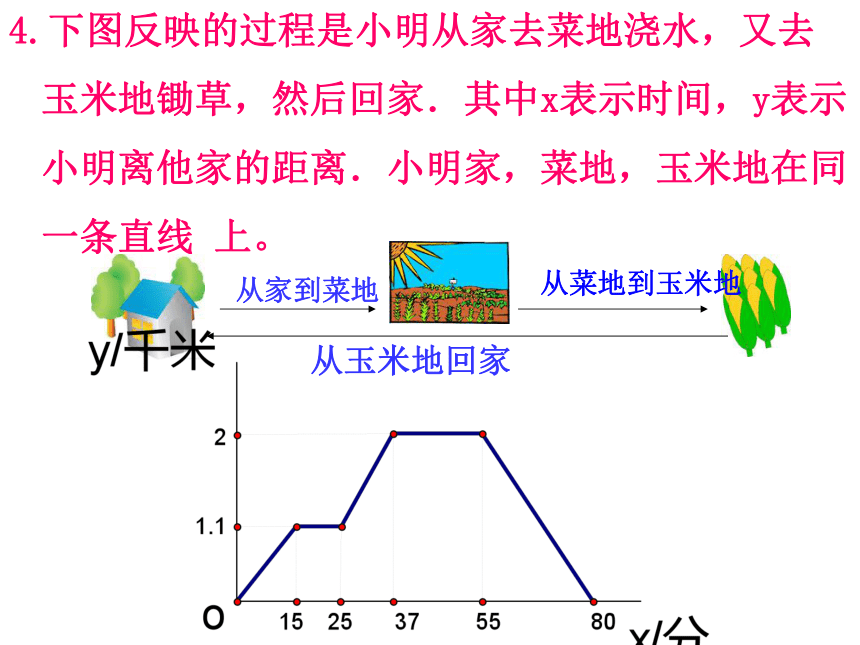
3.在__点到__点之间,上海的气温比北京的气温要低.7127120 712 244.下图反映的过程是小明从家去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小明离他家的距离.小明家,菜地,玉米地在同一条直线 上。小
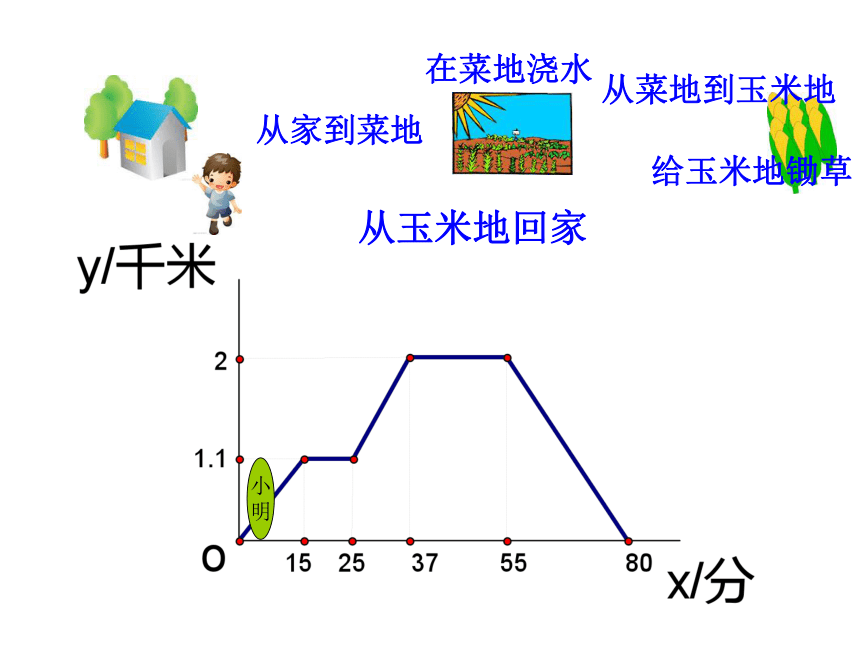
明从家到菜地在菜地浇水从菜地到玉米地给玉米地锄草从玉米地回家小
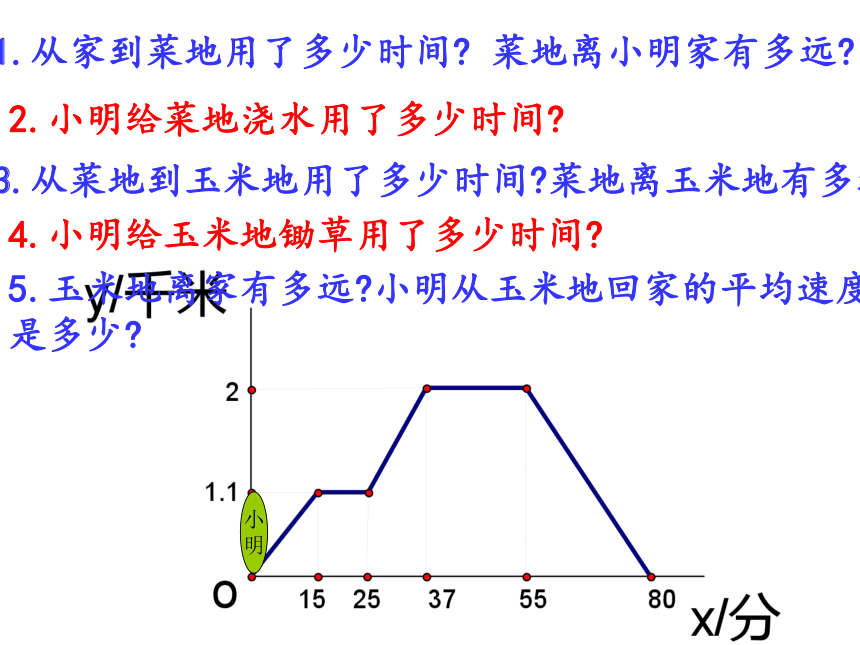
明1.从家到菜地用了多少时间? 菜地离小明家有多远? 2.小明给菜地浇水用了多少时间?3.从菜地到玉米地用了多少时间?菜地离玉米地有多远4.小明给玉米地锄草用了多少时间?5.玉米地离家有多远?小明从玉米地回家的平均速度是多少?. 1.如图,小明家、食堂、图书馆在同一条直
线上,小明从家去食堂吃早餐,接着去图书馆读报,
然后回家.下图反映了这个过程中,小明离他家的距
离y与时间x之间的对应关系.825285868x/分 0.8 0.6 y/千米 O 根据图象回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时间?学以致用825285868x/min 0.8 0.6 y/km O 根据图象回答下列问题:
(2)小明吃早餐用了多少时间?825285868x/分 0.8 0.6 y/千米 O 根据图象回答下列问题:
(3)食堂离图书馆多远?小明从食堂到图书馆用了多少时间? 825285868x/min 0.8 0.6 y/km O 根据图象回答下列问题:
(4)小明读报用了多长时间?825285868x/min 0.8 0.6 y/km O 根据图象回答下列问题:
(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?学以致用2、小明的爷爷吃过晚饭后,出门散步,在报亭看了一会儿报纸才回家,小明绘制了爷爷离家的路程s(米)与外出的时间t(分)之间的关系图.填空:
(1)报亭离爷爷家________米;
(2)爷爷在报亭看了________分钟报纸;
(3)爷爷走去报亭的平均速度是___米/分。 对自己说我有哪些收获? 对老师说你还有哪些困惑? 对同学有哪些温馨提示?畅所欲言活动六:做一做1.如果A、B两人在一次百米赛跑中,路程s(米)与赛跑的时间t(秒)的关系如图所示,则下列说法正确的是( )
(A) A比B先出发 (B) A、B两人的速度相同
(C) A先到达终点 (D) B比A跑的路程多C2.某人早上进行登山活动,从山脚到山顶休息一会儿又沿原路返回,若用横轴表示时间t,纵轴表示与山脚距离h,那么下列四个图中反映全程h与t的关系图是( )D3、下图表示一辆汽车的速度随时间变化的情况:①汽车行驶了多长时间?它的最高时速是多少?
②汽车在哪些时间段保持匀速行驶?时速分别是多少?
③出发后8分到10分之间可能发生了什么情况?
④用自己的语言大致描述这辆汽车的行驶情况.6.甲,乙两同学骑自行车从A地沿同一条路到B地,
已知乙比甲先出发.他们离出发地的距离s/km和
骑行时间t/h之间的函数关系如图所示,给出下列说法:
a.他们都骑了20km;b.乙在途中停留了0.5h;
c.甲和乙两人同时到达目的地;d.甲乙两人途中
没有相遇过.根据图象信息,以上说法正确的是s/kmt/hA.1个B.2个D.4个C.3个甲乙B一、画函数的图象:S = x2(x>0)1、列表:2、描点:3、连线:用平滑曲线去连接画出的点用空心圈表示不在曲线的点10.25492.256.2500… 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象。
函数的图象的意义:归纳一:3、连线函数图象的画法:1、列表2、描点列出自变量与函数的对应值表。
注意:自变量的值(满足取值范围),并取值要适当,以便画图.建立直角坐标系,以自变量的值为横坐标,
相应的函数值为纵坐标,描出表格中数值
对应的各点按照横坐标从小到大的顺序把描出的点用
平滑曲线依次连接起来归纳二:注:函数图象可能是曲线,也可能是直线,也可能是线段或射线,函数图象的形状取决于函数关系和自变量的取值范围。1、画出函数 y = x + 1的图象1、列表解:2、描点3、连线巩固1、作出函数y= (x>0) 的图象。解(1)列表:(2)描点:(3)连线:.图象上的点与函数关系式的关系:(1)函数图象上的任意点(x,y)中的x、y满足函数关系式;
(2)满足函数关系式的任意一对(x,y)的值,所对应的点一定在函数图象上。
归纳三:课堂练习(一):1、已知点(-1,2)是函数y=kx的图象上的一点,则
k= 。2、下列各点中,在函数y= 图象上的是( )
A.(-2,-4) B.(4,4) C.(-2,4) D.(4,2)3、点A(1,m)在函数y=2x的图象上,则点的坐标是( )
A.(1,3) B.(1,2) C.(1,1) D.(2,1)-2DB4.下列四个点中在函数y=2x—3的图象上有( )个 (1,2) 、(3,3) 、(-1, -1)、 (1.5,0) A.1 B.2 C.3 D.4B一、函数的图象的意义:二、函数图象的画法:三、从函数图象中获取有用的信息列表、描点、连线 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象。
课堂小结
2.能运用数形结合的思想研究抽象的函数。信息1:如下图是一心电图。信息2:下图是自动测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化。你从图象中得到了哪些信息?
一、情景引入横坐标表示_______,纵坐标表示_________ 随 的变化而变化,T是t函数,则上述图为函数的图象-3时间温度时间温度T时间t从图象中你得到了什么信息?T/℃Ot/h1.哪个时间温度最高?是多少度?2.哪个时间温度最低?是多少度?3.什么时间段温度在下降?什么时间段温度在上升?4.温度在零度以下的时间长呢?还是在零度以上的时间长?24自主探究1.在___点和___点的时候,两地气温相同;
2.在___点到___点和___点到___点之间,
上海的气温比北京的气温要高.
3.在__点到__点之间,上海的气温比北京的气温要低.7127120 712 244.下图反映的过程是小明从家去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小明离他家的距离.小明家,菜地,玉米地在同一条直线 上。小
明从家到菜地在菜地浇水从菜地到玉米地给玉米地锄草从玉米地回家小
明1.从家到菜地用了多少时间? 菜地离小明家有多远? 2.小明给菜地浇水用了多少时间?3.从菜地到玉米地用了多少时间?菜地离玉米地有多远4.小明给玉米地锄草用了多少时间?5.玉米地离家有多远?小明从玉米地回家的平均速度是多少?. 1.如图,小明家、食堂、图书馆在同一条直
线上,小明从家去食堂吃早餐,接着去图书馆读报,
然后回家.下图反映了这个过程中,小明离他家的距
离y与时间x之间的对应关系.825285868x/分 0.8 0.6 y/千米 O 根据图象回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时间?学以致用825285868x/min 0.8 0.6 y/km O 根据图象回答下列问题:
(2)小明吃早餐用了多少时间?825285868x/分 0.8 0.6 y/千米 O 根据图象回答下列问题:
(3)食堂离图书馆多远?小明从食堂到图书馆用了多少时间? 825285868x/min 0.8 0.6 y/km O 根据图象回答下列问题:
(4)小明读报用了多长时间?825285868x/min 0.8 0.6 y/km O 根据图象回答下列问题:
(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?学以致用2、小明的爷爷吃过晚饭后,出门散步,在报亭看了一会儿报纸才回家,小明绘制了爷爷离家的路程s(米)与外出的时间t(分)之间的关系图.填空:
(1)报亭离爷爷家________米;
(2)爷爷在报亭看了________分钟报纸;
(3)爷爷走去报亭的平均速度是___米/分。 对自己说我有哪些收获? 对老师说你还有哪些困惑? 对同学有哪些温馨提示?畅所欲言活动六:做一做1.如果A、B两人在一次百米赛跑中,路程s(米)与赛跑的时间t(秒)的关系如图所示,则下列说法正确的是( )
(A) A比B先出发 (B) A、B两人的速度相同
(C) A先到达终点 (D) B比A跑的路程多C2.某人早上进行登山活动,从山脚到山顶休息一会儿又沿原路返回,若用横轴表示时间t,纵轴表示与山脚距离h,那么下列四个图中反映全程h与t的关系图是( )D3、下图表示一辆汽车的速度随时间变化的情况:①汽车行驶了多长时间?它的最高时速是多少?
②汽车在哪些时间段保持匀速行驶?时速分别是多少?
③出发后8分到10分之间可能发生了什么情况?
④用自己的语言大致描述这辆汽车的行驶情况.6.甲,乙两同学骑自行车从A地沿同一条路到B地,
已知乙比甲先出发.他们离出发地的距离s/km和
骑行时间t/h之间的函数关系如图所示,给出下列说法:
a.他们都骑了20km;b.乙在途中停留了0.5h;
c.甲和乙两人同时到达目的地;d.甲乙两人途中
没有相遇过.根据图象信息,以上说法正确的是s/kmt/hA.1个B.2个D.4个C.3个甲乙B一、画函数的图象:S = x2(x>0)1、列表:2、描点:3、连线:用平滑曲线去连接画出的点用空心圈表示不在曲线的点10.25492.256.2500… 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象。
函数的图象的意义:归纳一:3、连线函数图象的画法:1、列表2、描点列出自变量与函数的对应值表。
注意:自变量的值(满足取值范围),并取值要适当,以便画图.建立直角坐标系,以自变量的值为横坐标,
相应的函数值为纵坐标,描出表格中数值
对应的各点按照横坐标从小到大的顺序把描出的点用
平滑曲线依次连接起来归纳二:注:函数图象可能是曲线,也可能是直线,也可能是线段或射线,函数图象的形状取决于函数关系和自变量的取值范围。1、画出函数 y = x + 1的图象1、列表解:2、描点3、连线巩固1、作出函数y= (x>0) 的图象。解(1)列表:(2)描点:(3)连线:.图象上的点与函数关系式的关系:(1)函数图象上的任意点(x,y)中的x、y满足函数关系式;
(2)满足函数关系式的任意一对(x,y)的值,所对应的点一定在函数图象上。
归纳三:课堂练习(一):1、已知点(-1,2)是函数y=kx的图象上的一点,则
k= 。2、下列各点中,在函数y= 图象上的是( )
A.(-2,-4) B.(4,4) C.(-2,4) D.(4,2)3、点A(1,m)在函数y=2x的图象上,则点的坐标是( )
A.(1,3) B.(1,2) C.(1,1) D.(2,1)-2DB4.下列四个点中在函数y=2x—3的图象上有( )个 (1,2) 、(3,3) 、(-1, -1)、 (1.5,0) A.1 B.2 C.3 D.4B一、函数的图象的意义:二、函数图象的画法:三、从函数图象中获取有用的信息列表、描点、连线 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象。
课堂小结
