5.2.2平行线的判定课件
文档属性
| 名称 | 5.2.2平行线的判定课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 734.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-30 00:00:00 | ||
图片预览





文档简介
课件27张PPT。5.2.2 平行线的判定
本课学习由平行线的定义难以判断两条直线平行引入对于平行线判定方法的探究.先由平行线的画法得到判定方法 1,再经过简单推理得到判定方法 2和判定方法 3. 学情分析学习目标:
(1)理解平行线的判定方法.
(2)经历平行线判定的探究过程,从中体会转化的思想和研究平行线判定的方法.
学习重点:
平行线判定方法的应用。
学习难点:
平行线判定方法的过程。
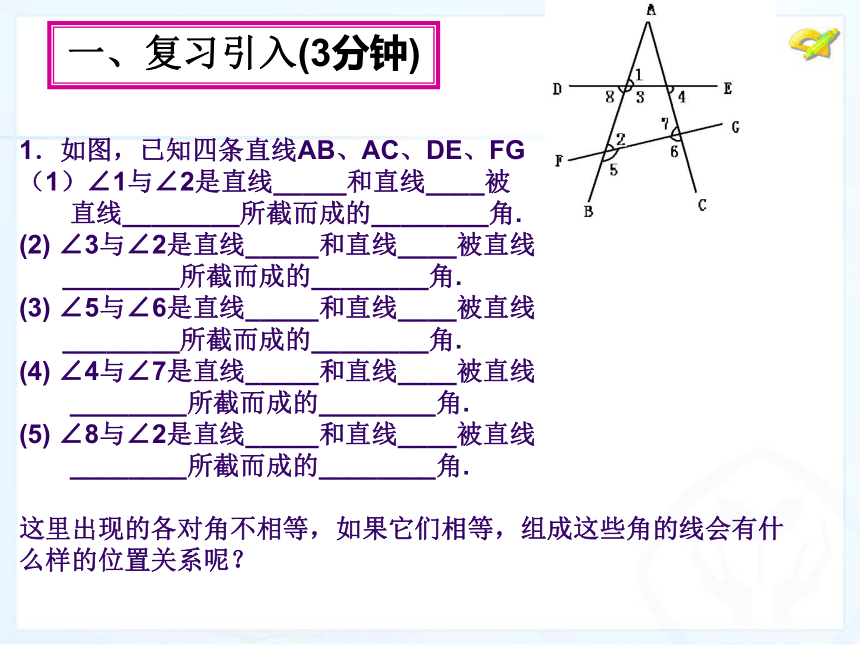
1.如图,已知四条直线AB、AC、DE、FG (1)∠1与∠2是直线_____和直线____被 直线________所截而成的________角. (2) ∠3与∠2是直线_____和直线____被直线 ________所截而成的________角. (3) ∠5与∠6是直线_____和直线____被直线 ________所截而成的________角. (4) ∠4与∠7是直线_____和直线____被直线 ________所截而成的________角. (5) ∠8与∠2是直线_____和直线____被直线 ________所截而成的________角. 这里出现的各对角不相等,如果它们相等,组成这些角的线会有什么样的位置关系呢?一、复习引入(3分钟)二、问题引入:(10分钟) 阅读课本第12页至第13页,思考以下问题:
1、结合第12页“思考”,经历判定方法1的归纳过程,并口述判定方法1的内容。
2、判定方法1的条件和结论分别是什么?用“因为、所以”写出推理过程。
3、判定方法2、3是由什么推导出来的?叙述并表达判定方法2、3。
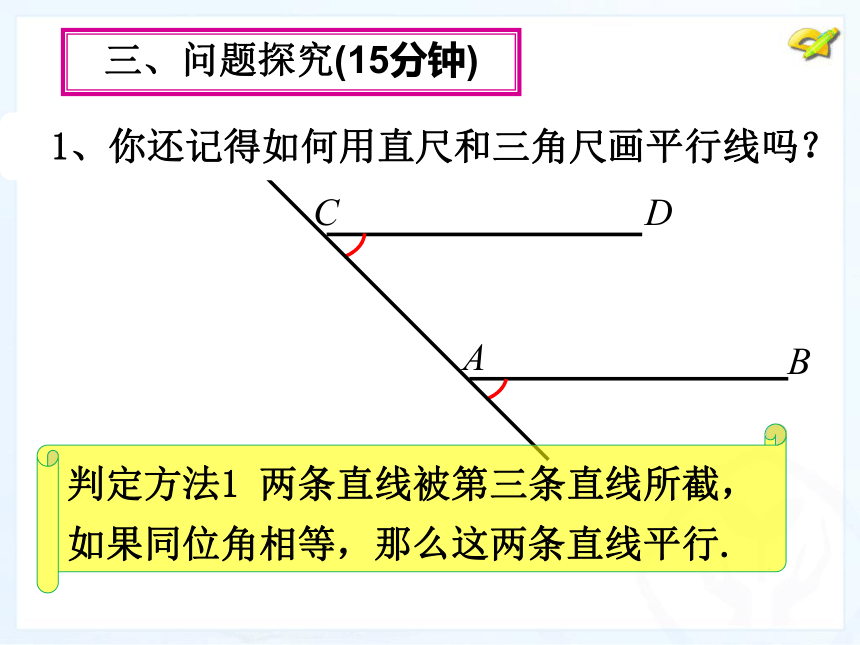
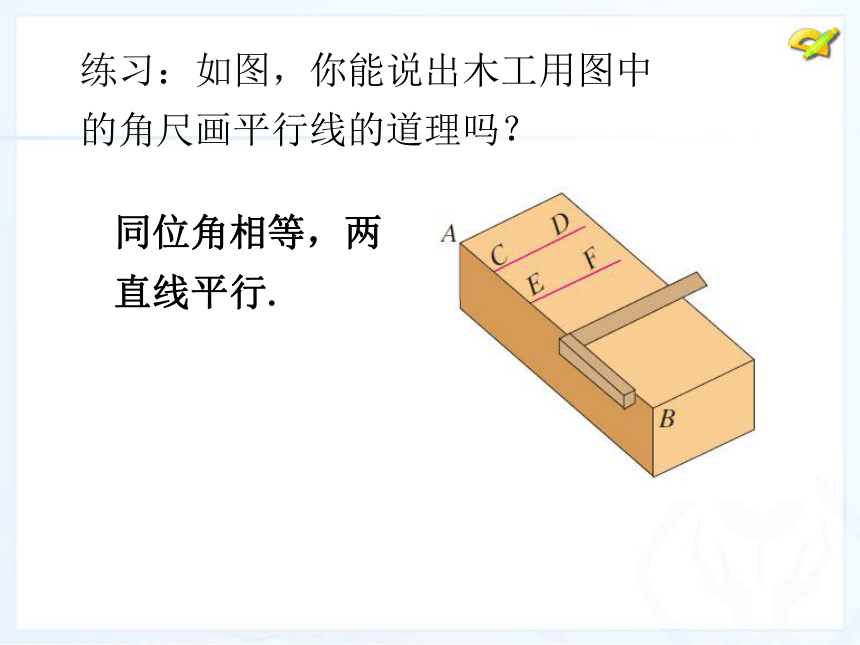
4、归纳平行线的判定方法。2、平行线的画法:三、问题探究(15分钟) 1、你还记得如何用直尺和三角尺画平行线吗?判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.同位角相等,两直线平行.练习:如图,你能说出木工用图中的角尺画平行线的道理吗? 如果∠1=∠7,能得出AB∥CD吗?(作业1)2、思考解:∵∠1=∠7
∠1=∠3
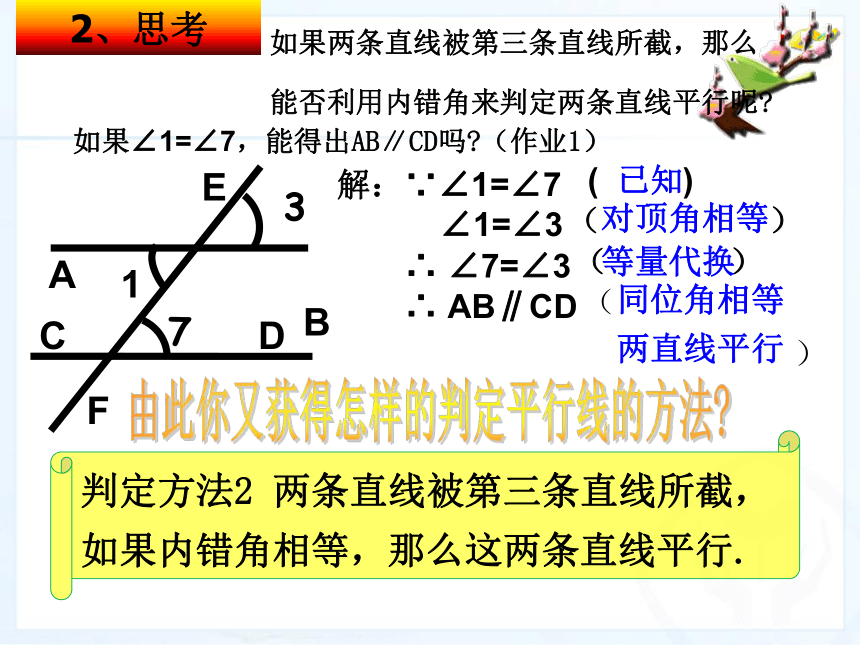
∴ ∠7=∠3∴ AB∥CDB由此你又获得怎样的判定平行线的方法?
( ) 已知 ( ) 对顶角相等( ) 等量代换 (
)
同位角相等
两直线平行 判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.如果两条直线被第三条直线所截,那么
能否利用内错角来判定两条直线平行呢? 做一做 如图,已知
说出其中的平行线,并说明理由。 如果∠4+∠7=180°,能得出AB∥CD?3、思考EF解:∵ ∠4+∠7=180 °(已知)
∠4+∠1=180°(邻补角的定义)∴ ∠7=∠1(同角的补角相等)∴ AB∥CD(内错角相等,
两直线平行)判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?如图:直线AB、CD都和AE相交,
且∠1+∠A=180o .
求证:AB//CDE 证明:∵∠1+∠A=180o练习∴∠2+∠A=180o∴( )( )( )( )已知对顶角相等等量代换同旁内角互补,
两直线平行∠1=∠2AB∥CD公理:
同位角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.判定定理1:
内错角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.判定定理2:
同旁内角互补,两直线平行.
∵∠1+∠2=1800 , ∴ a∥b. 这里的结论,以后可以直接运用. 4、归纳平行线的判定(1)由∠CBE=∠A可以判定哪两条直线平行?
根据是什么?5.巩固新知,深化理解例1 如图, BE是AB的延长线.答: AD∥BC .根据同位角相等,两直线平行.(2)由∠CBE=∠C可以判定哪两条直线平行?
根据是什么?例1如图, BE是AB的延长线.答: AE∥CD .根据内错角相等,两直线平行.(3)由∠D+∠A= 180°可以判定哪两条直线平
行?根据是什么?例2 如图, BE是AB的延长线.答: AE∥CD .根据同旁内角互补,两直线平行.已知条件:直线b与直线c都垂直于直线a.
要说明的结论:直线b与直线c平行吗?例3、在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?学会分析,应用方法已知:直线b与直线c都垂直于直线a.
说明:直线b与直线c平行吗?答:b‖c理由是:
∵ b⊥a, c ⊥a (已知)
∴ ∠1= ∠2 = 90°(垂直的定义)
∴ b∥c(同位角相等,两直线平行).12你还能用其他方法说明理由吗?理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)abc12解法2:∵ b⊥a,c⊥a (已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)c解法3:1.如图,
(1)从∠1=∠2,可以推出 ∥
理由是
(2)从∠2=∠ ,可以推出c∥d ,
理由是
(3)如果∠4=75°,∠3=75 °,
可以推出 ∥
(4) 从∠4=75°,∠5= °,
可以推出a∥b.
四、课堂测试dba内错角相等,两直线平行同位角相等,两直线平行.3 cdc105(15分钟)2.如图,你可以添加哪些条件使得
AB∥CD?课堂测试3、 小明用如图所示的方法作出了平行线,你认为他的作法对吗?为什么?1、如图,已知:∠1+∠2=180°,求证:AB∥CD.证明:∵∠1+∠2=180°(已知),
∠1=∠3 ,∠2=∠4 (对顶角相等) ∴∠3+ =180°(等量代换)
∴ ∥ .
(同旁内角互补,两直线平行)∠4AB CD五、应用迁移,深化理解答: AB∥CD .
理由如下:
∵ AC平分∠BAD,
∴ ∠1=∠3 .
∵∠1=∠2,
∴ ∠2=∠3 .
∵ ∠2和∠3是内错角,
∴ AB∥CD(内错角相等,两直线平行).2、 已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,AB与CD平行吗?为什么?3、如图,已知直线AB、BC、CD、DA相交于A、B、C、D, ∠1=∠2,∠2+∠=180°,求证:(1)AB||CD; (2)AD||BC
4、看图填空:
∵ ∠2+∠1=180° (已知 )
∴ a||b( )
∵ ∠3+∠1=180° (已知 )
∴ a||c( )
∵ a||c, a||b (已证)
∴ b||c ( )
(1)本节课,你学习了哪些平行线的判定方法?五.归纳小结(2)你能用自己的语言叙述得到平行线判定方法的过程吗?(3)判定方法2和判定方法3是通过简单推理得到的,在推理论证中需要注意哪些问题?(3分钟) 教科书 习题5.2 第1、4、7题六.布置作业教学反思:
培养学生的识图能力,提高分析问题的能力。
(1)理解平行线的判定方法.
(2)经历平行线判定的探究过程,从中体会转化的思想和研究平行线判定的方法.
学习重点:
平行线判定方法的应用。
学习难点:
平行线判定方法的过程。
1.如图,已知四条直线AB、AC、DE、FG (1)∠1与∠2是直线_____和直线____被 直线________所截而成的________角. (2) ∠3与∠2是直线_____和直线____被直线 ________所截而成的________角. (3) ∠5与∠6是直线_____和直线____被直线 ________所截而成的________角. (4) ∠4与∠7是直线_____和直线____被直线 ________所截而成的________角. (5) ∠8与∠2是直线_____和直线____被直线 ________所截而成的________角. 这里出现的各对角不相等,如果它们相等,组成这些角的线会有什么样的位置关系呢?一、复习引入(3分钟)二、问题引入:(10分钟) 阅读课本第12页至第13页,思考以下问题:
1、结合第12页“思考”,经历判定方法1的归纳过程,并口述判定方法1的内容。
2、判定方法1的条件和结论分别是什么?用“因为、所以”写出推理过程。
3、判定方法2、3是由什么推导出来的?叙述并表达判定方法2、3。
4、归纳平行线的判定方法。2、平行线的画法:三、问题探究(15分钟) 1、你还记得如何用直尺和三角尺画平行线吗?判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.同位角相等,两直线平行.练习:如图,你能说出木工用图中的角尺画平行线的道理吗? 如果∠1=∠7,能得出AB∥CD吗?(作业1)2、思考解:∵∠1=∠7
∠1=∠3
∴ ∠7=∠3∴ AB∥CDB由此你又获得怎样的判定平行线的方法?
( ) 已知 ( ) 对顶角相等( ) 等量代换 (
)
同位角相等
两直线平行 判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.如果两条直线被第三条直线所截,那么
能否利用内错角来判定两条直线平行呢? 做一做 如图,已知
说出其中的平行线,并说明理由。 如果∠4+∠7=180°,能得出AB∥CD?3、思考EF解:∵ ∠4+∠7=180 °(已知)
∠4+∠1=180°(邻补角的定义)∴ ∠7=∠1(同角的补角相等)∴ AB∥CD(内错角相等,
两直线平行)判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?如图:直线AB、CD都和AE相交,
且∠1+∠A=180o .
求证:AB//CDE 证明:∵∠1+∠A=180o练习∴∠2+∠A=180o∴( )( )( )( )已知对顶角相等等量代换同旁内角互补,
两直线平行∠1=∠2AB∥CD公理:
同位角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.判定定理1:
内错角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.判定定理2:
同旁内角互补,两直线平行.
∵∠1+∠2=1800 , ∴ a∥b. 这里的结论,以后可以直接运用. 4、归纳平行线的判定(1)由∠CBE=∠A可以判定哪两条直线平行?
根据是什么?5.巩固新知,深化理解例1 如图, BE是AB的延长线.答: AD∥BC .根据同位角相等,两直线平行.(2)由∠CBE=∠C可以判定哪两条直线平行?
根据是什么?例1如图, BE是AB的延长线.答: AE∥CD .根据内错角相等,两直线平行.(3)由∠D+∠A= 180°可以判定哪两条直线平
行?根据是什么?例2 如图, BE是AB的延长线.答: AE∥CD .根据同旁内角互补,两直线平行.已知条件:直线b与直线c都垂直于直线a.
要说明的结论:直线b与直线c平行吗?例3、在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?学会分析,应用方法已知:直线b与直线c都垂直于直线a.
说明:直线b与直线c平行吗?答:b‖c理由是:
∵ b⊥a, c ⊥a (已知)
∴ ∠1= ∠2 = 90°(垂直的定义)
∴ b∥c(同位角相等,两直线平行).12你还能用其他方法说明理由吗?理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)abc12解法2:∵ b⊥a,c⊥a (已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)c解法3:1.如图,
(1)从∠1=∠2,可以推出 ∥
理由是
(2)从∠2=∠ ,可以推出c∥d ,
理由是
(3)如果∠4=75°,∠3=75 °,
可以推出 ∥
(4) 从∠4=75°,∠5= °,
可以推出a∥b.
四、课堂测试dba内错角相等,两直线平行同位角相等,两直线平行.3 cdc105(15分钟)2.如图,你可以添加哪些条件使得
AB∥CD?课堂测试3、 小明用如图所示的方法作出了平行线,你认为他的作法对吗?为什么?1、如图,已知:∠1+∠2=180°,求证:AB∥CD.证明:∵∠1+∠2=180°(已知),
∠1=∠3 ,∠2=∠4 (对顶角相等) ∴∠3+ =180°(等量代换)
∴ ∥ .
(同旁内角互补,两直线平行)∠4AB CD五、应用迁移,深化理解答: AB∥CD .
理由如下:
∵ AC平分∠BAD,
∴ ∠1=∠3 .
∵∠1=∠2,
∴ ∠2=∠3 .
∵ ∠2和∠3是内错角,
∴ AB∥CD(内错角相等,两直线平行).2、 已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,AB与CD平行吗?为什么?3、如图,已知直线AB、BC、CD、DA相交于A、B、C、D, ∠1=∠2,∠2+∠=180°,求证:(1)AB||CD; (2)AD||BC
4、看图填空:
∵ ∠2+∠1=180° (已知 )
∴ a||b( )
∵ ∠3+∠1=180° (已知 )
∴ a||c( )
∵ a||c, a||b (已证)
∴ b||c ( )
(1)本节课,你学习了哪些平行线的判定方法?五.归纳小结(2)你能用自己的语言叙述得到平行线判定方法的过程吗?(3)判定方法2和判定方法3是通过简单推理得到的,在推理论证中需要注意哪些问题?(3分钟) 教科书 习题5.2 第1、4、7题六.布置作业教学反思:
培养学生的识图能力,提高分析问题的能力。
