5.1 相交线(第2课时)课件(共38张PPT)-2023-2024学年七年级数学上册同步精品课堂(华东师大版)
文档属性
| 名称 | 5.1 相交线(第2课时)课件(共38张PPT)-2023-2024学年七年级数学上册同步精品课堂(华东师大版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 00:00:00 | ||
图片预览








文档简介
数学(华东师大版)
七年级 上册
第5章 相交线与平行线
5.1 相交线
第2课时 垂线
学习目标
1.理解垂线的概念及画法;
2. 知道垂线段和点到直线的距离的概念,并会应用解决问题;
导入新课
如图所示,背着沉重货物的小马要过河,它有 3 条线路可以走,选哪一条路走的路程最少呢?睿智的你能帮小马选出最近的路吗?
导入新课
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
导入新课
集思广益:日常生活里,图中的两条直线的关系很常见,你还能举出其他例子吗?
讲授新课
知识点一 垂线的概念
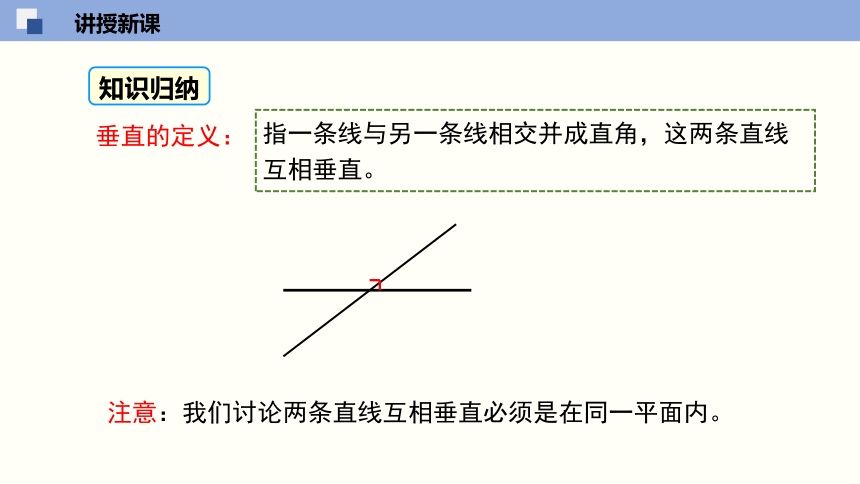
当两条直线相交所构成的四个角中有一个角为直角时,这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线.
垂线定义:
它们的交点叫做垂足.
直线AB、CD互相垂直,记作“AB⊥CD,垂足为 O”.
读作“AB 垂直于 CD”.
讲授新课
在日常生活中,经常可以看到线线互相垂直的图形.
讲授新课
十字路口的两条道路
方格本的横线和竖线
铅垂线和水平线
讲授新课
垂线知识详解:
(1)垂线是直线而不是线段或射线: 遇到线段与射线的垂直问题,都是指它们所在的直线互相垂直.
(2)推理格式:如图,因为 AB⊥CD,所以∠AOC=∠COB=∠BOD =∠AOD = 90°.
反过来:因为∠AOC = 90°,所以AB⊥CD.
(3)平面内两直线的位置关系: ①相交;②平行;③重合.其中,垂直是相交的特殊情况,即两条相交直线的夹角为直角.
讲授新课
指一条线与另一条线相交并成直角,这两条直线互相垂直。
注意:我们讨论两条直线互相垂直必须是在同一平面内。
垂直的定义:
知识归纳
讲授新课
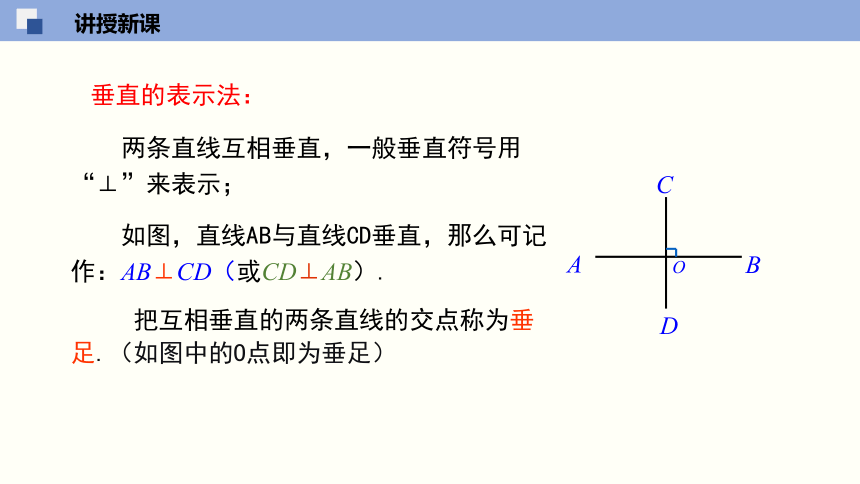
两条直线互相垂直,一般垂直符号用“⊥”来表示;
如图,直线AB与直线CD垂直,那么可记作:AB⊥CD(或CD⊥AB).
把互相垂直的两条直线的交点称为垂足.(如图中的O点即为垂足)
A
B
C
D
O
垂直的表示法:
讲授新课
①判定:两条直线相交成90°
②性质:两条直线互相垂直所形成的四个角均为90°
垂线的基本性质与判定
讲授新课
典例精析
【例1】(1)若直线m、n相交于点O,∠1=90°,则 ;
(2)若直线AB、CD相交于点O,且AB⊥CD,那么∠BOD = _________;
(3)如图,BO⊥AO,∠BOC与∠BOA的度数之比为1:5,那么∠COA=_____,∠BOC的补角为 .
O
m
n
1
B
C
A
O
m⊥n
90°
72°
162°
讲授新课
知识点二 垂线的画法及基本事实
问题:
(1)画已知直线l的垂线能画几条?
(2)过直线l上的一点A画l的垂线,这样的垂线能画几条?
(3)过直线l外的一点B画l的垂线,这样的垂线能画几条?
问题引导
讲授新课
A
B
C
D
O
符号语言:
如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O.
①判定:∵∠AOD=90°(已知)
∴AB⊥CD(垂直的定义)
符号语言:
反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°.
②性质:∵ AB⊥CD (已知) ∴ ∠AOD=90° (垂直的定义)
(∠AOC=∠BOC=∠BOD=90°)
讲授新课
经过直线 AB 外一点 P,画出垂直于直线 AB 的直线. 这样的垂线能画多少条?
(1)一靠: 将三角尺的一条直角边靠在已知直线上,即一条直角边与已知直线重合.
(2)二过:移动三角尺,使三角尺的另一条直角边经过已知点.
(3)三画:沿已知点所在的直角边画线,则这条直线就是经过已知点画的已知直线的垂线.
只能画一条垂线
讲授新课
经过直线 AB 上一点 P,画出垂直于直线 AB 的直线. 这样的垂线能画多少条?
只能画一条垂线
由上述操作可以得到关于垂线的一个基本事实:
过一点有且只有一条直线与已知直线垂直.
讲授新课
过一点有且只有一条直线与已知直线垂直.
(1)“过一点”中的点,可以在已知直线上,也可以在已知直线外;
(2)“有且只有”中,“有”指存在,“只有”指唯一性.
注意:
总结归纳
讲授新课
典例精析
【例2】过点A画线段BC所在直线的垂线段,其中正确的是(????)
A. B.
C. D.
【答案】D
【分析】根据垂线段的定义依次判断每个选项.
讲授新课
练一练
1.如图,一束光线以入射角为50°的角度射向斜放在地面AB上的平面镜CD,经平面镜反射后与水平面成30°的角,则CD与地面AB所成的角∠CDA的度数是_____.
【详解】解:过点E作EM⊥CD于E.
根据题意得:∠1=∠2=50°,∠END=30°,
∴∠DEN=40°,
∴∠CDA=∠DEN+∠END=30°+40°=70°.
故答案为70°.
讲授新课
知识点三 垂线段及点到直线的距离
A
B
C
D
E
l
连接直线外一点与直线上各点的所有线段中垂线段最短.
线段AD的长度叫做点A到直线l的距离.
讲授新课
C
D
E
l
B
A
过河问题
如图,小明要从A点过河,目测有B、C、D、E四个地点,哪个地点的距离是最短的?
讲授新课
连接直线外一点与直线上各点的所有线段中,垂线段最短.简单说成:垂线段最短.
概念归纳
D
l
A
讲授新课
垂线的性质: 在同一平面内,过一点有且只有一条直线与已知直线垂直.
垂线的性质中,经过的这“一点”的位置可以在已知直线上,也可以在已知直线外;“有且只有”的含义既表示了存在性,又表示了唯一性.
讲授新课
连结直线外一点和直线上各点的线段有无数条,但垂线段只有一条,且垂线段最短说明长度也是唯一的,所以点到直线的距离是唯一的.
讲授新课
垂线、垂直与垂线段的关系:
①区别:
垂线是一条与已知直线垂直的直线;
垂直是两条直线之间的位置关系;
垂线段是一条与已知直线垂直的线段.
②联系:
垂线段所在的直线是已知直线的垂线;
垂线段所在的直线与已知直线垂直.
讲授新课
典例精析
【例3】过点P向线段AB所在直线引垂线,正确的是( )
A B C D
C
讲授新课
练一练
1.两条直线相交所成的四个角中,下列条件中能判定两条直线垂直的是( )
A. 有两个角相等 B.有两对角相等
C. 有三个角相等 D.有四对邻补角
C
当堂检测
如图,∠ABD = 90°,在下列各语句中填入适当的文字或数字:
(1)点 B 在直线______________上,点 D 在直线______外;
(2)直线_____与直线_____相交于点 A,点 D 是直线_____与直线_____的交点,也是直线_____与直线______的交点,又是直线_____与直线_____的交点;
(3)直线_____⊥直线______,垂足为点_____;
(4)过点 D 有且只有_____条直线与直线 AC 垂直.
AC(或BD)
AC
AD
AC
AD
BD
AD
CD
BD
CD
BD
AC
B
一
当堂检测
2. 如图,点P在直线AB上,点C,D在直线AB的上方,且PC⊥PD,∠APC=28°,则∠BPD的度数为( )
A. 28°
B. 60°
C. 62°
D. 152°
C
当堂检测
4. 如图,直线AB,CD相交于点O,若∠EOD=40°, ∠BOC=130°, 则射线OE与直线AB的位置关系是____________.
垂直
当堂检测
5.如图,是测量学生跳远成绩的示意图,即PA的长为某同学的跳远成绩,其依据是( )
A.两点之间线段最短 B.两点确定一条直线
C.垂线段最短 D.过一点有且只有一条直线与已知直线垂直
【答案】C
【分析】由点到直线的距离的定义及跳远比赛的规则作出判断.
【详解】解:能正确解释这一现象的数学知识是垂线段最短,
故选:C.
当堂检测
6.如图,AO⊥FD,OD为∠BOC的平分线,OE为射线OB的反向延长线,若∠AOB=40°,求∠EOF、∠COE的度数.
A
F
D
O
B
C
E
解:∵AO⊥OD且∠AOB=40°,
∴∠BOD=90°-40°=50°,
∴∠EOF=50°.
∵OD平分∠BOC,
∴∠DOC=∠BOD=50°,
∴∠COE=180°-50°-50°=80°.
当堂检测
7.如图,OA⊥OB,OC⊥OD,O是垂足,∠AOD=120°,那么∠COB的度数为______;
【详解】解:∵OA⊥OB,OC⊥OD,
∴∠AOB=90°
∵∠AOD=120°
∴∠BOD=120°-90°=30°
∠BOC=60°
故答案为:60°.
当堂检测
8.如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC:∠AOD=7:11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.
【答案】(1)145°
(2)125°
【点睛】本题考查的是邻补角的性质、对顶角的性质和角平分线的定义,垂直的定义,几何图形中角度的计算,掌握邻补角互补、对顶角相等和垂直的定义是解题的关键.
当堂检测
(1)
解:∵∠AOC:∠AOD=7:11,∠AOC+∠AOD=180°
∴∠AOC=????????????×????????????°=????????°,
∴∠DOB=∠AOC=70°,
又∵OE平分∠BOD,
∴∠DOE=????????∠????????????=????????×????????°=????????°,
∴∠COE=180°-∠DOE=180°-35°=145°,
(2)
∵OF⊥OE,
∴∠EOF=90°,
∴∠FOD=90°-∠DOE=90°-35°=55°,
∴∠COF=180°-∠FOD=180°-55°=125°.
?
课堂小结
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
1.垂线的定义
2.垂线的画法
3.垂线的性质
(1)过一点有且只有一条直线与已知直线垂直
一、放;二、靠;三、移 ;四、画.
4.点到直线的距离
(2)垂线段最短
谢 谢~
七年级 上册
第5章 相交线与平行线
5.1 相交线
第2课时 垂线
学习目标
1.理解垂线的概念及画法;
2. 知道垂线段和点到直线的距离的概念,并会应用解决问题;
导入新课
如图所示,背着沉重货物的小马要过河,它有 3 条线路可以走,选哪一条路走的路程最少呢?睿智的你能帮小马选出最近的路吗?
导入新课
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
导入新课
集思广益:日常生活里,图中的两条直线的关系很常见,你还能举出其他例子吗?
讲授新课
知识点一 垂线的概念
当两条直线相交所构成的四个角中有一个角为直角时,这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线.
垂线定义:
它们的交点叫做垂足.
直线AB、CD互相垂直,记作“AB⊥CD,垂足为 O”.
读作“AB 垂直于 CD”.
讲授新课
在日常生活中,经常可以看到线线互相垂直的图形.
讲授新课
十字路口的两条道路
方格本的横线和竖线
铅垂线和水平线
讲授新课
垂线知识详解:
(1)垂线是直线而不是线段或射线: 遇到线段与射线的垂直问题,都是指它们所在的直线互相垂直.
(2)推理格式:如图,因为 AB⊥CD,所以∠AOC=∠COB=∠BOD =∠AOD = 90°.
反过来:因为∠AOC = 90°,所以AB⊥CD.
(3)平面内两直线的位置关系: ①相交;②平行;③重合.其中,垂直是相交的特殊情况,即两条相交直线的夹角为直角.
讲授新课
指一条线与另一条线相交并成直角,这两条直线互相垂直。
注意:我们讨论两条直线互相垂直必须是在同一平面内。
垂直的定义:
知识归纳
讲授新课
两条直线互相垂直,一般垂直符号用“⊥”来表示;
如图,直线AB与直线CD垂直,那么可记作:AB⊥CD(或CD⊥AB).
把互相垂直的两条直线的交点称为垂足.(如图中的O点即为垂足)
A
B
C
D
O
垂直的表示法:
讲授新课
①判定:两条直线相交成90°
②性质:两条直线互相垂直所形成的四个角均为90°
垂线的基本性质与判定
讲授新课
典例精析
【例1】(1)若直线m、n相交于点O,∠1=90°,则 ;
(2)若直线AB、CD相交于点O,且AB⊥CD,那么∠BOD = _________;
(3)如图,BO⊥AO,∠BOC与∠BOA的度数之比为1:5,那么∠COA=_____,∠BOC的补角为 .
O
m
n
1
B
C
A
O
m⊥n
90°
72°
162°
讲授新课
知识点二 垂线的画法及基本事实
问题:
(1)画已知直线l的垂线能画几条?
(2)过直线l上的一点A画l的垂线,这样的垂线能画几条?
(3)过直线l外的一点B画l的垂线,这样的垂线能画几条?
问题引导
讲授新课
A
B
C
D
O
符号语言:
如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O.
①判定:∵∠AOD=90°(已知)
∴AB⊥CD(垂直的定义)
符号语言:
反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°.
②性质:∵ AB⊥CD (已知) ∴ ∠AOD=90° (垂直的定义)
(∠AOC=∠BOC=∠BOD=90°)
讲授新课
经过直线 AB 外一点 P,画出垂直于直线 AB 的直线. 这样的垂线能画多少条?
(1)一靠: 将三角尺的一条直角边靠在已知直线上,即一条直角边与已知直线重合.
(2)二过:移动三角尺,使三角尺的另一条直角边经过已知点.
(3)三画:沿已知点所在的直角边画线,则这条直线就是经过已知点画的已知直线的垂线.
只能画一条垂线
讲授新课
经过直线 AB 上一点 P,画出垂直于直线 AB 的直线. 这样的垂线能画多少条?
只能画一条垂线
由上述操作可以得到关于垂线的一个基本事实:
过一点有且只有一条直线与已知直线垂直.
讲授新课
过一点有且只有一条直线与已知直线垂直.
(1)“过一点”中的点,可以在已知直线上,也可以在已知直线外;
(2)“有且只有”中,“有”指存在,“只有”指唯一性.
注意:
总结归纳
讲授新课
典例精析
【例2】过点A画线段BC所在直线的垂线段,其中正确的是(????)
A. B.
C. D.
【答案】D
【分析】根据垂线段的定义依次判断每个选项.
讲授新课
练一练
1.如图,一束光线以入射角为50°的角度射向斜放在地面AB上的平面镜CD,经平面镜反射后与水平面成30°的角,则CD与地面AB所成的角∠CDA的度数是_____.
【详解】解:过点E作EM⊥CD于E.
根据题意得:∠1=∠2=50°,∠END=30°,
∴∠DEN=40°,
∴∠CDA=∠DEN+∠END=30°+40°=70°.
故答案为70°.
讲授新课
知识点三 垂线段及点到直线的距离
A
B
C
D
E
l
连接直线外一点与直线上各点的所有线段中垂线段最短.
线段AD的长度叫做点A到直线l的距离.
讲授新课
C
D
E
l
B
A
过河问题
如图,小明要从A点过河,目测有B、C、D、E四个地点,哪个地点的距离是最短的?
讲授新课
连接直线外一点与直线上各点的所有线段中,垂线段最短.简单说成:垂线段最短.
概念归纳
D
l
A
讲授新课
垂线的性质: 在同一平面内,过一点有且只有一条直线与已知直线垂直.
垂线的性质中,经过的这“一点”的位置可以在已知直线上,也可以在已知直线外;“有且只有”的含义既表示了存在性,又表示了唯一性.
讲授新课
连结直线外一点和直线上各点的线段有无数条,但垂线段只有一条,且垂线段最短说明长度也是唯一的,所以点到直线的距离是唯一的.
讲授新课
垂线、垂直与垂线段的关系:
①区别:
垂线是一条与已知直线垂直的直线;
垂直是两条直线之间的位置关系;
垂线段是一条与已知直线垂直的线段.
②联系:
垂线段所在的直线是已知直线的垂线;
垂线段所在的直线与已知直线垂直.
讲授新课
典例精析
【例3】过点P向线段AB所在直线引垂线,正确的是( )
A B C D
C
讲授新课
练一练
1.两条直线相交所成的四个角中,下列条件中能判定两条直线垂直的是( )
A. 有两个角相等 B.有两对角相等
C. 有三个角相等 D.有四对邻补角
C
当堂检测
如图,∠ABD = 90°,在下列各语句中填入适当的文字或数字:
(1)点 B 在直线______________上,点 D 在直线______外;
(2)直线_____与直线_____相交于点 A,点 D 是直线_____与直线_____的交点,也是直线_____与直线______的交点,又是直线_____与直线_____的交点;
(3)直线_____⊥直线______,垂足为点_____;
(4)过点 D 有且只有_____条直线与直线 AC 垂直.
AC(或BD)
AC
AD
AC
AD
BD
AD
CD
BD
CD
BD
AC
B
一
当堂检测
2. 如图,点P在直线AB上,点C,D在直线AB的上方,且PC⊥PD,∠APC=28°,则∠BPD的度数为( )
A. 28°
B. 60°
C. 62°
D. 152°
C
当堂检测
4. 如图,直线AB,CD相交于点O,若∠EOD=40°, ∠BOC=130°, 则射线OE与直线AB的位置关系是____________.
垂直
当堂检测
5.如图,是测量学生跳远成绩的示意图,即PA的长为某同学的跳远成绩,其依据是( )
A.两点之间线段最短 B.两点确定一条直线
C.垂线段最短 D.过一点有且只有一条直线与已知直线垂直
【答案】C
【分析】由点到直线的距离的定义及跳远比赛的规则作出判断.
【详解】解:能正确解释这一现象的数学知识是垂线段最短,
故选:C.
当堂检测
6.如图,AO⊥FD,OD为∠BOC的平分线,OE为射线OB的反向延长线,若∠AOB=40°,求∠EOF、∠COE的度数.
A
F
D
O
B
C
E
解:∵AO⊥OD且∠AOB=40°,
∴∠BOD=90°-40°=50°,
∴∠EOF=50°.
∵OD平分∠BOC,
∴∠DOC=∠BOD=50°,
∴∠COE=180°-50°-50°=80°.
当堂检测
7.如图,OA⊥OB,OC⊥OD,O是垂足,∠AOD=120°,那么∠COB的度数为______;
【详解】解:∵OA⊥OB,OC⊥OD,
∴∠AOB=90°
∵∠AOD=120°
∴∠BOD=120°-90°=30°
∠BOC=60°
故答案为:60°.
当堂检测
8.如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC:∠AOD=7:11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.
【答案】(1)145°
(2)125°
【点睛】本题考查的是邻补角的性质、对顶角的性质和角平分线的定义,垂直的定义,几何图形中角度的计算,掌握邻补角互补、对顶角相等和垂直的定义是解题的关键.
当堂检测
(1)
解:∵∠AOC:∠AOD=7:11,∠AOC+∠AOD=180°
∴∠AOC=????????????×????????????°=????????°,
∴∠DOB=∠AOC=70°,
又∵OE平分∠BOD,
∴∠DOE=????????∠????????????=????????×????????°=????????°,
∴∠COE=180°-∠DOE=180°-35°=145°,
(2)
∵OF⊥OE,
∴∠EOF=90°,
∴∠FOD=90°-∠DOE=90°-35°=55°,
∴∠COF=180°-∠FOD=180°-55°=125°.
?
课堂小结
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
1.垂线的定义
2.垂线的画法
3.垂线的性质
(1)过一点有且只有一条直线与已知直线垂直
一、放;二、靠;三、移 ;四、画.
4.点到直线的距离
(2)垂线段最短
谢 谢~
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
