25.2.2 用画树状图求概率 课件(共21张PPT)-2023-2024学年九年级数学上册同步精品课件(人教版)
文档属性
| 名称 | 25.2.2 用画树状图求概率 课件(共21张PPT)-2023-2024学年九年级数学上册同步精品课件(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 20:11:10 | ||
图片预览







文档简介
(共21张PPT)
第25章
概率初步
25.2.2用画树状图求概率
教学目标/Teaching aims
1
进一步理解等可能事件概率的意义.
2
掌握树状图法的定义,并能运用树状图计算事件的概率.
3
进一步学习分类思想方法,掌握有关数学技能.
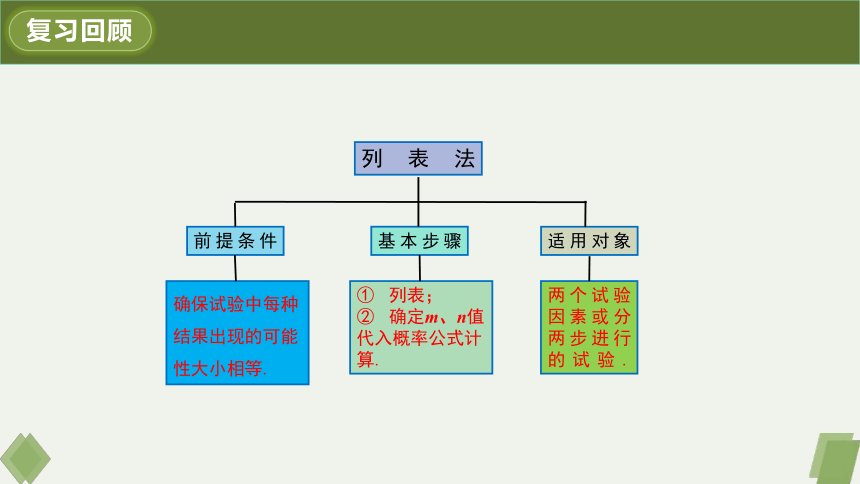
复习回顾
列表法
适用对象
两个试验因素或分两步进行的试验.
基本步骤
列表;
确定m、n值
代入概率公式计算.
确保试验中每种结果出现的可能性大小相等.
前提条件
新知探究
例、甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I。从3个口袋中各随机地取出1个小球。
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少?
(2)取出的3个小球上全是辅音字母的概率是多少?
本题中元音字母: A E I 辅音字母: B C D H
新知探究
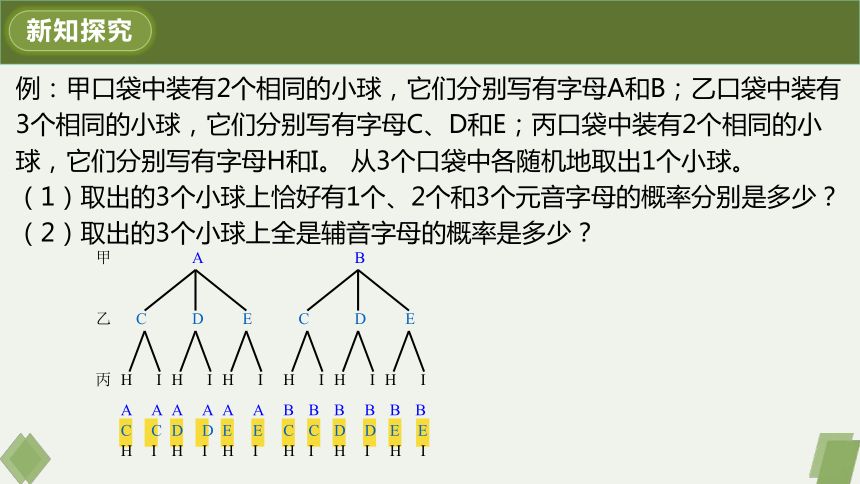
例:甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I。 从3个口袋中各随机地取出1个小球。
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少?
(2)取出的3个小球上全是辅音字母的概率是多少?
甲
乙
丙
A
C
D
E
H
I
H
I
H
I
B
C
D
E
H
I
H
I
H
I
B
C
H
A
C
H
A
C
I
A
D
H
A
D
I
A
E
H
A
E
I
B
C
I
B
D
H
B
D
I
B
E
H
B
E
I
新知探究
解:由树形图得,所有可能出现的结果有12个,它们出现的可能性相等。
(1)满足只有一个元音字母的结果有5个,则 P(一个元音)=
满足只有两个元音字母的结果有4个,则 P(两个元音)= =
满足三个全部为元音字母的结果有1个,则 P(三个元音)=
(2)满足全是辅音字母的结果有2个,则 P(三个辅音)= =
新知探究
想一想,什么时候用“列表法”方便,什么时候用“树形图”方便?
A
C
D
E
H
I
H
I
H
I
B
C
D
E
H
I
H
I
H
I
B
C
H
A
C
H
A
C
I
A
D
H
A
D
I
A
E
H
A
E
I
B
C
I
B
D
H
B
D
I
B
E
H
B
E
I
1 2 3 4 5 6
1 (1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
2 (1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
3 (1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
4 (1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
5 (1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
6 (1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
第
一
个
第
二
个
当一次试验涉及两个因素时,且可能出现的结果较多时,为不重复不遗漏地列出所有可能的结果,通常用列表法
当一次试验涉及3个因素或3个以上的因素时,列表法就不方便了,为不重复不遗漏地列出所有可能的结果,通常用树形图
归纳小结
树状图的画法
一个试验
第一个因素
第二个因素
如一个试验中涉及2个因素,第一个因素中有2种可能情况;第二个因素中有3种可能的情况.
A
B
1
2
3
1
2
3
则其树形图如下图:
n=2×3=6
树状图法:按事件发生的次序,列出事件可能出现的结果.
新知探究
用树状图法求概率的“四个步骤”:
1.定:确定该试验的几个步骤、顺序、每一步可能产生的结果.
2.画:列举每一环节可能产生的结果,得到树状图.
3.数:数出全部均等的结果数m和该事件出现的结果数n.
4.算:代入公式P(A)= .
巩固练习
同时抛掷三枚硬币,求下列事件的概率:
(1) 三枚硬币全部正面朝上;
(2) 两枚硬币正面朝上而一枚硬币反面朝上;
(3) 至少有两枚硬币正面朝上.
正
反
正
反
正
反
正
反
正
反
正
反
正
反
抛掷硬币试验
解:
由树形图可以看出,抛掷3枚硬币的结果有8种,它们出现的可能性相等.
∴ P(A)
(1)满足三枚硬币全部正面朝上(记为事件A)的结果只有1种
1
8
=
∴ P(B)
3
8
=
(2)满足两枚硬币正面朝上而一枚硬币反面朝上(记为事件B)的结果有3种
(3)满足至少有两枚硬币正面朝上(记为事件C)的结果有4种
∴ P(C)
4
8
=
1
2
=
第①枚
②
③
课堂练习
A
课堂练习
B
课堂练习
B
课堂练习
4.小贤同学总是不爱整理自己的物品,他的床头抽屉里放着2只白袜子和1只黑袜子,这些袜子除了颜色不同外没有任何区别,并且袜子在抽屉里是散开混在一起的.
(1)若小贤从抽屉里随机摸出一只袜子,则摸到白袜子的概率是______;
课堂练习
(2)若小贤从抽屉中随机一次性摸出两只袜子,请用列表法或画树状图法求小贤摸出的袜子恰好颜色相同的概率.
课堂练习
5.甲、乙、丙三个盒中分别装有大小、形状、质地相同的小球若干,甲盒中装有2个小球,分别写有字母A和B;乙盒中装有3个小球,分别写有字母C、D和E;丙盒中装有2个小球,分别写有字母H和I;现要从3个盒中各随机取出1个小球.
I
H
D
E
C
A
B
课堂练习
(1)取出的3个小球中恰好有1个,2个,3个写有元音字母的概率各是多少?
甲
乙
丙
A
C
D
E
H
I
H
I
H
I
B
C
D
E
H
I
H
I
H
I
B
C
H
A
C
H
A
C
I
A
D
H
A
D
I
A
E
H
A
E
I
B
C
I
B
D
H
B
D
I
B
E
H
B
E
I
解:由树状图得,所有可能出现的结果有12个,它们出现的可能性相等.
课堂练习
满足三个全部为元音字母的结果有1个,则
P(三个元音)=
满足只有两个元音字母的结果有4个,则 P(两个元音)= =
(1)满足只有一个元音字母的结果有5个,则
P(一个元音)=
课堂练习
(2)取出的3个小球上全是辅音字母的概率是多少?
甲
乙
丙
A
C
D
E
H
I
H
I
H
I
B
C
D
E
H
I
H
I
H
I
B
C
H
A
C
H
A
C
I
A
D
H
A
D
I
A
E
H
A
E
I
B
C
I
B
D
H
B
D
I
B
E
H
B
E
I
解:满足全是辅音字母的结果有2个,则
P(三个辅音)= = .
课堂总结
画树状图法求概率
步骤
定义
用树状图的形式反映事件发生的各种情况出现的次数和方法、以及某一事件发生的可能性次数和方式,并求出概率的方法.
适用条件:当一次试验涉及两个及其以上(通常3个)因素时,采用树状图法.
注意
③利用概率公式进行计算.
①关键要弄清楚每一步有几种结果;
②在树状图下面对应写着所有可能的结果;
在摸球试验一定要弄清“放回”还是“不放回”.(易错点)
25.2.2用画树状图求概率
谢谢观看
概率初步
第25章
概率初步
25.2.2用画树状图求概率
教学目标/Teaching aims
1
进一步理解等可能事件概率的意义.
2
掌握树状图法的定义,并能运用树状图计算事件的概率.
3
进一步学习分类思想方法,掌握有关数学技能.
复习回顾
列表法
适用对象
两个试验因素或分两步进行的试验.
基本步骤
列表;
确定m、n值
代入概率公式计算.
确保试验中每种结果出现的可能性大小相等.
前提条件
新知探究
例、甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I。从3个口袋中各随机地取出1个小球。
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少?
(2)取出的3个小球上全是辅音字母的概率是多少?
本题中元音字母: A E I 辅音字母: B C D H
新知探究
例:甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I。 从3个口袋中各随机地取出1个小球。
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少?
(2)取出的3个小球上全是辅音字母的概率是多少?
甲
乙
丙
A
C
D
E
H
I
H
I
H
I
B
C
D
E
H
I
H
I
H
I
B
C
H
A
C
H
A
C
I
A
D
H
A
D
I
A
E
H
A
E
I
B
C
I
B
D
H
B
D
I
B
E
H
B
E
I
新知探究
解:由树形图得,所有可能出现的结果有12个,它们出现的可能性相等。
(1)满足只有一个元音字母的结果有5个,则 P(一个元音)=
满足只有两个元音字母的结果有4个,则 P(两个元音)= =
满足三个全部为元音字母的结果有1个,则 P(三个元音)=
(2)满足全是辅音字母的结果有2个,则 P(三个辅音)= =
新知探究
想一想,什么时候用“列表法”方便,什么时候用“树形图”方便?
A
C
D
E
H
I
H
I
H
I
B
C
D
E
H
I
H
I
H
I
B
C
H
A
C
H
A
C
I
A
D
H
A
D
I
A
E
H
A
E
I
B
C
I
B
D
H
B
D
I
B
E
H
B
E
I
1 2 3 4 5 6
1 (1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
2 (1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
3 (1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
4 (1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
5 (1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
6 (1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
第
一
个
第
二
个
当一次试验涉及两个因素时,且可能出现的结果较多时,为不重复不遗漏地列出所有可能的结果,通常用列表法
当一次试验涉及3个因素或3个以上的因素时,列表法就不方便了,为不重复不遗漏地列出所有可能的结果,通常用树形图
归纳小结
树状图的画法
一个试验
第一个因素
第二个因素
如一个试验中涉及2个因素,第一个因素中有2种可能情况;第二个因素中有3种可能的情况.
A
B
1
2
3
1
2
3
则其树形图如下图:
n=2×3=6
树状图法:按事件发生的次序,列出事件可能出现的结果.
新知探究
用树状图法求概率的“四个步骤”:
1.定:确定该试验的几个步骤、顺序、每一步可能产生的结果.
2.画:列举每一环节可能产生的结果,得到树状图.
3.数:数出全部均等的结果数m和该事件出现的结果数n.
4.算:代入公式P(A)= .
巩固练习
同时抛掷三枚硬币,求下列事件的概率:
(1) 三枚硬币全部正面朝上;
(2) 两枚硬币正面朝上而一枚硬币反面朝上;
(3) 至少有两枚硬币正面朝上.
正
反
正
反
正
反
正
反
正
反
正
反
正
反
抛掷硬币试验
解:
由树形图可以看出,抛掷3枚硬币的结果有8种,它们出现的可能性相等.
∴ P(A)
(1)满足三枚硬币全部正面朝上(记为事件A)的结果只有1种
1
8
=
∴ P(B)
3
8
=
(2)满足两枚硬币正面朝上而一枚硬币反面朝上(记为事件B)的结果有3种
(3)满足至少有两枚硬币正面朝上(记为事件C)的结果有4种
∴ P(C)
4
8
=
1
2
=
第①枚
②
③
课堂练习
A
课堂练习
B
课堂练习
B
课堂练习
4.小贤同学总是不爱整理自己的物品,他的床头抽屉里放着2只白袜子和1只黑袜子,这些袜子除了颜色不同外没有任何区别,并且袜子在抽屉里是散开混在一起的.
(1)若小贤从抽屉里随机摸出一只袜子,则摸到白袜子的概率是______;
课堂练习
(2)若小贤从抽屉中随机一次性摸出两只袜子,请用列表法或画树状图法求小贤摸出的袜子恰好颜色相同的概率.
课堂练习
5.甲、乙、丙三个盒中分别装有大小、形状、质地相同的小球若干,甲盒中装有2个小球,分别写有字母A和B;乙盒中装有3个小球,分别写有字母C、D和E;丙盒中装有2个小球,分别写有字母H和I;现要从3个盒中各随机取出1个小球.
I
H
D
E
C
A
B
课堂练习
(1)取出的3个小球中恰好有1个,2个,3个写有元音字母的概率各是多少?
甲
乙
丙
A
C
D
E
H
I
H
I
H
I
B
C
D
E
H
I
H
I
H
I
B
C
H
A
C
H
A
C
I
A
D
H
A
D
I
A
E
H
A
E
I
B
C
I
B
D
H
B
D
I
B
E
H
B
E
I
解:由树状图得,所有可能出现的结果有12个,它们出现的可能性相等.
课堂练习
满足三个全部为元音字母的结果有1个,则
P(三个元音)=
满足只有两个元音字母的结果有4个,则 P(两个元音)= =
(1)满足只有一个元音字母的结果有5个,则
P(一个元音)=
课堂练习
(2)取出的3个小球上全是辅音字母的概率是多少?
甲
乙
丙
A
C
D
E
H
I
H
I
H
I
B
C
D
E
H
I
H
I
H
I
B
C
H
A
C
H
A
C
I
A
D
H
A
D
I
A
E
H
A
E
I
B
C
I
B
D
H
B
D
I
B
E
H
B
E
I
解:满足全是辅音字母的结果有2个,则
P(三个辅音)= = .
课堂总结
画树状图法求概率
步骤
定义
用树状图的形式反映事件发生的各种情况出现的次数和方法、以及某一事件发生的可能性次数和方式,并求出概率的方法.
适用条件:当一次试验涉及两个及其以上(通常3个)因素时,采用树状图法.
注意
③利用概率公式进行计算.
①关键要弄清楚每一步有几种结果;
②在树状图下面对应写着所有可能的结果;
在摸球试验一定要弄清“放回”还是“不放回”.(易错点)
25.2.2用画树状图求概率
谢谢观看
概率初步
同课章节目录
