河北省张家口市宣化区 2023-2024学年八年级人教版上学期期中数学试题(含答案)
文档属性
| 名称 | 河北省张家口市宣化区 2023-2024学年八年级人教版上学期期中数学试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 694.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 00:00:00 | ||
图片预览



文档简介
宣化区2023—2024学年度第一学期阶段性检测
八年级数学试卷(人教版)
(考试时间为90分钟,满分为100分)
一、选择题(本大题共12小题,每小题2分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
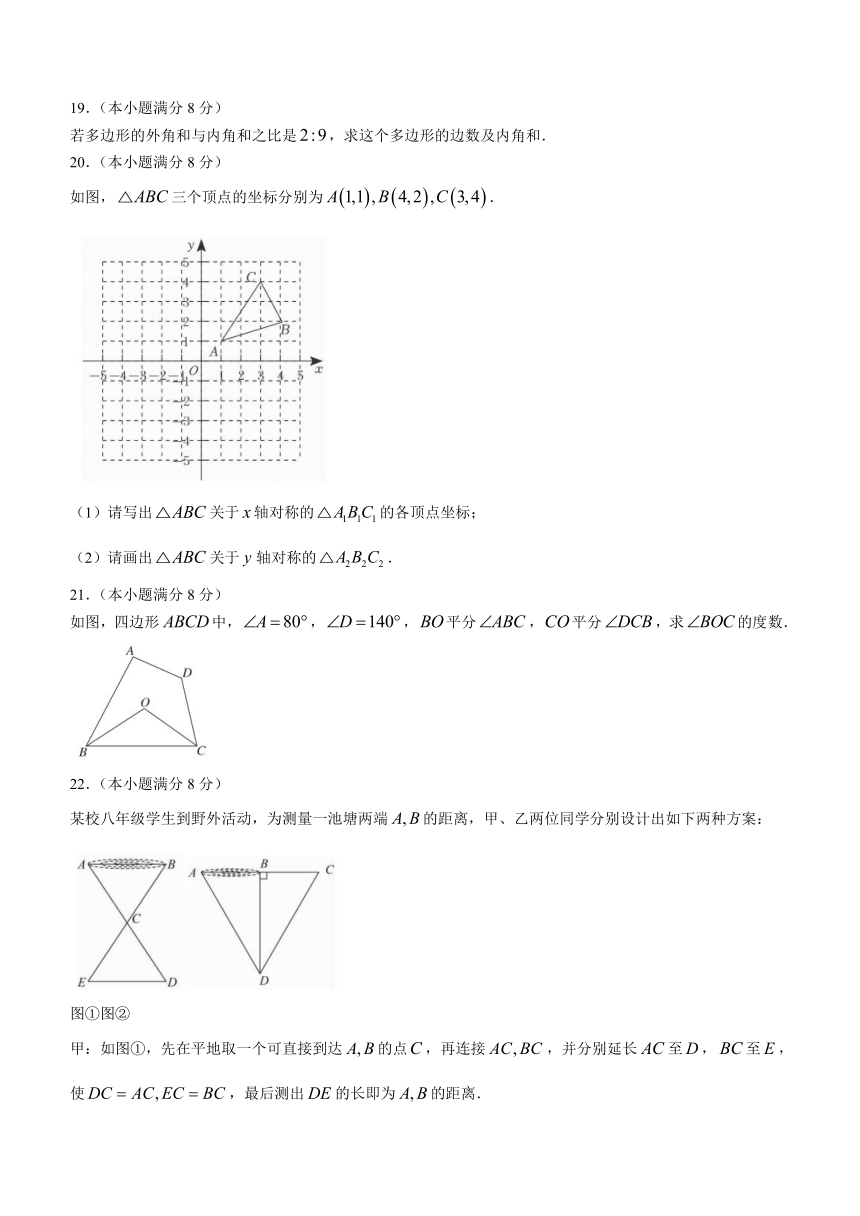
1.中华姓氏源于上古,每个姓氏都有自己的图腾.下列姓氏图腾是轴对称图形的是()
A. B. C. D.
2.已知线段,则下列长度的线段中,能与组成三角形的是()
A. B. C. D.
3.如图,是的高的是()
A. B.
C. D.
4.在中,沿图中虚线截去,则()
A. B. C. D.
5.如图,是两个全等三角形,图中的字母表示三角形的边长,则的度数为()
A. B. C. D.
6.一个多边形的内角和为,则这个多边形的边数为()
A.10 B.11 C.12 D.13
7.如图,在中,,是角平分线,,则到的距离是()
A.2 B.3 C.4 D.5
8.如图,是的外角,平分,平分,且交于点.若,则等于()
A. B. C. D.
9.点关于轴的对称点的坐标是()
A. B. C. D.
10.如图,已知于点于点,则图中全等的三角形共有()
第10题图
A.1对 B.2对 C.3对 D.4对
11.如图,在的正方形网格中有两个格点,连接,在网格中再找一个格点,使得是等腰三角形,满足条件的格点的个数是()
第11题图
A.5 B.6 C.8 D.9
12.如图,在等腰中,的平分线与的中垂线交于点,点沿折叠后与点重合,则的度数为()
第12题图
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分.把答案写在题中横线上)
13.在等腰中,顶角为,则为______.
14.若等腰三角形两边长分别为2和10,则它的周长是______.
15.若一个正多边形的一个内角是,则这是一个正______边形.
16.如图,自行车的车架上常常会焊接一条横梁,运用的数学原理是______.
第16题图
17.如图,已知,要使,只需添加的一个条件是______.
第17题图
18.如图,中,的角平分线交于点,延长,于,于,则下列结论:()
①平分;②;
③;④.
其中正确结论序号是______.
三、解答题(共7小题,共58分)
19.(本小题满分8分)
若多边形的外角和与内角和之比是,求这个多边形的边数及内角和.
20.(本小题满分8分)
如图,三个顶点的坐标分别为.
(1)请写出关于轴对称的的各顶点坐标;
(2)请画出关于轴对称的.
21.(本小题满分8分)
如图,四边形中,,,平分,平分,求的度数.
22.(本小题满分8分)
某校八年级学生到野外活动,为测量一池塘两端的距离,甲、乙两位同学分别设计出如下两种方案:
图①图②
甲:如图①,先在平地取一个可直接到达的点,再连接,并分别延长至,至,使,最后测出的长即为的距离.
乙:如图②,过点作,再由点观测,在的延长线上取一点,使,这时只要测出的长即为的距离.
(1)以上两位同学所设计的方案,可行的有______;
(2)请你选择一可行的方案,说说它可行的理由.
23.(本小题满分8分)
如图,在中,的垂直平分线分别交于点.
(1)若,求的度数;
(2)若,的周长为14,求的周长.
24.(本小题满分9分)
如图所示,在四边形中,,为的中点,连接,延长交的延长线于点.
(1)判断与的数量关系,并说明理由;
(2)若,则吗?为什么?
25.(本小题满分9分)
如图(1)所示,在一条直线上,,过分别作,,若.
(1)(2)
(1)试证明;
(2)若将的边沿方向移动,变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.
宣化区2023-2024学年度第一学期阶段性检测
八年级数学试卷参考答案及评分标准(人教版)
一、选择题(本大题有12个小题,每小题2分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A C B C D C A B A D C B
二、填空题(本大题共6小题,每小题3分,共18分.把答案写在题中横线上)
13.; 14.22; 15.八; 16.三角形的稳定性;
17.(答案不唯一); 18.①②③④.
三、解答题(本大题共7小题,共58分.解答应写出文字说明、证明过程或演算步骤)
19.解:①设这个多边形的内角和为度.
,解得
②设这个多边形是边形.
,解得
答:这个多边形是十一边形,内角和为.
20.解:(1).
(2)即为所求,图略.
21.解:,
平分,平分,
,
22.(1)甲、乙;
(2)解:选甲:在和中,
,
或选乙:,
,
在和中,,
.
23.解:(1),
,
是的垂直平分线,,
,
,
的度数为;
(2)是的垂直平分线,,
的周长为14,,
,,
,
的周长为22.
24.(1)解:结论:.
理由:,,
是的中点,,
在与中,
,;
(2)结论:.
理由:由(1)知,
,,
,即,
又,;
25.证明:图(1)中,,
.
.
在和中,,
,.
在和中,,
,.
图(2)中,结论依然成立.理由如下:
同图(1)得:,,
在和中,,
,.
八年级数学试卷(人教版)
(考试时间为90分钟,满分为100分)
一、选择题(本大题共12小题,每小题2分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.中华姓氏源于上古,每个姓氏都有自己的图腾.下列姓氏图腾是轴对称图形的是()
A. B. C. D.
2.已知线段,则下列长度的线段中,能与组成三角形的是()
A. B. C. D.
3.如图,是的高的是()
A. B.
C. D.
4.在中,沿图中虚线截去,则()
A. B. C. D.
5.如图,是两个全等三角形,图中的字母表示三角形的边长,则的度数为()
A. B. C. D.
6.一个多边形的内角和为,则这个多边形的边数为()
A.10 B.11 C.12 D.13
7.如图,在中,,是角平分线,,则到的距离是()
A.2 B.3 C.4 D.5
8.如图,是的外角,平分,平分,且交于点.若,则等于()
A. B. C. D.
9.点关于轴的对称点的坐标是()
A. B. C. D.
10.如图,已知于点于点,则图中全等的三角形共有()
第10题图
A.1对 B.2对 C.3对 D.4对
11.如图,在的正方形网格中有两个格点,连接,在网格中再找一个格点,使得是等腰三角形,满足条件的格点的个数是()
第11题图
A.5 B.6 C.8 D.9
12.如图,在等腰中,的平分线与的中垂线交于点,点沿折叠后与点重合,则的度数为()
第12题图
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分.把答案写在题中横线上)
13.在等腰中,顶角为,则为______.
14.若等腰三角形两边长分别为2和10,则它的周长是______.
15.若一个正多边形的一个内角是,则这是一个正______边形.
16.如图,自行车的车架上常常会焊接一条横梁,运用的数学原理是______.
第16题图
17.如图,已知,要使,只需添加的一个条件是______.
第17题图
18.如图,中,的角平分线交于点,延长,于,于,则下列结论:()
①平分;②;
③;④.
其中正确结论序号是______.
三、解答题(共7小题,共58分)
19.(本小题满分8分)
若多边形的外角和与内角和之比是,求这个多边形的边数及内角和.
20.(本小题满分8分)
如图,三个顶点的坐标分别为.
(1)请写出关于轴对称的的各顶点坐标;
(2)请画出关于轴对称的.
21.(本小题满分8分)
如图,四边形中,,,平分,平分,求的度数.
22.(本小题满分8分)
某校八年级学生到野外活动,为测量一池塘两端的距离,甲、乙两位同学分别设计出如下两种方案:
图①图②
甲:如图①,先在平地取一个可直接到达的点,再连接,并分别延长至,至,使,最后测出的长即为的距离.
乙:如图②,过点作,再由点观测,在的延长线上取一点,使,这时只要测出的长即为的距离.
(1)以上两位同学所设计的方案,可行的有______;
(2)请你选择一可行的方案,说说它可行的理由.
23.(本小题满分8分)
如图,在中,的垂直平分线分别交于点.
(1)若,求的度数;
(2)若,的周长为14,求的周长.
24.(本小题满分9分)
如图所示,在四边形中,,为的中点,连接,延长交的延长线于点.
(1)判断与的数量关系,并说明理由;
(2)若,则吗?为什么?
25.(本小题满分9分)
如图(1)所示,在一条直线上,,过分别作,,若.
(1)(2)
(1)试证明;
(2)若将的边沿方向移动,变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.
宣化区2023-2024学年度第一学期阶段性检测
八年级数学试卷参考答案及评分标准(人教版)
一、选择题(本大题有12个小题,每小题2分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A C B C D C A B A D C B
二、填空题(本大题共6小题,每小题3分,共18分.把答案写在题中横线上)
13.; 14.22; 15.八; 16.三角形的稳定性;
17.(答案不唯一); 18.①②③④.
三、解答题(本大题共7小题,共58分.解答应写出文字说明、证明过程或演算步骤)
19.解:①设这个多边形的内角和为度.
,解得
②设这个多边形是边形.
,解得
答:这个多边形是十一边形,内角和为.
20.解:(1).
(2)即为所求,图略.
21.解:,
平分,平分,
,
22.(1)甲、乙;
(2)解:选甲:在和中,
,
或选乙:,
,
在和中,,
.
23.解:(1),
,
是的垂直平分线,,
,
,
的度数为;
(2)是的垂直平分线,,
的周长为14,,
,,
,
的周长为22.
24.(1)解:结论:.
理由:,,
是的中点,,
在与中,
,;
(2)结论:.
理由:由(1)知,
,,
,即,
又,;
25.证明:图(1)中,,
.
.
在和中,,
,.
在和中,,
,.
图(2)中,结论依然成立.理由如下:
同图(1)得:,,
在和中,,
,.
同课章节目录
