数学人教A版(2019)必修第二册8.6.2直线与平面垂直的判定(共26张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册8.6.2直线与平面垂直的判定(共26张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 11:18:47 | ||
图片预览





文档简介
(共26张PPT)
直线与平面垂直的判定
复习引入
直线和平面的位置关系有几种
(1)直线在平面内(无数个公共点)
今天我们学习直线与平面相交的特殊情况:
直线与平面垂直
(2)直线与平面相交(有且只有一个公共点)
(3)直线与平面平行(没有公共点)
A
B
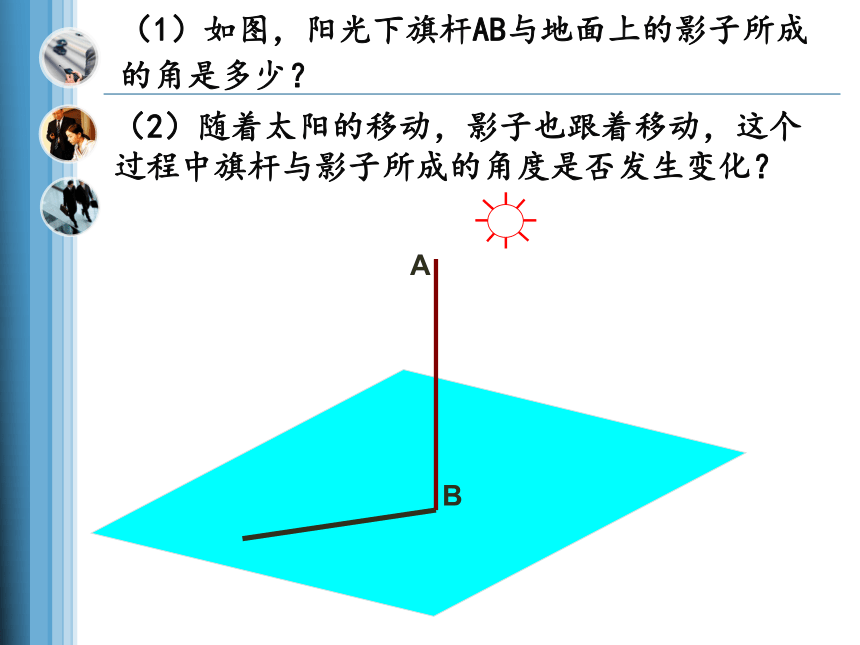
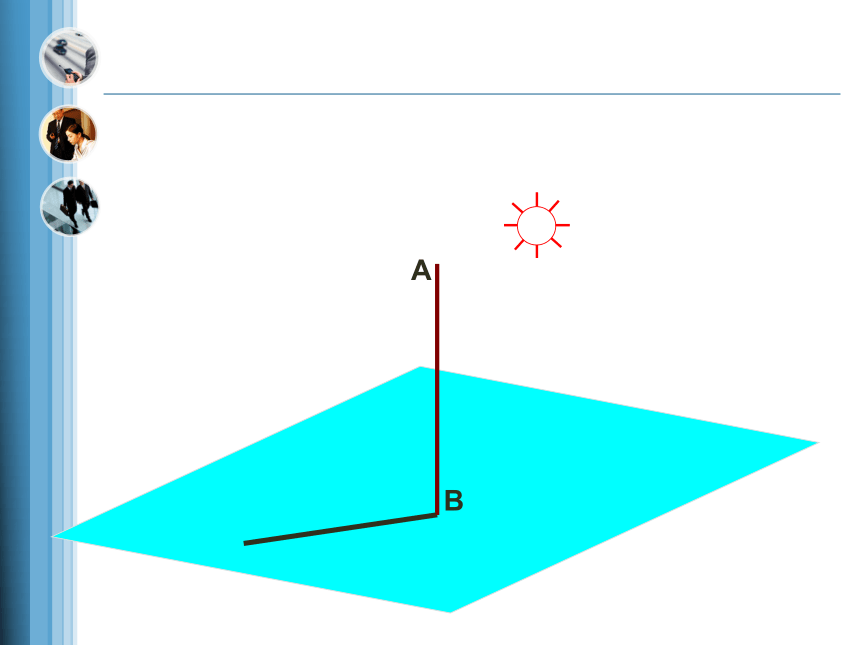
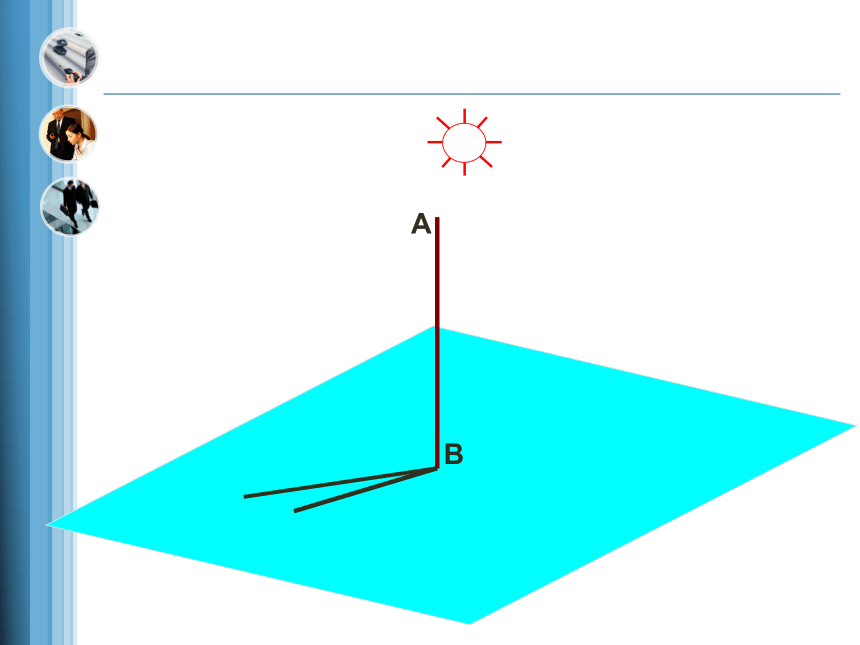
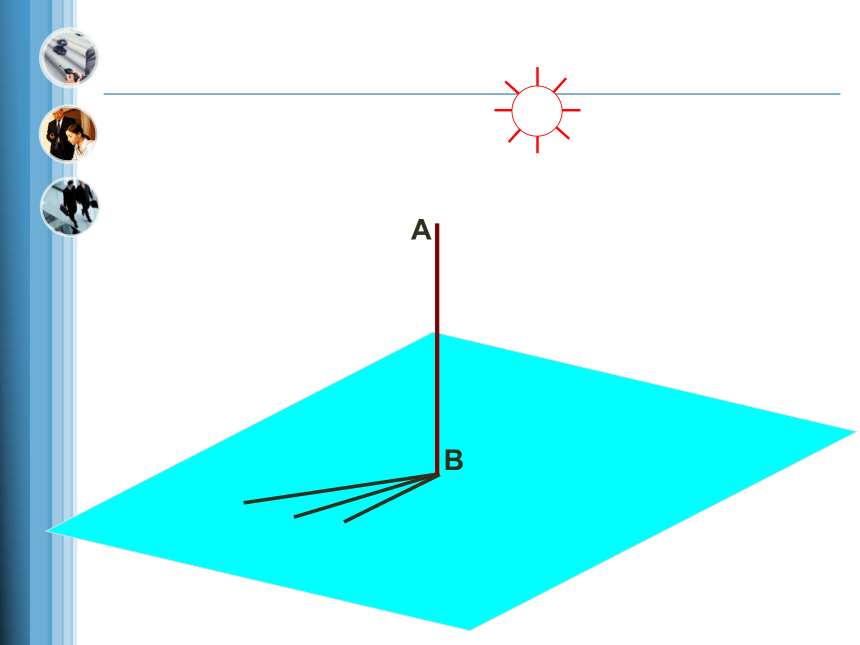
(1)如图,阳光下旗杆AB与地面上的影子所成的角是多少?
(2)随着太阳的移动,影子也跟着移动,这个过程中旗杆与影子所成的角度是否发生变化?
A
B
A
B
A
B
A
B
A
B
A
B
A
B
C
C1
B1
A
B
直线与平面垂直的定义:
如果直线
与平面
内的任意一条直线都
l
垂直,则称直线
l
和平面
互相垂直.
记作:
⊥
l
l
α
是平面α内任意一条直线
P
思考:(1)如果 ,那么 吗?
(2)定义中的“任意一条”能否换成“无数条”?
能否将定义中“任意一条”直线改为“无数条”直线?
实验要求:
1.将三角形纸片ABC 任意翻折,得到折痕AD;
2.将翻折后的纸片竖起放置在桌面上
(BD,CD与桌面接触)。
合作探究
问题1:折痕所在直线与桌面所在平面的位置关系如何?
问题2:如何翻折才能使折痕所在直线与桌面所在平面垂直?
操作确认 小心求证
合作探究
关键:折叠后,下面两条直线BD与BC边垂直!
归纳概括
判断直线与平面垂直的简单方法:
判定定理:一条直线与一个平面内两条相交直线都垂直,则该直线与此平面垂直。
符号语言
关键1:线不在多,相交则灵
关键2:线线垂直→线面垂直
例1 如图,在正方体 中
(1)请列举与平面ABCD垂直的直线;
(2)请列举与直线
垂直的平面.
例2 如图,在三棱锥S-ABC中,SA=SC,AB=BC,D是AC的中点.
求证:AC⊥平面SBD.
A
B
C
S
D
证明:
且D是AC的中点
AC⊥平面SBD
3、如图,在直三棱柱ABC A1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点.
求证:AD⊥平面A1DC1.
方法一:勾股定理证明垂直
AD⊥平面A1DC1
方法一:线面垂直 线线垂直
例3
如图,在直三棱柱ABC A1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点.
求证:AD⊥平面A1DC1.
AD⊥平面A1DC1
归纳小结
1.直线与平面垂直的定义
(1)利用定义:
(2)利用判定定理:
2.直线与平面垂直的判定
垂直于平面内任意一条直线
线面垂直
线线垂直
谢谢!
直线与平面垂直的判定
复习引入
直线和平面的位置关系有几种
(1)直线在平面内(无数个公共点)
今天我们学习直线与平面相交的特殊情况:
直线与平面垂直
(2)直线与平面相交(有且只有一个公共点)
(3)直线与平面平行(没有公共点)
A
B
(1)如图,阳光下旗杆AB与地面上的影子所成的角是多少?
(2)随着太阳的移动,影子也跟着移动,这个过程中旗杆与影子所成的角度是否发生变化?
A
B
A
B
A
B
A
B
A
B
A
B
A
B
C
C1
B1
A
B
直线与平面垂直的定义:
如果直线
与平面
内的任意一条直线都
l
垂直,则称直线
l
和平面
互相垂直.
记作:
⊥
l
l
α
是平面α内任意一条直线
P
思考:(1)如果 ,那么 吗?
(2)定义中的“任意一条”能否换成“无数条”?
能否将定义中“任意一条”直线改为“无数条”直线?
实验要求:
1.将三角形纸片ABC 任意翻折,得到折痕AD;
2.将翻折后的纸片竖起放置在桌面上
(BD,CD与桌面接触)。
合作探究
问题1:折痕所在直线与桌面所在平面的位置关系如何?
问题2:如何翻折才能使折痕所在直线与桌面所在平面垂直?
操作确认 小心求证
合作探究
关键:折叠后,下面两条直线BD与BC边垂直!
归纳概括
判断直线与平面垂直的简单方法:
判定定理:一条直线与一个平面内两条相交直线都垂直,则该直线与此平面垂直。
符号语言
关键1:线不在多,相交则灵
关键2:线线垂直→线面垂直
例1 如图,在正方体 中
(1)请列举与平面ABCD垂直的直线;
(2)请列举与直线
垂直的平面.
例2 如图,在三棱锥S-ABC中,SA=SC,AB=BC,D是AC的中点.
求证:AC⊥平面SBD.
A
B
C
S
D
证明:
且D是AC的中点
AC⊥平面SBD
3、如图,在直三棱柱ABC A1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点.
求证:AD⊥平面A1DC1.
方法一:勾股定理证明垂直
AD⊥平面A1DC1
方法一:线面垂直 线线垂直
例3
如图,在直三棱柱ABC A1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点.
求证:AD⊥平面A1DC1.
AD⊥平面A1DC1
归纳小结
1.直线与平面垂直的定义
(1)利用定义:
(2)利用判定定理:
2.直线与平面垂直的判定
垂直于平面内任意一条直线
线面垂直
线线垂直
谢谢!
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
