直线与平面平行
图片预览



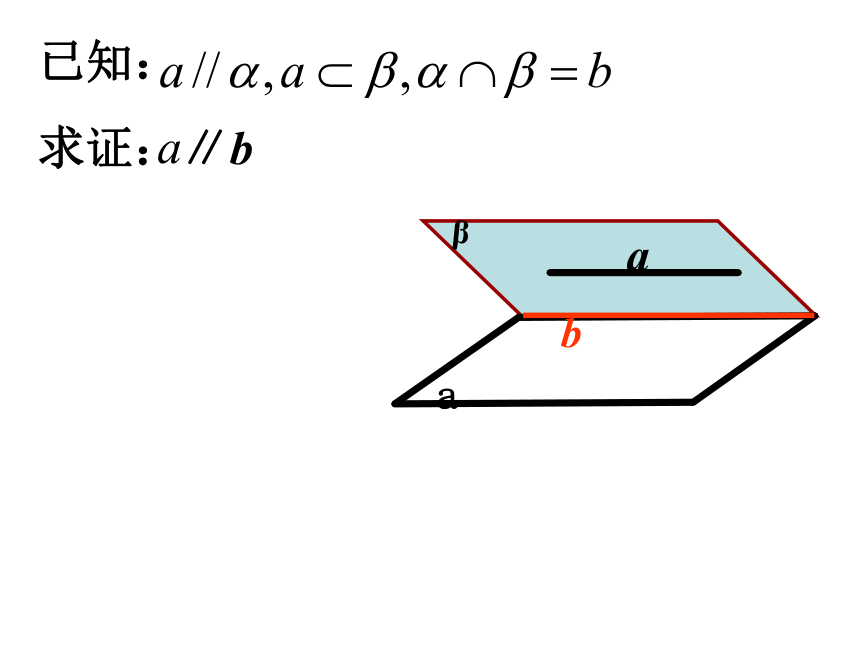



文档简介
课件24张PPT。直线和平面平行的性质定理(1)直线在平面内直线和平面相交或平行的情况统称为直线在平面外.1.直线和平面的位置关系一、复习(2)直线和平面相交(3)直线和平面平行直线与平面平行的判定定理:
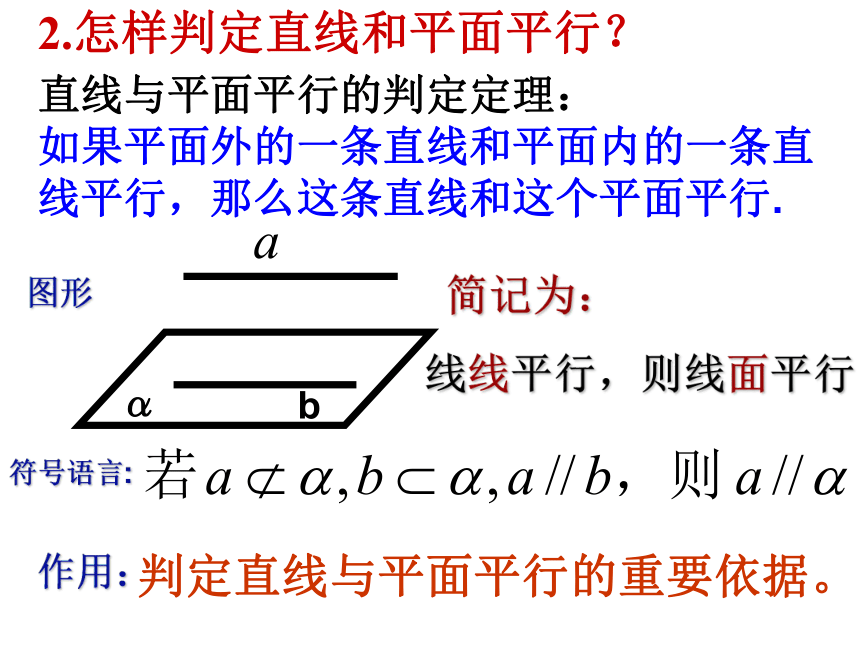
如果平面外的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行.简记为:线线平行,则线面平行。判定直线与平面平行的重要依据。图形作用:符号语言:2.怎样判定直线和平面平行? 3.如果一条直线和一个平面平行,那么这条直线和这个平面内的直线有怎样的位置关系? 4.已知直线 a∥平面α,如何在平面α内找出和直线 a平行的一条直线? βbβb符号语言:简记为:线面平行则线线平行作用1:可证明两直线平行。欲证“线线平行”,可先证明“线面平行”。直线和平面平行的性质定理
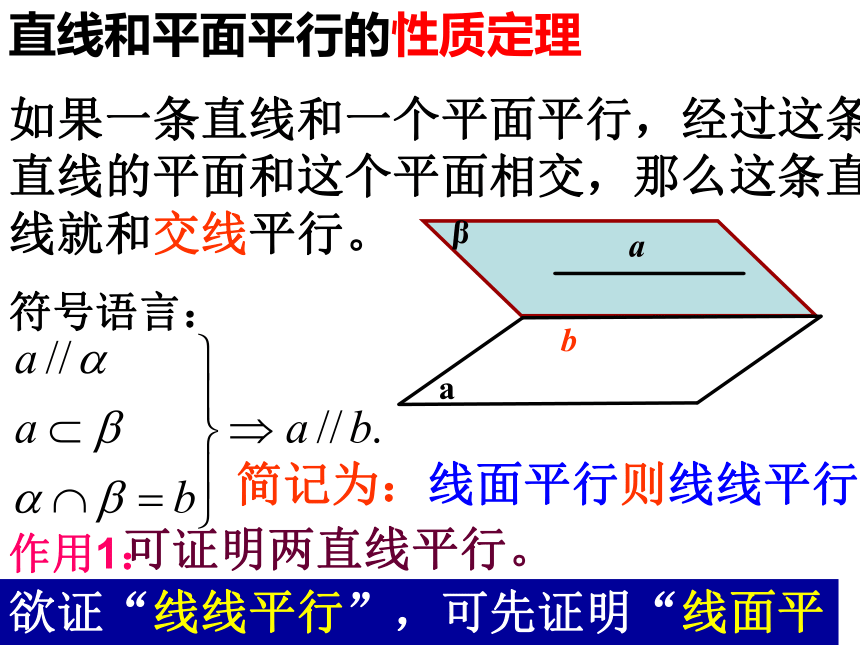
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。过直线做平面与已知平面相交,找出交线。已知直线 a∥平面α,如何在平面α内找出和直线 a 平行的一条直线? 作用2:给出了一种作平行线的重要方法.练习:(1).如果一条直线和一个平面平行, 这个平 面 内是否只有一条直线和已知直线平行呢? 平面内的哪些直线都和已知直线平行? 有多少条?(2).如果a∥α, 经过a 的一组平面分别和α相交于b、c、d …,b、c、d …是一组平行线吗?为什么? (4).过平面外一点与这平面平行的直线有多少条?(3).平行于同一平面的两条直线是否平行? 变式:点P在平面VAC中,过点P将木块锯开,使截面平行于直线VB和AC,应怎样画线?VABCPabcαβ 证明:过a 作平面β交平面α于直线 c ∵a∥α
∴a∥c
又 ∵a∥b
∴b∥c
∴b∥α. 例2、已知直线 a∥直线b,直线 a∥平面α, b α, 求证:b∥平面α变式:已知直线a ∥平面 ,直线a ∥平
面 ,分析: 利用公理4,寻求一条
直线分别与a,b均平行,从而
达到a∥b的目的.可借用已知
条件中的a∥α及a∥β来实现.说明:例5:例6. 已知ABCD是平行四边形,点P是平面ABCD外一点, M是 PC的中点,在 DM 上取一点G, 过 G 和AP作平面交平面BDM于GH,求证: AP // GH O练习:
(1)直线 a∥平面α,平面内α有 n 条互相平行的直线,那么这 n 条直线和直线 a ( )(A)全平行 (C)全平行或全异面
(B)全异面 (D)不全平行也不全异面
(2)直线 a∥平面α,平面α内有无数条直线 交于 一点,那么这无数条直线中与直线 a 平行的( )
(A)至少有一条 (B)至多有一条
(C)有且只有一条 (D)不可能有
CB 例8、在四面体ABCD中,E、F分别是AB、AC的中点,过直线EF作平面α,分别交BD、CD于M、N,求证:EF∥MN.证明的思路是线//线线//面如图,a,b是异面直线,O为AB的中点,过点O作平面?与两异面直线a,b都平行,MN交平面?于点P,求证:MP=PNabABOMNP?例9
如果平面外的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行.简记为:线线平行,则线面平行。判定直线与平面平行的重要依据。图形作用:符号语言:2.怎样判定直线和平面平行? 3.如果一条直线和一个平面平行,那么这条直线和这个平面内的直线有怎样的位置关系? 4.已知直线 a∥平面α,如何在平面α内找出和直线 a平行的一条直线? βbβb符号语言:简记为:线面平行则线线平行作用1:可证明两直线平行。欲证“线线平行”,可先证明“线面平行”。直线和平面平行的性质定理
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。过直线做平面与已知平面相交,找出交线。已知直线 a∥平面α,如何在平面α内找出和直线 a 平行的一条直线? 作用2:给出了一种作平行线的重要方法.练习:(1).如果一条直线和一个平面平行, 这个平 面 内是否只有一条直线和已知直线平行呢? 平面内的哪些直线都和已知直线平行? 有多少条?(2).如果a∥α, 经过a 的一组平面分别和α相交于b、c、d …,b、c、d …是一组平行线吗?为什么? (4).过平面外一点与这平面平行的直线有多少条?(3).平行于同一平面的两条直线是否平行? 变式:点P在平面VAC中,过点P将木块锯开,使截面平行于直线VB和AC,应怎样画线?VABCPabcαβ 证明:过a 作平面β交平面α于直线 c ∵a∥α
∴a∥c
又 ∵a∥b
∴b∥c
∴b∥α. 例2、已知直线 a∥直线b,直线 a∥平面α, b α, 求证:b∥平面α变式:已知直线a ∥平面 ,直线a ∥平
面 ,分析: 利用公理4,寻求一条
直线分别与a,b均平行,从而
达到a∥b的目的.可借用已知
条件中的a∥α及a∥β来实现.说明:例5:例6. 已知ABCD是平行四边形,点P是平面ABCD外一点, M是 PC的中点,在 DM 上取一点G, 过 G 和AP作平面交平面BDM于GH,求证: AP // GH O练习:
(1)直线 a∥平面α,平面内α有 n 条互相平行的直线,那么这 n 条直线和直线 a ( )(A)全平行 (C)全平行或全异面
(B)全异面 (D)不全平行也不全异面
(2)直线 a∥平面α,平面α内有无数条直线 交于 一点,那么这无数条直线中与直线 a 平行的( )
(A)至少有一条 (B)至多有一条
(C)有且只有一条 (D)不可能有
CB 例8、在四面体ABCD中,E、F分别是AB、AC的中点,过直线EF作平面α,分别交BD、CD于M、N,求证:EF∥MN.证明的思路是线//线线//面如图,a,b是异面直线,O为AB的中点,过点O作平面?与两异面直线a,b都平行,MN交平面?于点P,求证:MP=PNabABOMNP?例9
