23.2 解直角三角形及其应用分层练习(含答案)
文档属性
| 名称 | 23.2 解直角三角形及其应用分层练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 749.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 07:01:39 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
23.2解直角三角形及其应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,某地修建高速公路,要从B地向C地修一条隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升300米到达A处,在A处观察B地的俯角为,则B,C两地之间的距离为( )
A.米 B.米 C.米 D.米
2.在三角形ABC中,C为直角,sinA=,则tanB的值为( ).
A. B. C. D.
3.如图,从航拍无人机看一栋楼顶部的仰角为,看这栋楼底部的俯角为,无人机与楼的水平距离为,则这栋楼的高度为( )
A. B. C. D.
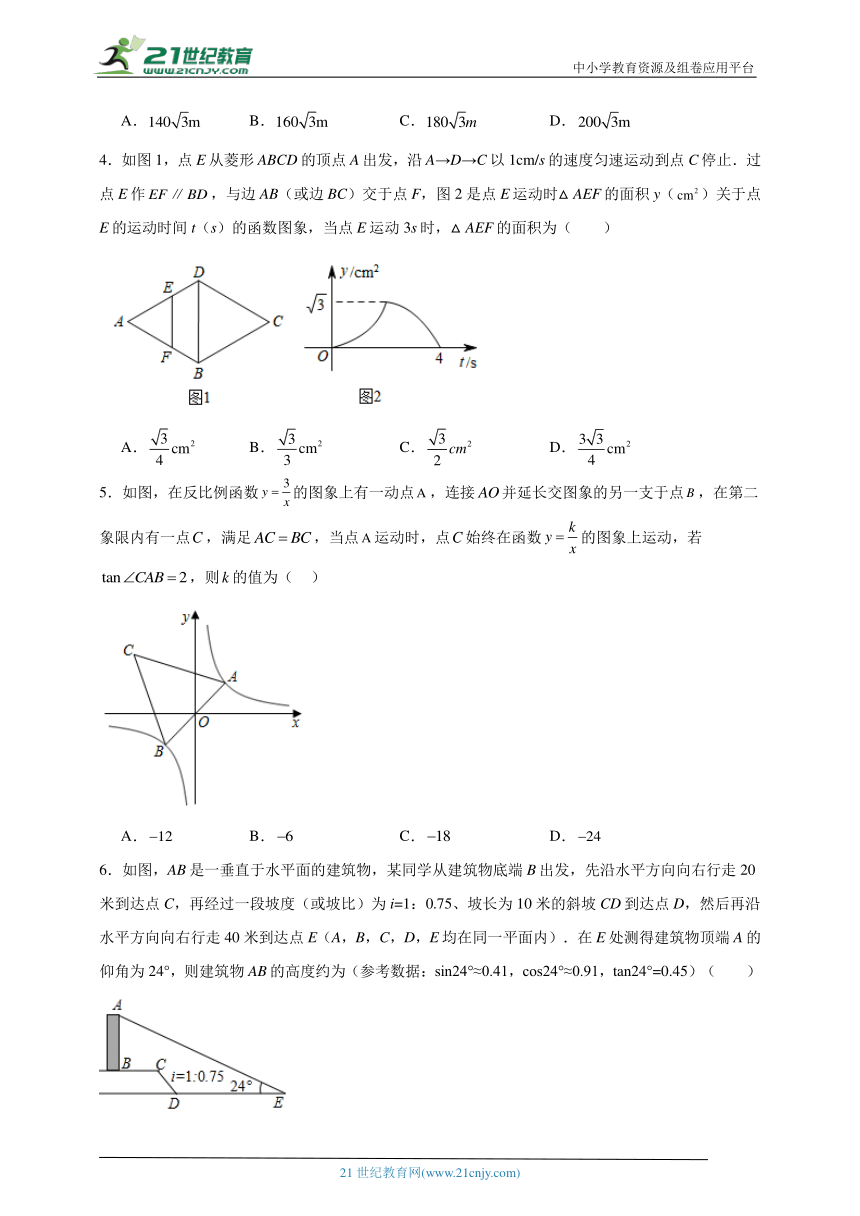
4.如图1,点E从菱形ABCD的顶点A出发,沿A→D→C以1cm/s的速度匀速运动到点C停止.过点E作,与边AB(或边BC)交于点F,图2是点E运动时△AEF的面积y()关于点E的运动时间t(s)的函数图象,当点E运动3s时,△AEF的面积为( )
A. B. C. D.
5.如图,在反比例函数的图象上有一动点,连接并延长交图象的另一支于点,在第二象限内有一点,满足,当点运动时,点始终在函数的图象上运动,若,则的值为( )
A. B. C. D.
6.如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )
A.21.7米 B.22.4米 C.27.4米 D.28.8米
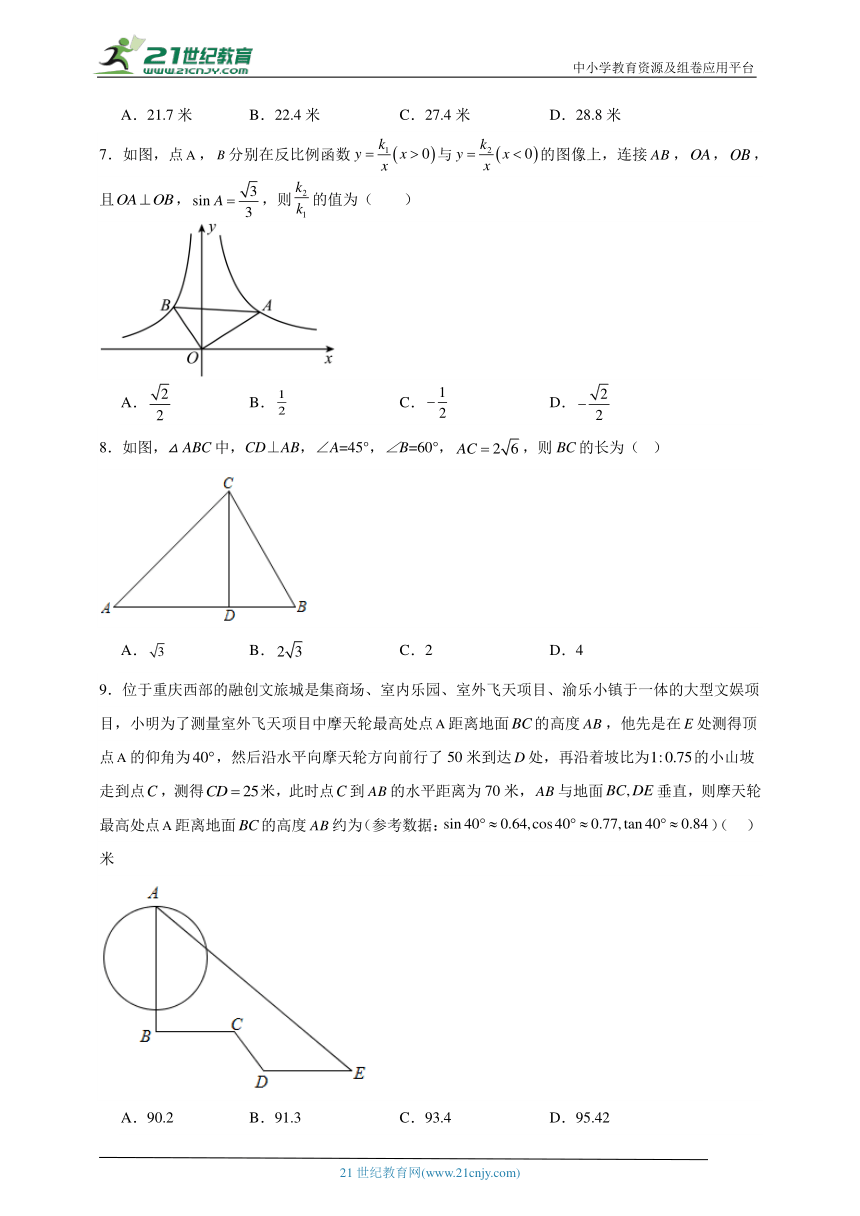
7.如图,点,分别在反比例函数与的图像上,连接,,,且,,则的值为( )
A. B. C. D.
8.如图,△ABC中,CD⊥AB,∠A=45°,∠B=60°,,则BC的长为( )
A. B. C.2 D.4
9.位于重庆西部的融创文旅城是集商场、室内乐园、室外飞天项目、渝乐小镇于一体的大型文娱项目,小明为了测量室外飞天项目中摩天轮最高处点距离地面的高度,他先是在处测得顶点的仰角为,然后沿水平向摩天轮方向前行了50米到达处,再沿着坡比为的小山坡走到点,测得米,此时点到的水平距离为70米,与地面垂直,则摩天轮最高处点距离地面的高度约为(参考数据:)( )米
A.90.2 B.91.3 C.93.4 D.95.42
10.小明身高1.5米,在操场的影长为2米,同时测得教学大楼在操场的影长为60米,则教学大楼的高度应为( )
A.45米 B.40米 C.90米 D.80米
二、填空题
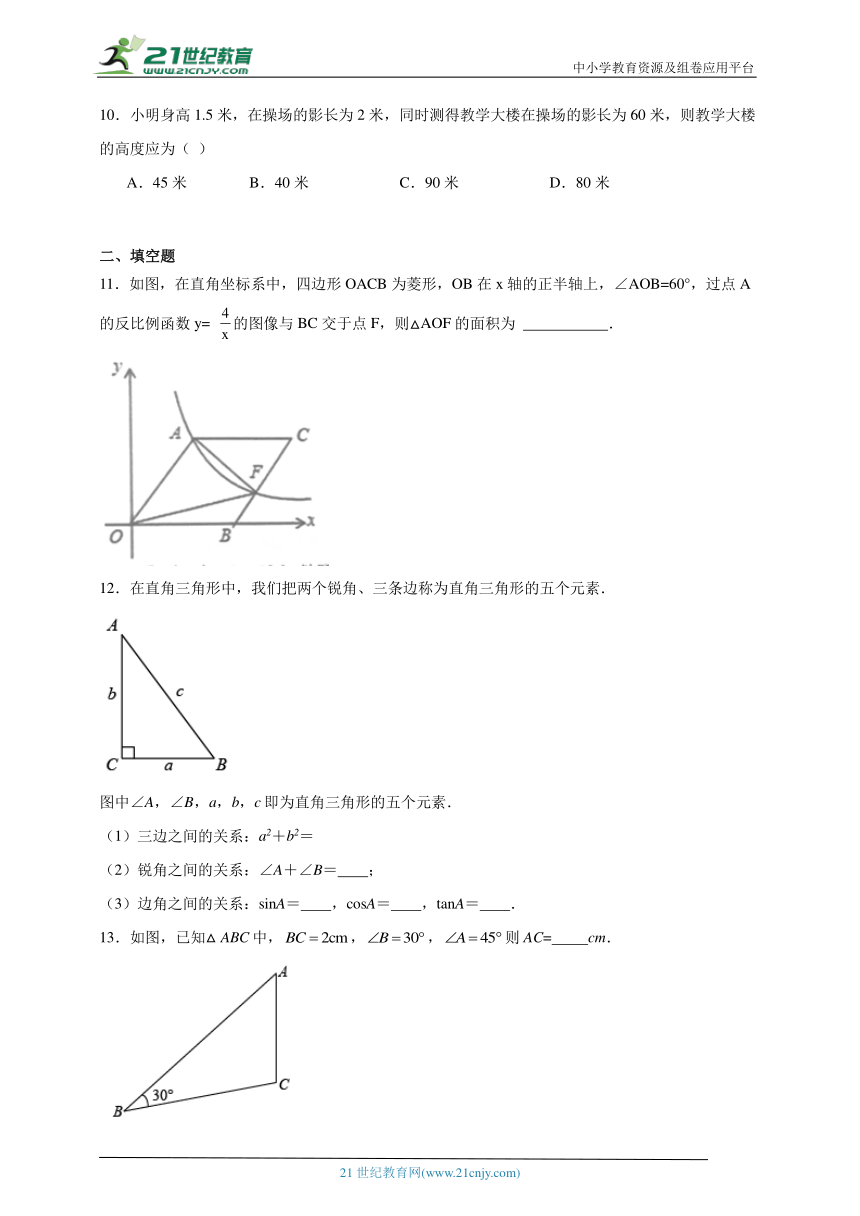
11.如图,在直角坐标系中,四边形OACB为菱形,OB在x轴的正半轴上,∠AOB=60°,过点A的反比例函数y= 的图像与BC交于点F,则△AOF的面积为 .
12.在直角三角形中,我们把两个锐角、三条边称为直角三角形的五个元素.
图中∠A,∠B,a,b,c即为直角三角形的五个元素.
(1)三边之间的关系:a2+b2=
(2)锐角之间的关系:∠A+∠B= ;
(3)边角之间的关系:sinA= ,cosA= ,tanA= .
13.如图,已知△ABC中,,,则AC= cm.
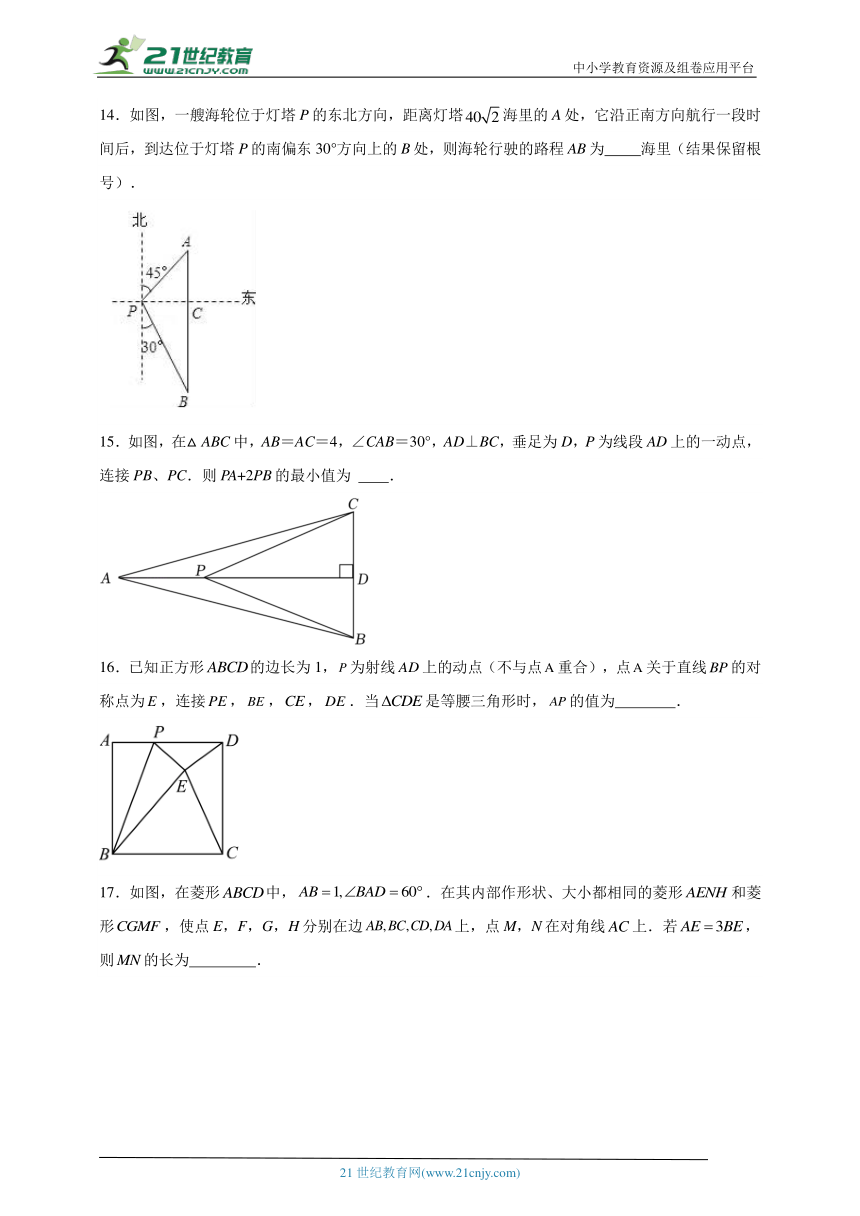
14.如图,一艘海轮位于灯塔P的东北方向,距离灯塔海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为 海里(结果保留根号).
15.如图,在△ABC中,AB=AC=4,∠CAB=30°,AD⊥BC,垂足为D,P为线段AD上的一动点,连接PB、PC.则PA+2PB的最小值为 .
16.已知正方形的边长为1,为射线上的动点(不与点重合),点关于直线的对称点为,连接,,,.当是等腰三角形时,的值为 .
17.如图,在菱形中,.在其内部作形状、大小都相同的菱形和菱形,使点E,F,G,H分别在边上,点M,N在对角线上.若,则的长为 .
18.小明沿着坡度i为1∶的直路向上走了50 m,则小明沿垂直方向升高了 m.
19.如图1,一扇窗户打开一定角度,其中一端固定在窗户边OM上的点A处,另一端B在边ON上滑动,图2为某一位置从上往下看的平面图,测得∠ABO为30°,∠AOB为45°,OB长为()厘米,则AB的长为 厘米.
20.在△ABC中,AC=6 ,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为 ,并且CD⊥AC,则BC的长为 .
三、解答题
21.习近平总书记指出“没有全民健康,就没有全面小康”,全民健身被越来越多的人接纳,人们的健身方式更加多元,健身场地更加丰富,沿河跑步也成为一种时尚.九年级学生小明在河边跑步时,决定用数学知识计算河的宽度,如图是一条河的示意图,小明沿河岸跑步,对岸EF上有两棵大树A,B,当小明跑到C处时,测得大树A在北偏东方向,小明继续跑步5分钟到达D处,此时大树B刚好在北偏西方向,已知,,小明跑步的平均速度是每分钟,请根据以上数据求出该段河的宽度.(结果精确到.参考数据:,,,)
22.
(1)如图1,在菱形ABCD中,E,F分别是AB和BC上的点,且BE=BF,则DE与DF之间的数量关系是 .
(2)[变式感知]在菱形ABCD中,∠A=60°,∠EDF的两边DE,DF分别交菱形的边AB,BC于点E,F.如图2,当∠EDF=60°时.
①AE+CF AD;(填“<”、“>”或“=”)
②如图3,若DE=4,AE=CF,求AB的长.
(3)[拓展应用]如图4,当∠EDF=90°时,若AB=60,AE+CF=32,求△DEF的面积.
23.在数学活动课上,老师带领学生测河宽.如图,在河岸边找到合适的观测地(平行于河流方向),河对岸一观测点,并测得米,,.求河的宽.(结果保留根号)
24.根据下列条件,求出Rt△ABC(∠C=90°)中未知的边和锐角.
(1)BC=8,∠B=60°.
(2)∠B=45°,AC=.
25.综合与实践
数学是以数量关系和空间形式为主要研究对象的科学.数学实践活动有利于我们在图形运动变化的过程中去发现其中的位置关系和数量关系,让我们在学习与探索中发现数学的美,体会数学实践活动带给我们的乐趣.
如图①,在矩形ABCD中,点E、F、G分别为边BC、AB、AD的中点,连接EF、DF,H为DF的中点,连接GH.将△BEF绕点B旋转,线段DF、GH和CE的位置和长度也随之变化.当△BEF绕点B顺时针旋转90°时,请解决下列问题:
(1)图②中,AB=BC,此时点E落在AB的延长线上,点F落在线段BC上,连接AF,猜想GH与CE之间的数量关系,并证明你的猜想;
(2)图③中,AB=2,BC=3,则 ;
(3)当AB=m , BC=n时. .
(4)在(2)的条件下,连接图③中矩形的对角线AC,并沿对角线AC剪开,得△ABC(如图④).点M、N分别在AC、BC上,连接MN,将△CMN沿 MN翻折,使点C的对应点P落在AB的延长线上,若PM平分∠APN,则CM长为 .
参考答案:
1.C
2.C
3.B
4.D
5.A
6.A
7.C
8.D
9.C
10.A
11.4
12. c2 90°
13.
14.
15.4
16.或或
17./
18.25
19.32
20. 或15
21.该段河的宽度约是.
22.(1)DE=DF
(2)①=;②
(3)840
23.米
24.(1)∠A=30° AB=16 AC=8;(2)∠A=45° BC= AB=2.
25.(1)
(2)
(3)
(4)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
23.2解直角三角形及其应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,某地修建高速公路,要从B地向C地修一条隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升300米到达A处,在A处观察B地的俯角为,则B,C两地之间的距离为( )
A.米 B.米 C.米 D.米
2.在三角形ABC中,C为直角,sinA=,则tanB的值为( ).
A. B. C. D.
3.如图,从航拍无人机看一栋楼顶部的仰角为,看这栋楼底部的俯角为,无人机与楼的水平距离为,则这栋楼的高度为( )
A. B. C. D.
4.如图1,点E从菱形ABCD的顶点A出发,沿A→D→C以1cm/s的速度匀速运动到点C停止.过点E作,与边AB(或边BC)交于点F,图2是点E运动时△AEF的面积y()关于点E的运动时间t(s)的函数图象,当点E运动3s时,△AEF的面积为( )
A. B. C. D.
5.如图,在反比例函数的图象上有一动点,连接并延长交图象的另一支于点,在第二象限内有一点,满足,当点运动时,点始终在函数的图象上运动,若,则的值为( )
A. B. C. D.
6.如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )
A.21.7米 B.22.4米 C.27.4米 D.28.8米
7.如图,点,分别在反比例函数与的图像上,连接,,,且,,则的值为( )
A. B. C. D.
8.如图,△ABC中,CD⊥AB,∠A=45°,∠B=60°,,则BC的长为( )
A. B. C.2 D.4
9.位于重庆西部的融创文旅城是集商场、室内乐园、室外飞天项目、渝乐小镇于一体的大型文娱项目,小明为了测量室外飞天项目中摩天轮最高处点距离地面的高度,他先是在处测得顶点的仰角为,然后沿水平向摩天轮方向前行了50米到达处,再沿着坡比为的小山坡走到点,测得米,此时点到的水平距离为70米,与地面垂直,则摩天轮最高处点距离地面的高度约为(参考数据:)( )米
A.90.2 B.91.3 C.93.4 D.95.42
10.小明身高1.5米,在操场的影长为2米,同时测得教学大楼在操场的影长为60米,则教学大楼的高度应为( )
A.45米 B.40米 C.90米 D.80米
二、填空题
11.如图,在直角坐标系中,四边形OACB为菱形,OB在x轴的正半轴上,∠AOB=60°,过点A的反比例函数y= 的图像与BC交于点F,则△AOF的面积为 .
12.在直角三角形中,我们把两个锐角、三条边称为直角三角形的五个元素.
图中∠A,∠B,a,b,c即为直角三角形的五个元素.
(1)三边之间的关系:a2+b2=
(2)锐角之间的关系:∠A+∠B= ;
(3)边角之间的关系:sinA= ,cosA= ,tanA= .
13.如图,已知△ABC中,,,则AC= cm.
14.如图,一艘海轮位于灯塔P的东北方向,距离灯塔海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为 海里(结果保留根号).
15.如图,在△ABC中,AB=AC=4,∠CAB=30°,AD⊥BC,垂足为D,P为线段AD上的一动点,连接PB、PC.则PA+2PB的最小值为 .
16.已知正方形的边长为1,为射线上的动点(不与点重合),点关于直线的对称点为,连接,,,.当是等腰三角形时,的值为 .
17.如图,在菱形中,.在其内部作形状、大小都相同的菱形和菱形,使点E,F,G,H分别在边上,点M,N在对角线上.若,则的长为 .
18.小明沿着坡度i为1∶的直路向上走了50 m,则小明沿垂直方向升高了 m.
19.如图1,一扇窗户打开一定角度,其中一端固定在窗户边OM上的点A处,另一端B在边ON上滑动,图2为某一位置从上往下看的平面图,测得∠ABO为30°,∠AOB为45°,OB长为()厘米,则AB的长为 厘米.
20.在△ABC中,AC=6 ,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为 ,并且CD⊥AC,则BC的长为 .
三、解答题
21.习近平总书记指出“没有全民健康,就没有全面小康”,全民健身被越来越多的人接纳,人们的健身方式更加多元,健身场地更加丰富,沿河跑步也成为一种时尚.九年级学生小明在河边跑步时,决定用数学知识计算河的宽度,如图是一条河的示意图,小明沿河岸跑步,对岸EF上有两棵大树A,B,当小明跑到C处时,测得大树A在北偏东方向,小明继续跑步5分钟到达D处,此时大树B刚好在北偏西方向,已知,,小明跑步的平均速度是每分钟,请根据以上数据求出该段河的宽度.(结果精确到.参考数据:,,,)
22.
(1)如图1,在菱形ABCD中,E,F分别是AB和BC上的点,且BE=BF,则DE与DF之间的数量关系是 .
(2)[变式感知]在菱形ABCD中,∠A=60°,∠EDF的两边DE,DF分别交菱形的边AB,BC于点E,F.如图2,当∠EDF=60°时.
①AE+CF AD;(填“<”、“>”或“=”)
②如图3,若DE=4,AE=CF,求AB的长.
(3)[拓展应用]如图4,当∠EDF=90°时,若AB=60,AE+CF=32,求△DEF的面积.
23.在数学活动课上,老师带领学生测河宽.如图,在河岸边找到合适的观测地(平行于河流方向),河对岸一观测点,并测得米,,.求河的宽.(结果保留根号)
24.根据下列条件,求出Rt△ABC(∠C=90°)中未知的边和锐角.
(1)BC=8,∠B=60°.
(2)∠B=45°,AC=.
25.综合与实践
数学是以数量关系和空间形式为主要研究对象的科学.数学实践活动有利于我们在图形运动变化的过程中去发现其中的位置关系和数量关系,让我们在学习与探索中发现数学的美,体会数学实践活动带给我们的乐趣.
如图①,在矩形ABCD中,点E、F、G分别为边BC、AB、AD的中点,连接EF、DF,H为DF的中点,连接GH.将△BEF绕点B旋转,线段DF、GH和CE的位置和长度也随之变化.当△BEF绕点B顺时针旋转90°时,请解决下列问题:
(1)图②中,AB=BC,此时点E落在AB的延长线上,点F落在线段BC上,连接AF,猜想GH与CE之间的数量关系,并证明你的猜想;
(2)图③中,AB=2,BC=3,则 ;
(3)当AB=m , BC=n时. .
(4)在(2)的条件下,连接图③中矩形的对角线AC,并沿对角线AC剪开,得△ABC(如图④).点M、N分别在AC、BC上,连接MN,将△CMN沿 MN翻折,使点C的对应点P落在AB的延长线上,若PM平分∠APN,则CM长为 .
参考答案:
1.C
2.C
3.B
4.D
5.A
6.A
7.C
8.D
9.C
10.A
11.4
12. c2 90°
13.
14.
15.4
16.或或
17./
18.25
19.32
20. 或15
21.该段河的宽度约是.
22.(1)DE=DF
(2)①=;②
(3)840
23.米
24.(1)∠A=30° AB=16 AC=8;(2)∠A=45° BC= AB=2.
25.(1)
(2)
(3)
(4)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
