22.3 相似三角形的性质分层练习(含答案)
文档属性
| 名称 | 22.3 相似三角形的性质分层练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 716.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 08:12:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
22.3相似三角形的性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
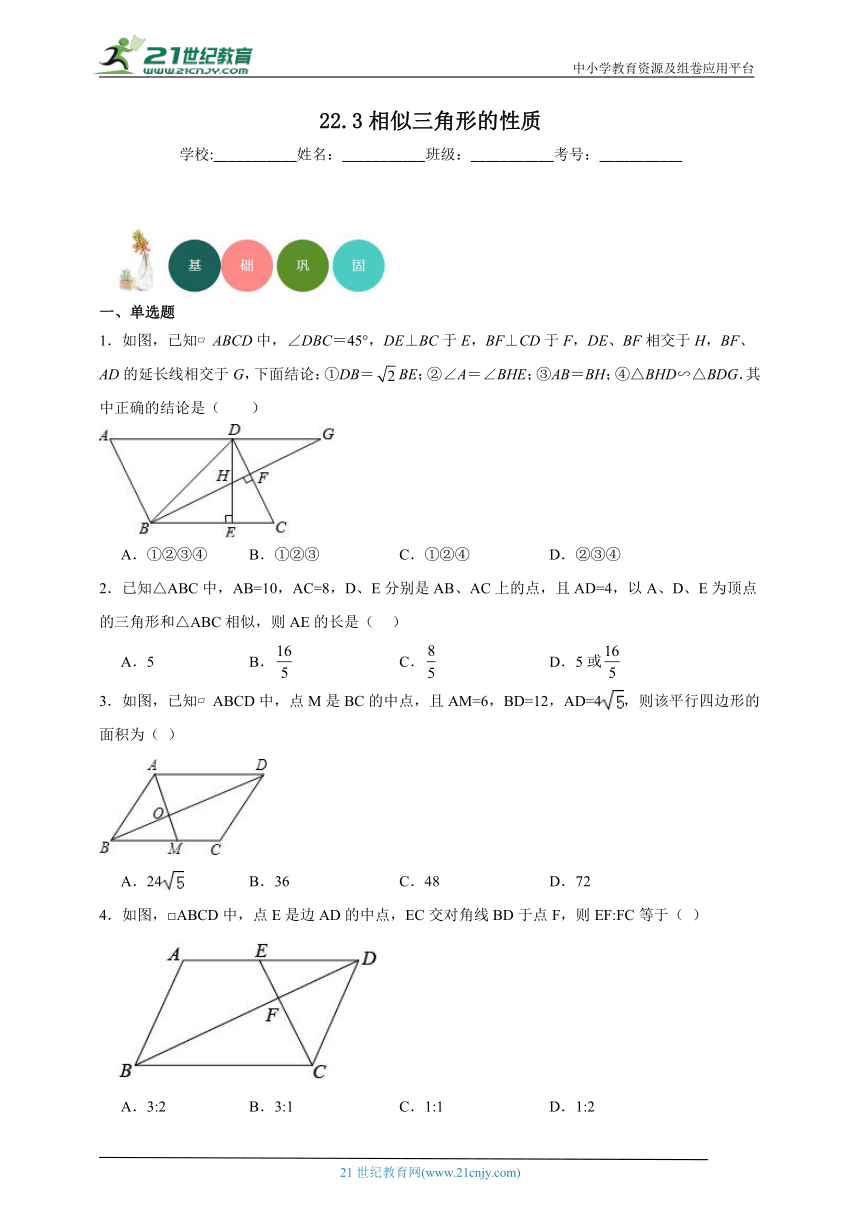
1.如图,已知 ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:①DB=BE;②∠A=∠BHE;③AB=BH;④△BHD∽△BDG.其中正确的结论是( )
A.①②③④ B.①②③ C.①②④ D.②③④
2.已知△ABC中,AB=10,AC=8,D、E分别是AB、AC上的点,且AD=4,以A、D、E为顶点的三角形和△ABC相似,则AE的长是( )
A.5 B. C. D.5或
3.如图,已知 ABCD中,点M是BC的中点,且AM=6,BD=12,AD=4,则该平行四边形的面积为( )
A.24 B.36 C.48 D.72
4.如图,□ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
A.3:2 B.3:1 C.1:1 D.1:2
5.如图,中,点,分别在,上,,若,,则与的面积之比为( )
A. B. C. D.
6.如图,正方形中,点分别在上,是等边三角形,连接交于点,过点作于点,若,则下列结论:①;②;③;④⑤其中结论正确的个数有( )
A.2个 B.3个 C.4个 D.5个
7.由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.点,分别为,的中点,若PQ恰好经过点F,则的值为( )
A. B.3 C. D.4
8.如图,中,,,,则与的相似比是( )
A.3:2 B.2:3 C.3:5 D.5:3
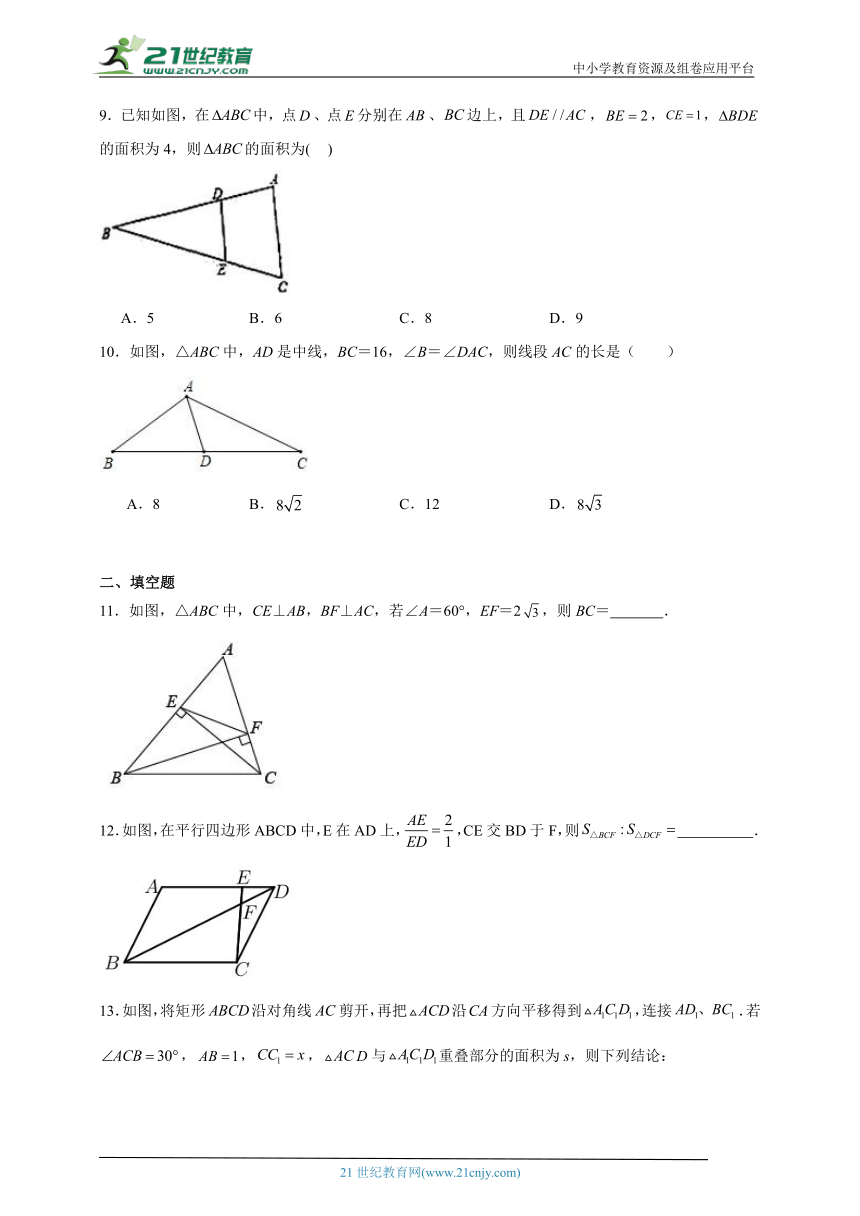
9.已知如图,在中,点、点分别在、边上,且,,,的面积为4,则的面积为( )
A.5 B.6 C.8 D.9
10.如图,△ABC中,AD是中线,BC=16,∠B=∠DAC,则线段AC的长是( )
A.8 B. C.12 D.
二、填空题
11.如图,△ABC中,CE⊥AB,BF⊥AC,若∠A=60°,EF=2,则BC= .
12.如图,在平行四边形ABCD中,E在AD上,,CE交BD于F,则 .
13.如图,将矩形沿对角线剪开,再把沿方向平移得到,连接.若,,,D与重叠部分的面积为s,则下列结论:
①;
②当时,四边形是菱形;
③当时,为等边三角形;
④;
其中正确的是 (填序号).
14.如图1,点D为直角三角形ABC的斜边AB上的中点,DE⊥AB交AC于E, 连EB、CD,线段CD与BF交于点F.若tanA=,则= .如图2,点D为直角三角形ABC的斜边AB上的一点,DE⊥AB交AC于E, 连EB、CD;线段CD与BF交于点F.若,tanA=,则= .
15.如图,在平面直角坐标系中,已如,,,在坐标轴上有一点,它与,两点形成的三角形与相似,则点的坐标是 .
16.如图,中,,点、分别在边、上,,,,那么的长为 .
17.如图,△OBC的边BC∥x轴,过点C的双曲线y=(k≠0)与△OBC的边OB交于点D,且OD:DB=1:2,若△OBC的面积等于8,则k的值为 .
18.某地为了更好地保护红军历史博物馆,经过精心的筹备规划,决定把原来博物馆的平面图扩大.如图,已知原来博物馆的平面图是,规划后博物馆的平面图是四边形,其中点A,B,C,D分别是边的中点.如果原来博物馆的平面图的面积为,则规划后博物馆的平面图占地面积为 .
19.已知△ABC∽△DEF,且它们的周长之比为1:3,则它们的相似比为 .
20.如图,在平面直角坐标系中,点在线段上,A点横坐标为,且有.若反比例函数和的图象分别经过A、B两点,则k的值为 .
三、解答题
21.如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC,
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求的值.
22.(1)如图①,将绕点旋转任意角度得到△,连接、,证明:.
(2)如图②,四边形和四边形均为正方形,连接,,求的值.
23.如图,△ABC中∠A=60°,∠B=40°,点D、E分别在△ABC的边AB、AC上,且∠ADE=80°.
(1)求证:△AED∽△ABC;
(2)若AD=4,AB=8,AE=5,求CE的长.
24.如图,矩形矩形,、分别为它们的短边,点在上,.
(1)求证:.
(2)若两个矩形的面积之和为,求矩形的面积.
25.如图1,B(2m,0),C(3m,0)是平面直角坐标系中两点,其中m为常数,且m>0,E(0,n)为y轴上一动点,以BC为边在x轴上方作矩形ABCD,使AB=2BC,画射线OA,把△ADC绕点C逆时针旋转90°得△A′D′C′,连接ED′,抛物线()过E,A′两点.
(1)填空:∠AOB= °,用m表示点A′的坐标:A′( , );
(2)当抛物线的顶点为A′,抛物线与线段AB交于点P,且时,△D′OE与△ABC是否相似?说明理由;
(3)若E与原点O重合,抛物线与射线OA的另一个交点为点M,过M作MN⊥y轴,垂足为N:
①求a,b,m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为10,请你探究a的取值范围.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
22.3相似三角形的性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知 ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:①DB=BE;②∠A=∠BHE;③AB=BH;④△BHD∽△BDG.其中正确的结论是( )
A.①②③④ B.①②③ C.①②④ D.②③④
2.已知△ABC中,AB=10,AC=8,D、E分别是AB、AC上的点,且AD=4,以A、D、E为顶点的三角形和△ABC相似,则AE的长是( )
A.5 B. C. D.5或
3.如图,已知 ABCD中,点M是BC的中点,且AM=6,BD=12,AD=4,则该平行四边形的面积为( )
A.24 B.36 C.48 D.72
4.如图,□ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
A.3:2 B.3:1 C.1:1 D.1:2
5.如图,中,点,分别在,上,,若,,则与的面积之比为( )
A. B. C. D.
6.如图,正方形中,点分别在上,是等边三角形,连接交于点,过点作于点,若,则下列结论:①;②;③;④⑤其中结论正确的个数有( )
A.2个 B.3个 C.4个 D.5个
7.由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.点,分别为,的中点,若PQ恰好经过点F,则的值为( )
A. B.3 C. D.4
8.如图,中,,,,则与的相似比是( )
A.3:2 B.2:3 C.3:5 D.5:3
9.已知如图,在中,点、点分别在、边上,且,,,的面积为4,则的面积为( )
A.5 B.6 C.8 D.9
10.如图,△ABC中,AD是中线,BC=16,∠B=∠DAC,则线段AC的长是( )
A.8 B. C.12 D.
二、填空题
11.如图,△ABC中,CE⊥AB,BF⊥AC,若∠A=60°,EF=2,则BC= .
12.如图,在平行四边形ABCD中,E在AD上,,CE交BD于F,则 .
13.如图,将矩形沿对角线剪开,再把沿方向平移得到,连接.若,,,D与重叠部分的面积为s,则下列结论:
①;
②当时,四边形是菱形;
③当时,为等边三角形;
④;
其中正确的是 (填序号).
14.如图1,点D为直角三角形ABC的斜边AB上的中点,DE⊥AB交AC于E, 连EB、CD,线段CD与BF交于点F.若tanA=,则= .如图2,点D为直角三角形ABC的斜边AB上的一点,DE⊥AB交AC于E, 连EB、CD;线段CD与BF交于点F.若,tanA=,则= .
15.如图,在平面直角坐标系中,已如,,,在坐标轴上有一点,它与,两点形成的三角形与相似,则点的坐标是 .
16.如图,中,,点、分别在边、上,,,,那么的长为 .
17.如图,△OBC的边BC∥x轴,过点C的双曲线y=(k≠0)与△OBC的边OB交于点D,且OD:DB=1:2,若△OBC的面积等于8,则k的值为 .
18.某地为了更好地保护红军历史博物馆,经过精心的筹备规划,决定把原来博物馆的平面图扩大.如图,已知原来博物馆的平面图是,规划后博物馆的平面图是四边形,其中点A,B,C,D分别是边的中点.如果原来博物馆的平面图的面积为,则规划后博物馆的平面图占地面积为 .
19.已知△ABC∽△DEF,且它们的周长之比为1:3,则它们的相似比为 .
20.如图,在平面直角坐标系中,点在线段上,A点横坐标为,且有.若反比例函数和的图象分别经过A、B两点,则k的值为 .
三、解答题
21.如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC,
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求的值.
22.(1)如图①,将绕点旋转任意角度得到△,连接、,证明:.
(2)如图②,四边形和四边形均为正方形,连接,,求的值.
23.如图,△ABC中∠A=60°,∠B=40°,点D、E分别在△ABC的边AB、AC上,且∠ADE=80°.
(1)求证:△AED∽△ABC;
(2)若AD=4,AB=8,AE=5,求CE的长.
24.如图,矩形矩形,、分别为它们的短边,点在上,.
(1)求证:.
(2)若两个矩形的面积之和为,求矩形的面积.
25.如图1,B(2m,0),C(3m,0)是平面直角坐标系中两点,其中m为常数,且m>0,E(0,n)为y轴上一动点,以BC为边在x轴上方作矩形ABCD,使AB=2BC,画射线OA,把△ADC绕点C逆时针旋转90°得△A′D′C′,连接ED′,抛物线()过E,A′两点.
(1)填空:∠AOB= °,用m表示点A′的坐标:A′( , );
(2)当抛物线的顶点为A′,抛物线与线段AB交于点P,且时,△D′OE与△ABC是否相似?说明理由;
(3)若E与原点O重合,抛物线与射线OA的另一个交点为点M,过M作MN⊥y轴,垂足为N:
①求a,b,m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为10,请你探究a的取值范围.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
