24.1 旋转分层练习(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
24.1旋转
学校:___________姓名:___________班级:___________考号:___________
一、单选题
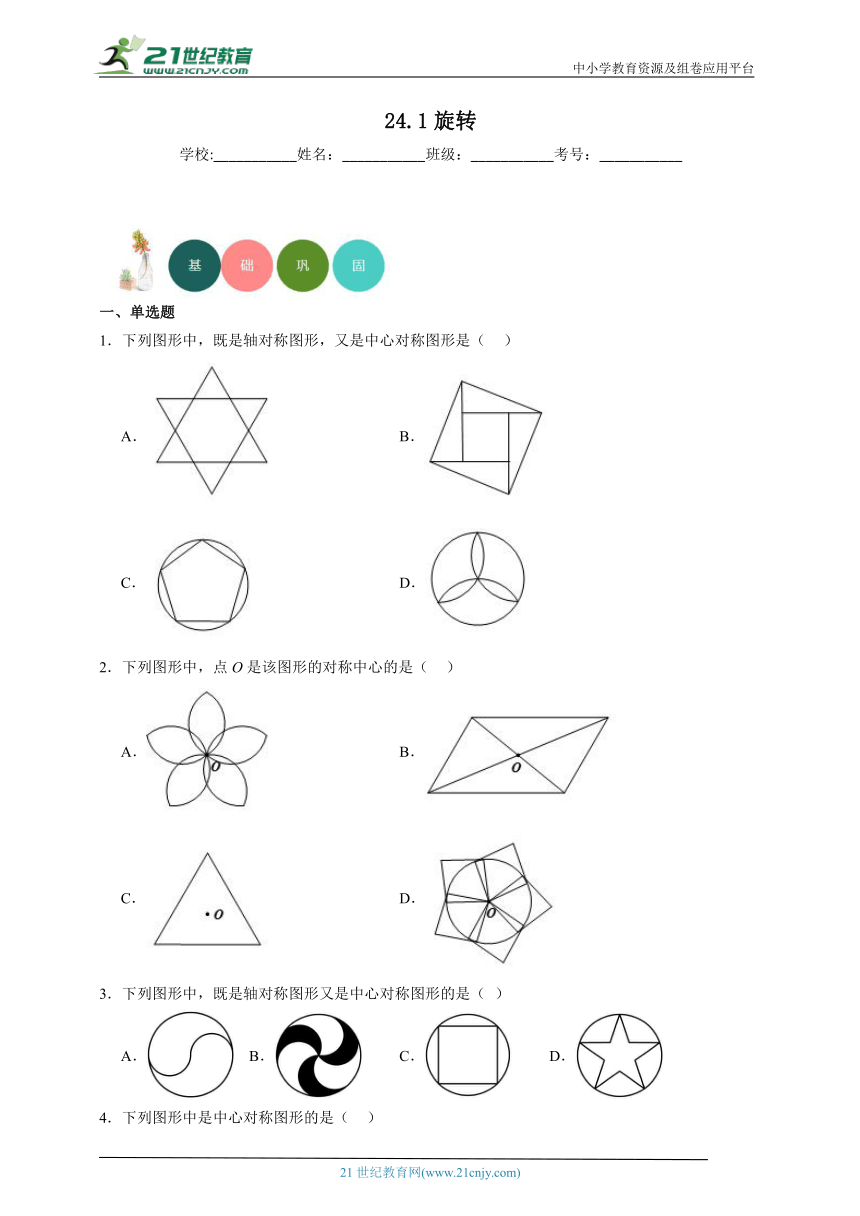
1.下列图形中,既是轴对称图形,又是中心对称图形是( )
A. B.
C. D.
2.下列图形中,点O是该图形的对称中心的是( )
A. B.
C. D.
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.下列图形中是中心对称图形的是( )
A. B. C. D.
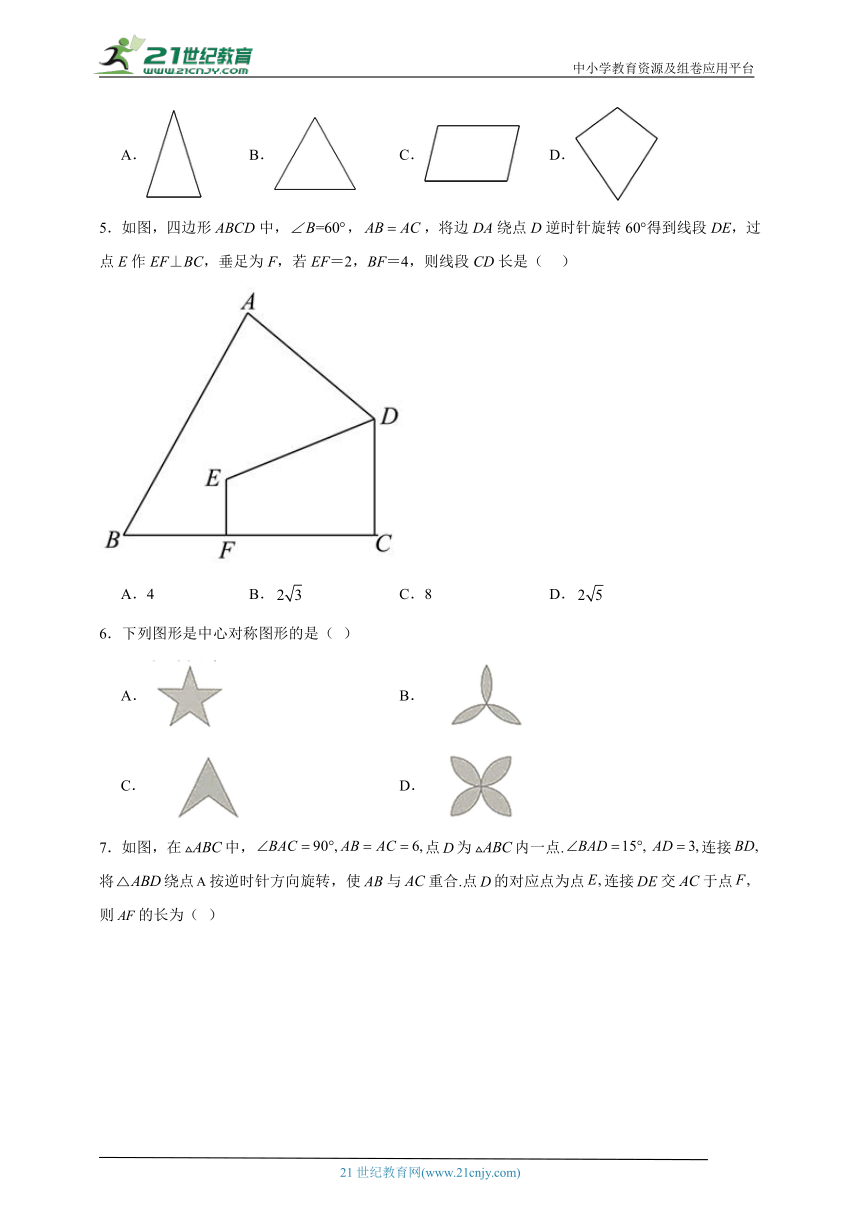
5.如图,四边形ABCD中,,,将边DA绕点D逆时针旋转60°得到线段DE,过点E作EF⊥BC,垂足为F,若EF=2,BF=4,则线段CD长是( )
A.4 B. C.8 D.
6.下列图形是中心对称图形的是( )
A. B.
C. D.
7.如图,在中,点为内一点.连接将绕点按逆时针方向旋转,使与重合.点的对应点为点连接交于点则的长为( )
A. B. C. D.
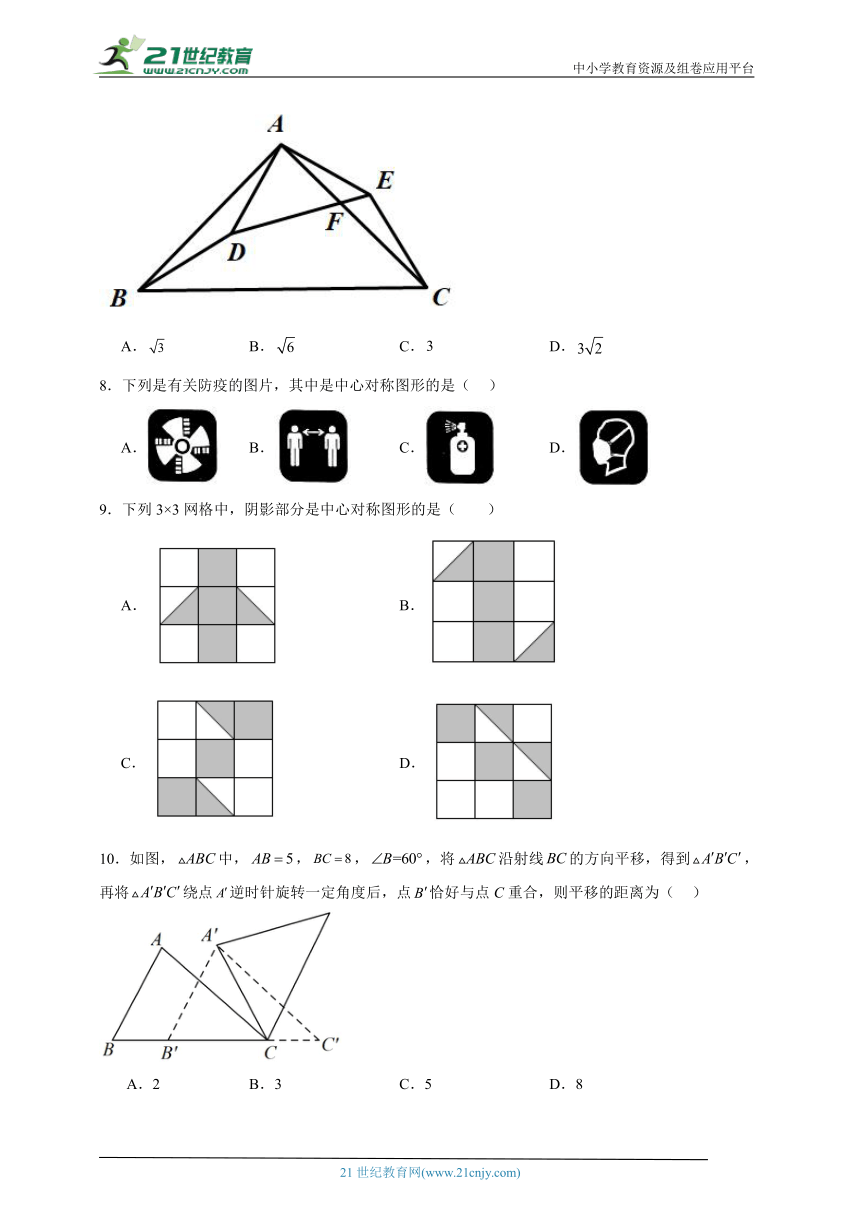
8.下列是有关防疫的图片,其中是中心对称图形的是( )
A. B. C. D.
9.下列3×3网格中,阴影部分是中心对称图形的是( )
A. B.
C. D.
10.如图,中,,,,将沿射线的方向平移,得到,再将绕点逆时针旋转一定角度后,点恰好与点C重合,则平移的距离为( )
A.2 B.3 C.5 D.8
二、填空题
11.如图,△AOB的边OB在x轴上,AC⊥x轴于C,D为AC上一点,将△CBD沿BD翻折,使点C落在AB边上的E点.已知∠AOB=60°,AO=4,点B的坐标为(8+2,0),则点D的坐标为 .
12.若将二次函数y=x2﹣4x+3的图象绕着点(﹣1,0)旋转180°,得到新的二次函数y=ax2+bx+c(a≠0),那么c的值为 .
13.如图,△ABC中,∠BAC=45°,∠ACB=30°,将△ABC绕点A顺时针旋转得到△A1B1C1,当C,B1,C1三点共线时,旋转角为α,连接BB1,交于AC于点D,下面结论:
①△AC1C为等腰三角形;②CA=CB1;③α=135°;④△AB1D∽△ACB1;⑤=中,正确的结论的序号为 .
14.如图,矩形放在平面直角坐标系中,,,将矩形绕原点按顺时针方向旋转得到矩形,则点的坐标是 .
15.如图中哪些图形绕其上的一点旋转180°,旋转前后的图形能完全重合?图 是.
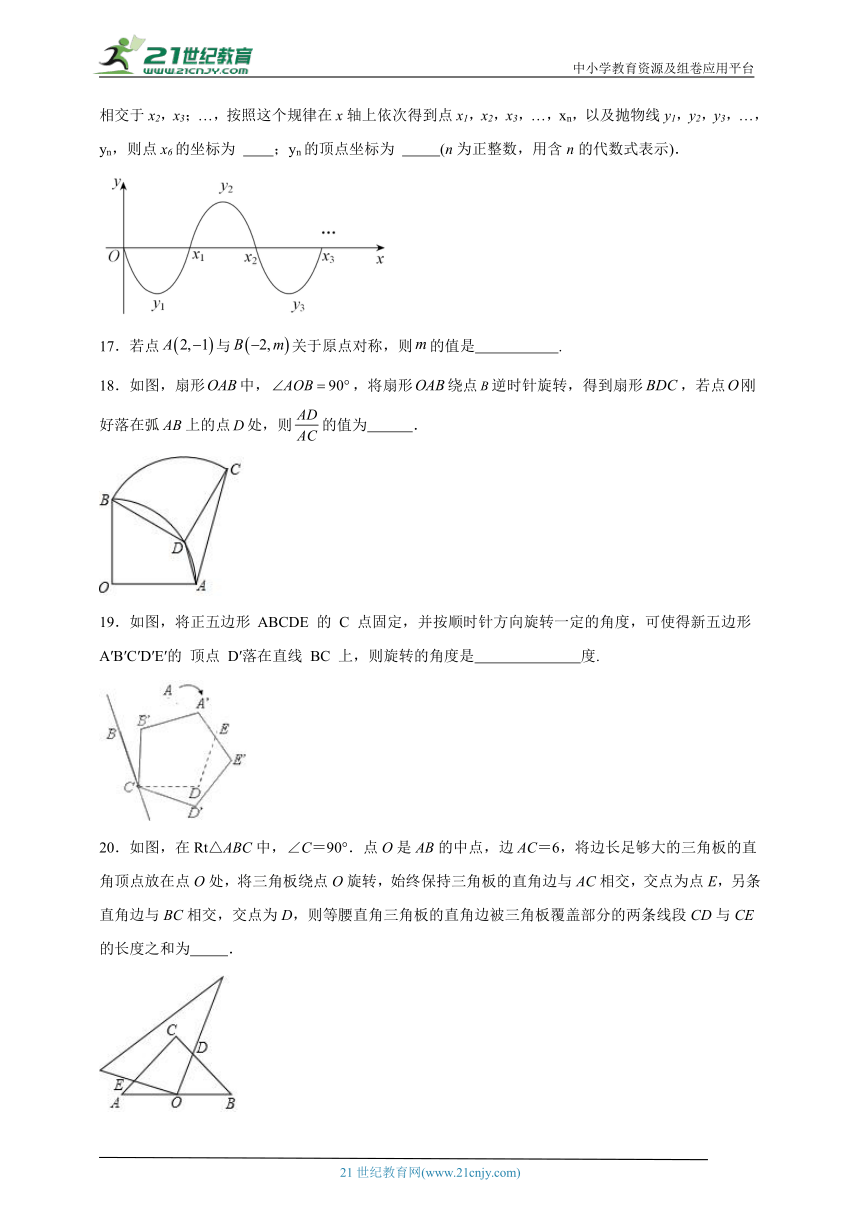
16.如图,在平面直角坐标系xOy中,抛物线y=x(x-5)(0≤x≤5)的图象记作y1,它与x轴的交于点O,x1,将y1绕x1旋转180°得到y2,y2与x轴相交于点x1,x2,将y2绕点x2旋转180°得到y3,y3与x轴相交于x2,x3;…,按照这个规律在x轴上依次得到点x1,x2,x3,…,xn,以及抛物线y1,y2,y3,…,yn,则点x6的坐标为 ;yn的顶点坐标为 (n为正整数,用含n的代数式表示).
17.若点与关于原点对称,则的值是 .
18.如图,扇形中,,将扇形绕点逆时针旋转,得到扇形,若点刚好落在弧上的点处,则的值为 .
19.如图,将正五边形 ABCDE 的 C 点固定,并按顺时针方向旋转一定的角度,可使得新五边形A′B′C′D′E′的 顶点 D′落在直线 BC 上,则旋转的角度是 度.
20.如图,在Rt△ABC中,∠C=90°.点O是AB的中点,边AC=6,将边长足够大的三角板的直角顶点放在点O处,将三角板绕点O旋转,始终保持三角板的直角边与AC相交,交点为点E,另条直角边与BC相交,交点为D,则等腰直角三角板的直角边被三角板覆盖部分的两条线段CD与CE的长度之和为 .
三、解答题
21.如图,四边形是矩形.
(1)尺规作图:将矩形绕着点逆时针旋转一定角度得到矩形,使点落在边上;
(2)若,,连接,求的长;
(3)若,求的度数(用含的表示).
22.在平面直角坐标系中,点的坐标为.
(1)如图1,若点在轴正半轴上,点,,,则点坐标为______
(2)如图2,若点在轴负半轴上,轴于点,轴于点,,交直线于点,若点,,求点坐标.
(3)如图3,若点,分别在,轴的正半轴上,,连接,点、是边上的两点,设,,则以线段、、长度为边长的三角形的形状为______(①钝角三角形;②直角三角形;③锐角三角形;④随线段的长度而定),请选择,并给出证明.
23.如图(1),在和中,,,,点E在内部,直线与交于点F,线段之间存在怎样的数量关系?
(1)先将问题特殊化.如图(2),当点D,F重合时,直接写出一个等式,表示之间的数量关系;
(2)再探究一般情形.如图(1),当点D,F不重合时,证明(1)中的结论仍然成立.
(3)如图(3),在和中,,,,点E在内部,直线与交于点F,直线与交于点G,点H为线段上一点,,与交于点I,若,,
则 (用含m,n的式子表示).
24.如图所示,的顶点坐标分别为,,,已知是由经过旋转变换得到的.
(1)分别写出旋转中心的坐标,旋转方向,旋转角度;
(2)①以(1)中的旋转中心为中心,分别画出和旋转后所得到的两个三角形(不需标上顶点字母);
②直接写出四个三角形及其内部所围成图形的面积.
25.在△ABC中,∠ACB=90°,∠BAC=60°,点D在斜边AB上,且满足BD=AB,将线段DB绕点D逆时针旋转至DE,记旋转角为α,连接AE,BE,以AE为斜边在其一侧作直角三角形AEF,且∠AFE=90°,∠EAF=60°,连接CF.
(1)如图1,当α=180°时,请直接写出线段BE与线段CF的数量关系;
(2)当0°<α<180°时,
①如图2,(1)中线段BE与线段CF的数量关系是否仍然成立?诸说明理由;
②如图3,当B,E,F三点共线时,连接CE,判断△CEF的形状,并证明.
参考答案:
1.A
2.B
3.C
4.C
5.D
6.D
7.B
8.A
9.C
10.B
11.
12.-15
13.①②④⑤
14.
15.②⑤/⑤②
16. (30,0)
17.1
18.
19.72°
20.6.
21.(1)略;
(2)
(3)
22.(1)
(2)N点坐标为;
(3)①略
23.(1);
(2)略;
(3).
24.(1),顺时针方向,
(2)①略;②20
25.(1)BE=2CF
(2)①成立;②等边三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.1旋转
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列图形中,既是轴对称图形,又是中心对称图形是( )
A. B.
C. D.
2.下列图形中,点O是该图形的对称中心的是( )
A. B.
C. D.
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.下列图形中是中心对称图形的是( )
A. B. C. D.
5.如图,四边形ABCD中,,,将边DA绕点D逆时针旋转60°得到线段DE,过点E作EF⊥BC,垂足为F,若EF=2,BF=4,则线段CD长是( )
A.4 B. C.8 D.
6.下列图形是中心对称图形的是( )
A. B.
C. D.
7.如图,在中,点为内一点.连接将绕点按逆时针方向旋转,使与重合.点的对应点为点连接交于点则的长为( )
A. B. C. D.
8.下列是有关防疫的图片,其中是中心对称图形的是( )
A. B. C. D.
9.下列3×3网格中,阴影部分是中心对称图形的是( )
A. B.
C. D.
10.如图,中,,,,将沿射线的方向平移,得到,再将绕点逆时针旋转一定角度后,点恰好与点C重合,则平移的距离为( )
A.2 B.3 C.5 D.8
二、填空题
11.如图,△AOB的边OB在x轴上,AC⊥x轴于C,D为AC上一点,将△CBD沿BD翻折,使点C落在AB边上的E点.已知∠AOB=60°,AO=4,点B的坐标为(8+2,0),则点D的坐标为 .
12.若将二次函数y=x2﹣4x+3的图象绕着点(﹣1,0)旋转180°,得到新的二次函数y=ax2+bx+c(a≠0),那么c的值为 .
13.如图,△ABC中,∠BAC=45°,∠ACB=30°,将△ABC绕点A顺时针旋转得到△A1B1C1,当C,B1,C1三点共线时,旋转角为α,连接BB1,交于AC于点D,下面结论:
①△AC1C为等腰三角形;②CA=CB1;③α=135°;④△AB1D∽△ACB1;⑤=中,正确的结论的序号为 .
14.如图,矩形放在平面直角坐标系中,,,将矩形绕原点按顺时针方向旋转得到矩形,则点的坐标是 .
15.如图中哪些图形绕其上的一点旋转180°,旋转前后的图形能完全重合?图 是.
16.如图,在平面直角坐标系xOy中,抛物线y=x(x-5)(0≤x≤5)的图象记作y1,它与x轴的交于点O,x1,将y1绕x1旋转180°得到y2,y2与x轴相交于点x1,x2,将y2绕点x2旋转180°得到y3,y3与x轴相交于x2,x3;…,按照这个规律在x轴上依次得到点x1,x2,x3,…,xn,以及抛物线y1,y2,y3,…,yn,则点x6的坐标为 ;yn的顶点坐标为 (n为正整数,用含n的代数式表示).
17.若点与关于原点对称,则的值是 .
18.如图,扇形中,,将扇形绕点逆时针旋转,得到扇形,若点刚好落在弧上的点处,则的值为 .
19.如图,将正五边形 ABCDE 的 C 点固定,并按顺时针方向旋转一定的角度,可使得新五边形A′B′C′D′E′的 顶点 D′落在直线 BC 上,则旋转的角度是 度.
20.如图,在Rt△ABC中,∠C=90°.点O是AB的中点,边AC=6,将边长足够大的三角板的直角顶点放在点O处,将三角板绕点O旋转,始终保持三角板的直角边与AC相交,交点为点E,另条直角边与BC相交,交点为D,则等腰直角三角板的直角边被三角板覆盖部分的两条线段CD与CE的长度之和为 .
三、解答题
21.如图,四边形是矩形.
(1)尺规作图:将矩形绕着点逆时针旋转一定角度得到矩形,使点落在边上;
(2)若,,连接,求的长;
(3)若,求的度数(用含的表示).
22.在平面直角坐标系中,点的坐标为.
(1)如图1,若点在轴正半轴上,点,,,则点坐标为______
(2)如图2,若点在轴负半轴上,轴于点,轴于点,,交直线于点,若点,,求点坐标.
(3)如图3,若点,分别在,轴的正半轴上,,连接,点、是边上的两点,设,,则以线段、、长度为边长的三角形的形状为______(①钝角三角形;②直角三角形;③锐角三角形;④随线段的长度而定),请选择,并给出证明.
23.如图(1),在和中,,,,点E在内部,直线与交于点F,线段之间存在怎样的数量关系?
(1)先将问题特殊化.如图(2),当点D,F重合时,直接写出一个等式,表示之间的数量关系;
(2)再探究一般情形.如图(1),当点D,F不重合时,证明(1)中的结论仍然成立.
(3)如图(3),在和中,,,,点E在内部,直线与交于点F,直线与交于点G,点H为线段上一点,,与交于点I,若,,
则 (用含m,n的式子表示).
24.如图所示,的顶点坐标分别为,,,已知是由经过旋转变换得到的.
(1)分别写出旋转中心的坐标,旋转方向,旋转角度;
(2)①以(1)中的旋转中心为中心,分别画出和旋转后所得到的两个三角形(不需标上顶点字母);
②直接写出四个三角形及其内部所围成图形的面积.
25.在△ABC中,∠ACB=90°,∠BAC=60°,点D在斜边AB上,且满足BD=AB,将线段DB绕点D逆时针旋转至DE,记旋转角为α,连接AE,BE,以AE为斜边在其一侧作直角三角形AEF,且∠AFE=90°,∠EAF=60°,连接CF.
(1)如图1,当α=180°时,请直接写出线段BE与线段CF的数量关系;
(2)当0°<α<180°时,
①如图2,(1)中线段BE与线段CF的数量关系是否仍然成立?诸说明理由;
②如图3,当B,E,F三点共线时,连接CE,判断△CEF的形状,并证明.
参考答案:
1.A
2.B
3.C
4.C
5.D
6.D
7.B
8.A
9.C
10.B
11.
12.-15
13.①②④⑤
14.
15.②⑤/⑤②
16. (30,0)
17.1
18.
19.72°
20.6.
21.(1)略;
(2)
(3)
22.(1)
(2)N点坐标为;
(3)①略
23.(1);
(2)略;
(3).
24.(1),顺时针方向,
(2)①略;②20
25.(1)BE=2CF
(2)①成立;②等边三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
