24.2 圆的基本性质分层练习(含答案)
文档属性
| 名称 | 24.2 圆的基本性质分层练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 681.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
24.2圆的基本性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在平面直角坐标系中,的半径为5,点P的坐标为,则点P与的位置关系是( )
A.点P在内 B.点P在上 C.点P在外 D.无法确定.
2.下列说法不正确的是( )
A.任何一个三角形都有外接圆 B.等边三角形的外心是这个三角形的中心
C.直角三角形的外心是其斜边的中点 D.一个三角形的外心不可能在三角形的外部
3.下列命题:半圆是中心对称图形;相等的圆心角所对的弧相等;平分弦的直径垂直于弦;圆内两条非直径的相交弦不能互相平分,其中正确的有( )
A.个 B.个 C.个 D.个
4.如图,是圆的直径,于,,,则为( )
A.2 B.3 C.4 D.3.5
5.已知AB是的弦,半径于点D,若,,则的半径为( )
A. B. C. D.
6.如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( )
A.等于24 B.最小为24 C.等于48 D.最大为48
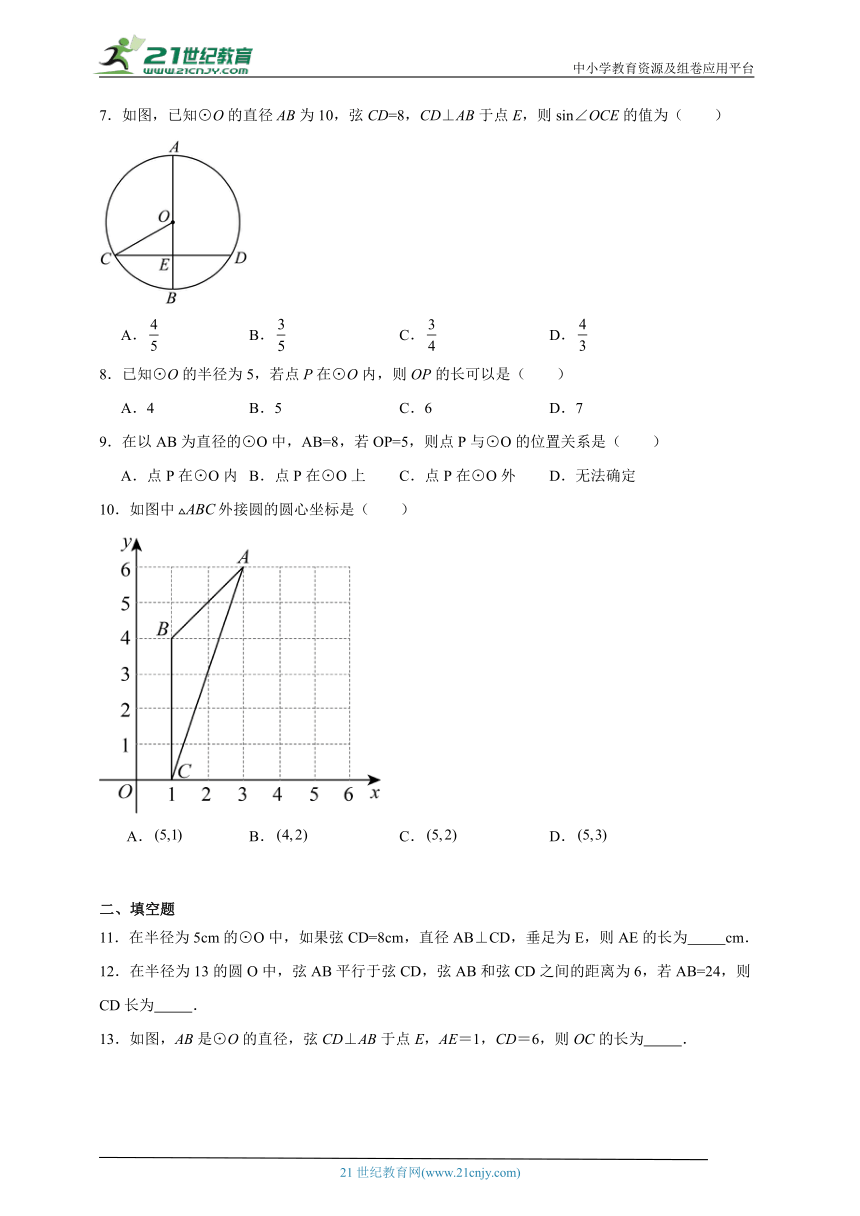
7.如图,已知⊙O的直径AB为10,弦CD=8,CD⊥AB于点E,则sin∠OCE的值为( )
A. B. C. D.
8.已知⊙O的半径为5,若点P在⊙O内,则OP的长可以是( )
A.4 B.5 C.6 D.7
9.在以AB为直径的⊙O中,AB=8,若OP=5,则点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法确定
10.如图中外接圆的圆心坐标是( )
A. B. C. D.
二、填空题
11.在半径为5cm的⊙O中,如果弦CD=8cm,直径AB⊥CD,垂足为E,则AE的长为 cm.
12.在半径为13的圆O中,弦AB平行于弦CD,弦AB和弦CD之间的距离为6,若AB=24,则CD长为 .
13.如图,AB是⊙O的直径,弦CD⊥AB于点E,AE=1,CD=6,则OC的长为 .
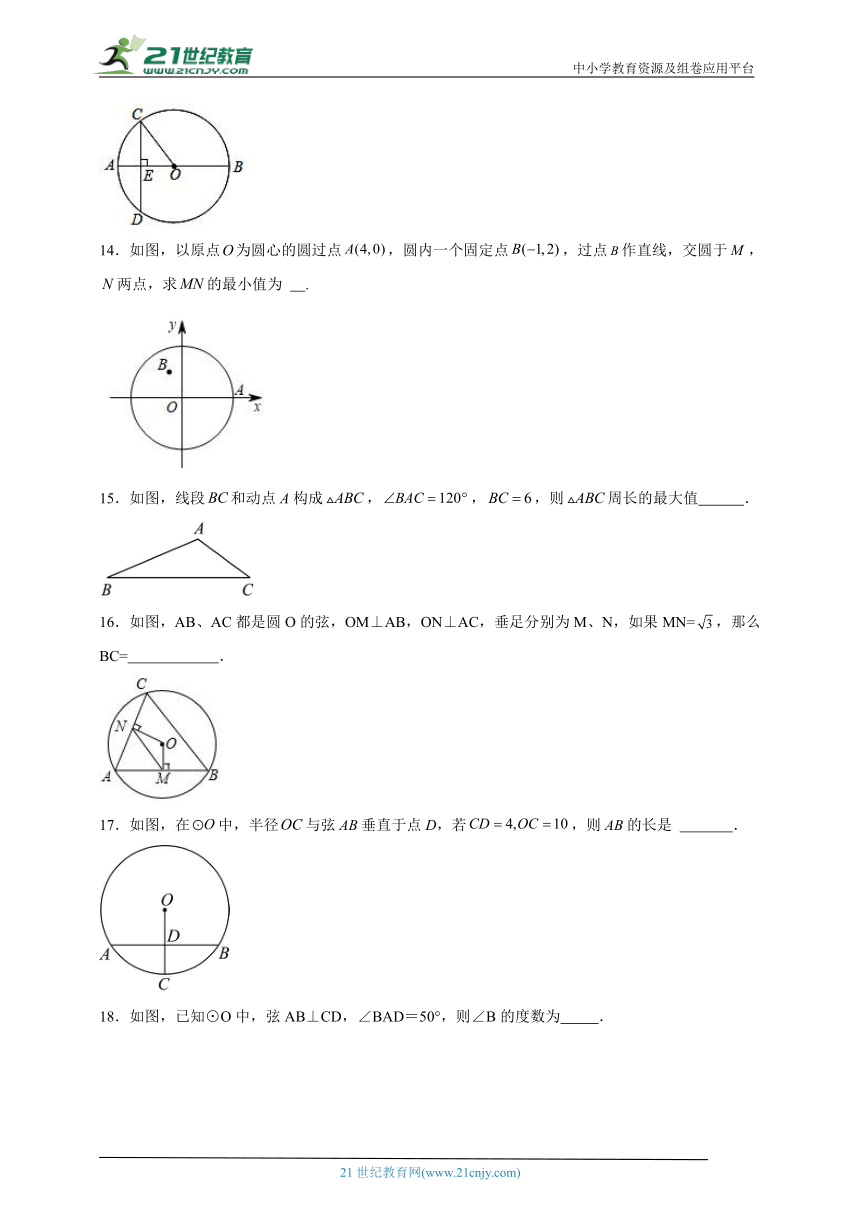
14.如图,以原点为圆心的圆过点,圆内一个固定点,过点作直线,交圆于,两点,求的最小值为 .
15.如图,线段和动点A构成,,,则周长的最大值 .
16.如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果MN=,那么BC= .
17.如图,在中,半径与弦垂直于点D,若,则的长是 .
18.如图,已知⊙O中,弦AB⊥CD,∠BAD=50°,则∠B的度数为 .
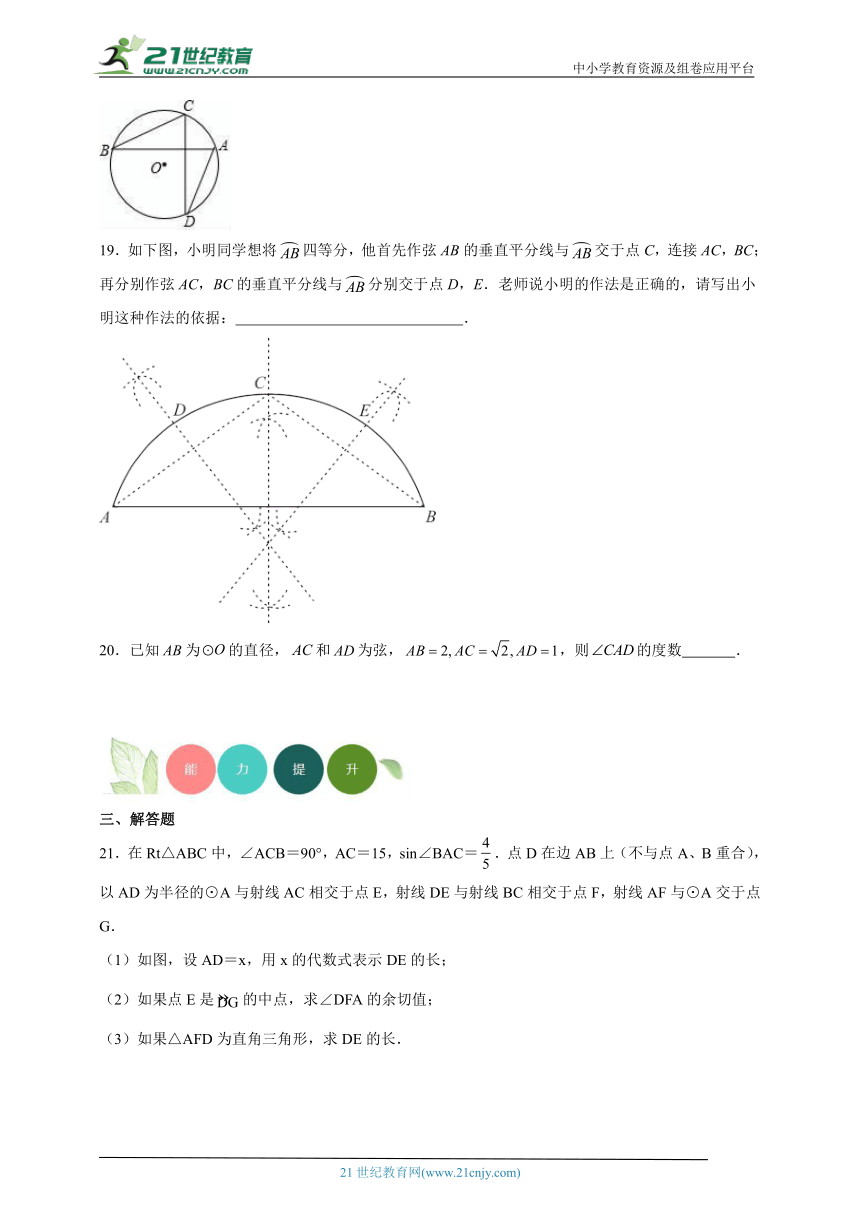
19.如下图,小明同学想将四等分,他首先作弦AB的垂直平分线与交于点C,连接AC,BC;再分别作弦AC,BC的垂直平分线与分别交于点D,E.老师说小明的作法是正确的,请写出小明这种作法的依据: .
20.已知为的直径,和为弦,,则的度数 .
三、解答题
21.在Rt△ABC中,∠ACB=90°,AC=15,sin∠BAC=.点D在边AB上(不与点A、B重合),以AD为半径的⊙A与射线AC相交于点E,射线DE与射线BC相交于点F,射线AF与⊙A交于点G.
(1)如图,设AD=x,用x的代数式表示DE的长;
(2)如果点E是的中点,求∠DFA的余切值;
(3)如果△AFD为直角三角形,求DE的长.
22.如图,弓形铁片所在圆的圆心为点O,半径为13cm,弓形的高(弧的中点到弦的距离)的长度为8cm,求弦的长度.
23.如图,为的直径,C是延长线上一点,点D在上,且,的延长线交于点E,若,试求的度数.
24.实践与探究:
操作一:已知边长为8正方形纸片ABCD,将正方形纸片ABCD对折,使得点A和点D重合,点B和点C重合,折痕为EF.
操作二:如图①,将正方形纸片ABCD沿过点B的直线翻折,点A的对应点为点N,折痕为BM.当N落在EF上时,BF和BN的数量关系是______;的大小为______.
操作三:如图②,再将纸片沿直线BN翻折,点M的对应点为点.当点在CD上时,求的度数.
操作四:如图③,当点M沿运动时,EN中点为K,连接DK,DK的最小值为______.
参考答案:
1.B
2.D
3.C
4.B
5.B
6.A
7.B
8.A
9.C
10.C
11.2cm或8cm.
12.8或4.
13.5
14.
15./
16.2
17.16
18.40°
19.①圆是轴对称图形,任何一条直径所在直线都是它的对称轴;
②垂直于弦的直径平分弦,并且平分弦所对的两条弧
20.105°或15°
21.(1);(2)∠DFA的余切值为;(3)DE的长为或.
22.
23..
24.操作二:,;操作三:;操作四:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.2圆的基本性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在平面直角坐标系中,的半径为5,点P的坐标为,则点P与的位置关系是( )
A.点P在内 B.点P在上 C.点P在外 D.无法确定.
2.下列说法不正确的是( )
A.任何一个三角形都有外接圆 B.等边三角形的外心是这个三角形的中心
C.直角三角形的外心是其斜边的中点 D.一个三角形的外心不可能在三角形的外部
3.下列命题:半圆是中心对称图形;相等的圆心角所对的弧相等;平分弦的直径垂直于弦;圆内两条非直径的相交弦不能互相平分,其中正确的有( )
A.个 B.个 C.个 D.个
4.如图,是圆的直径,于,,,则为( )
A.2 B.3 C.4 D.3.5
5.已知AB是的弦,半径于点D,若,,则的半径为( )
A. B. C. D.
6.如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( )
A.等于24 B.最小为24 C.等于48 D.最大为48
7.如图,已知⊙O的直径AB为10,弦CD=8,CD⊥AB于点E,则sin∠OCE的值为( )
A. B. C. D.
8.已知⊙O的半径为5,若点P在⊙O内,则OP的长可以是( )
A.4 B.5 C.6 D.7
9.在以AB为直径的⊙O中,AB=8,若OP=5,则点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法确定
10.如图中外接圆的圆心坐标是( )
A. B. C. D.
二、填空题
11.在半径为5cm的⊙O中,如果弦CD=8cm,直径AB⊥CD,垂足为E,则AE的长为 cm.
12.在半径为13的圆O中,弦AB平行于弦CD,弦AB和弦CD之间的距离为6,若AB=24,则CD长为 .
13.如图,AB是⊙O的直径,弦CD⊥AB于点E,AE=1,CD=6,则OC的长为 .
14.如图,以原点为圆心的圆过点,圆内一个固定点,过点作直线,交圆于,两点,求的最小值为 .
15.如图,线段和动点A构成,,,则周长的最大值 .
16.如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果MN=,那么BC= .
17.如图,在中,半径与弦垂直于点D,若,则的长是 .
18.如图,已知⊙O中,弦AB⊥CD,∠BAD=50°,则∠B的度数为 .
19.如下图,小明同学想将四等分,他首先作弦AB的垂直平分线与交于点C,连接AC,BC;再分别作弦AC,BC的垂直平分线与分别交于点D,E.老师说小明的作法是正确的,请写出小明这种作法的依据: .
20.已知为的直径,和为弦,,则的度数 .
三、解答题
21.在Rt△ABC中,∠ACB=90°,AC=15,sin∠BAC=.点D在边AB上(不与点A、B重合),以AD为半径的⊙A与射线AC相交于点E,射线DE与射线BC相交于点F,射线AF与⊙A交于点G.
(1)如图,设AD=x,用x的代数式表示DE的长;
(2)如果点E是的中点,求∠DFA的余切值;
(3)如果△AFD为直角三角形,求DE的长.
22.如图,弓形铁片所在圆的圆心为点O,半径为13cm,弓形的高(弧的中点到弦的距离)的长度为8cm,求弦的长度.
23.如图,为的直径,C是延长线上一点,点D在上,且,的延长线交于点E,若,试求的度数.
24.实践与探究:
操作一:已知边长为8正方形纸片ABCD,将正方形纸片ABCD对折,使得点A和点D重合,点B和点C重合,折痕为EF.
操作二:如图①,将正方形纸片ABCD沿过点B的直线翻折,点A的对应点为点N,折痕为BM.当N落在EF上时,BF和BN的数量关系是______;的大小为______.
操作三:如图②,再将纸片沿直线BN翻折,点M的对应点为点.当点在CD上时,求的度数.
操作四:如图③,当点M沿运动时,EN中点为K,连接DK,DK的最小值为______.
参考答案:
1.B
2.D
3.C
4.B
5.B
6.A
7.B
8.A
9.C
10.C
11.2cm或8cm.
12.8或4.
13.5
14.
15./
16.2
17.16
18.40°
19.①圆是轴对称图形,任何一条直径所在直线都是它的对称轴;
②垂直于弦的直径平分弦,并且平分弦所对的两条弧
20.105°或15°
21.(1);(2)∠DFA的余切值为;(3)DE的长为或.
22.
23..
24.操作二:,;操作三:;操作四:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
