24.5 三角形的内切圆分层练习(含答案)
文档属性
| 名称 | 24.5 三角形的内切圆分层练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 627.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 08:23:51 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
24.5三角形的内切圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD,BE,CE,若∠CBD=32°,则∠BEC的度数为( )
A.128° B.126° C.122° D.120°
2.下列叙述:①圆内接四边形对角互补;②矩形一定有一个外接圆;③三角形的外心到三角形三边的距离相等;④三角形一定有内切圆,其中真命题的个数有( )
A.4个 B.3个 C.2个 D.1个
3.已知的内切圆的半径为,且,的周长为16,则的长为( )
A.3 B.4 C.5 D.6
4.下列说法中,正确的是( )
A.相等的圆心角所对的弧相等 B.相等的弧所对的圆周角相等
C.三点确定一个圆 D.三角形的内心到三角形各顶点的距离都相等
5.如图所示,在中,,截的三边所得的弦长相等,则( )
A. B. C. D.
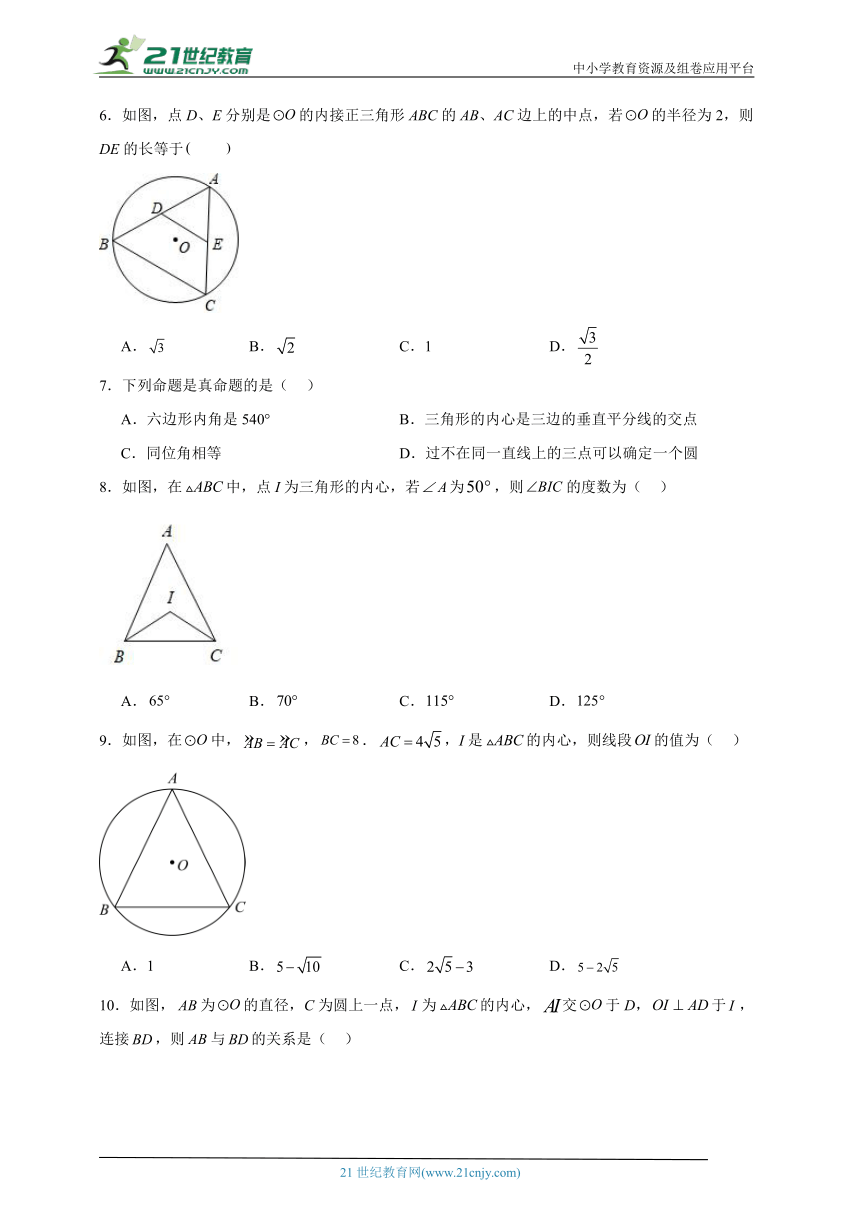
6.如图,点D、E分别是的内接正三角形ABC的AB、AC边上的中点,若的半径为2,则DE的长等于
A. B. C.1 D.
7.下列命题是真命题的是( )
A.六边形内角是540° B.三角形的内心是三边的垂直平分线的交点
C.同位角相等 D.过不在同一直线上的三点可以确定一个圆
8.如图,在中,点I为三角形的内心,若为,则的度数为( )
A. B. C. D.
9.如图,在中,,.,I是的内心,则线段的值为( )
A.1 B. C. D.
10.如图,为的直径,C为圆上一点,为的内心,交于D,于,连接,则与的关系是( )
A. B. C. D.
二、填空题
11.如图,内切于,切点分别为、、,若,,,则图中阴影部分的面积是 .
12.若一三角形的三边长分别为10、24、26,则此三角形的内切圆半径为 .
13.如图,中,是斜边上的高,,三个直角三角形、、的内切圆半径分别为,则的值是 .
14.在RtABC中,∠C=90°,AB=5,BC=4,求内切圆半径 .
15.边长为的正三角形的内切圆半径是 .
16.在中,,则的内切圆的周长为 .
17.如图,点是的内心,若,则 .
18.已知三角形的三边分别为3cm、4cm、5cm,则这个三角形内切圆的半径是 .
19.如图,圆内接,,点I是内心,则的度数为 .
20.如图,为半圆的直径,是半圆弧上任一点,正方形的一边在直线上,另一边过的内切圆圆心,且点在半圆弧上,已知,则的面积为 .
三、解答题
21.如图,⊙I切△ABC的边分别为D,E,F,∠B=70°,∠C=60°,M是 上的动点(与D,E不重合),∠DMF的大小一定吗?若一定,求出∠DMF的大小;若不一定,请说明理由.
22.在平面直角坐标系中,O为原点,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,现将正方形OABC绕点O顺时针旋转.
(1)如图①,当点A的对应的A′落在直线y=x上时,点A′的对应坐标为________;点B的对应点B′的坐标为_________;
(2)旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N,当A点第一次落在直线y=x上时,停止旋转.
①如图2,在正方形OABC旋转过程中,线段AM,MN,NC三者满足什么样的数量关系?请说明理由;
②当AC∥MN时,求△MBN内切圆的半径(直接写出结果即可)
23.图,在中,AB=AC,⊙O是的外接圆,点D在⊙O上且∠BCD=∠ACB,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF.
(1)求证:AF是⊙O的切线;
(2)若点G是的内心,,求BG的长.
参考答案:
1.C
2.B
3.C
4.B
5.B
6.A
7.D
8.C
9.D
10.C
11./
12.4.
13./2.4
14.1
15.
16.
17.
18.1.
19./116度
20.64
21.∠DMF的大小一定,∠DMF=65°.
22.(1),;(2)①AM+CN=MN,②.
23.(1)略
(2)5
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.5三角形的内切圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD,BE,CE,若∠CBD=32°,则∠BEC的度数为( )
A.128° B.126° C.122° D.120°
2.下列叙述:①圆内接四边形对角互补;②矩形一定有一个外接圆;③三角形的外心到三角形三边的距离相等;④三角形一定有内切圆,其中真命题的个数有( )
A.4个 B.3个 C.2个 D.1个
3.已知的内切圆的半径为,且,的周长为16,则的长为( )
A.3 B.4 C.5 D.6
4.下列说法中,正确的是( )
A.相等的圆心角所对的弧相等 B.相等的弧所对的圆周角相等
C.三点确定一个圆 D.三角形的内心到三角形各顶点的距离都相等
5.如图所示,在中,,截的三边所得的弦长相等,则( )
A. B. C. D.
6.如图,点D、E分别是的内接正三角形ABC的AB、AC边上的中点,若的半径为2,则DE的长等于
A. B. C.1 D.
7.下列命题是真命题的是( )
A.六边形内角是540° B.三角形的内心是三边的垂直平分线的交点
C.同位角相等 D.过不在同一直线上的三点可以确定一个圆
8.如图,在中,点I为三角形的内心,若为,则的度数为( )
A. B. C. D.
9.如图,在中,,.,I是的内心,则线段的值为( )
A.1 B. C. D.
10.如图,为的直径,C为圆上一点,为的内心,交于D,于,连接,则与的关系是( )
A. B. C. D.
二、填空题
11.如图,内切于,切点分别为、、,若,,,则图中阴影部分的面积是 .
12.若一三角形的三边长分别为10、24、26,则此三角形的内切圆半径为 .
13.如图,中,是斜边上的高,,三个直角三角形、、的内切圆半径分别为,则的值是 .
14.在RtABC中,∠C=90°,AB=5,BC=4,求内切圆半径 .
15.边长为的正三角形的内切圆半径是 .
16.在中,,则的内切圆的周长为 .
17.如图,点是的内心,若,则 .
18.已知三角形的三边分别为3cm、4cm、5cm,则这个三角形内切圆的半径是 .
19.如图,圆内接,,点I是内心,则的度数为 .
20.如图,为半圆的直径,是半圆弧上任一点,正方形的一边在直线上,另一边过的内切圆圆心,且点在半圆弧上,已知,则的面积为 .
三、解答题
21.如图,⊙I切△ABC的边分别为D,E,F,∠B=70°,∠C=60°,M是 上的动点(与D,E不重合),∠DMF的大小一定吗?若一定,求出∠DMF的大小;若不一定,请说明理由.
22.在平面直角坐标系中,O为原点,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,现将正方形OABC绕点O顺时针旋转.
(1)如图①,当点A的对应的A′落在直线y=x上时,点A′的对应坐标为________;点B的对应点B′的坐标为_________;
(2)旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N,当A点第一次落在直线y=x上时,停止旋转.
①如图2,在正方形OABC旋转过程中,线段AM,MN,NC三者满足什么样的数量关系?请说明理由;
②当AC∥MN时,求△MBN内切圆的半径(直接写出结果即可)
23.图,在中,AB=AC,⊙O是的外接圆,点D在⊙O上且∠BCD=∠ACB,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF.
(1)求证:AF是⊙O的切线;
(2)若点G是的内心,,求BG的长.
参考答案:
1.C
2.B
3.C
4.B
5.B
6.A
7.D
8.C
9.D
10.C
11./
12.4.
13./2.4
14.1
15.
16.
17.
18.1.
19./116度
20.64
21.∠DMF的大小一定,∠DMF=65°.
22.(1),;(2)①AM+CN=MN,②.
23.(1)略
(2)5
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
