24.6 正多边形与圆分层练习(含答案)
文档属性
| 名称 | 24.6 正多边形与圆分层练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 650.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
24.6正多边形与圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.圆内接正六边形的边长为 3,则该圆的直径长为( )
A.3 B.3 C.3 D.6
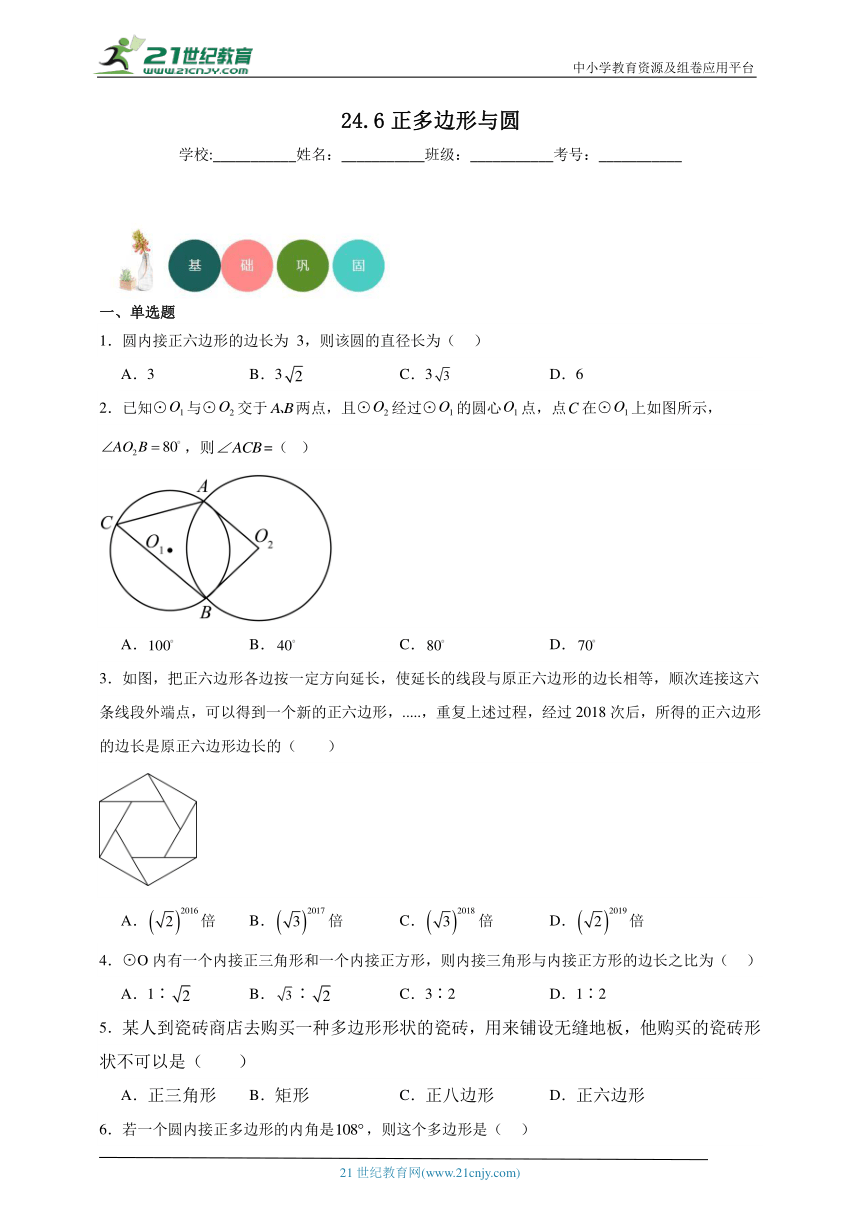
2.已知⊙与⊙交于两点,且⊙经过⊙的圆心点,点在⊙上如图所示,,则=( )
A. B. C. D.
3.如图,把正六边形各边按一定方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点,可以得到一个新的正六边形,.....,重复上述过程,经过2018次后,所得的正六边形的边长是原正六边形边长的( )
A.倍 B.倍 C.倍 D.倍
4.⊙O内有一个内接正三角形和一个内接正方形,则内接三角形与内接正方形的边长之比为( )
A.1∶ B.∶ C.3∶2 D.1∶2
5.某人到瓷砖商店去购买一种多边形形状的瓷砖,用来铺设无缝地板,他购买的瓷砖形状不可以是( )
A.正三角形 B.矩形 C.正八边形 D.正六边形
6.若一个圆内接正多边形的内角是,则这个多边形是( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
7.下列关于正多边形的叙述,正确的是( )
A.正七边形既是轴对称图形又是中心对称图形
B.存在一个正多边形,它的外角和为
C.任何正多边形都有一个外接圆
D.不存在每个外角都是对应每个内角两倍的正多边形
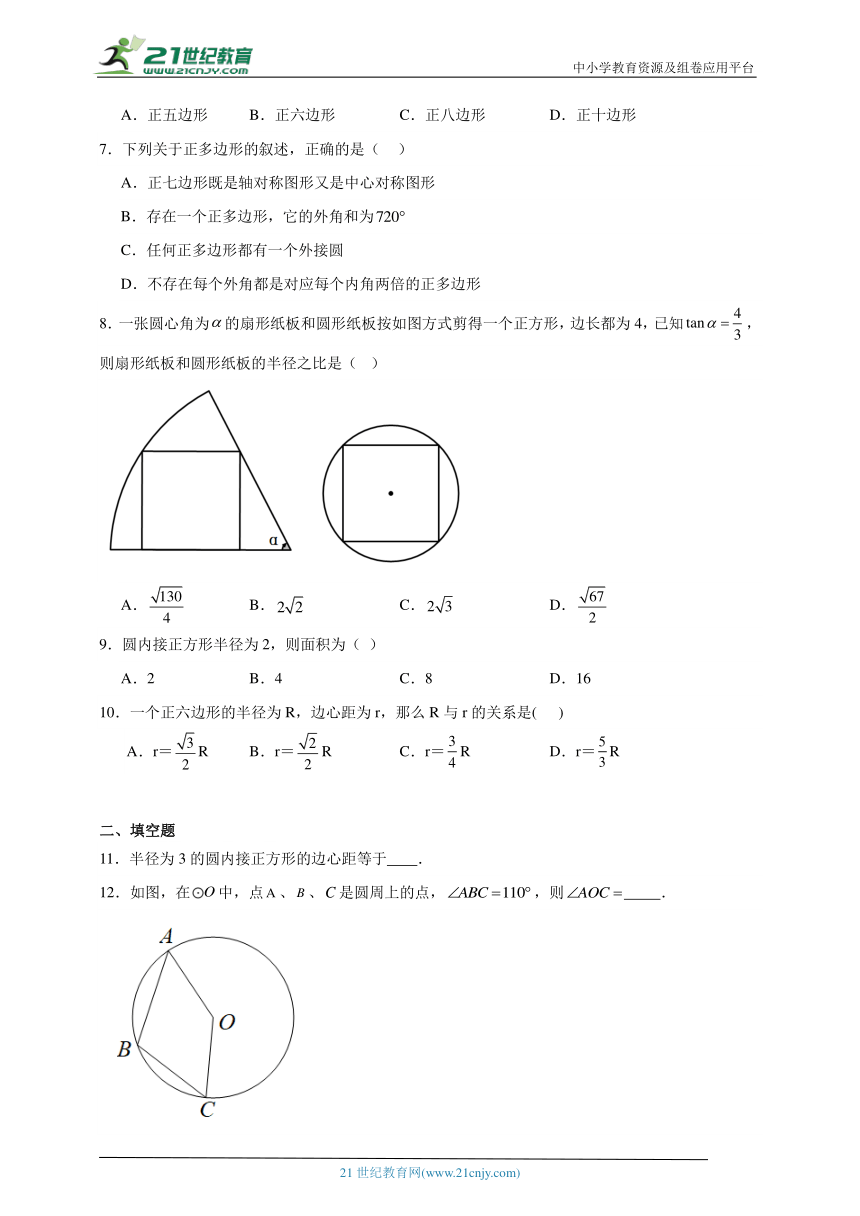
8.一张圆心角为的扇形纸板和圆形纸板按如图方式剪得一个正方形,边长都为4,已知,则扇形纸板和圆形纸板的半径之比是( )
A. B. C. D.
9.圆内接正方形半径为2,则面积为( )
A.2 B.4 C.8 D.16
10.一个正六边形的半径为R,边心距为r,那么R与r的关系是( )
A.r=R B.r=R C.r=R D.r=R
二、填空题
11.半径为3的圆内接正方形的边心距等于 .
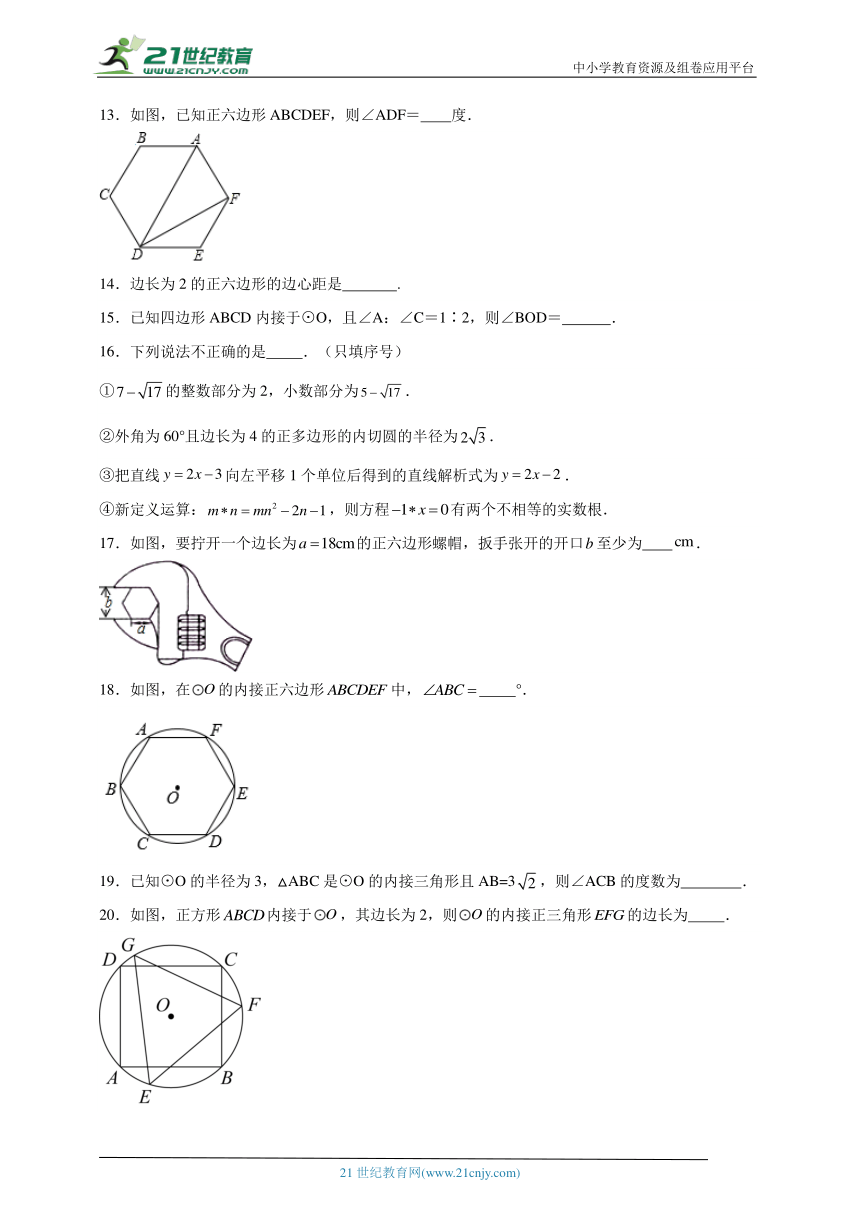
12.如图,在中,点、、是圆周上的点,,则 .
13.如图,已知正六边形ABCDEF,则∠ADF= 度.
14.边长为2的正六边形的边心距是 .
15.已知四边形ABCD内接于⊙O,且∠A:∠C=1∶2,则∠BOD= .
16.下列说法不正确的是 .(只填序号)
①的整数部分为2,小数部分为.
②外角为60°且边长为4的正多边形的内切圆的半径为.
③把直线向左平移1个单位后得到的直线解析式为.
④新定义运算:,则方程有两个不相等的实数根.
17.如图,要拧开一个边长为的正六边形螺帽,扳手张开的开口至少为 .
18.如图,在的内接正六边形中, °.
19.已知⊙O的半径为3,△ABC是⊙O的内接三角形且AB=3,则∠ACB的度数为 .
20.如图,正方形内接于,其边长为2,则的内接正三角形的边长为 .
三、解答题
21.如图,在中的内接四边形中,,为弧上一点.
(1)若,求和的度数;
(2)若,求证:为等边三角形.
22.如图,在边长为1个单位长度的小正方形组成的网格中,按要求完成下面的问题:
(1)以图中的O为位似中心,将△ABC作位似变换且缩小到原来的一半,得到△A'B'C',再把△A'B'C'绕点B'逆时针旋转90°得到△A″B'C″;
(2)求点A→A'→A″所经过的路线长.
23.已知:内接于,,P是外一点.
(Ⅰ)如图①,点P在上,若,求和的大小;
(Ⅱ)如图②,点P在外,是的直径,与相切于点B,若,求的大小.
24.如图,有一个圆O和两个正六边形T1,T2. T1的6个顶点都在圆周上,T2的6条边都和圆O相切(我们称T1,T2分别为圆O的内接正六边形和外切正六边形).
(1)设T1,T2的边长分别为a,b,圆O的半径为r,求r:a及r:b的值;
(2)求正六边形T1,T2的面积比S1:S2的值.
参考答案:
1.D
2.D
3.C
4.B
5.C
6.A
7.C
8.A
9.C
10.A
11.
12.
13.30
14.
15.120°
16.①②④
17.
18.
19.45°或135°
20.
21.(1)=70°,=125°;(2)略.
22.(1)略;(2)2+
23.(Ⅰ),;(Ⅱ).
24.(1)1:1,:2(2)3:4
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.6正多边形与圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.圆内接正六边形的边长为 3,则该圆的直径长为( )
A.3 B.3 C.3 D.6
2.已知⊙与⊙交于两点,且⊙经过⊙的圆心点,点在⊙上如图所示,,则=( )
A. B. C. D.
3.如图,把正六边形各边按一定方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点,可以得到一个新的正六边形,.....,重复上述过程,经过2018次后,所得的正六边形的边长是原正六边形边长的( )
A.倍 B.倍 C.倍 D.倍
4.⊙O内有一个内接正三角形和一个内接正方形,则内接三角形与内接正方形的边长之比为( )
A.1∶ B.∶ C.3∶2 D.1∶2
5.某人到瓷砖商店去购买一种多边形形状的瓷砖,用来铺设无缝地板,他购买的瓷砖形状不可以是( )
A.正三角形 B.矩形 C.正八边形 D.正六边形
6.若一个圆内接正多边形的内角是,则这个多边形是( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
7.下列关于正多边形的叙述,正确的是( )
A.正七边形既是轴对称图形又是中心对称图形
B.存在一个正多边形,它的外角和为
C.任何正多边形都有一个外接圆
D.不存在每个外角都是对应每个内角两倍的正多边形
8.一张圆心角为的扇形纸板和圆形纸板按如图方式剪得一个正方形,边长都为4,已知,则扇形纸板和圆形纸板的半径之比是( )
A. B. C. D.
9.圆内接正方形半径为2,则面积为( )
A.2 B.4 C.8 D.16
10.一个正六边形的半径为R,边心距为r,那么R与r的关系是( )
A.r=R B.r=R C.r=R D.r=R
二、填空题
11.半径为3的圆内接正方形的边心距等于 .
12.如图,在中,点、、是圆周上的点,,则 .
13.如图,已知正六边形ABCDEF,则∠ADF= 度.
14.边长为2的正六边形的边心距是 .
15.已知四边形ABCD内接于⊙O,且∠A:∠C=1∶2,则∠BOD= .
16.下列说法不正确的是 .(只填序号)
①的整数部分为2,小数部分为.
②外角为60°且边长为4的正多边形的内切圆的半径为.
③把直线向左平移1个单位后得到的直线解析式为.
④新定义运算:,则方程有两个不相等的实数根.
17.如图,要拧开一个边长为的正六边形螺帽,扳手张开的开口至少为 .
18.如图,在的内接正六边形中, °.
19.已知⊙O的半径为3,△ABC是⊙O的内接三角形且AB=3,则∠ACB的度数为 .
20.如图,正方形内接于,其边长为2,则的内接正三角形的边长为 .
三、解答题
21.如图,在中的内接四边形中,,为弧上一点.
(1)若,求和的度数;
(2)若,求证:为等边三角形.
22.如图,在边长为1个单位长度的小正方形组成的网格中,按要求完成下面的问题:
(1)以图中的O为位似中心,将△ABC作位似变换且缩小到原来的一半,得到△A'B'C',再把△A'B'C'绕点B'逆时针旋转90°得到△A″B'C″;
(2)求点A→A'→A″所经过的路线长.
23.已知:内接于,,P是外一点.
(Ⅰ)如图①,点P在上,若,求和的大小;
(Ⅱ)如图②,点P在外,是的直径,与相切于点B,若,求的大小.
24.如图,有一个圆O和两个正六边形T1,T2. T1的6个顶点都在圆周上,T2的6条边都和圆O相切(我们称T1,T2分别为圆O的内接正六边形和外切正六边形).
(1)设T1,T2的边长分别为a,b,圆O的半径为r,求r:a及r:b的值;
(2)求正六边形T1,T2的面积比S1:S2的值.
参考答案:
1.D
2.D
3.C
4.B
5.C
6.A
7.C
8.A
9.C
10.A
11.
12.
13.30
14.
15.120°
16.①②④
17.
18.
19.45°或135°
20.
21.(1)=70°,=125°;(2)略.
22.(1)略;(2)2+
23.(Ⅰ),;(Ⅱ).
24.(1)1:1,:2(2)3:4
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
