18.2.1矩形 课件
图片预览





文档简介
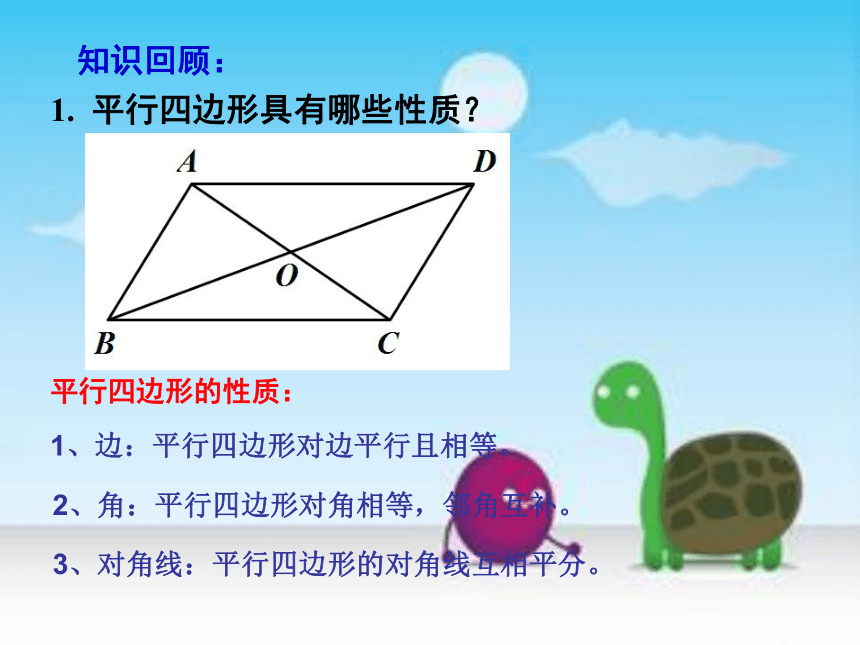
课件27张PPT。知识回顾:1. 平行四边形具有哪些性质?平行四边形的性质:1、边:平行四边形对边平行且相等。2、角:平行四边形对角相等,邻角互补。3、对角线:平行四边形的对角线互相平分。3. 在推动平行四边形的变化过程中,你有没有
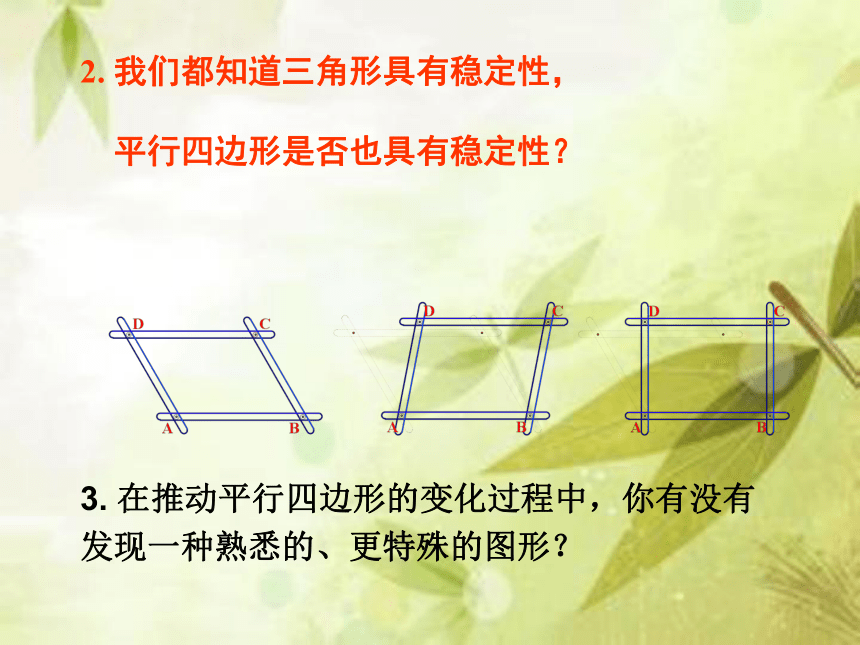
发现一种熟悉的、更特殊的图形?
2. 我们都知道三角形具有稳定性,
平行四边形是否也具有稳定性?
18.2.1 矩形(1)萨拉齐第四中学:郜志雁
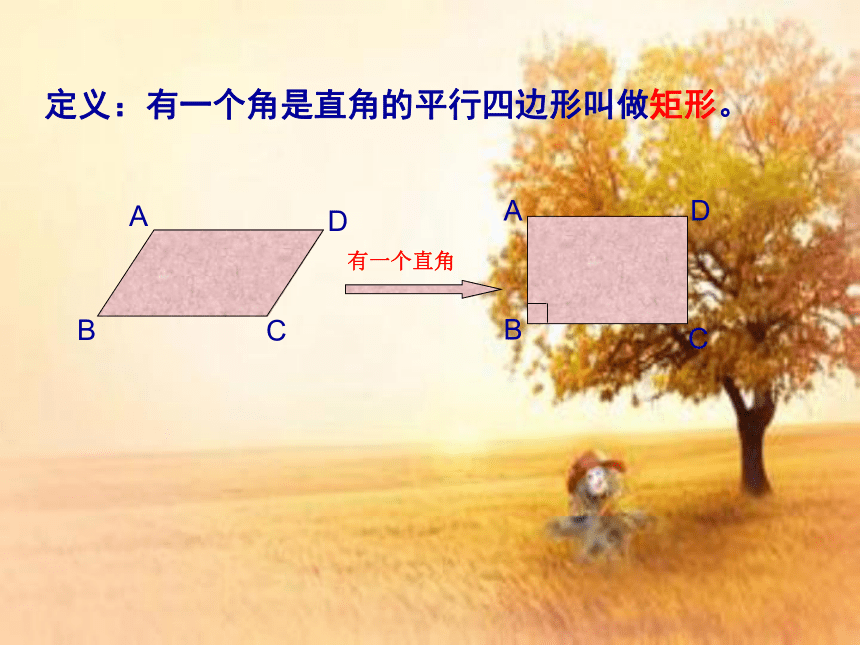
2015.02.18定义:有一个角是直角的平行四边形叫做矩形。有一个直角生活中有很多具有矩形形象的物品,
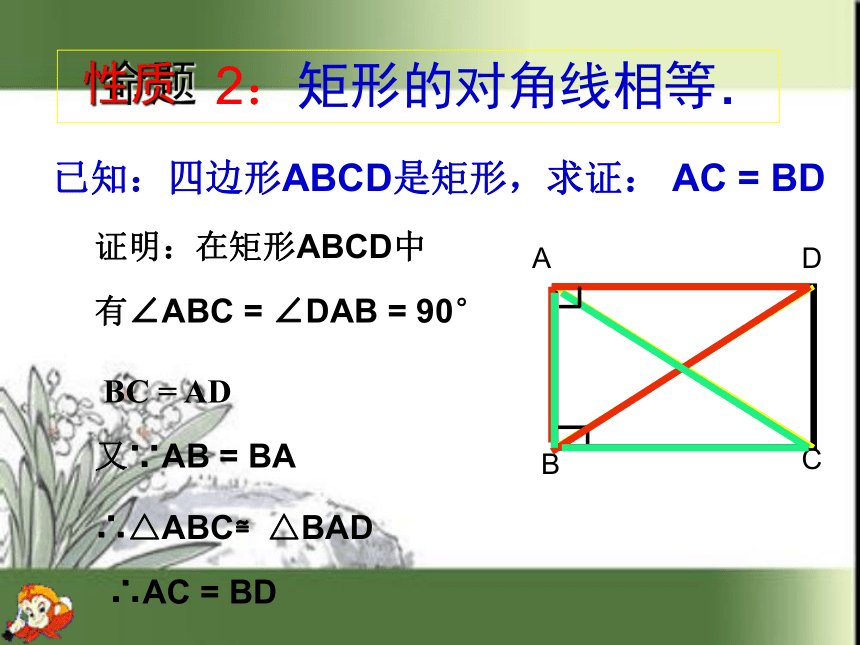
你能举出一些例子吗?说一说,你最牛 思考: 作为特殊的平行四边形,矩形具有平行四边形的所有性质外,还有哪些特殊性质呢?结论1:矩形的四个角都是直角.结论2:矩形的对角线相等.ABCD 1:矩形的四个角都是直角DCBA命题性质 展示你的风采已知:四边形ABCD是矩形,求证: AC = BD 证明:在矩形ABCD中有∠ABC = ∠DAB = 90°
BC = AD又∵AB = BA∴△ABC≌△BAD∴AC = BD 2:矩形的对角线相等.命题性质矩形的性质:1、矩形具有平行四边形的所有性质。
2、矩形的四个角都是直角。
3、矩形的对角线相等。对边平行
且相等四个角
都是直角对角线互相
平分且相等类比总结ODCBA┛在Rt△ABD中,AO是斜边BD的中线直角三角形的性质 :
直角三角形斜边上的中线等于斜边的一半。则有:AO= BD 试试:用文字叙述
直角三角形的性质 在矩形ABCD中
AO=CO=BO=DO= =思考:在Rt△ABD中,AO和BD是什么关系?ACBD
一、小组合作: 小组讨论交流解题思路,小组活动后,小组代表展示活动成果. 1.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,O为对角线AC、BD的交点,且∠CAE=15°,
(1)求证:△AOB为等边三角形;(2)求∠BOE的度数AB=BE OB=BE
∠BOE=∠BEO
又∵∠EBO=∠ABC-∠ABO
=90°-60°=30°
∴∠BOE=°想一想
1.在四边形ABCD中,∠ABC=∠ADC=90°,E是AC的中点,EF平分∠BED交BD于点F。?(1)?猜想:EF与BD具有怎样的关系??(2)?试证明你的猜想。???
?二。跟踪训练2.将矩形纸片ABCD沿对角线BD对折,再折叠使AD与对角线BD重合,得折痕DG,若AB=8,B?C=6,求AG的长。?
解: 矩形纸片ABCD
∠DAB=90°AD=BC, AB=CD
BD= ADG∴挑战开始请 选 择624351挑战第一关进入第二关进入第三关通关小 结(快速问答)1、矩形的定义中有两个条件:
一是:
二是: 有一个角是直角是一个平行四边形(请你的同桌回答)2、矩形具有而一般平行四边形不具有的性质是( )
(A)对角线相等 (B)对边相等
(C)对角相等 (D)对角线互相平分A(请你回答)4、在Rt△ABC中,∠ABC=90°,AC=16,
BO是斜边上的中线,则BO的长为
8(你请他或她回答)3、如图,在矩形ABCD中,对角线AC、BD相交于点O,
且AB=6,BC=8,则△ABO的周长为16(小组讨论完成后汇报。时间:1分钟)5、矩形是轴对称图形吗?它的对称轴是什么?(你请好朋友回答)是对边中点连线所在的直线6、下列说法错误的是( )
(A)矩形的对角线互相平分。
(B)矩形的对角线相等。
(C)有一个角是直角的四边形是矩形。
(D)有一个角是直角的平行四边形叫做矩形。(请你回答)C练习:如图,在矩形ABCD中,AE平分∠BAD,交
BC于点E,ED=5,EC=3,求矩形的周长及对角线的长。
354447挑战第三关 直角三角形性质:直角三角形斜边上的中线
等于斜边的一半.
矩形是轴对称图形,有两条对称轴,连接对边中点
的直线是它的两条对称轴. 课堂小结 1、具有平行四边形的所有性质;
2、矩形的四个角都是直角;
3、矩形的对角线相等且互相平分.矩形:有一个角是直角的平行四边形叫做矩形.作业:教科书第53页练习第2题;
习题18.2第9题.课后作业 再见
发现一种熟悉的、更特殊的图形?
2. 我们都知道三角形具有稳定性,
平行四边形是否也具有稳定性?
18.2.1 矩形(1)萨拉齐第四中学:郜志雁
2015.02.18定义:有一个角是直角的平行四边形叫做矩形。有一个直角生活中有很多具有矩形形象的物品,
你能举出一些例子吗?说一说,你最牛 思考: 作为特殊的平行四边形,矩形具有平行四边形的所有性质外,还有哪些特殊性质呢?结论1:矩形的四个角都是直角.结论2:矩形的对角线相等.ABCD 1:矩形的四个角都是直角DCBA命题性质 展示你的风采已知:四边形ABCD是矩形,求证: AC = BD 证明:在矩形ABCD中有∠ABC = ∠DAB = 90°
BC = AD又∵AB = BA∴△ABC≌△BAD∴AC = BD 2:矩形的对角线相等.命题性质矩形的性质:1、矩形具有平行四边形的所有性质。
2、矩形的四个角都是直角。
3、矩形的对角线相等。对边平行
且相等四个角
都是直角对角线互相
平分且相等类比总结ODCBA┛在Rt△ABD中,AO是斜边BD的中线直角三角形的性质 :
直角三角形斜边上的中线等于斜边的一半。则有:AO= BD 试试:用文字叙述
直角三角形的性质 在矩形ABCD中
AO=CO=BO=DO= =思考:在Rt△ABD中,AO和BD是什么关系?ACBD
一、小组合作: 小组讨论交流解题思路,小组活动后,小组代表展示活动成果. 1.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,O为对角线AC、BD的交点,且∠CAE=15°,
(1)求证:△AOB为等边三角形;(2)求∠BOE的度数AB=BE OB=BE
∠BOE=∠BEO
又∵∠EBO=∠ABC-∠ABO
=90°-60°=30°
∴∠BOE=°想一想
1.在四边形ABCD中,∠ABC=∠ADC=90°,E是AC的中点,EF平分∠BED交BD于点F。?(1)?猜想:EF与BD具有怎样的关系??(2)?试证明你的猜想。???
?二。跟踪训练2.将矩形纸片ABCD沿对角线BD对折,再折叠使AD与对角线BD重合,得折痕DG,若AB=8,B?C=6,求AG的长。?
解: 矩形纸片ABCD
∠DAB=90°AD=BC, AB=CD
BD= ADG∴挑战开始请 选 择624351挑战第一关进入第二关进入第三关通关小 结(快速问答)1、矩形的定义中有两个条件:
一是:
二是: 有一个角是直角是一个平行四边形(请你的同桌回答)2、矩形具有而一般平行四边形不具有的性质是( )
(A)对角线相等 (B)对边相等
(C)对角相等 (D)对角线互相平分A(请你回答)4、在Rt△ABC中,∠ABC=90°,AC=16,
BO是斜边上的中线,则BO的长为
8(你请他或她回答)3、如图,在矩形ABCD中,对角线AC、BD相交于点O,
且AB=6,BC=8,则△ABO的周长为16(小组讨论完成后汇报。时间:1分钟)5、矩形是轴对称图形吗?它的对称轴是什么?(你请好朋友回答)是对边中点连线所在的直线6、下列说法错误的是( )
(A)矩形的对角线互相平分。
(B)矩形的对角线相等。
(C)有一个角是直角的四边形是矩形。
(D)有一个角是直角的平行四边形叫做矩形。(请你回答)C练习:如图,在矩形ABCD中,AE平分∠BAD,交
BC于点E,ED=5,EC=3,求矩形的周长及对角线的长。
354447挑战第三关 直角三角形性质:直角三角形斜边上的中线
等于斜边的一半.
矩形是轴对称图形,有两条对称轴,连接对边中点
的直线是它的两条对称轴. 课堂小结 1、具有平行四边形的所有性质;
2、矩形的四个角都是直角;
3、矩形的对角线相等且互相平分.矩形:有一个角是直角的平行四边形叫做矩形.作业:教科书第53页练习第2题;
习题18.2第9题.课后作业 再见
