3.4 力的合成课件 2023-2024学年高一物理粤教版必修第一册(15张ppt)
文档属性
| 名称 | 3.4 力的合成课件 2023-2024学年高一物理粤教版必修第一册(15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 523.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-11-23 15:14:21 | ||
图片预览





文档简介
(共15张PPT)
第三章 相互作用
第四节 力的合成
现实生活中,物体常常不止受到一个力的作用,如学生背的书包,在公路斜坡上行驶的汽车,建筑工地上几条钢索吊起的重物等,都受到多个力的作用。多个力作用在一个物体上产生的效果能否等效为一个力的作用效果呢?这是本节要学习的内容。
合力与分力
如图所示,提起一桶水,既可以一个成年人单独提,也可以两个孩子一起提,即一个成年人用的力和两个孩子用的力,产生的效果是相同的。这时我们就说,一个成年人用的力和两个孩子用的力是可以互相替代的。替代的前提是等效。
一个成年人与两个孩子分别提同一桶水
如果一个力产生的效果与另外几个力共同作用产生的效果相同,那么这个力与另外几个力等效,可以相互替代,这个力就称为另外几个力的合力,另外几个力称为这个力的分力。
合力和分力的相互替代是一种等效替代。等效替代是重要的科学思维方法之一,它可以使复杂问题变成简单问题。
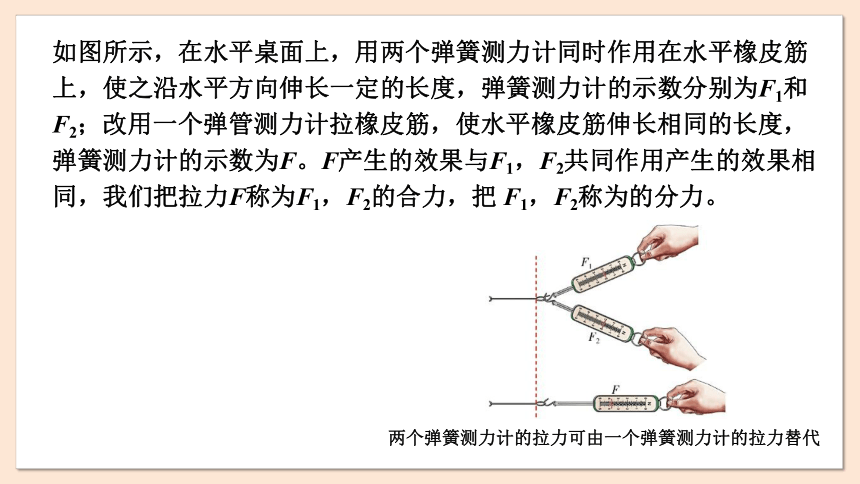
如图所示,在水平桌面上,用两个弹簧测力计同时作用在水平橡皮筋上,使之沿水平方向伸长一定的长度,弹簧测力计的示数分别为F1和 F2;改用一个弹管测力计拉橡皮筋,使水平橡皮筋伸长相同的长度,弹簧测力计的示数为F。F产生的效果与F1,F2共同作用产生的效果相同,我们把拉力F称为F1,F2的合力,把 F1,F2称为的分力。
两个弹簧测力计的拉力可由一个弹簧测力计的拉力替代
力的合成方法
求几个力的合力的过程叫作力的合成。力的合成是一种等效替代的方法,即用一个力去替代几个共同作用的力,替代后产生的效果与原来的相同。
既然合力与分力可以相互替代,那么它们之间存在什么关系呢?
在初中我们已经学过同一直线上两个力的合成方法,现在我们讨论互成角度的力的合成方法。
实验与探究
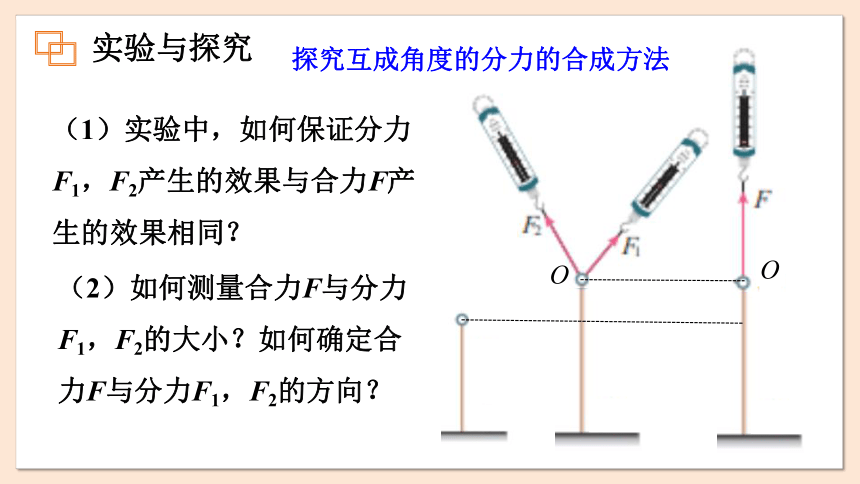
探究互成角度的分力的合成方法
(1)实验中,如何保证分力F1,F2产生的效果与合力F产生的效果相同?
(2)如何测量合力F与分力F1,F2的大小?如何确定合力F与分力F1,F2的方向?
(3)实验过程中需要记录哪些实验数据?
F1,F2,F的方向
O的位置
F1,F2,F的大小
(4)采用什么方法可以直观地描述出力的大小、方向和作用点?
力的图示
?N
【观察】三个力构成什么样的几何图形?
平行四边形
F1与F2为边,F为对角线
如果以表示两个分力的线段为邻边作平行四边形,这两个邻边之间的对角线就表示合力的大小和方向,如图所示。这就是求合力的平行四边形定则。平行四边形定则可应用于合力的计算,其他矢量的合成同样也遵循平行四边形定则。
力的平行四边形定则
合力的计算
物体受到两个力的作用时,根据力的平行四边形定则,可以求出这两个力的合力。
例题:某人水平扔出一个重力 G=0.4 N 的小球,小球在空中受到方向水平向左的风力 F=0.3 N的作用,求球所受的合力。
分析:已知两个力的大小和方向,根据力的平行四边形定则可以求得其合力。
解:①方法一:利用作图法求合力。
用1 cm 长的线段表示0.1 N的力,作出的平行四边形如图所示。用刻度尺量得表示合力F的对角线长 5 cm,所以合力的大小为
F=0.1×5 N=0.5 N,
用量角器量得合力 F与分力 F1的夹角为53°
用作图法求合力
②方法二:利用计算法求合力。
在如图所示的平行四边形中,线段的长度和方向表示力的大小和方向。
根据直角三角形的几何关系,合力的大小为
F== N = 0.5N
合力F与F1的夹角为
tan= = = .
查表,得=53°
用作图法求合力
完成课后相关练习
谢谢观看
谢谢观看
第三章 相互作用
第四节 力的合成
现实生活中,物体常常不止受到一个力的作用,如学生背的书包,在公路斜坡上行驶的汽车,建筑工地上几条钢索吊起的重物等,都受到多个力的作用。多个力作用在一个物体上产生的效果能否等效为一个力的作用效果呢?这是本节要学习的内容。
合力与分力
如图所示,提起一桶水,既可以一个成年人单独提,也可以两个孩子一起提,即一个成年人用的力和两个孩子用的力,产生的效果是相同的。这时我们就说,一个成年人用的力和两个孩子用的力是可以互相替代的。替代的前提是等效。
一个成年人与两个孩子分别提同一桶水
如果一个力产生的效果与另外几个力共同作用产生的效果相同,那么这个力与另外几个力等效,可以相互替代,这个力就称为另外几个力的合力,另外几个力称为这个力的分力。
合力和分力的相互替代是一种等效替代。等效替代是重要的科学思维方法之一,它可以使复杂问题变成简单问题。
如图所示,在水平桌面上,用两个弹簧测力计同时作用在水平橡皮筋上,使之沿水平方向伸长一定的长度,弹簧测力计的示数分别为F1和 F2;改用一个弹管测力计拉橡皮筋,使水平橡皮筋伸长相同的长度,弹簧测力计的示数为F。F产生的效果与F1,F2共同作用产生的效果相同,我们把拉力F称为F1,F2的合力,把 F1,F2称为的分力。
两个弹簧测力计的拉力可由一个弹簧测力计的拉力替代
力的合成方法
求几个力的合力的过程叫作力的合成。力的合成是一种等效替代的方法,即用一个力去替代几个共同作用的力,替代后产生的效果与原来的相同。
既然合力与分力可以相互替代,那么它们之间存在什么关系呢?
在初中我们已经学过同一直线上两个力的合成方法,现在我们讨论互成角度的力的合成方法。
实验与探究
探究互成角度的分力的合成方法
(1)实验中,如何保证分力F1,F2产生的效果与合力F产生的效果相同?
(2)如何测量合力F与分力F1,F2的大小?如何确定合力F与分力F1,F2的方向?
(3)实验过程中需要记录哪些实验数据?
F1,F2,F的方向
O的位置
F1,F2,F的大小
(4)采用什么方法可以直观地描述出力的大小、方向和作用点?
力的图示
?N
【观察】三个力构成什么样的几何图形?
平行四边形
F1与F2为边,F为对角线
如果以表示两个分力的线段为邻边作平行四边形,这两个邻边之间的对角线就表示合力的大小和方向,如图所示。这就是求合力的平行四边形定则。平行四边形定则可应用于合力的计算,其他矢量的合成同样也遵循平行四边形定则。
力的平行四边形定则
合力的计算
物体受到两个力的作用时,根据力的平行四边形定则,可以求出这两个力的合力。
例题:某人水平扔出一个重力 G=0.4 N 的小球,小球在空中受到方向水平向左的风力 F=0.3 N的作用,求球所受的合力。
分析:已知两个力的大小和方向,根据力的平行四边形定则可以求得其合力。
解:①方法一:利用作图法求合力。
用1 cm 长的线段表示0.1 N的力,作出的平行四边形如图所示。用刻度尺量得表示合力F的对角线长 5 cm,所以合力的大小为
F=0.1×5 N=0.5 N,
用量角器量得合力 F与分力 F1的夹角为53°
用作图法求合力
②方法二:利用计算法求合力。
在如图所示的平行四边形中,线段的长度和方向表示力的大小和方向。
根据直角三角形的几何关系,合力的大小为
F== N = 0.5N
合力F与F1的夹角为
tan= = = .
查表,得=53°
用作图法求合力
完成课后相关练习
谢谢观看
谢谢观看
同课章节目录
- 第一章 运动的描述
- 第一节 质点 参考系 时间
- 第二节 位置 位移
- 第三节 速度
- 第四节 测量直线运动物体的瞬时速度
- 第五节 加速度
- 第二章 匀变速直线运动
- 第一节 匀变速直线运动的特点
- 第二节 匀变速直线运动的规律
- 第三节 测量匀变速直线运动的加速度
- 第四节 自由落体运动
- 第五节 匀变速直线运动与汽车安全行驶
- 第三章 相互作用
- 第一节 重力
- 第二节 弹力
- 第三节 摩擦力
- 第四节 力的合成
- 第五节 力的分解
- 第六节 共点力的平衡条件及其应用
- 第四章 牛顿运动定律
- 第一节 牛顿第一定律
- 第二节 加速度与力、质量之间的关系
- 第三节 牛顿第二定律
- 第四节 牛顿第三定律
- 第五节 牛顿运动定律的应用
- 第六节 失重和超重
- 第七节 力学单位
