2023-2024学年黑龙江省哈尔滨市香坊区风华中学九年级(上)期中数学试卷(五四学制)(含解析)
文档属性
| 名称 | 2023-2024学年黑龙江省哈尔滨市香坊区风华中学九年级(上)期中数学试卷(五四学制)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 975.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 19:44:21 | ||
图片预览



文档简介
2023-2024学年黑龙江省哈尔滨市香坊区风华中学九年级(上)期中数学试卷(五四学制)
一、选择题(3×8=24分)
1.(3分)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.(3分)在Rt△ABC中,∠C=90°,,AC=24,则BC的长为( )
A.10 B.24 C.5 D.12
3.(3分)把抛物线先向左平移3个单位再向下平移4个单位,所得到的抛物线是( )
A. B.
C. D.
4.(3分)如图,AB与圆O相切于点A,BO与圆O相交于点C,∠BAC=35°,则∠B的度数为( )
A.20° B.25° C.30° D.35°
5.(3分)如图,把△ABC绕A点顺时针旋转50°,得到△AB'C',若C'B'⊥AB于点E,则∠B'的度数为( )
A.30° B.35° C.40° D.50°
6.(3分)若A(﹣2,y1)、B(﹣3,y2)、C(﹣4,y3)为二次函数的图象上的三点,则y1、y2、y3的大小关系是( )
A.y2<y1<y3 B.y2<y3<y1 C.y3<y1<y2 D.y1<y2<y3
7.(3分)如图,点D、E、F在△ABC的边上,若DE∥BC,EF∥AB,则下列比例式中错误的是( )
A. B. C. D.
8.(3分)下列命题:①一条弧所对的圆周角等于它所对的圆心角的一半;②平分弦的直径垂直于弦,并且平分弦所对的两条弧;③相等的圆心角所对的弧相等,所对的弦也相等;④不在同一直线上的三个点确定一个圆.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题(3×8=24分)
9.(3分)抛物线y=﹣2(x+1)2+3的顶点坐标是 .
10.(3分)在平面直角坐标系中,与点P(2,﹣3)关于原点对称的点的坐标是 .
11.(3分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=4,CD=6,则BC的长为 .
12.(3分)如图,△ADC为⊙O的内接三角形,连接OA、OC,若∠AOC=110°,则∠ADC的度数是 °.
13.(3分)如图,在平行四边形ABCD中,点E在AD上,且AE:ED=3:1,CE的延长线与BA的延长线交于点F,则S△AFE:S△BFC= .
14.(3分)已知⊙O的半径为13cm,弦AB=10cm,弦CD=24cm,且AB∥CD,则AB与CD之间的距离为 cm.
15.(3分)行驶中的汽车遇到紧急情况需急刹车时,行驶路程s(m)与时间t(s)的函数关系式为s=﹣5t2+20t,紧急刹车后由于惯性汽车要滑行 m才能停下来.
16.(3分)如图,BC是半径为5的⊙O的直径,A,D是圆上的两点,AE⊥BC于点E,DF⊥BC于点F,AE=3,DF=4,点P为BC上的一个动点,AP与DE交于点Q,当PA+PD取最小值时,AQ的长为 .
三、解答题(共72分)
17.(8分)先化简,再求代数式的值,其中x=tan60°﹣2sin30°.
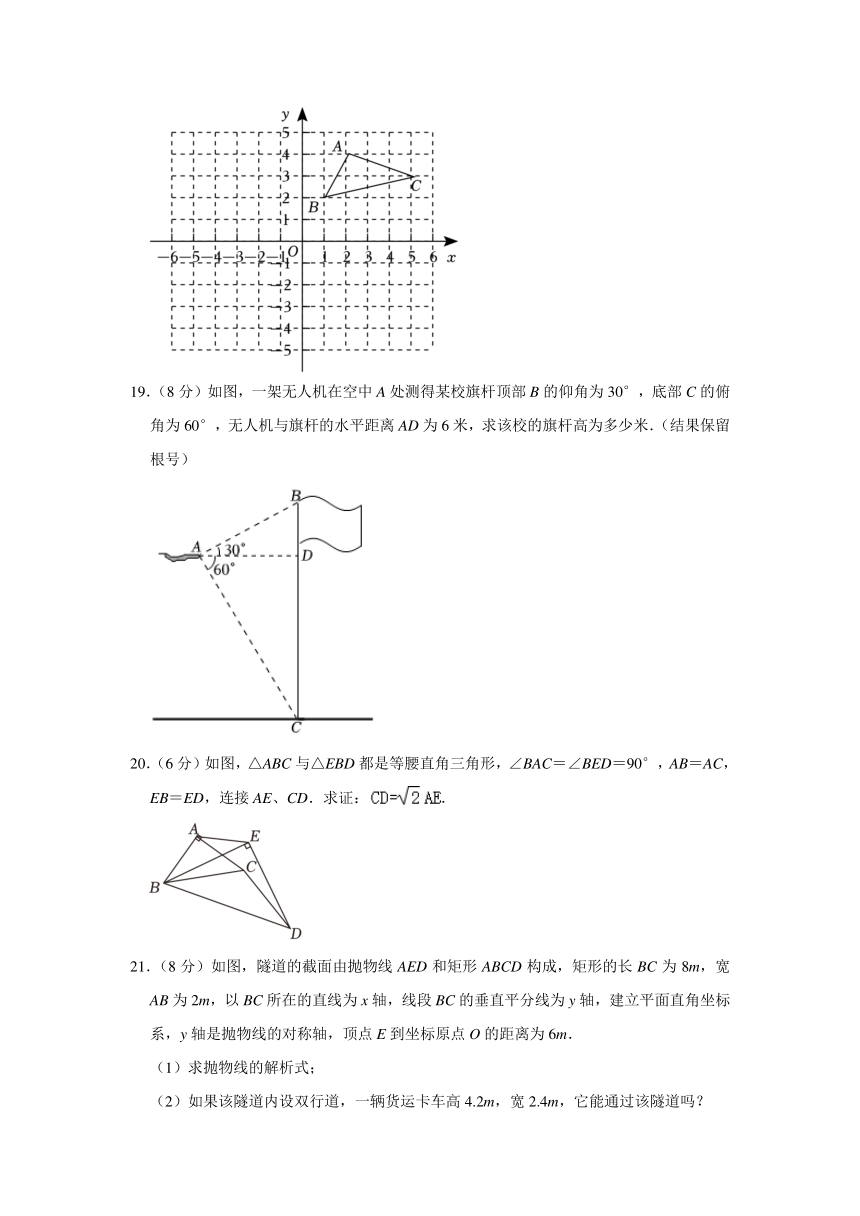
18.(8分)如图,在边长为1的小正方形网格中,△ABC的三个顶点均在格点上,坐标分别为A(2,4),B(1,2),C(5,3).请解答下列问题:
(1)画出△ABC关于y轴的对称图形△A1B1C1;
(2)将△ABC绕点O顺时针旋转90°得到△A2B2C2,画出△A2B2C2;
(3)连接B1B、B1C2,写出∠BB1C2的正切值.
19.(8分)如图,一架无人机在空中A处测得某校旗杆顶部B的仰角为30°,底部C的俯角为60°,无人机与旗杆的水平距离AD为6米,求该校的旗杆高为多少米.(结果保留根号)
20.(6分)如图,△ABC与△EBD都是等腰直角三角形,∠BAC=∠BED=90°,AB=AC,EB=ED,连接AE、CD.求证:.
21.(8分)如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
(1)求抛物线的解析式;
(2)如果该隧道内设双行道,一辆货运卡车高4.2m,宽2.4m,它能通过该隧道吗?
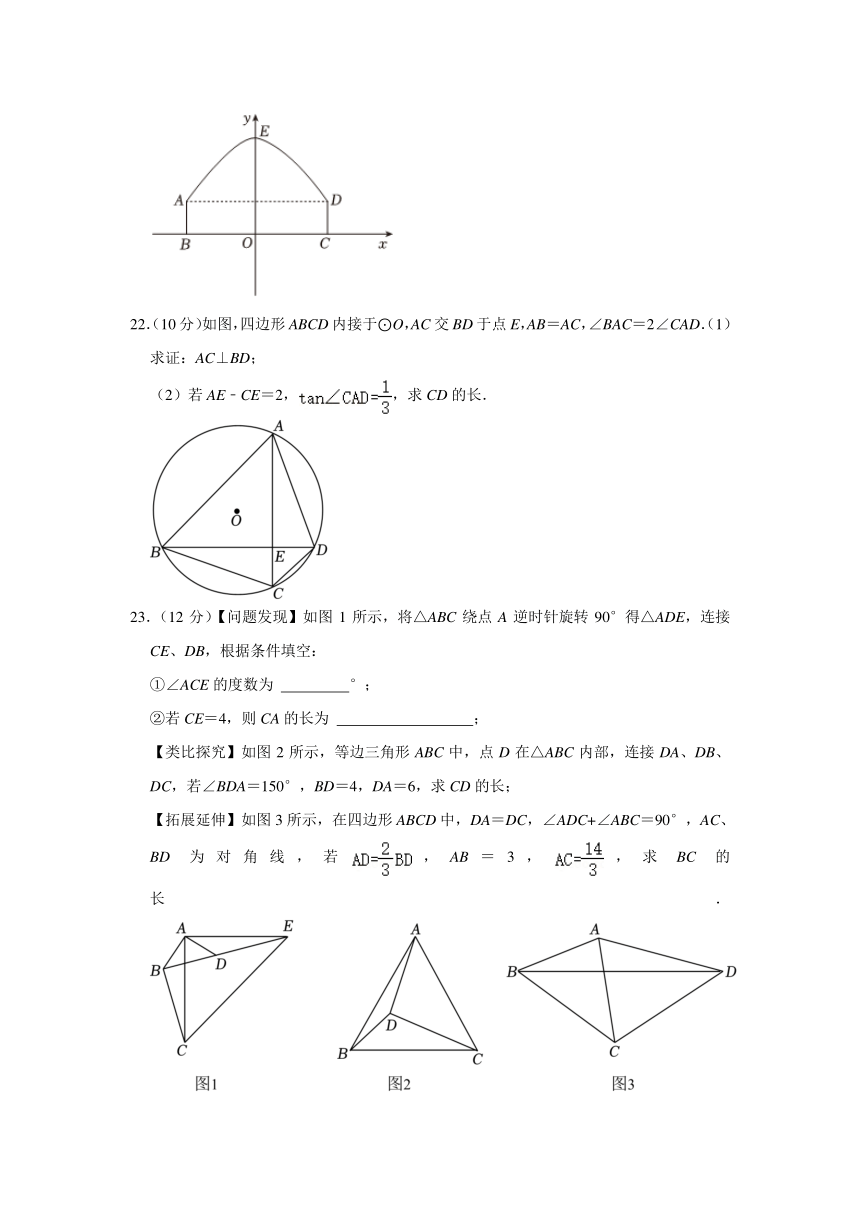
22.(10分)如图,四边形ABCD内接于⊙O,AC交BD于点E,AB=AC,∠BAC=2∠CAD.(1)求证:AC⊥BD;
(2)若AE﹣CE=2,,求CD的长.
23.(12分)【问题发现】如图1所示,将△ABC绕点A逆时针旋转90°得△ADE,连接CE、DB,根据条件填空:
①∠ACE的度数为 °;
②若CE=4,则CA的长为 ;
【类比探究】如图2所示,等边三角形ABC中,点D在△ABC内部,连接DA、DB、DC,若∠BDA=150°,BD=4,DA=6,求CD的长;
【拓展延伸】如图3所示,在四边形ABCD中,DA=DC,∠ADC+∠ABC=90°,AC、BD为对角线,若,AB=3,,求BC的长.
24.(12分)在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2ax﹣3a交x轴的负半轴于点A,交x轴的正半轴点B,交y轴的正半轴于点C,且OB=2OC,点D为抛物线的一点,其横坐标为1.
(1)如图1,求点D的纵坐标;
(2)如图2,点P在第三象限的抛物线上,点P的横坐标为t,连接BP,交y轴于点E,连接CD、DE,设△CDE的面积为S,求S与t之间的函数关系式;
(3)如图3,在(2)的条件下,将线段DE绕点D逆时针旋转90°得到线段DF,射线AE与射线FB交于点G,当EG=BG时,求点E的坐标.
2023-2024学年黑龙江省哈尔滨市香坊区风华中学九年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一、选择题(3×8=24分)
1.(3分)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【分析】根据中心对称图形的定义判断,得到答案.
【解答】解:A、不是轴对称图形,是中心对称图形;
B、是轴对称图形,是中心对称图形;
C、是轴对称图形,不是中心对称图形;
D、是轴对称图形,不是中心对称图形;
故选:B.
【点评】本题考查的是中心对称图形的定义、轴对称图形的定义,把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.
2.(3分)在Rt△ABC中,∠C=90°,,AC=24,则BC的长为( )
A.10 B.24 C.5 D.12
【分析】根据直角三角形的边角关系求出AB,再根据勾股定理求出BC即可.
【解答】解:在Rt△ABC中,∠C=90°,
∵=,AC=24,
∴AB=26,
∴BC==10.
故选:A.
【点评】本题考查解直角三角形,掌握直角三角形的边角关系以及勾股定理是正确解答的前提.
3.(3分)把抛物线先向左平移3个单位再向下平移4个单位,所得到的抛物线是( )
A. B.
C. D.
【分析】根据“左加右减、上加下减”的原则进行解答即可.
【解答】解:把抛物线y=(x﹣4)2先向左平移3个单位,再向下平移4个单位,所得的抛物线的解析式是y=(x﹣4+3)2﹣4,即y=(x﹣1)2﹣4,
故选:D.
【点评】本题主要考查了二次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.
4.(3分)如图,AB与圆O相切于点A,BO与圆O相交于点C,∠BAC=35°,则∠B的度数为( )
A.20° B.25° C.30° D.35°
【分析】由切线的性质可得∠OAB=90°,由∠BAC=35°可得∠OAC=∠OCA=55°,即可求出∠O=70°,进而可求∠B.
【解答】解:∵AB与圆O相切于点A,
∴∠OAB=90°,
∵∠BAC=35°,
∴∠OAC=∠OCA=55°,
∴∠O=70°,
∴∠B=20°.
故选:A.
【点评】本题考查切线的性质,等腰三角形的性质,三角形的内角和,熟练掌握以上知识是解题关键.
5.(3分)如图,把△ABC绕A点顺时针旋转50°,得到△AB'C',若C'B'⊥AB于点E,则∠B'的度数为( )
A.30° B.35° C.40° D.50°
【分析】利用旋转的性质,得到∠BAB'=50°,∠B=∠B',再利用直角三角形两个锐角互余即可得解.
【解答】解:将△ABC绕A点顺时针旋转50°得到△AB'C',
∴∠BAB'=50°,∠B=∠B',
∵B'C'⊥AB,
∴∠B=∠B'=90°﹣∠BAB'=40°;
故选:C.
【点评】本题考查旋转的性质.熟练掌握对应点与旋转中心形成的角为旋转角,对应角相等是解题的关键.
6.(3分)若A(﹣2,y1)、B(﹣3,y2)、C(﹣4,y3)为二次函数的图象上的三点,则y1、y2、y3的大小关系是( )
A.y2<y1<y3 B.y2<y3<y1 C.y3<y1<y2 D.y1<y2<y3
【分析】先求得图象开口方向和对称轴,然后利用二次函数的增减性即可判断.
【解答】解:∵二次函数y=(x+2)2﹣3,
∴开口向上,对称轴为x=﹣2,在对称轴的左侧,y随x的增大而减小,
∵A(﹣2,y1)、B(﹣3,y2)、C(﹣4,y3)为二次函数的图象上的三点,且﹣4<﹣3<﹣2,
∴y1<y2<y3.
故选:D.
【点评】本题考查二次函数图象上点的坐标特征,熟练掌握二次函数的图象及性质,利用函数的增减性解题是关键.
7.(3分)如图,点D、E、F在△ABC的边上,若DE∥BC,EF∥AB,则下列比例式中错误的是( )
A. B. C. D.
【分析】根据平行线分线段成比例定理、相似三角形的判定和性质列出比例式,判断即可.
【解答】解:A、∵DE∥BC,
∴=,本选项比例式正确,不符合题意;
B、∵EF∥AB,
∴=,
∴=,本选项比例式正确,不符合题意;
C、∵DE∥BC,
∴△ADE∽△ABC,
∴=,本选项比例式错误,符合题意;
D、∵EF∥AB,
∴△CEF∽△CAB,
∴=,本选项比例式正确,不符合题意;
故选:C.
【点评】本题考查的是相似三角形的判定和性质、平行线分线段成比例定理,掌握相似三角形的判定定理是解题的关键.
8.(3分)下列命题:①一条弧所对的圆周角等于它所对的圆心角的一半;②平分弦的直径垂直于弦,并且平分弦所对的两条弧;③相等的圆心角所对的弧相等,所对的弦也相等;④不在同一直线上的三个点确定一个圆.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】根据圆周角定理、垂径定理、确定圆的条件判断即可.
【解答】解:①一条弧所对的圆周角等于它所对的圆心角的一半,命题正确;
②平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,故本小题命题错误;
③在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等,故本小题命题错误;
④不在同一直线上的三个点确定一个圆,命题正确;
故选:B.
【点评】本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
二、填空题(3×8=24分)
9.(3分)抛物线y=﹣2(x+1)2+3的顶点坐标是 (﹣1,3) .
【分析】根据顶点式的二次函数解析式,可得二次函数的顶点坐标.
【解答】解:抛物线y=﹣2(x+1)2+3的顶点坐标是 (﹣1,3),
故答案为:(﹣1,3).
【点评】本题考查了二次函数的性质,y=a(x﹣h)2+k的顶点坐标是(h,k).
10.(3分)在平面直角坐标系中,与点P(2,﹣3)关于原点对称的点的坐标是 (﹣2,3) .
【分析】根据关于关于原点对称的点,横坐标与纵坐标都互为相反数,填空即可.
【解答】解:点P(2,﹣3)关于原点对称的点的坐标是(﹣2,3).
故答案为:(﹣2,3).
【点评】本题主要考查了关于原点对称点的性质,掌握好对称点的坐标规律是关键.
11.(3分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=4,CD=6,则BC的长为 3 .
【分析】根据勾股定理得到AC===2,根据余角的性质得到∠ACD=∠B,由相似三角形的性质即可得到结论.
【解答】解:∵CD⊥AB,
∴∠ADC=90°,
∵AD=4,CD=6,
∴AC===2,
∵∠ACB=90°,
∴∠A+∠B=∠A+∠ACD=90°,
∴∠ACD=∠B,
∴△ACD∽△ABC,
∴=,
∴=,
∴BC=3,
故答案为:3.
【点评】本题考查了勾股定理,相似三角形的判定和性质,余角的性质,推出△ACD∽△ABC是解题的关键.
12.(3分)如图,△ADC为⊙O的内接三角形,连接OA、OC,若∠AOC=110°,则∠ADC的度数是 125 °.
【分析】先根据圆周角定理得到∠E,然后根据圆内接四边形的性质得到结论.
【解答】解:如图,在优弧AC上取点E,连接AE,CE,
∵∠AOC=110°,
∴∠E=∠AOC=55°,
∴∠ADC=180°﹣∠E=125°.
故答案为:125.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,也考查了圆内接四边形的性质.
13.(3分)如图,在平行四边形ABCD中,点E在AD上,且AE:ED=3:1,CE的延长线与BA的延长线交于点F,则S△AFE:S△BFC= 9:16 .
【分析】利用平行四边形的性质得出△FAE∽△FBC,进而利用相似三角形的性质得出S△AFE:S△BFC=()2=,进而得出答案.
【解答】解:∵在平行四边形ABCD中,
∴AE∥BC,AD=BC,
∴△FAE∽△FBC,
∵AE:ED=3:1,
∴==,
∴S△AFE:S△BFC=()2=.
故答案为:.
【点评】此题主要考查了平行四边形的性质和相似三角形的判定与性质,得出S△AFE:S△BFC=()2=是解题关键.
14.(3分)已知⊙O的半径为13cm,弦AB=10cm,弦CD=24cm,且AB∥CD,则AB与CD之间的距离为 17或7 cm.
【分析】分两种情况进行讨论:①弦AB和CD在圆心同侧;②弦AB和CD在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可,小心别漏解.
【解答】解:过O作OM⊥AB于M,OM交CD于N,连接OD,OB,
∵AB∥CD,
∴ON⊥CD,
①当弦AB和CD在圆心同侧时,如图,
∵AB=24cm,CD=10cm,ON⊥CD,OM⊥AB,
∴BM=AM=12cm,DN=CN=5cm,
∵OB=OD=13cm,
由勾股定理得:OM===5(cm),
ON===12(cm),
∴MN=12cm﹣5cm=7cm;
②当弦AB和CD在圆心异侧时,如图,
MN=OM+ON=17cm,
所以AB与CD之间的距离为7cm或17cm.
故答案为:17或7.
【点评】本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理以及分类讨论思想的运用.
15.(3分)行驶中的汽车遇到紧急情况需急刹车时,行驶路程s(m)与时间t(s)的函数关系式为s=﹣5t2+20t,紧急刹车后由于惯性汽车要滑行 20 m才能停下来.
【分析】由题意得,此题实际是求从开始刹车到停止所走的路程,即s的最大值.把抛物线解析式化成顶点式后,即可解答.
【解答】解:依题意:该函数关系式化简为s=﹣5(t﹣2)2+20,
当t=2时,汽车停下来,滑行了20m.
故惯性汽车要滑行20米.
故答案为:20.
【点评】本题主要考查二次函数的应用,理解题意得出紧急刹车后由于惯性汽车要滑行的最大距离即为y的最大值是解题的关键.
16.(3分)如图,BC是半径为5的⊙O的直径,A,D是圆上的两点,AE⊥BC于点E,DF⊥BC于点F,AE=3,DF=4,点P为BC上的一个动点,AP与DE交于点Q,当PA+PD取最小值时,AQ的长为 .
【分析】延长DF交⊙于点G,连接OA、OG、PG,则OA=OG=5,∠OEA=∠OFG=90°,BC垂直平分DG,所以GF=DF=4,可求得OE==4,OF==3,连接AG交DE于点I,作AH⊥DF于点H,则AH=EF=7,FH=AE=3,所以GH=GF+FH=7,则AG==7,再证明△AEI∽△GDI,得==,AI=AG=,由PA+PG≥AG,且PG=PD,得PA+PD≥7,所以当点P落在AG上时,PA+PD取得最值7,此时点Q于点I重合,则AQ=AI=,于是得到问题的答案.
【解答】解:延长DF交⊙于点G,连接OA、OG、PG,
∵BC是半径为5的⊙O的直径,AE⊥BC于点E,DF⊥BC于点F,
∴OA=OG=5,∠OEA=∠OFG=90°,BC垂直平分DG,
∵AE=3,DF=4,
∴GF=DF=4,
∴GD=2GF=8,OE===4,OF===3,
连接AG交DE于点I,作AH⊥DF于点H,
∵∠AHF=∠EFH=∠AEF=90°,
∴四边形AEFH是矩形,
∴AH=EF=OE+OF=4+3=7,FH=AE=3,
∴GH=GF+FH=4+3=7,
∴AG===7,
∵AG∥GD,
∴△AEI∽△GDI,
∴==,
∴AI=AG=×7=,
∵PA+PG≥AG,且PG=PD,
∴PA+PD≥7,
∴当点P落在AG上时,PA+PD取得最值7,此时点Q于点I重合,
∴AQ=AI=,
故答案为:.
【点评】此题重点考查垂径定理、勾股定理、线段的垂直平分线的性质、相似三角形的判定与性质、两点之间线段最短等知识,正确地作出所需要的辅助线是解题的关键.
三、解答题(共72分)
17.(8分)先化简,再求代数式的值,其中x=tan60°﹣2sin30°.
【分析】先根据分式的加法法则进行计算,再根据分式的除法法则把除法变成乘法,算乘法,求出x=﹣1,再代入求出答案即可.
【解答】解:
=
=
=,
当x=tan60°﹣2sin30°=﹣2×=﹣1时,
原式=
=
=.
【点评】本题考查了特殊角的三角函数值和分式的化简求值,能正确根据分式的运算法则进行计算是解此题的关键.
18.(8分)如图,在边长为1的小正方形网格中,△ABC的三个顶点均在格点上,坐标分别为A(2,4),B(1,2),C(5,3).请解答下列问题:
(1)画出△ABC关于y轴的对称图形△A1B1C1;
(2)将△ABC绕点O顺时针旋转90°得到△A2B2C2,画出△A2B2C2;
(3)连接B1B、B1C2,写出∠BB1C2的正切值.
【分析】(1)根据轴对称的性质作图即可.
(2)根据旋转的性质作图即可.
(3)根据锐角三角函数的定义计算即可.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)由图可得,tan∠BB1C2=,
∴∠BB1C2的正切值为.
【点评】本题考查作图﹣轴对称变换、旋转变换、解直角三角形,熟练掌握轴对称的性质、旋转的性质、锐角三角函数的定义是解答本题的关键.
19.(8分)如图,一架无人机在空中A处测得某校旗杆顶部B的仰角为30°,底部C的俯角为60°,无人机与旗杆的水平距离AD为6米,求该校的旗杆高为多少米.(结果保留根号)
【分析】分别在Rt△ABD和Rt△ACD中利用锐角三角函数关系得出BD,DC的长,进而求出该旗杆的高度.
【解答】解:在Rt△ABD,
∵AD=6米,∠BAD=30°,
∴tan30°=,
解得:BD=2(米),
在Rt△ACD,
∵AD=6米,∠CAD=60°,
∴tan60°=,
解得:DC=6(米),
故该校的旗杆高约为:BC=BD+DC=2(米),
答:该校的旗杆高为8米.
【点评】本题主要考查解直角三角形的应用﹣仰角俯角问题,熟练掌握直角三角形中锐角三角函数关系是解题关键.
20.(6分)如图,△ABC与△EBD都是等腰直角三角形,∠BAC=∠BED=90°,AB=AC,EB=ED,连接AE、CD.求证:.
【分析】由等腰直角三角形的性质得∠ABC=∠ACB=∠EBC=∠ECB=45°,则∠CBD=∠ABE=45°﹣∠CBE,由勾股定理求得BC=AB,BD=EB,则==,所以△BCD∽△BAE,得==,则CD=AE.
【解答】证明:∵∠BAC=∠BED=90°,AB=AC,EB=ED,
∴∠ABC=∠ACB=∠EBC=∠ECB=45°,
∴∠CBD=∠ABE=45°﹣∠CBE,
∵BC===AB,BD===EB,
∴==,
∴△BCD∽△BAE,
∴==,
∴CD=AE.
【点评】此题重点考查等腰直角三角形的性质、勾股定理、相似三角形的判定与性质等知识,证明△BCD∽△BAE是解题的关键.
21.(8分)如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
(1)求抛物线的解析式;
(2)如果该隧道内设双行道,一辆货运卡车高4.2m,宽2.4m,它能通过该隧道吗?
【分析】(1)根据抛物线在坐标系中的特殊位置,可以设抛物线的一般式,顶点式,求抛物线的解析式;
(2)根据题意,把x=±1.2代入解析式,得到y=5.64.由于5.64>4.2,于是得到货运卡车能通过.
【解答】解:(1)根据题意,A(﹣4,2),D(4,2),E(0,6).
设抛物线的解析式为y=ax2+6(a≠0),把A(﹣4,2)或D(4,2)代入得
16a+6=2.
解得a=﹣,
∴抛物线的解析式为y=﹣x2+6;
(2)根据题意,把x=±2.4代入解析式,得y=4.86.
∵4.86>4.2,
∴货运卡车能通过.
【点评】本题考查了二次函数的应用,运用待定系数法求二次函数的解析式的运用,由函数值求自变量的值的运用,解答时求出二次函数的解析式是关键.
22.(10分)如图,四边形ABCD内接于⊙O,AC交BD于点E,AB=AC,∠BAC=2∠CAD.(1)求证:AC⊥BD;
(2)若AE﹣CE=2,,求CD的长.
【分析】(1)设∠CAD=x,则∠BAC=2x,证明∠CBE+∠BCE=90°即可;
(2)在EA上截取ET,使得ET=CE,设CE=x.利用勾股定理构建方程求解即可.
【解答】(1)证明:设∠CAD=x,则∠BAC=2x,
∴∠CBD=∠CAD=x,
∵AB=AC,
∴∠ACB=∠ABC=(180°﹣2x)=90°﹣x,
∴∠CBE+∠BCE=x+90°﹣x=90°,
∴∠BEC=90°,
∴AC⊥BD;
(2)在EA上截取ET,使得ET=CE,设CE=x.
∵∠CAD=∠CBD,
∴tan∠CBE=tan∠CAD=,
∴==,
∴BE=3x,
∵AE﹣CE=2,
∴AE﹣ET=AT=2,
∴AE=2+x,AB=AC=2x+2,
∵∠AEB=90°,
∴AB2=AE2+BE2,
∴(2x+2)2=(3x)2+(x+2)2,
∴x=或x=0(舍弃),
∴AE=+2=,DE=AE=,
∴CD===.
【点评】本题考查圆周角定理,勾股定理,解直角三角形等知识,解题的关键是学会利用参数构建方程解决问题.
23.(12分)【问题发现】如图1所示,将△ABC绕点A逆时针旋转90°得△ADE,连接CE、DB,根据条件填空:
①∠ACE的度数为 45 °;
②若CE=4,则CA的长为 2 ;
【类比探究】如图2所示,等边三角形ABC中,点D在△ABC内部,连接DA、DB、DC,若∠BDA=150°,BD=4,DA=6,求CD的长;
【拓展延伸】如图3所示,在四边形ABCD中,DA=DC,∠ADC+∠ABC=90°,AC、BD为对角线,若,AB=3,,求BC的长.
【分析】【问题发现】①证△CAE是等腰直角三角形,即可得出答案;
②由等腰直角三角形的性质即可得出结论;
【类比探究】将△ABD绕点A逆时针旋转60°得△ACE,连接DE,则EA=DA,CE=BD=4,∠CEA=∠BDA=150°,∠DAE=60°,证△ADE是等边三角形,得DE=DA=6,∠AED=60°,再证∠CED=90°,即可解决问题;
【拓展延伸】将△ABD绕D逆时针旋转至△ECD,连接BE,则AB=CE=3,BD=ED,∠ADB=∠CDE,∠BAD=∠ECD,再证△ADC∽△BDE,得出BE=7,然后证∠BCE=90°,即可解决问题.
【解答】解:【问题发现】①将△ABC绕点A逆时针旋转90°得△ADE,
∴∠DAB=∠CAE=90°,CA=EA,
∴△CAE是等腰直角三角形,
∴∠ACE=45°,
故答案为:45;
②∵△CAE是等腰直角三角形,
∴AC=CE=×4=2,
故答案为:2;
【类比探究】如图2,将△ABD绕点A逆时针旋转60°得△ACE,连接DE,
由旋转的性质得:EA=DA,CE=BD=4,∠CEA=∠BDA=150°,∠DAE=60°,
∴△ADE是等边三角形,
∴DE=DA=6,∠AED=60°,
∴∠CED=∠CEA﹣∠AED=150°﹣60°=90°,
在Rt△CED中,由勾股定理得:CD===2;
【拓展延伸】如图3,将△ABD绕D逆时针旋转至△ECD,连接BE,
由旋转的性质得:AB=CE=3,BD=ED,∠ADB=∠CDE,∠BAD=∠ECD,
∴∠ADC=∠BDE,
∵DA=DC,
∴==,
又∵∠ADC=∠BDE,
∴△ADC∽△BDE,
∴==,
∴BE=AC=×=7,
∵∠ADC+∠ABC=90°,
∴∠BAD+∠BCD=360°﹣90°=270°,
∵∠BAD=∠ECD,
∴∠ECD+∠BCD=270°,
∴∠BCE=360°﹣270°=90°,
在Rt△BCE中,由勾股定理得:BC===2.
【点评】本题是三角形综合题,考查了旋转的性质、等腰直角三角形的判定与性质、等边三角形的判定与性质、相似三角形的判定与性质以及勾股定理等知识,本题综合性强,熟练掌握旋转的性质和相似三角形的判定与性质是解题的关键,属于中考常考题型.
24.(12分)在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2ax﹣3a交x轴的负半轴于点A,交x轴的正半轴点B,交y轴的正半轴于点C,且OB=2OC,点D为抛物线的一点,其横坐标为1.
(1)如图1,求点D的纵坐标;
(2)如图2,点P在第三象限的抛物线上,点P的横坐标为t,连接BP,交y轴于点E,连接CD、DE,设△CDE的面积为S,求S与t之间的函数关系式;
(3)如图3,在(2)的条件下,将线段DE绕点D逆时针旋转90°得到线段DF,射线AE与射线FB交于点G,当EG=BG时,求点E的坐标.
【分析】(1)由待定系数法即可求解;
(2)由S=CE×xD,即可求解;
(3)证明△END≌△DMF(AAS),得到MF=ND=1,DM=NE=2﹣m,求出点G(,),进而求解.
【解答】解:(1)令y=ax2﹣2ax﹣3a=0,则x=﹣1或3,
即点A、B的坐标分别为:(﹣1,0)、(3,0),
由OB=2OC得,点C(0,),
则﹣3a=,则a=﹣,
则抛物线的表达式为:y=﹣x2+x+;
当x=1时,y=﹣x2+x+=2,即点D(1,2),
即点D纵坐标为2;
(2)设点P(t,﹣t2+t+),
由点P、B的坐标得,直线PB的表达式为:y=﹣(t+1)(x﹣3),
则点E(0,),则CE=﹣=﹣,
则S=CE×xD=﹣t;
(3)由(2)点E(0,),设m=,则点E(0,m),
过点D作y轴的垂线,垂足为点N,交过点F和y轴的平行线于点M,
由题意知,∠EDF=90°,DE=DF,
则∠EDN+∠MDF=90°,
∵∠MDF+∠DFM=90°,
∴∠EDN=∠DFM,
∵∠END=∠DMF=90°,
∴△END≌△DMF(AAS),
∴MF=ND=1,DM=NE=2﹣m,
则点F的坐标为:(,1),
由点B、F的坐标得,直线BF的表达式的表达式为:y=﹣(x﹣3)=﹣(x﹣3)①,
同理可得,直线AE的表达式为:y=m(x+1)②,
联立①②得:﹣(x﹣3)=m(x+1),
解得:x=,则y=,
即点G(,),
令x=,y=,
由点B、E、G的坐标得,EG2=x2+(y﹣m)2,BG2=(x﹣3)2+y2,
∵EG=BG,则x2+(y﹣m)2=(x﹣3)2+y2,
化简得:m4﹣22m2+9=0,
解得:m=﹣+2(不合题意的值已舍去),
即点E(0,﹣+2).
【点评】本题考查了二次函数及其图象性质,三角形全等判定和性质,一次函数的性质等知识,运算能力是解题的关键.
一、选择题(3×8=24分)
1.(3分)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.(3分)在Rt△ABC中,∠C=90°,,AC=24,则BC的长为( )
A.10 B.24 C.5 D.12
3.(3分)把抛物线先向左平移3个单位再向下平移4个单位,所得到的抛物线是( )
A. B.
C. D.
4.(3分)如图,AB与圆O相切于点A,BO与圆O相交于点C,∠BAC=35°,则∠B的度数为( )
A.20° B.25° C.30° D.35°
5.(3分)如图,把△ABC绕A点顺时针旋转50°,得到△AB'C',若C'B'⊥AB于点E,则∠B'的度数为( )
A.30° B.35° C.40° D.50°
6.(3分)若A(﹣2,y1)、B(﹣3,y2)、C(﹣4,y3)为二次函数的图象上的三点,则y1、y2、y3的大小关系是( )
A.y2<y1<y3 B.y2<y3<y1 C.y3<y1<y2 D.y1<y2<y3
7.(3分)如图,点D、E、F在△ABC的边上,若DE∥BC,EF∥AB,则下列比例式中错误的是( )
A. B. C. D.
8.(3分)下列命题:①一条弧所对的圆周角等于它所对的圆心角的一半;②平分弦的直径垂直于弦,并且平分弦所对的两条弧;③相等的圆心角所对的弧相等,所对的弦也相等;④不在同一直线上的三个点确定一个圆.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题(3×8=24分)
9.(3分)抛物线y=﹣2(x+1)2+3的顶点坐标是 .
10.(3分)在平面直角坐标系中,与点P(2,﹣3)关于原点对称的点的坐标是 .
11.(3分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=4,CD=6,则BC的长为 .
12.(3分)如图,△ADC为⊙O的内接三角形,连接OA、OC,若∠AOC=110°,则∠ADC的度数是 °.
13.(3分)如图,在平行四边形ABCD中,点E在AD上,且AE:ED=3:1,CE的延长线与BA的延长线交于点F,则S△AFE:S△BFC= .
14.(3分)已知⊙O的半径为13cm,弦AB=10cm,弦CD=24cm,且AB∥CD,则AB与CD之间的距离为 cm.
15.(3分)行驶中的汽车遇到紧急情况需急刹车时,行驶路程s(m)与时间t(s)的函数关系式为s=﹣5t2+20t,紧急刹车后由于惯性汽车要滑行 m才能停下来.
16.(3分)如图,BC是半径为5的⊙O的直径,A,D是圆上的两点,AE⊥BC于点E,DF⊥BC于点F,AE=3,DF=4,点P为BC上的一个动点,AP与DE交于点Q,当PA+PD取最小值时,AQ的长为 .
三、解答题(共72分)
17.(8分)先化简,再求代数式的值,其中x=tan60°﹣2sin30°.
18.(8分)如图,在边长为1的小正方形网格中,△ABC的三个顶点均在格点上,坐标分别为A(2,4),B(1,2),C(5,3).请解答下列问题:
(1)画出△ABC关于y轴的对称图形△A1B1C1;
(2)将△ABC绕点O顺时针旋转90°得到△A2B2C2,画出△A2B2C2;
(3)连接B1B、B1C2,写出∠BB1C2的正切值.
19.(8分)如图,一架无人机在空中A处测得某校旗杆顶部B的仰角为30°,底部C的俯角为60°,无人机与旗杆的水平距离AD为6米,求该校的旗杆高为多少米.(结果保留根号)
20.(6分)如图,△ABC与△EBD都是等腰直角三角形,∠BAC=∠BED=90°,AB=AC,EB=ED,连接AE、CD.求证:.
21.(8分)如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
(1)求抛物线的解析式;
(2)如果该隧道内设双行道,一辆货运卡车高4.2m,宽2.4m,它能通过该隧道吗?
22.(10分)如图,四边形ABCD内接于⊙O,AC交BD于点E,AB=AC,∠BAC=2∠CAD.(1)求证:AC⊥BD;
(2)若AE﹣CE=2,,求CD的长.
23.(12分)【问题发现】如图1所示,将△ABC绕点A逆时针旋转90°得△ADE,连接CE、DB,根据条件填空:
①∠ACE的度数为 °;
②若CE=4,则CA的长为 ;
【类比探究】如图2所示,等边三角形ABC中,点D在△ABC内部,连接DA、DB、DC,若∠BDA=150°,BD=4,DA=6,求CD的长;
【拓展延伸】如图3所示,在四边形ABCD中,DA=DC,∠ADC+∠ABC=90°,AC、BD为对角线,若,AB=3,,求BC的长.
24.(12分)在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2ax﹣3a交x轴的负半轴于点A,交x轴的正半轴点B,交y轴的正半轴于点C,且OB=2OC,点D为抛物线的一点,其横坐标为1.
(1)如图1,求点D的纵坐标;
(2)如图2,点P在第三象限的抛物线上,点P的横坐标为t,连接BP,交y轴于点E,连接CD、DE,设△CDE的面积为S,求S与t之间的函数关系式;
(3)如图3,在(2)的条件下,将线段DE绕点D逆时针旋转90°得到线段DF,射线AE与射线FB交于点G,当EG=BG时,求点E的坐标.
2023-2024学年黑龙江省哈尔滨市香坊区风华中学九年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一、选择题(3×8=24分)
1.(3分)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【分析】根据中心对称图形的定义判断,得到答案.
【解答】解:A、不是轴对称图形,是中心对称图形;
B、是轴对称图形,是中心对称图形;
C、是轴对称图形,不是中心对称图形;
D、是轴对称图形,不是中心对称图形;
故选:B.
【点评】本题考查的是中心对称图形的定义、轴对称图形的定义,把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.
2.(3分)在Rt△ABC中,∠C=90°,,AC=24,则BC的长为( )
A.10 B.24 C.5 D.12
【分析】根据直角三角形的边角关系求出AB,再根据勾股定理求出BC即可.
【解答】解:在Rt△ABC中,∠C=90°,
∵=,AC=24,
∴AB=26,
∴BC==10.
故选:A.
【点评】本题考查解直角三角形,掌握直角三角形的边角关系以及勾股定理是正确解答的前提.
3.(3分)把抛物线先向左平移3个单位再向下平移4个单位,所得到的抛物线是( )
A. B.
C. D.
【分析】根据“左加右减、上加下减”的原则进行解答即可.
【解答】解:把抛物线y=(x﹣4)2先向左平移3个单位,再向下平移4个单位,所得的抛物线的解析式是y=(x﹣4+3)2﹣4,即y=(x﹣1)2﹣4,
故选:D.
【点评】本题主要考查了二次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.
4.(3分)如图,AB与圆O相切于点A,BO与圆O相交于点C,∠BAC=35°,则∠B的度数为( )
A.20° B.25° C.30° D.35°
【分析】由切线的性质可得∠OAB=90°,由∠BAC=35°可得∠OAC=∠OCA=55°,即可求出∠O=70°,进而可求∠B.
【解答】解:∵AB与圆O相切于点A,
∴∠OAB=90°,
∵∠BAC=35°,
∴∠OAC=∠OCA=55°,
∴∠O=70°,
∴∠B=20°.
故选:A.
【点评】本题考查切线的性质,等腰三角形的性质,三角形的内角和,熟练掌握以上知识是解题关键.
5.(3分)如图,把△ABC绕A点顺时针旋转50°,得到△AB'C',若C'B'⊥AB于点E,则∠B'的度数为( )
A.30° B.35° C.40° D.50°
【分析】利用旋转的性质,得到∠BAB'=50°,∠B=∠B',再利用直角三角形两个锐角互余即可得解.
【解答】解:将△ABC绕A点顺时针旋转50°得到△AB'C',
∴∠BAB'=50°,∠B=∠B',
∵B'C'⊥AB,
∴∠B=∠B'=90°﹣∠BAB'=40°;
故选:C.
【点评】本题考查旋转的性质.熟练掌握对应点与旋转中心形成的角为旋转角,对应角相等是解题的关键.
6.(3分)若A(﹣2,y1)、B(﹣3,y2)、C(﹣4,y3)为二次函数的图象上的三点,则y1、y2、y3的大小关系是( )
A.y2<y1<y3 B.y2<y3<y1 C.y3<y1<y2 D.y1<y2<y3
【分析】先求得图象开口方向和对称轴,然后利用二次函数的增减性即可判断.
【解答】解:∵二次函数y=(x+2)2﹣3,
∴开口向上,对称轴为x=﹣2,在对称轴的左侧,y随x的增大而减小,
∵A(﹣2,y1)、B(﹣3,y2)、C(﹣4,y3)为二次函数的图象上的三点,且﹣4<﹣3<﹣2,
∴y1<y2<y3.
故选:D.
【点评】本题考查二次函数图象上点的坐标特征,熟练掌握二次函数的图象及性质,利用函数的增减性解题是关键.
7.(3分)如图,点D、E、F在△ABC的边上,若DE∥BC,EF∥AB,则下列比例式中错误的是( )
A. B. C. D.
【分析】根据平行线分线段成比例定理、相似三角形的判定和性质列出比例式,判断即可.
【解答】解:A、∵DE∥BC,
∴=,本选项比例式正确,不符合题意;
B、∵EF∥AB,
∴=,
∴=,本选项比例式正确,不符合题意;
C、∵DE∥BC,
∴△ADE∽△ABC,
∴=,本选项比例式错误,符合题意;
D、∵EF∥AB,
∴△CEF∽△CAB,
∴=,本选项比例式正确,不符合题意;
故选:C.
【点评】本题考查的是相似三角形的判定和性质、平行线分线段成比例定理,掌握相似三角形的判定定理是解题的关键.
8.(3分)下列命题:①一条弧所对的圆周角等于它所对的圆心角的一半;②平分弦的直径垂直于弦,并且平分弦所对的两条弧;③相等的圆心角所对的弧相等,所对的弦也相等;④不在同一直线上的三个点确定一个圆.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】根据圆周角定理、垂径定理、确定圆的条件判断即可.
【解答】解:①一条弧所对的圆周角等于它所对的圆心角的一半,命题正确;
②平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,故本小题命题错误;
③在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等,故本小题命题错误;
④不在同一直线上的三个点确定一个圆,命题正确;
故选:B.
【点评】本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
二、填空题(3×8=24分)
9.(3分)抛物线y=﹣2(x+1)2+3的顶点坐标是 (﹣1,3) .
【分析】根据顶点式的二次函数解析式,可得二次函数的顶点坐标.
【解答】解:抛物线y=﹣2(x+1)2+3的顶点坐标是 (﹣1,3),
故答案为:(﹣1,3).
【点评】本题考查了二次函数的性质,y=a(x﹣h)2+k的顶点坐标是(h,k).
10.(3分)在平面直角坐标系中,与点P(2,﹣3)关于原点对称的点的坐标是 (﹣2,3) .
【分析】根据关于关于原点对称的点,横坐标与纵坐标都互为相反数,填空即可.
【解答】解:点P(2,﹣3)关于原点对称的点的坐标是(﹣2,3).
故答案为:(﹣2,3).
【点评】本题主要考查了关于原点对称点的性质,掌握好对称点的坐标规律是关键.
11.(3分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=4,CD=6,则BC的长为 3 .
【分析】根据勾股定理得到AC===2,根据余角的性质得到∠ACD=∠B,由相似三角形的性质即可得到结论.
【解答】解:∵CD⊥AB,
∴∠ADC=90°,
∵AD=4,CD=6,
∴AC===2,
∵∠ACB=90°,
∴∠A+∠B=∠A+∠ACD=90°,
∴∠ACD=∠B,
∴△ACD∽△ABC,
∴=,
∴=,
∴BC=3,
故答案为:3.
【点评】本题考查了勾股定理,相似三角形的判定和性质,余角的性质,推出△ACD∽△ABC是解题的关键.
12.(3分)如图,△ADC为⊙O的内接三角形,连接OA、OC,若∠AOC=110°,则∠ADC的度数是 125 °.
【分析】先根据圆周角定理得到∠E,然后根据圆内接四边形的性质得到结论.
【解答】解:如图,在优弧AC上取点E,连接AE,CE,
∵∠AOC=110°,
∴∠E=∠AOC=55°,
∴∠ADC=180°﹣∠E=125°.
故答案为:125.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,也考查了圆内接四边形的性质.
13.(3分)如图,在平行四边形ABCD中,点E在AD上,且AE:ED=3:1,CE的延长线与BA的延长线交于点F,则S△AFE:S△BFC= 9:16 .
【分析】利用平行四边形的性质得出△FAE∽△FBC,进而利用相似三角形的性质得出S△AFE:S△BFC=()2=,进而得出答案.
【解答】解:∵在平行四边形ABCD中,
∴AE∥BC,AD=BC,
∴△FAE∽△FBC,
∵AE:ED=3:1,
∴==,
∴S△AFE:S△BFC=()2=.
故答案为:.
【点评】此题主要考查了平行四边形的性质和相似三角形的判定与性质,得出S△AFE:S△BFC=()2=是解题关键.
14.(3分)已知⊙O的半径为13cm,弦AB=10cm,弦CD=24cm,且AB∥CD,则AB与CD之间的距离为 17或7 cm.
【分析】分两种情况进行讨论:①弦AB和CD在圆心同侧;②弦AB和CD在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可,小心别漏解.
【解答】解:过O作OM⊥AB于M,OM交CD于N,连接OD,OB,
∵AB∥CD,
∴ON⊥CD,
①当弦AB和CD在圆心同侧时,如图,
∵AB=24cm,CD=10cm,ON⊥CD,OM⊥AB,
∴BM=AM=12cm,DN=CN=5cm,
∵OB=OD=13cm,
由勾股定理得:OM===5(cm),
ON===12(cm),
∴MN=12cm﹣5cm=7cm;
②当弦AB和CD在圆心异侧时,如图,
MN=OM+ON=17cm,
所以AB与CD之间的距离为7cm或17cm.
故答案为:17或7.
【点评】本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理以及分类讨论思想的运用.
15.(3分)行驶中的汽车遇到紧急情况需急刹车时,行驶路程s(m)与时间t(s)的函数关系式为s=﹣5t2+20t,紧急刹车后由于惯性汽车要滑行 20 m才能停下来.
【分析】由题意得,此题实际是求从开始刹车到停止所走的路程,即s的最大值.把抛物线解析式化成顶点式后,即可解答.
【解答】解:依题意:该函数关系式化简为s=﹣5(t﹣2)2+20,
当t=2时,汽车停下来,滑行了20m.
故惯性汽车要滑行20米.
故答案为:20.
【点评】本题主要考查二次函数的应用,理解题意得出紧急刹车后由于惯性汽车要滑行的最大距离即为y的最大值是解题的关键.
16.(3分)如图,BC是半径为5的⊙O的直径,A,D是圆上的两点,AE⊥BC于点E,DF⊥BC于点F,AE=3,DF=4,点P为BC上的一个动点,AP与DE交于点Q,当PA+PD取最小值时,AQ的长为 .
【分析】延长DF交⊙于点G,连接OA、OG、PG,则OA=OG=5,∠OEA=∠OFG=90°,BC垂直平分DG,所以GF=DF=4,可求得OE==4,OF==3,连接AG交DE于点I,作AH⊥DF于点H,则AH=EF=7,FH=AE=3,所以GH=GF+FH=7,则AG==7,再证明△AEI∽△GDI,得==,AI=AG=,由PA+PG≥AG,且PG=PD,得PA+PD≥7,所以当点P落在AG上时,PA+PD取得最值7,此时点Q于点I重合,则AQ=AI=,于是得到问题的答案.
【解答】解:延长DF交⊙于点G,连接OA、OG、PG,
∵BC是半径为5的⊙O的直径,AE⊥BC于点E,DF⊥BC于点F,
∴OA=OG=5,∠OEA=∠OFG=90°,BC垂直平分DG,
∵AE=3,DF=4,
∴GF=DF=4,
∴GD=2GF=8,OE===4,OF===3,
连接AG交DE于点I,作AH⊥DF于点H,
∵∠AHF=∠EFH=∠AEF=90°,
∴四边形AEFH是矩形,
∴AH=EF=OE+OF=4+3=7,FH=AE=3,
∴GH=GF+FH=4+3=7,
∴AG===7,
∵AG∥GD,
∴△AEI∽△GDI,
∴==,
∴AI=AG=×7=,
∵PA+PG≥AG,且PG=PD,
∴PA+PD≥7,
∴当点P落在AG上时,PA+PD取得最值7,此时点Q于点I重合,
∴AQ=AI=,
故答案为:.
【点评】此题重点考查垂径定理、勾股定理、线段的垂直平分线的性质、相似三角形的判定与性质、两点之间线段最短等知识,正确地作出所需要的辅助线是解题的关键.
三、解答题(共72分)
17.(8分)先化简,再求代数式的值,其中x=tan60°﹣2sin30°.
【分析】先根据分式的加法法则进行计算,再根据分式的除法法则把除法变成乘法,算乘法,求出x=﹣1,再代入求出答案即可.
【解答】解:
=
=
=,
当x=tan60°﹣2sin30°=﹣2×=﹣1时,
原式=
=
=.
【点评】本题考查了特殊角的三角函数值和分式的化简求值,能正确根据分式的运算法则进行计算是解此题的关键.
18.(8分)如图,在边长为1的小正方形网格中,△ABC的三个顶点均在格点上,坐标分别为A(2,4),B(1,2),C(5,3).请解答下列问题:
(1)画出△ABC关于y轴的对称图形△A1B1C1;
(2)将△ABC绕点O顺时针旋转90°得到△A2B2C2,画出△A2B2C2;
(3)连接B1B、B1C2,写出∠BB1C2的正切值.
【分析】(1)根据轴对称的性质作图即可.
(2)根据旋转的性质作图即可.
(3)根据锐角三角函数的定义计算即可.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)由图可得,tan∠BB1C2=,
∴∠BB1C2的正切值为.
【点评】本题考查作图﹣轴对称变换、旋转变换、解直角三角形,熟练掌握轴对称的性质、旋转的性质、锐角三角函数的定义是解答本题的关键.
19.(8分)如图,一架无人机在空中A处测得某校旗杆顶部B的仰角为30°,底部C的俯角为60°,无人机与旗杆的水平距离AD为6米,求该校的旗杆高为多少米.(结果保留根号)
【分析】分别在Rt△ABD和Rt△ACD中利用锐角三角函数关系得出BD,DC的长,进而求出该旗杆的高度.
【解答】解:在Rt△ABD,
∵AD=6米,∠BAD=30°,
∴tan30°=,
解得:BD=2(米),
在Rt△ACD,
∵AD=6米,∠CAD=60°,
∴tan60°=,
解得:DC=6(米),
故该校的旗杆高约为:BC=BD+DC=2(米),
答:该校的旗杆高为8米.
【点评】本题主要考查解直角三角形的应用﹣仰角俯角问题,熟练掌握直角三角形中锐角三角函数关系是解题关键.
20.(6分)如图,△ABC与△EBD都是等腰直角三角形,∠BAC=∠BED=90°,AB=AC,EB=ED,连接AE、CD.求证:.
【分析】由等腰直角三角形的性质得∠ABC=∠ACB=∠EBC=∠ECB=45°,则∠CBD=∠ABE=45°﹣∠CBE,由勾股定理求得BC=AB,BD=EB,则==,所以△BCD∽△BAE,得==,则CD=AE.
【解答】证明:∵∠BAC=∠BED=90°,AB=AC,EB=ED,
∴∠ABC=∠ACB=∠EBC=∠ECB=45°,
∴∠CBD=∠ABE=45°﹣∠CBE,
∵BC===AB,BD===EB,
∴==,
∴△BCD∽△BAE,
∴==,
∴CD=AE.
【点评】此题重点考查等腰直角三角形的性质、勾股定理、相似三角形的判定与性质等知识,证明△BCD∽△BAE是解题的关键.
21.(8分)如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
(1)求抛物线的解析式;
(2)如果该隧道内设双行道,一辆货运卡车高4.2m,宽2.4m,它能通过该隧道吗?
【分析】(1)根据抛物线在坐标系中的特殊位置,可以设抛物线的一般式,顶点式,求抛物线的解析式;
(2)根据题意,把x=±1.2代入解析式,得到y=5.64.由于5.64>4.2,于是得到货运卡车能通过.
【解答】解:(1)根据题意,A(﹣4,2),D(4,2),E(0,6).
设抛物线的解析式为y=ax2+6(a≠0),把A(﹣4,2)或D(4,2)代入得
16a+6=2.
解得a=﹣,
∴抛物线的解析式为y=﹣x2+6;
(2)根据题意,把x=±2.4代入解析式,得y=4.86.
∵4.86>4.2,
∴货运卡车能通过.
【点评】本题考查了二次函数的应用,运用待定系数法求二次函数的解析式的运用,由函数值求自变量的值的运用,解答时求出二次函数的解析式是关键.
22.(10分)如图,四边形ABCD内接于⊙O,AC交BD于点E,AB=AC,∠BAC=2∠CAD.(1)求证:AC⊥BD;
(2)若AE﹣CE=2,,求CD的长.
【分析】(1)设∠CAD=x,则∠BAC=2x,证明∠CBE+∠BCE=90°即可;
(2)在EA上截取ET,使得ET=CE,设CE=x.利用勾股定理构建方程求解即可.
【解答】(1)证明:设∠CAD=x,则∠BAC=2x,
∴∠CBD=∠CAD=x,
∵AB=AC,
∴∠ACB=∠ABC=(180°﹣2x)=90°﹣x,
∴∠CBE+∠BCE=x+90°﹣x=90°,
∴∠BEC=90°,
∴AC⊥BD;
(2)在EA上截取ET,使得ET=CE,设CE=x.
∵∠CAD=∠CBD,
∴tan∠CBE=tan∠CAD=,
∴==,
∴BE=3x,
∵AE﹣CE=2,
∴AE﹣ET=AT=2,
∴AE=2+x,AB=AC=2x+2,
∵∠AEB=90°,
∴AB2=AE2+BE2,
∴(2x+2)2=(3x)2+(x+2)2,
∴x=或x=0(舍弃),
∴AE=+2=,DE=AE=,
∴CD===.
【点评】本题考查圆周角定理,勾股定理,解直角三角形等知识,解题的关键是学会利用参数构建方程解决问题.
23.(12分)【问题发现】如图1所示,将△ABC绕点A逆时针旋转90°得△ADE,连接CE、DB,根据条件填空:
①∠ACE的度数为 45 °;
②若CE=4,则CA的长为 2 ;
【类比探究】如图2所示,等边三角形ABC中,点D在△ABC内部,连接DA、DB、DC,若∠BDA=150°,BD=4,DA=6,求CD的长;
【拓展延伸】如图3所示,在四边形ABCD中,DA=DC,∠ADC+∠ABC=90°,AC、BD为对角线,若,AB=3,,求BC的长.
【分析】【问题发现】①证△CAE是等腰直角三角形,即可得出答案;
②由等腰直角三角形的性质即可得出结论;
【类比探究】将△ABD绕点A逆时针旋转60°得△ACE,连接DE,则EA=DA,CE=BD=4,∠CEA=∠BDA=150°,∠DAE=60°,证△ADE是等边三角形,得DE=DA=6,∠AED=60°,再证∠CED=90°,即可解决问题;
【拓展延伸】将△ABD绕D逆时针旋转至△ECD,连接BE,则AB=CE=3,BD=ED,∠ADB=∠CDE,∠BAD=∠ECD,再证△ADC∽△BDE,得出BE=7,然后证∠BCE=90°,即可解决问题.
【解答】解:【问题发现】①将△ABC绕点A逆时针旋转90°得△ADE,
∴∠DAB=∠CAE=90°,CA=EA,
∴△CAE是等腰直角三角形,
∴∠ACE=45°,
故答案为:45;
②∵△CAE是等腰直角三角形,
∴AC=CE=×4=2,
故答案为:2;
【类比探究】如图2,将△ABD绕点A逆时针旋转60°得△ACE,连接DE,
由旋转的性质得:EA=DA,CE=BD=4,∠CEA=∠BDA=150°,∠DAE=60°,
∴△ADE是等边三角形,
∴DE=DA=6,∠AED=60°,
∴∠CED=∠CEA﹣∠AED=150°﹣60°=90°,
在Rt△CED中,由勾股定理得:CD===2;
【拓展延伸】如图3,将△ABD绕D逆时针旋转至△ECD,连接BE,
由旋转的性质得:AB=CE=3,BD=ED,∠ADB=∠CDE,∠BAD=∠ECD,
∴∠ADC=∠BDE,
∵DA=DC,
∴==,
又∵∠ADC=∠BDE,
∴△ADC∽△BDE,
∴==,
∴BE=AC=×=7,
∵∠ADC+∠ABC=90°,
∴∠BAD+∠BCD=360°﹣90°=270°,
∵∠BAD=∠ECD,
∴∠ECD+∠BCD=270°,
∴∠BCE=360°﹣270°=90°,
在Rt△BCE中,由勾股定理得:BC===2.
【点评】本题是三角形综合题,考查了旋转的性质、等腰直角三角形的判定与性质、等边三角形的判定与性质、相似三角形的判定与性质以及勾股定理等知识,本题综合性强,熟练掌握旋转的性质和相似三角形的判定与性质是解题的关键,属于中考常考题型.
24.(12分)在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2ax﹣3a交x轴的负半轴于点A,交x轴的正半轴点B,交y轴的正半轴于点C,且OB=2OC,点D为抛物线的一点,其横坐标为1.
(1)如图1,求点D的纵坐标;
(2)如图2,点P在第三象限的抛物线上,点P的横坐标为t,连接BP,交y轴于点E,连接CD、DE,设△CDE的面积为S,求S与t之间的函数关系式;
(3)如图3,在(2)的条件下,将线段DE绕点D逆时针旋转90°得到线段DF,射线AE与射线FB交于点G,当EG=BG时,求点E的坐标.
【分析】(1)由待定系数法即可求解;
(2)由S=CE×xD,即可求解;
(3)证明△END≌△DMF(AAS),得到MF=ND=1,DM=NE=2﹣m,求出点G(,),进而求解.
【解答】解:(1)令y=ax2﹣2ax﹣3a=0,则x=﹣1或3,
即点A、B的坐标分别为:(﹣1,0)、(3,0),
由OB=2OC得,点C(0,),
则﹣3a=,则a=﹣,
则抛物线的表达式为:y=﹣x2+x+;
当x=1时,y=﹣x2+x+=2,即点D(1,2),
即点D纵坐标为2;
(2)设点P(t,﹣t2+t+),
由点P、B的坐标得,直线PB的表达式为:y=﹣(t+1)(x﹣3),
则点E(0,),则CE=﹣=﹣,
则S=CE×xD=﹣t;
(3)由(2)点E(0,),设m=,则点E(0,m),
过点D作y轴的垂线,垂足为点N,交过点F和y轴的平行线于点M,
由题意知,∠EDF=90°,DE=DF,
则∠EDN+∠MDF=90°,
∵∠MDF+∠DFM=90°,
∴∠EDN=∠DFM,
∵∠END=∠DMF=90°,
∴△END≌△DMF(AAS),
∴MF=ND=1,DM=NE=2﹣m,
则点F的坐标为:(,1),
由点B、F的坐标得,直线BF的表达式的表达式为:y=﹣(x﹣3)=﹣(x﹣3)①,
同理可得,直线AE的表达式为:y=m(x+1)②,
联立①②得:﹣(x﹣3)=m(x+1),
解得:x=,则y=,
即点G(,),
令x=,y=,
由点B、E、G的坐标得,EG2=x2+(y﹣m)2,BG2=(x﹣3)2+y2,
∵EG=BG,则x2+(y﹣m)2=(x﹣3)2+y2,
化简得:m4﹣22m2+9=0,
解得:m=﹣+2(不合题意的值已舍去),
即点E(0,﹣+2).
【点评】本题考查了二次函数及其图象性质,三角形全等判定和性质,一次函数的性质等知识,运算能力是解题的关键.
同课章节目录
