1.1 集合的概念与表示 课件(共70张PPT)
文档属性
| 名称 | 1.1 集合的概念与表示 课件(共70张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 126.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 17:25:26 | ||
图片预览









文档简介
(共70张PPT)
第1章 集 合
1. 1
集合的概念与表示
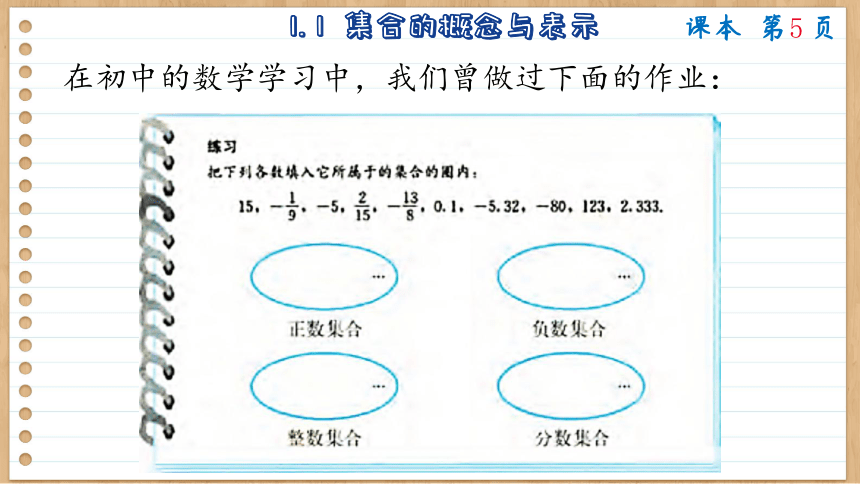
在初中的数学学习中,我们曾做过下面的作业:
5
这里有“正数集合”“负数集合”“整数集合”“分数集合”,那么,
5
● 什么是集合
● 如何用数学语言表示集合
康托尔(G.Cantor,1845—1918),德 国 数学家、集合论创始人,他在 1874 年发表了关于集合论的论文.
5
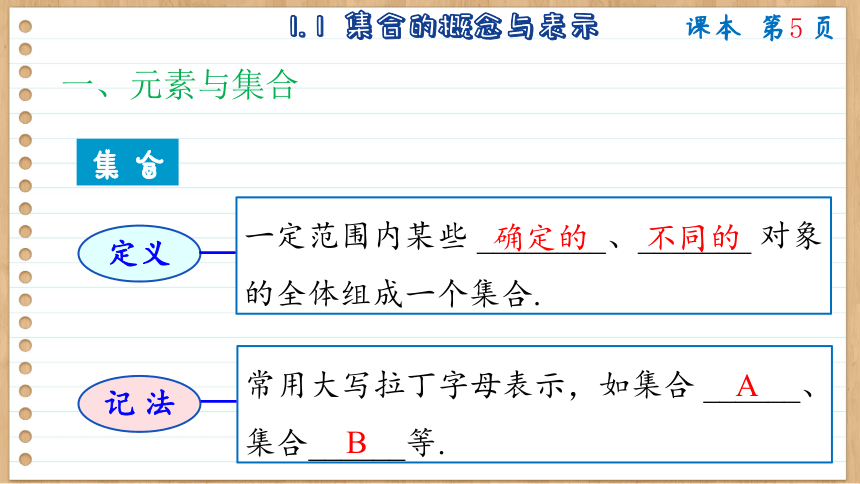
一、元素与集合
集 合
定义
记 法
一定范围内某些 ________、_______ 对象的全体组成一个集合.
确定的
不同的
常用大写拉丁字母表示,如集合 ______、集合______等.
A
B
5
元 素
定义
记 法
集合中的 __________ 称为该集合的元素,简称元.
每一个对象
常用小写的拉丁字母a,b,c,···表示.
5
“中国的直辖市”组成一个集合,该集合的元素就是北京、天津上海和重庆这 4 个城市.
“young 中的字母”组成一个集合,该集合的元素就是 y,o,u,n,g 这5个字母.
“book 中的字母”也组成一个集合,该集合的元素就是 b,o,k 这3个字母.
“1~10 以内的所有质数”组成一个集合,该集合的元素就是 2,3,5,7这4个数.
5
【思考】
(1) 集合中的“研究对象”所指的就是数学中的数、点、
代数式吗
提示:集合中的“研究对象”所指的范围非常广泛,可以是数学中的数、点、代数式,也可以是现实生活中的各种各样的事物或人等.
(2) 根据集合的定义思考:集合中的元素具有哪些特性
提示:确定性、互异性和无序性.
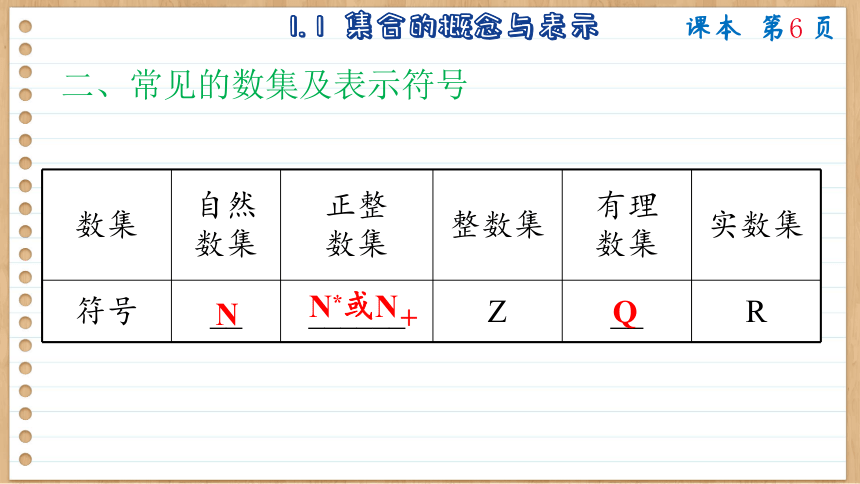
二、常见的数集及表示符号
6
数集 自然数集 正整 数集 整数集 有理 数集 实数集
符号 __ ______ Z __ R
N
N*或N+
Q
6
特别地,全体自然数组成的集合,叫作自然数集,记作 N;
全体正整数组成的集合,叫作正整数集,记作 N*或N+;
全体整数组成的集合,叫作整数集,记作 Z;
全体有理数组成的集合,叫作有理数集,记作 Q;
全体实数组成的集合,叫作实数集,记作 R.
【思考】
N 与 N+ (或N*) 有何区别
提示:N+ (或N*) 是所有正整数组成的集合,而N是由0和所有的正整数组成的集合,所以N比N+ (或N*) 多一个元素0.
三、元素与集合的关系
6
关系 文字叙述 记法 读法
属于 a是集合A的元素 _____ a属于A
不属于 a不是集合A的元素 ____ 或 ______ a不属于A
a∈A
a A
aA
【思考】
元素与集合之间有第三种关系吗
提示:对于一个元素a与一个集合A而言,只有
“a∈A”与“a A”这两种结果.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 在一个集合中可以找到两个相同的元素. ( )
(2) 高中数学新教材苏教版第一册课本上的所有难题能组成集合. ( )
集合中的元素是互不相同的.
“难题”没有严格的标准,所以不能构成集合.
(3) 由方程 x2-4=0和 x-2=0的根组成的集合中有 3个元素. ( )
由于集合中的元素具有互异性,故由两方程的根组成的集合有2个元素.
2. 下列关系中,正确的个数为 ( ).
A. 1 B. 2 C. 3 D. 4
① ∈R. ② Q. ③ |-3|∈N. ④ - ∈Z.
D
【解析】选D. 是实数,是无理数,|-3|=3是非负整数,-=-3是整数,故①②③④均正确.
3. 已知集合 A 含有三个元素0,1,x-2,则实数 x 不能
取的值是________.
【解析】根据集合中元素的互异性可知:
x-2≠0 且 x-2≠1,所以实数 x 不能取的值是 2,3.
2,3
【跟踪训练】
1. 已知 2a∈A,a2-a∈A,若A只含这两个元素,则下列说法中正确的是 ( )
A. a可取全体实数
B. a可取除去0以外的所有实数
C. a可取除去3以外的所有实数
D. a可取除去0和3以外的所有实数
D
解析:因为2a∈A,a2-a∈A,所以2a≠a2-a.
所以a(a-3)≠0.所以a≠0且a≠3.
解析
2. 若以方程 x2-5x+6=0和方程 x2-x-2=0的解为元素的集合为M,则M中元素的个数为 ( )
A.1 B.2 C.3 D.4
解析:方程 x2-5x+6=0 的解为2和3,方程 x2-x-2=0的解为-1和2,所以集合M是由-1,2,3这三个元素组成的集合.
解析
C
3. 英文短语“open the door to...”中的字母构成一个集合,该集合的元素个数是 ( )
A.7 B.8 C.9 D.10
解析:根据集合中元素的互异性可知,“open the door to...”中的不同字母共有“o,p,e,n,t,h,d,r”8个,故该集合的元素个数为 8.
解析
B
4. 下列表述正确的是__________. (填序号)
(1) 0∈N. (2) ∈Z. (3) ∈Z. (4) π Q.
(1),(4)
解析:因为 N、Z、Q 分别表示自然数集、整数集、有理数集. 0是自然数,不是整数, 不是整数,π不是有理数,所以0∈N和π Q正确.
解析
5. 设集合A中含有三个元素3,x,x2-2x.
(1) 求实数x应满足的条件.
解:由集合中元素的互异性可知,x≠3,且
x≠x2-2x,x2-2x≠3.
解之得 x≠-1且 x≠0,且 x≠3.
(2) 若-2∈A,求实数x.
解:因为-2∈A,所以 x=-2 或 x2-2x=-2.
由于 x2-2x= (x-1)2-1≥-1,
所以 x=-2.
【补偿训练】
已知集合A含有两个元素 a-3 和 2a-1,
(1) 若- 3∈A,试求实数a的值.
解:因为-3∈A,所以 a-3=-3或2a-1=-3.
若a-3=-3,则a=0.
此时集合A含有两个元素-3,-1,符合题意.
若 2a-1=-3,则a=-1.
此时集合A含有两个元素-4,-3,符合题意.
综上所述,满足题意的实数a的值为0或-1.
(2) 若a∈A,试求实数a的值.
解:因为a∈A,所以 a-3=a或 2a-1=a.
当 a-3=a 时,有-3=0,不成立.
当2a-1=a时,有a=1,此时A中有两个元素-2,1,符合题意.
综上知 a=1.
1. 列举法
(1) 方法:将集合的元素_________出来,并置于花括
号_________内.
例如{北京,天津,上海,重庆},{y,o,u,n,g}.
(2) 注意事项:①元素之间要用_______分隔;
②列举时与元素的_______无关.
四、集合的表示
6
一一列举
“{ }”
逗号
次序
【思考】
一一列举元素时,需要考虑元素的顺序吗
提示:用列举法表示集合时不必考虑元素的顺序.
例如:{a,b}与 {b,a} 表示同一个集合.
2. 描述法
(1) 形式:{ x∣p(x)},其中x为集合的代表元素,p(x)
指元素 x 具有的性质.
(2) 本质:它是集合符号语言的具体体现,可将集
合中元素的规律与性质清楚地表示出来.
如:{ x∣x 为中国的直辖市,{ x∣x 为 young 中的字母},
{ x∣ x<-3,x ∈ R}.
6
【思考】
{ (x,y) ∣y=x2+2}能否写为{ x∣y=x2+2} 或{ y∣y=x2+2}呢
提示:不能,(x,y) 表示集合的元素是有序实数对或点,而x或y则表示集合的元素是数,所以用描述法表示集合时一定要弄清集合的元素是什么.
3. Venn图法
(1) 形式:画一条封闭的曲线,用它的内部来表示一个集合.
(2) 作用:直观地表示集合.
6
北京,上海,天津,重庆
(1)
y,o,u,n,g
(2)
例如
文恩 ( J . Venn,1834-1923),英国数学家。
例如,由方程 x2-1=0 所有的实数解组成的集合,可以表示为下列形式.
(1) 列举法:{-1,1}(也可以是{1,-1});
一个集合可以用不同的方法表示.
(2) 描述法:{ x∣x2-1=0, x∈R} (也可以是
{ x∣x为方程 x2-1=0 的实数解}).
6
4. 集合相等
(1) 定义:如果两个集合所含的元素完全相同,那么
称这两个集合相等.
(2) 本质:A与B相等,即A中的元素都是B的元素,
B中的元素也都是A的元素.
7
例如,{北京,天津,上海,重庆}
={上海,北京,天津,重庆}.
例 1
用列举法表示下列集合:
7
(1) 大于1且小于 13 的所有偶数组成的集合;
解:设大于1且小于 13 的所有偶数组成的集合为 A,
那么A= {2,4,6,8,10,12}.
(2) 由1~15 以内的所有质数组成的集合.
7
解:设由 1~15 以内的所有质数组成的集合为 B,
那么 B = {2,3,5,7,11,13}.
例 2
用描述法表示下列集合:
7
(1) 大于1的所有偶数组成的集合;
解: 设大于1的偶数为 x,并且满足条件
x>1,x=2k,k∈N,
因此,这个集合表示为
A={ x∣x>1,x=2k,k∈N}.
(2) 不等式 2x-3>5 的解集.
解:由 2x-3>5可得x>4,故不等式2x-3>5的解集
为 { x∣x>4,x∈R }.
7
例1中的集合的元素都有有限个,例2中的集合的元素都有无限个.
五、集合的分类
(1) 含有__________元素的集合称为有限集;
(2) 含有__________元素的集合称为无限集;
(3) _______________的集合称为空集,记作 .
7
有限个
无限个
不含任何元素
【基础小测】
1. 辨析记忆 (对的打“ ”,错的打“ ”).
(1) 由 1,1,2,3 组成的集合可用列举法表示为 {1,1,
2,3}. ( )
(2) 集合{(1,2)}中的元素是1和2. ( )
由1,1,2,3组成的集合可用列举法表示为{1 ,2,3 }.
集合{(1,2)}中的元素是(1,2) .
(3) 集合{ x∣x2=1}与集合{-1,1}相等. ( )
(4) 集合{ x∣x>3} 与集合{ t∣t >3}相等. ( )
由 x2=1求得 x=-1或x=1,所以{ x∣x2=1}与{-1,1}相等.
虽然两个集合的代表元素的符号(字母)不同,但实质上它们均表示大于3的实数,两个集合相等.
2. 给出下列集合,
(1) {0},(2) { x∣x >7,且 x<1},(3){ x∣x>4},
(4) { x∣x2-2=0,x∈Z}.
其中空集的个数为 ( )
A.1 B.2 C.3 D.4
B
3. 由大于-1小于5的自然数组成的集合用列举法表示
为_________________________,用描述法表示为
_______________________________.
{0,1,2,3,4}
{ x ∣ - 1 < x < 5,x∈N}
【题组训练】
1. 已知集合 A= { x∣-1≤x<4,x∈Z},则集合A中元素的个数为 ( )
A.3 B.4 C.5 D.6
C
解析:因为-1≤x<4,x∈Z,所以 x=-1,0,1,2,3,所以集合A= {-1,0,1,2,3}共有5个元素.
解析
2. 集合{(x,y) ∣y=2x-1}表示 ( )
A.方程 y=2x-1
B. 点(x,y)
C. 平面直角坐标系中的点组成的集合
D. 函数 y=2x-1图象上的点组成的集合
D
解析:集合{(x,y) ∣y=2x-1}的代表元素是(x,y),满足的关系式为 y=2x-1,因此集合表示的是函数 y=2x-1图象上的点组成的集合.
解析
3. 已知 a∈ (1,) ,则实数a的值为________.
0
解析:由题意得,a=1或 a= ,
当a=1时,=1 不满足集合中元素的互异性;
当a= 时,a=0 或 a=1,
经检验,a=0 符合题意,综上可知,a=0.
解析
4. 函数 y= 的自变量的值组成的集合为
__________________.
{ x∈R∣x≠1}
解析:函数 y= 的自变量应满足 x≠1,组成的集合用描述法可表示为{ x∈R ∣ x≠1}.
解析
5. 设 x,y 为实数,已知 A= {x,y},B= {0,x2},且
A=B,求 x,y 的值.
解 :因为集合A,B相等,则 x=0或 y=0.
(1)当 x=0时,x2=0,不满足集合中元素的互
异性,故舍去.
(2) 当 y=0时,x=x2,解得x=0 或 x = 1.
由(1)知 x=0 应舍去.
综上知:x=1,y=0.
7
练 习
1. 用“∈”或“ ”填空:
1______N,-3______N,0______N,______N,
1______Z,-3______Q,0______Z, ______R.
∈
∈
∈
∈
∈
∈
7
2. 用列举法表示下列集合 :
(1) { x∣ x + 1 = 0};
解: x+1=0
x =-1.
∴{ x ∣ x+1= 0} ={- 1}
综上所述,结论是:{- 1};
(2) { x∣ x 为15的正约数 };
7
解:15=1×15=3×5.
∴{ x∣x 为15的正约数} ={1,3,5,15}
综上所述,结论是:{1,3,5,15};
(3) { x∣ x为不大于10 的正偶数}.
7
解:不大于10 的正偶数是:2,4,6,8,10
∴ { x∣x 为不大于10的正偶数}
={2,4,6,8,10}
综上所述,结论是:{2,4,6,8,10}.
8
3. 用描述法表示下列集合:
(1) 数的集合;
(2) 正数的集合;
解:奇数的集合= {n=2k-1∣k∈Z};
解:正偶数的集合={z=2k∣ k∈N*};
8
(3) 不等式 x2+1≤0 的解集.
解: x ∈ R,x2≥0,
∴ x2+1≥1,
∴ 不等式 x2+1 < 0的解集为
= { x ∣ x2+1≤0}.
4. 用适当的方法表示下列集合:
8
(1) 方程 x2+2x-15=0 的根的集合;
解:因为方程 x2+2x-15=0的根为 x=-5 或 x=3,
所以方程 x2+2x-15=0 的根的集合为:
{-5,3}.
8
(2) 不等式 4x-3<5的解集.
解:不等式 4x-3<5 的解集为{ x∣x<2}.
8
5. 用列举法表示下列集合:
(1) { a∣0 ≤ a < 6,a∈N };
解:∵0≤a<6 且 a∈N,
∴a = 0,1,2,3,4,5.
∴用列举法表示为{0,1,2,3,4,5}
8
(2) “mathematics 中的字母”组成的集合;
(3) 汉字“永”的笔画组成的集合.
解:∵ mathematics中出现的字母有 a,c,e,h,i,
m,s,t,重复出现的字母只记一次,
∴ 用列举法表示为{a,c,e,h,i,m,s,t};
解:永字的笔画为“、, ,フ, 丿, ”,
∴用列举法表示为{、, ,フ, 丿, ”}.
习题 1.1
感受·理解
1. 用“∈”或“ ”填空:
____Q,π _____ Q, _____ R,+ _____ R.
8
∈
∈
∈
2. 用列举法表示下列集合:
(1) { x | x2 + 3x - 18 = 0,x ∈ R)};
(2) { x | x 为不超过 5 的自然数};
(3) { x | - 3 < 2x-1 ≤3,x ∈ Z};
(4) { (x,y) | 0 ≤ x ≤ 2, 0 ≤ y ≤ 2,x,y ∈ Z};
8
{-6,3}
{0,1,2,3,4,5}
{0,1,2}
{ (0,0),(0,1),(1,0),(1,1),(2,0),(2,1)}
3. 用描述法表示下列集合:
(1) 不等式 3x + 2 > 5 的解集;
(2) 平面直角坐标系中第二象限的点组成的集合;
(3) 二次函数 y = x2-2x+3 图象上的点组成的集合.
8
{x∣3x+2>5} 即{ x∣x >1};
{(x,y) ∣x<0,y>0};
{ (x,y) ∣y=x2-2x+3,x∈R).
思考·运用
4. 用“∈”或“ ”填空:
(1) 若 A= { x∣ x2-x=0},则 1_____A,-1_____A;
(2) 若 B = { x∣1 ≤ x ≤ 5,x∈N},则 1______B,
1.5_____B;
(3) 若 C = { x∣-1< x < 3,x∈Z},则 0.2_____C,
3_____C;
8
∈
∈
5. 设 a,b 为实数,已知 M= {1,2},N={a,b},且
M=N,求 a,b 的值.
8
解:∵ M= {1,2},N= {a,b},且 M=N,
a=1 a=2
∴ 或
b=2 b=1
解:由题意,令 3k+1=-1,解得 k=-,
又∵ K ∈ Z,所以- 1 A.
令 3k+1=5,解得 k=,因为 k∈Z,所以 5∈A.
令 3k+1=7,解得 k=2,因为 k∈Z,所以7∈A.
6. 已知 A= {x∣x=3k+1,k∈Z,问:-1,5,7 三个
数中,哪此数是 A 的元素
8
探究·拓展
7. (写作题) 我们使用符号“e”表短语“是……的元素”
(is an element of). 符号“3∈A”表示“3 是集合 A 的
元素”如果“3 不是集合 A 的元素”,那么写成“3
A”虽然“e”看起来有点像字母“e”,但这两个
符号并不相同,不应混淆.
8
请查阅有关资料,寻找最先引入符号“∈”的数学家,以及符号“∈”的原始意义等信息,写一篇关于符号“∈”的短文.
8
“∈”表示一个元素属于某一集合的记号,是意大利数学学家皮亚诺 (Peano) 在1889年的数学著作中首先使用的.在数系理论研究方面,皮亚诺作出了重大贡献,
在1889年出版的《算术原理新办法》一书中,皮亚诺提出“皮亚诺自然数公理”举世闻名,在书中他还对许多逻辑符号进行了创新.
在1891年创建了《数学杂志》,皮亚诺在这个杂志上利用数理逻辑符号写下自然数公理,并对它们的独立性进行了证明皮亚诺于1893年发表《无穷小分析教程》,该书被德国的数学百科全书列在“自L.欧拉(Euler)和A.L,
柯西(GAUCHY)时代以来最重要的19本微积分教科书”之中.
皮亚诺撰写的《数学百科全书》中有很多地方引人注目,例如推广微分中值定理;多变量函数一致连续性的判定定理;隐函数存在定理以及其可微性定理的证明;部分可微但整体不可微的函数的例子;当时流行的极小理论的反例等.
本课结束
This lesson is over
THANKS!
第1章 集 合
1. 1
集合的概念与表示
在初中的数学学习中,我们曾做过下面的作业:
5
这里有“正数集合”“负数集合”“整数集合”“分数集合”,那么,
5
● 什么是集合
● 如何用数学语言表示集合
康托尔(G.Cantor,1845—1918),德 国 数学家、集合论创始人,他在 1874 年发表了关于集合论的论文.
5
一、元素与集合
集 合
定义
记 法
一定范围内某些 ________、_______ 对象的全体组成一个集合.
确定的
不同的
常用大写拉丁字母表示,如集合 ______、集合______等.
A
B
5
元 素
定义
记 法
集合中的 __________ 称为该集合的元素,简称元.
每一个对象
常用小写的拉丁字母a,b,c,···表示.
5
“中国的直辖市”组成一个集合,该集合的元素就是北京、天津上海和重庆这 4 个城市.
“young 中的字母”组成一个集合,该集合的元素就是 y,o,u,n,g 这5个字母.
“book 中的字母”也组成一个集合,该集合的元素就是 b,o,k 这3个字母.
“1~10 以内的所有质数”组成一个集合,该集合的元素就是 2,3,5,7这4个数.
5
【思考】
(1) 集合中的“研究对象”所指的就是数学中的数、点、
代数式吗
提示:集合中的“研究对象”所指的范围非常广泛,可以是数学中的数、点、代数式,也可以是现实生活中的各种各样的事物或人等.
(2) 根据集合的定义思考:集合中的元素具有哪些特性
提示:确定性、互异性和无序性.
二、常见的数集及表示符号
6
数集 自然数集 正整 数集 整数集 有理 数集 实数集
符号 __ ______ Z __ R
N
N*或N+
Q
6
特别地,全体自然数组成的集合,叫作自然数集,记作 N;
全体正整数组成的集合,叫作正整数集,记作 N*或N+;
全体整数组成的集合,叫作整数集,记作 Z;
全体有理数组成的集合,叫作有理数集,记作 Q;
全体实数组成的集合,叫作实数集,记作 R.
【思考】
N 与 N+ (或N*) 有何区别
提示:N+ (或N*) 是所有正整数组成的集合,而N是由0和所有的正整数组成的集合,所以N比N+ (或N*) 多一个元素0.
三、元素与集合的关系
6
关系 文字叙述 记法 读法
属于 a是集合A的元素 _____ a属于A
不属于 a不是集合A的元素 ____ 或 ______ a不属于A
a∈A
a A
aA
【思考】
元素与集合之间有第三种关系吗
提示:对于一个元素a与一个集合A而言,只有
“a∈A”与“a A”这两种结果.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 在一个集合中可以找到两个相同的元素. ( )
(2) 高中数学新教材苏教版第一册课本上的所有难题能组成集合. ( )
集合中的元素是互不相同的.
“难题”没有严格的标准,所以不能构成集合.
(3) 由方程 x2-4=0和 x-2=0的根组成的集合中有 3个元素. ( )
由于集合中的元素具有互异性,故由两方程的根组成的集合有2个元素.
2. 下列关系中,正确的个数为 ( ).
A. 1 B. 2 C. 3 D. 4
① ∈R. ② Q. ③ |-3|∈N. ④ - ∈Z.
D
【解析】选D. 是实数,是无理数,|-3|=3是非负整数,-=-3是整数,故①②③④均正确.
3. 已知集合 A 含有三个元素0,1,x-2,则实数 x 不能
取的值是________.
【解析】根据集合中元素的互异性可知:
x-2≠0 且 x-2≠1,所以实数 x 不能取的值是 2,3.
2,3
【跟踪训练】
1. 已知 2a∈A,a2-a∈A,若A只含这两个元素,则下列说法中正确的是 ( )
A. a可取全体实数
B. a可取除去0以外的所有实数
C. a可取除去3以外的所有实数
D. a可取除去0和3以外的所有实数
D
解析:因为2a∈A,a2-a∈A,所以2a≠a2-a.
所以a(a-3)≠0.所以a≠0且a≠3.
解析
2. 若以方程 x2-5x+6=0和方程 x2-x-2=0的解为元素的集合为M,则M中元素的个数为 ( )
A.1 B.2 C.3 D.4
解析:方程 x2-5x+6=0 的解为2和3,方程 x2-x-2=0的解为-1和2,所以集合M是由-1,2,3这三个元素组成的集合.
解析
C
3. 英文短语“open the door to...”中的字母构成一个集合,该集合的元素个数是 ( )
A.7 B.8 C.9 D.10
解析:根据集合中元素的互异性可知,“open the door to...”中的不同字母共有“o,p,e,n,t,h,d,r”8个,故该集合的元素个数为 8.
解析
B
4. 下列表述正确的是__________. (填序号)
(1) 0∈N. (2) ∈Z. (3) ∈Z. (4) π Q.
(1),(4)
解析:因为 N、Z、Q 分别表示自然数集、整数集、有理数集. 0是自然数,不是整数, 不是整数,π不是有理数,所以0∈N和π Q正确.
解析
5. 设集合A中含有三个元素3,x,x2-2x.
(1) 求实数x应满足的条件.
解:由集合中元素的互异性可知,x≠3,且
x≠x2-2x,x2-2x≠3.
解之得 x≠-1且 x≠0,且 x≠3.
(2) 若-2∈A,求实数x.
解:因为-2∈A,所以 x=-2 或 x2-2x=-2.
由于 x2-2x= (x-1)2-1≥-1,
所以 x=-2.
【补偿训练】
已知集合A含有两个元素 a-3 和 2a-1,
(1) 若- 3∈A,试求实数a的值.
解:因为-3∈A,所以 a-3=-3或2a-1=-3.
若a-3=-3,则a=0.
此时集合A含有两个元素-3,-1,符合题意.
若 2a-1=-3,则a=-1.
此时集合A含有两个元素-4,-3,符合题意.
综上所述,满足题意的实数a的值为0或-1.
(2) 若a∈A,试求实数a的值.
解:因为a∈A,所以 a-3=a或 2a-1=a.
当 a-3=a 时,有-3=0,不成立.
当2a-1=a时,有a=1,此时A中有两个元素-2,1,符合题意.
综上知 a=1.
1. 列举法
(1) 方法:将集合的元素_________出来,并置于花括
号_________内.
例如{北京,天津,上海,重庆},{y,o,u,n,g}.
(2) 注意事项:①元素之间要用_______分隔;
②列举时与元素的_______无关.
四、集合的表示
6
一一列举
“{ }”
逗号
次序
【思考】
一一列举元素时,需要考虑元素的顺序吗
提示:用列举法表示集合时不必考虑元素的顺序.
例如:{a,b}与 {b,a} 表示同一个集合.
2. 描述法
(1) 形式:{ x∣p(x)},其中x为集合的代表元素,p(x)
指元素 x 具有的性质.
(2) 本质:它是集合符号语言的具体体现,可将集
合中元素的规律与性质清楚地表示出来.
如:{ x∣x 为中国的直辖市,{ x∣x 为 young 中的字母},
{ x∣ x<-3,x ∈ R}.
6
【思考】
{ (x,y) ∣y=x2+2}能否写为{ x∣y=x2+2} 或{ y∣y=x2+2}呢
提示:不能,(x,y) 表示集合的元素是有序实数对或点,而x或y则表示集合的元素是数,所以用描述法表示集合时一定要弄清集合的元素是什么.
3. Venn图法
(1) 形式:画一条封闭的曲线,用它的内部来表示一个集合.
(2) 作用:直观地表示集合.
6
北京,上海,天津,重庆
(1)
y,o,u,n,g
(2)
例如
文恩 ( J . Venn,1834-1923),英国数学家。
例如,由方程 x2-1=0 所有的实数解组成的集合,可以表示为下列形式.
(1) 列举法:{-1,1}(也可以是{1,-1});
一个集合可以用不同的方法表示.
(2) 描述法:{ x∣x2-1=0, x∈R} (也可以是
{ x∣x为方程 x2-1=0 的实数解}).
6
4. 集合相等
(1) 定义:如果两个集合所含的元素完全相同,那么
称这两个集合相等.
(2) 本质:A与B相等,即A中的元素都是B的元素,
B中的元素也都是A的元素.
7
例如,{北京,天津,上海,重庆}
={上海,北京,天津,重庆}.
例 1
用列举法表示下列集合:
7
(1) 大于1且小于 13 的所有偶数组成的集合;
解:设大于1且小于 13 的所有偶数组成的集合为 A,
那么A= {2,4,6,8,10,12}.
(2) 由1~15 以内的所有质数组成的集合.
7
解:设由 1~15 以内的所有质数组成的集合为 B,
那么 B = {2,3,5,7,11,13}.
例 2
用描述法表示下列集合:
7
(1) 大于1的所有偶数组成的集合;
解: 设大于1的偶数为 x,并且满足条件
x>1,x=2k,k∈N,
因此,这个集合表示为
A={ x∣x>1,x=2k,k∈N}.
(2) 不等式 2x-3>5 的解集.
解:由 2x-3>5可得x>4,故不等式2x-3>5的解集
为 { x∣x>4,x∈R }.
7
例1中的集合的元素都有有限个,例2中的集合的元素都有无限个.
五、集合的分类
(1) 含有__________元素的集合称为有限集;
(2) 含有__________元素的集合称为无限集;
(3) _______________的集合称为空集,记作 .
7
有限个
无限个
不含任何元素
【基础小测】
1. 辨析记忆 (对的打“ ”,错的打“ ”).
(1) 由 1,1,2,3 组成的集合可用列举法表示为 {1,1,
2,3}. ( )
(2) 集合{(1,2)}中的元素是1和2. ( )
由1,1,2,3组成的集合可用列举法表示为{1 ,2,3 }.
集合{(1,2)}中的元素是(1,2) .
(3) 集合{ x∣x2=1}与集合{-1,1}相等. ( )
(4) 集合{ x∣x>3} 与集合{ t∣t >3}相等. ( )
由 x2=1求得 x=-1或x=1,所以{ x∣x2=1}与{-1,1}相等.
虽然两个集合的代表元素的符号(字母)不同,但实质上它们均表示大于3的实数,两个集合相等.
2. 给出下列集合,
(1) {0},(2) { x∣x >7,且 x<1},(3){ x∣x>4},
(4) { x∣x2-2=0,x∈Z}.
其中空集的个数为 ( )
A.1 B.2 C.3 D.4
B
3. 由大于-1小于5的自然数组成的集合用列举法表示
为_________________________,用描述法表示为
_______________________________.
{0,1,2,3,4}
{ x ∣ - 1 < x < 5,x∈N}
【题组训练】
1. 已知集合 A= { x∣-1≤x<4,x∈Z},则集合A中元素的个数为 ( )
A.3 B.4 C.5 D.6
C
解析:因为-1≤x<4,x∈Z,所以 x=-1,0,1,2,3,所以集合A= {-1,0,1,2,3}共有5个元素.
解析
2. 集合{(x,y) ∣y=2x-1}表示 ( )
A.方程 y=2x-1
B. 点(x,y)
C. 平面直角坐标系中的点组成的集合
D. 函数 y=2x-1图象上的点组成的集合
D
解析:集合{(x,y) ∣y=2x-1}的代表元素是(x,y),满足的关系式为 y=2x-1,因此集合表示的是函数 y=2x-1图象上的点组成的集合.
解析
3. 已知 a∈ (1,) ,则实数a的值为________.
0
解析:由题意得,a=1或 a= ,
当a=1时,=1 不满足集合中元素的互异性;
当a= 时,a=0 或 a=1,
经检验,a=0 符合题意,综上可知,a=0.
解析
4. 函数 y= 的自变量的值组成的集合为
__________________.
{ x∈R∣x≠1}
解析:函数 y= 的自变量应满足 x≠1,组成的集合用描述法可表示为{ x∈R ∣ x≠1}.
解析
5. 设 x,y 为实数,已知 A= {x,y},B= {0,x2},且
A=B,求 x,y 的值.
解 :因为集合A,B相等,则 x=0或 y=0.
(1)当 x=0时,x2=0,不满足集合中元素的互
异性,故舍去.
(2) 当 y=0时,x=x2,解得x=0 或 x = 1.
由(1)知 x=0 应舍去.
综上知:x=1,y=0.
7
练 习
1. 用“∈”或“ ”填空:
1______N,-3______N,0______N,______N,
1______Z,-3______Q,0______Z, ______R.
∈
∈
∈
∈
∈
∈
7
2. 用列举法表示下列集合 :
(1) { x∣ x + 1 = 0};
解: x+1=0
x =-1.
∴{ x ∣ x+1= 0} ={- 1}
综上所述,结论是:{- 1};
(2) { x∣ x 为15的正约数 };
7
解:15=1×15=3×5.
∴{ x∣x 为15的正约数} ={1,3,5,15}
综上所述,结论是:{1,3,5,15};
(3) { x∣ x为不大于10 的正偶数}.
7
解:不大于10 的正偶数是:2,4,6,8,10
∴ { x∣x 为不大于10的正偶数}
={2,4,6,8,10}
综上所述,结论是:{2,4,6,8,10}.
8
3. 用描述法表示下列集合:
(1) 数的集合;
(2) 正数的集合;
解:奇数的集合= {n=2k-1∣k∈Z};
解:正偶数的集合={z=2k∣ k∈N*};
8
(3) 不等式 x2+1≤0 的解集.
解: x ∈ R,x2≥0,
∴ x2+1≥1,
∴ 不等式 x2+1 < 0的解集为
= { x ∣ x2+1≤0}.
4. 用适当的方法表示下列集合:
8
(1) 方程 x2+2x-15=0 的根的集合;
解:因为方程 x2+2x-15=0的根为 x=-5 或 x=3,
所以方程 x2+2x-15=0 的根的集合为:
{-5,3}.
8
(2) 不等式 4x-3<5的解集.
解:不等式 4x-3<5 的解集为{ x∣x<2}.
8
5. 用列举法表示下列集合:
(1) { a∣0 ≤ a < 6,a∈N };
解:∵0≤a<6 且 a∈N,
∴a = 0,1,2,3,4,5.
∴用列举法表示为{0,1,2,3,4,5}
8
(2) “mathematics 中的字母”组成的集合;
(3) 汉字“永”的笔画组成的集合.
解:∵ mathematics中出现的字母有 a,c,e,h,i,
m,s,t,重复出现的字母只记一次,
∴ 用列举法表示为{a,c,e,h,i,m,s,t};
解:永字的笔画为“、, ,フ, 丿, ”,
∴用列举法表示为{、, ,フ, 丿, ”}.
习题 1.1
感受·理解
1. 用“∈”或“ ”填空:
____Q,π _____ Q, _____ R,+ _____ R.
8
∈
∈
∈
2. 用列举法表示下列集合:
(1) { x | x2 + 3x - 18 = 0,x ∈ R)};
(2) { x | x 为不超过 5 的自然数};
(3) { x | - 3 < 2x-1 ≤3,x ∈ Z};
(4) { (x,y) | 0 ≤ x ≤ 2, 0 ≤ y ≤ 2,x,y ∈ Z};
8
{-6,3}
{0,1,2,3,4,5}
{0,1,2}
{ (0,0),(0,1),(1,0),(1,1),(2,0),(2,1)}
3. 用描述法表示下列集合:
(1) 不等式 3x + 2 > 5 的解集;
(2) 平面直角坐标系中第二象限的点组成的集合;
(3) 二次函数 y = x2-2x+3 图象上的点组成的集合.
8
{x∣3x+2>5} 即{ x∣x >1};
{(x,y) ∣x<0,y>0};
{ (x,y) ∣y=x2-2x+3,x∈R).
思考·运用
4. 用“∈”或“ ”填空:
(1) 若 A= { x∣ x2-x=0},则 1_____A,-1_____A;
(2) 若 B = { x∣1 ≤ x ≤ 5,x∈N},则 1______B,
1.5_____B;
(3) 若 C = { x∣-1< x < 3,x∈Z},则 0.2_____C,
3_____C;
8
∈
∈
5. 设 a,b 为实数,已知 M= {1,2},N={a,b},且
M=N,求 a,b 的值.
8
解:∵ M= {1,2},N= {a,b},且 M=N,
a=1 a=2
∴ 或
b=2 b=1
解:由题意,令 3k+1=-1,解得 k=-,
又∵ K ∈ Z,所以- 1 A.
令 3k+1=5,解得 k=,因为 k∈Z,所以 5∈A.
令 3k+1=7,解得 k=2,因为 k∈Z,所以7∈A.
6. 已知 A= {x∣x=3k+1,k∈Z,问:-1,5,7 三个
数中,哪此数是 A 的元素
8
探究·拓展
7. (写作题) 我们使用符号“e”表短语“是……的元素”
(is an element of). 符号“3∈A”表示“3 是集合 A 的
元素”如果“3 不是集合 A 的元素”,那么写成“3
A”虽然“e”看起来有点像字母“e”,但这两个
符号并不相同,不应混淆.
8
请查阅有关资料,寻找最先引入符号“∈”的数学家,以及符号“∈”的原始意义等信息,写一篇关于符号“∈”的短文.
8
“∈”表示一个元素属于某一集合的记号,是意大利数学学家皮亚诺 (Peano) 在1889年的数学著作中首先使用的.在数系理论研究方面,皮亚诺作出了重大贡献,
在1889年出版的《算术原理新办法》一书中,皮亚诺提出“皮亚诺自然数公理”举世闻名,在书中他还对许多逻辑符号进行了创新.
在1891年创建了《数学杂志》,皮亚诺在这个杂志上利用数理逻辑符号写下自然数公理,并对它们的独立性进行了证明皮亚诺于1893年发表《无穷小分析教程》,该书被德国的数学百科全书列在“自L.欧拉(Euler)和A.L,
柯西(GAUCHY)时代以来最重要的19本微积分教科书”之中.
皮亚诺撰写的《数学百科全书》中有很多地方引人注目,例如推广微分中值定理;多变量函数一致连续性的判定定理;隐函数存在定理以及其可微性定理的证明;部分可微但整体不可微的函数的例子;当时流行的极小理论的反例等.
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
