17.1勾股定理课件
图片预览




文档简介
课件31张PPT。17.1.1勾股定理勾股定理弦图 这个图形里 到底蕴涵了什么样博大精深的知识呢?
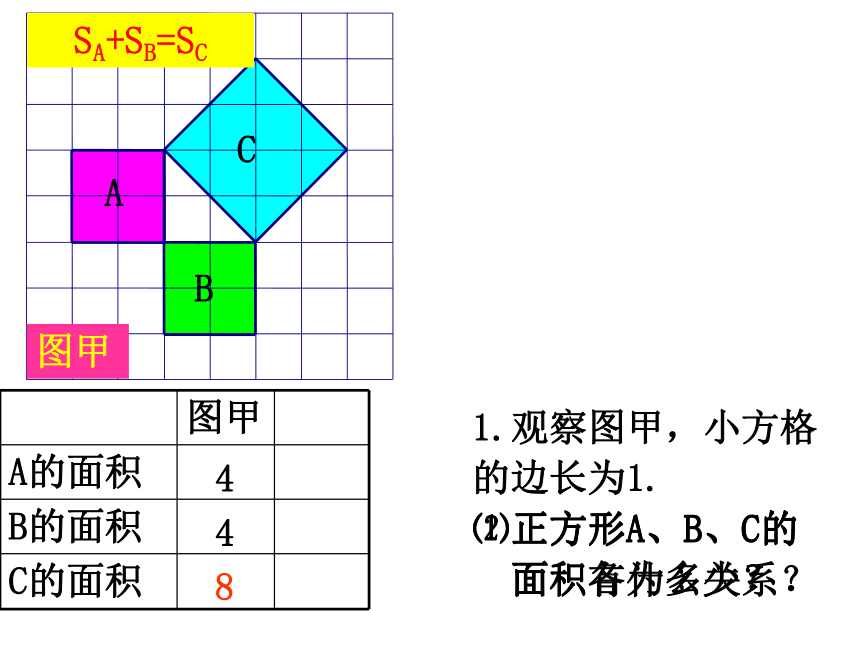
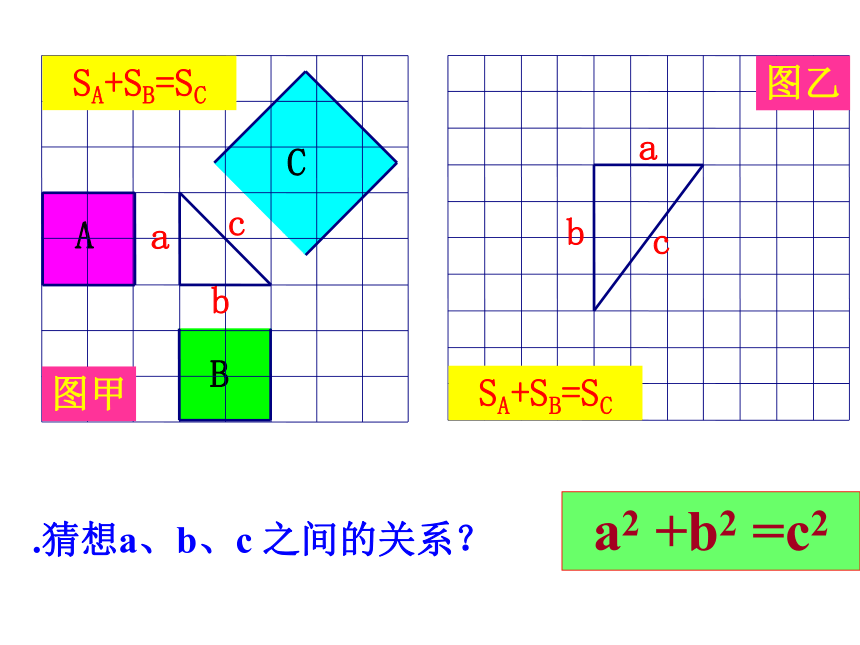
它标志着我国古代数学的成就!448SA+SB=SCC图甲1.观察图甲,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?⑵正方形A、B、C的
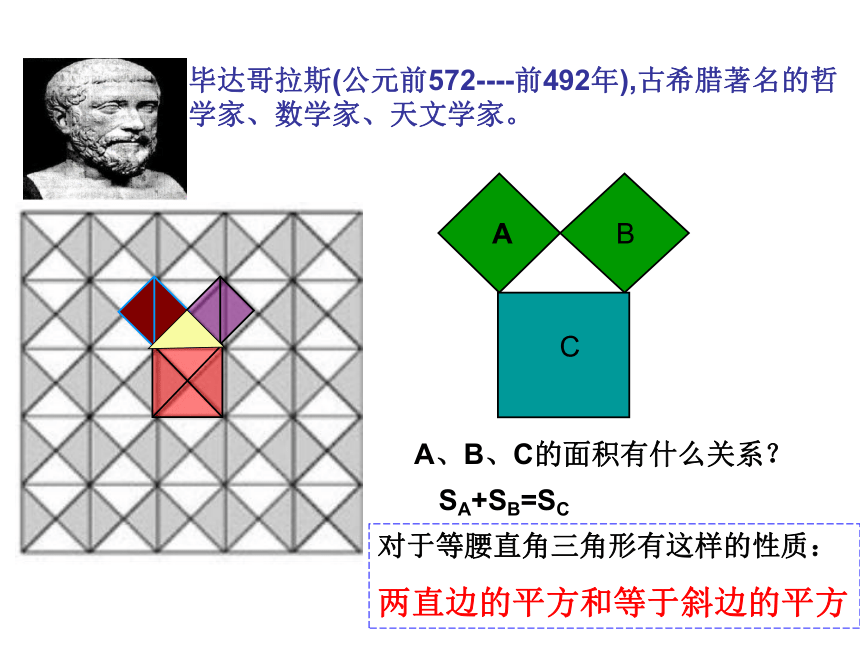
面积有什么关系?毕达哥拉斯(公元前572----前492年),古希腊著名的哲学家、数学家、天文学家。A、B、C的面积有什么关系?SA+SB=SC对于等腰直角三角形有这样的性质:
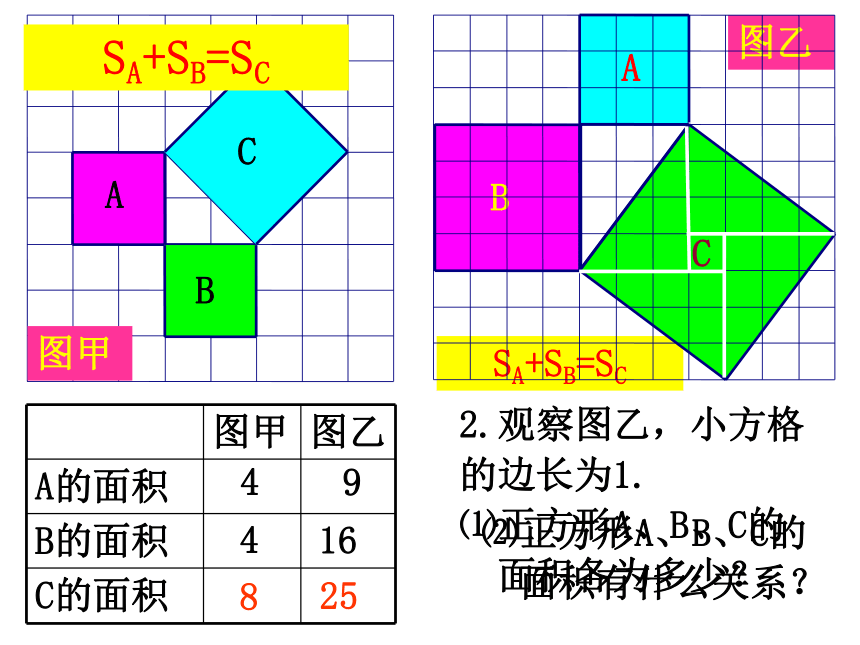
两直边的平方和等于斜边的平方C图乙2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?91625SA+SB=SC⑵正方形A、B、C的
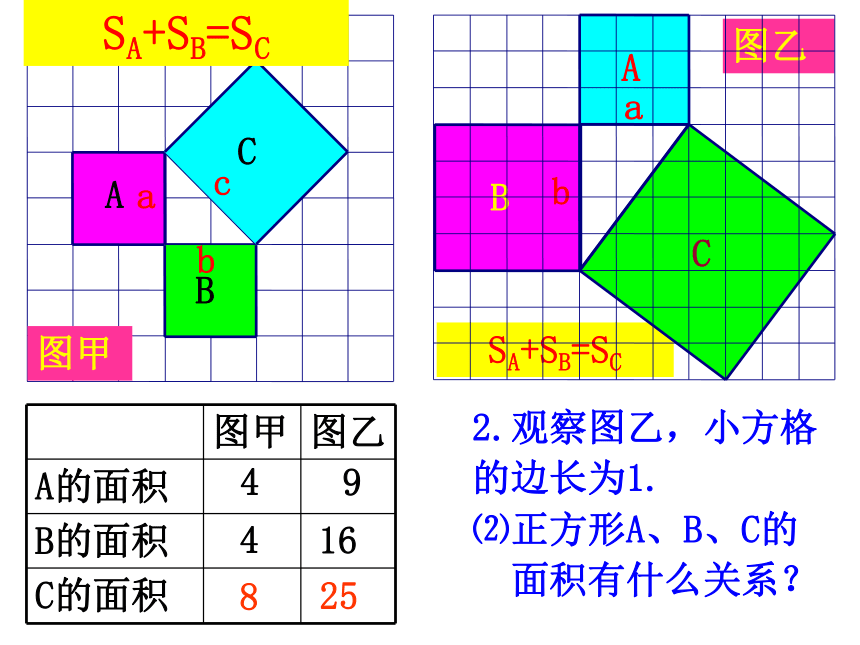
面积有什么关系?448图甲SA+SB=SC图乙2.观察图乙,小方格
的边长为1.91625SA+SB=SC⑵正方形A、B、C的
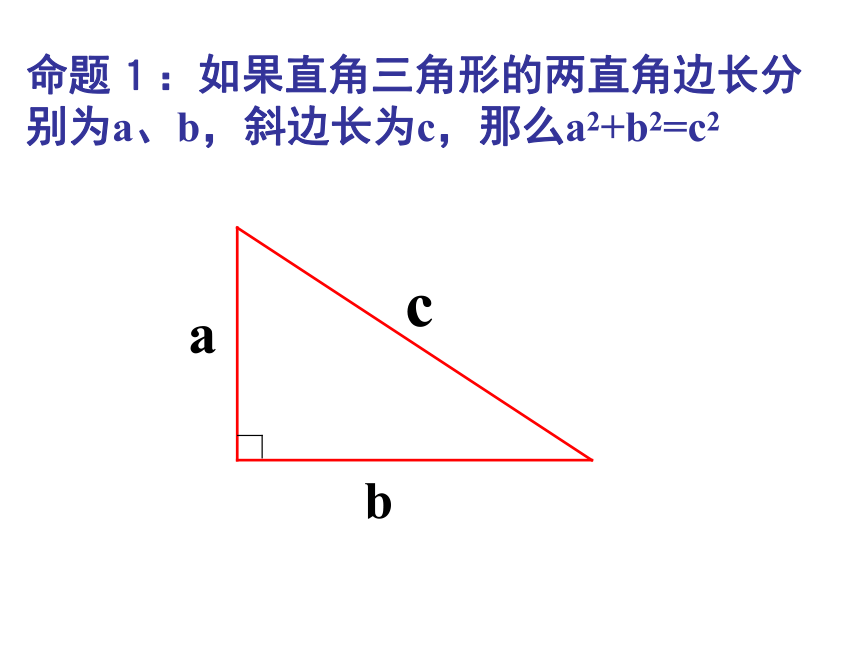
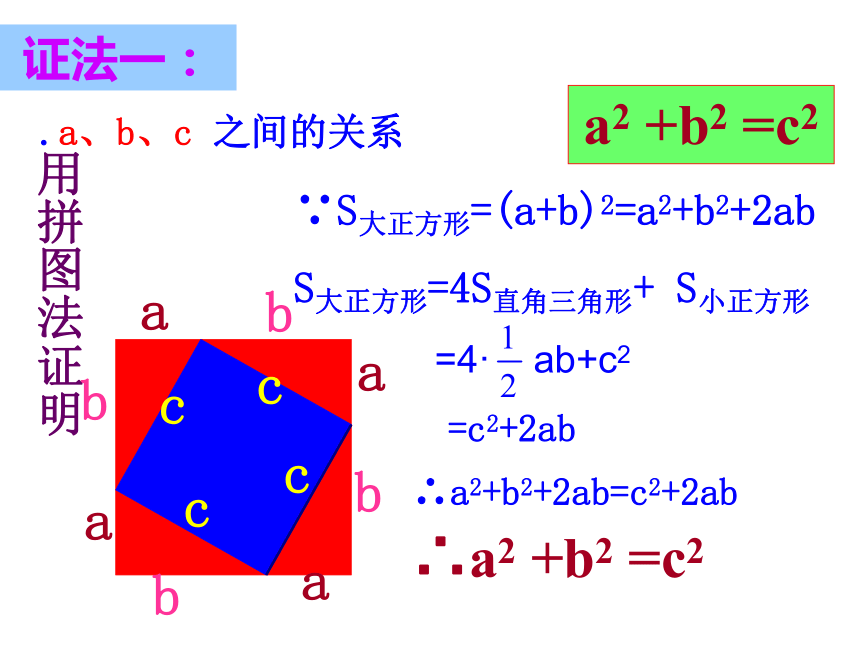
面积有什么关系?448图甲abcabcSA+SB=SC.猜想a、b、c 之间的关系?a2 +b2 =c2命题1:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2用拼图法证明∵S大正方形=(a+b)2=a2+b2+2ab
S大正方形=4S直角三角形+ S小正方形
=4· ab+c2
=c2+2ab
∴a2+b2+2ab=c2+2ab∴a2 +b2 =c2证法一:abcS大正方形=c2S小正方形=(b-a)2S大正方形=4·S三角形+S小正方形弦图 现在我们一起来探索“弦图”的奥妙吧!证法二:baa经过证明被确认正确的命题叫做定理.用赵爽弦图证明勾股定理=1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第二十任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统”证法。 美国总统的证明证法三:aabbcc伽菲尔德证法:∴ a2 + b2 = c2 勾股定理(gou-gu法则)如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cba公式变形c2=a2 + b2a2=c2-b2b2 =c2-a2课堂 练 习1、求下图中字母所代表的正方形的面积。225400A81225B6251442.求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做3、求出下列直角三角形中未知边的长度比一比看看谁算得快!4.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x5.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49 练习2 如图,所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D 的边长分别是12,16,9,12.求最大正方形E 的面积. 通过这种方法,
可以把一个正方形
的面积分成若干
个小正方形的面积的和,不断地分下去,
就可以得到一棵美丽的勾股树.请谈谈你的收获1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为( )A.3 米 B.4 米 C.5米 D.6米C345 或 2、已知:Rt△ABC中,AB=4,AC=3,则BC的长为___________ .试一试:3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )2、4、6C 4、6、8B试一试:B 6、8、10D 8、10、124、湖的两端有A、B两点,从与BA方向成直角的公元前方向上的点C测得CA=130米,CB=120米,则AB为( ) A.50米 B.120米 C.100米 D.130米130120?A1、判断题:
1)直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a2+b2 =c2( )
2) 直角三角形的两边长分别是3和4,则第三边长是5.
( )
××能力比拼
它标志着我国古代数学的成就!448SA+SB=SCC图甲1.观察图甲,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?⑵正方形A、B、C的
面积有什么关系?毕达哥拉斯(公元前572----前492年),古希腊著名的哲学家、数学家、天文学家。A、B、C的面积有什么关系?SA+SB=SC对于等腰直角三角形有这样的性质:
两直边的平方和等于斜边的平方C图乙2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?91625SA+SB=SC⑵正方形A、B、C的
面积有什么关系?448图甲SA+SB=SC图乙2.观察图乙,小方格
的边长为1.91625SA+SB=SC⑵正方形A、B、C的
面积有什么关系?448图甲abcabcSA+SB=SC.猜想a、b、c 之间的关系?a2 +b2 =c2命题1:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2用拼图法证明∵S大正方形=(a+b)2=a2+b2+2ab
S大正方形=4S直角三角形+ S小正方形
=4· ab+c2
=c2+2ab
∴a2+b2+2ab=c2+2ab∴a2 +b2 =c2证法一:abcS大正方形=c2S小正方形=(b-a)2S大正方形=4·S三角形+S小正方形弦图 现在我们一起来探索“弦图”的奥妙吧!证法二:baa经过证明被确认正确的命题叫做定理.用赵爽弦图证明勾股定理=1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第二十任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统”证法。 美国总统的证明证法三:aabbcc伽菲尔德证法:∴ a2 + b2 = c2 勾股定理(gou-gu法则)如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cba公式变形c2=a2 + b2a2=c2-b2b2 =c2-a2课堂 练 习1、求下图中字母所代表的正方形的面积。225400A81225B6251442.求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做3、求出下列直角三角形中未知边的长度比一比看看谁算得快!4.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x5.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49 练习2 如图,所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D 的边长分别是12,16,9,12.求最大正方形E 的面积. 通过这种方法,
可以把一个正方形
的面积分成若干
个小正方形的面积的和,不断地分下去,
就可以得到一棵美丽的勾股树.请谈谈你的收获1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为( )A.3 米 B.4 米 C.5米 D.6米C345 或 2、已知:Rt△ABC中,AB=4,AC=3,则BC的长为___________ .试一试:3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )2、4、6C 4、6、8B试一试:B 6、8、10D 8、10、124、湖的两端有A、B两点,从与BA方向成直角的公元前方向上的点C测得CA=130米,CB=120米,则AB为( ) A.50米 B.120米 C.100米 D.130米130120?A1、判断题:
1)直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a2+b2 =c2( )
2) 直角三角形的两边长分别是3和4,则第三边长是5.
( )
××能力比拼
