3.3中心对称课件

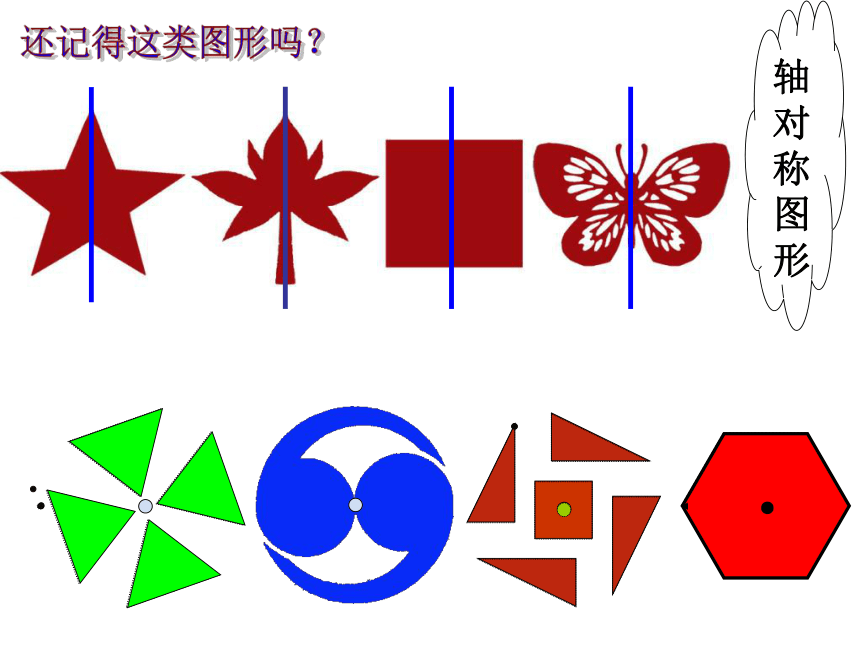
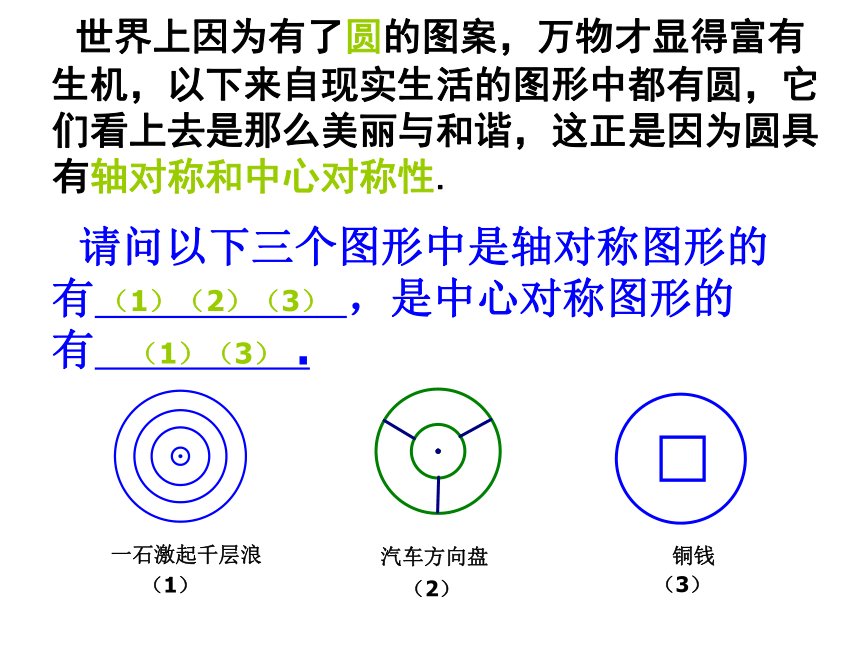
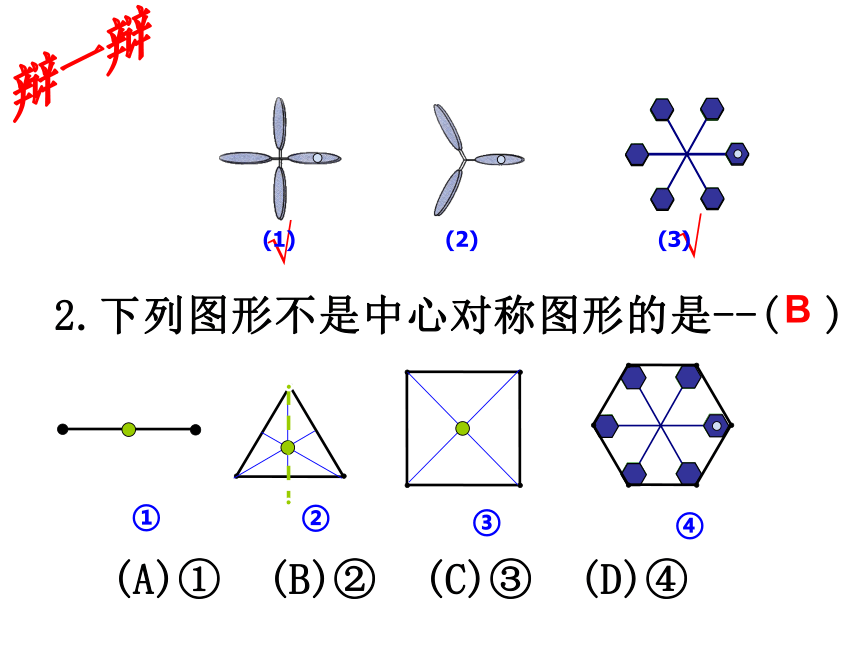
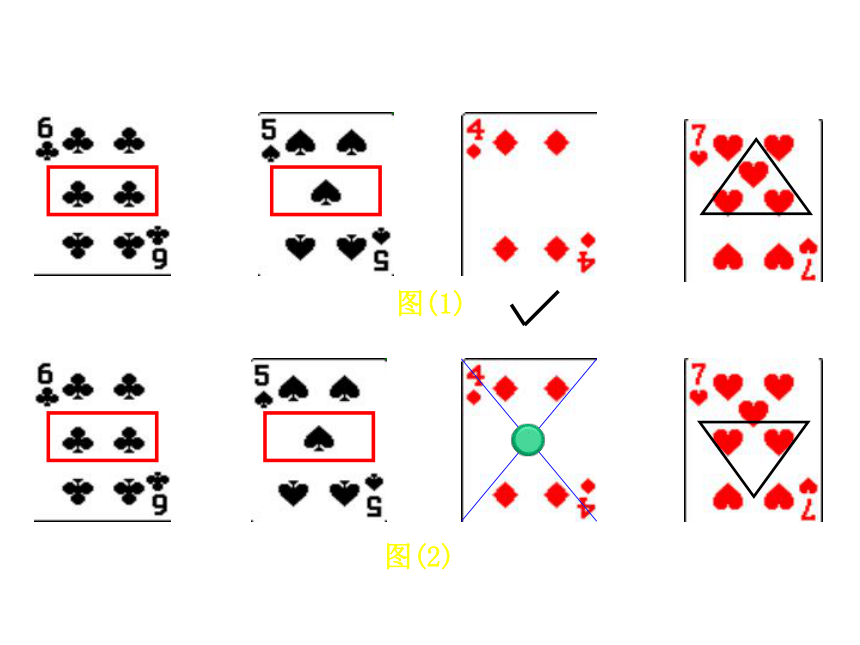
课件33张PPT。中心对称图形风车太极图飞机的螺旋桨图中的图形有怎样的特点呢？风车太极图飞机的螺旋桨新知识 如果一个图形绕着一个点旋转180°，所得到的图形能够和原来的图形互相重合，那么这个图形叫做中心对称图形.轴对称图形还记得这类图形吗？中心对称图形与轴对称图形有哪些区别？● 世界上因为有了圆的图案，万物才显得富有生机，以下来自现实生活的图形中都有圆，它们看上去是那么美丽与和谐，这正是因为圆具有轴对称和中心对称性. 请问以下三个图形中是轴对称图形的有 ，是中心对称图形的有 .一石激起千层浪汽车方向盘铜钱（1）（2）（3）（1）（2）（3）（1）（3）1.下面哪个图形是中心对称图形？辩一辩√√(1)(2)(3)B 如图（1）所示，魔术师把4张扑克牌放在桌子上，然后蒙住眼睛，请一位观众上台，把某一张牌旋转180°，魔术师解除蒙面后，看到4张扑克牌如图（2）所示，他很快确定了哪一张牌被旋转过，你能吗？图(1)图(2)生活中的数学图(1)图(2)解密魔术A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z 在26个英文大写正体字母中,哪些字母是中心对称图形?
A B C D E F G H I J K L M
N O P Q R S T U V W X Y ZA B C D E F G H I J K L M
N O P Q R S T U V W X Y Z英文字母中的数学2018/12/15中心对称的特征与实际应用具有数学美。因为中心对称图形形状匀称美观。所以许多建筑、工艺品、商标常用这种图形作装饰图案。
平稳旋转。具有中心对称图形形状的物体，能够在所在的平面内绕对称中心平稳旋转。所以在生产中，有关旋转的零部件常设计成中心对称图形。自由创作 结合本节课所学知识，发挥你的才华，请创作一幅有关“中心对称”的图形…请以给定的图形○○△△＝(两个圆,两个三角形,两条平行线)为构件,尽可能多地构思有意义的一些中心对称或轴对称图形,并写上一两句贴切,诙谐的解说词.如下图就是符合要求的图形,你能构思其它图形吗?比一比,看谁想得多,看谁想得妙!路灯与倒影指南针除号沙漏两只拔河的小鸡应用新知应用一：画出已知图形关于某一点的对称图形AO1、已知点A和点O，画出点A关于点O的对称点A ′2、已知线段AB和点O，画出线段AB关于点O的对称图形OB ′A′应用新知应用二：判断两个全等的图形是否关于某一点对称试着做做请画出△ABC绕点O按顺时针方向旋转180°后的图形？ABCOA ′B ′C ′如果一个图形绕某一点旋转180°后能与另一个图形重合，那么这两个图形就叫做关于这个点对称，简称中心对称 。这个点叫做这两个图形的对称中心。中心对称的两个图形中的对应点、对应线段，分别叫做关于对称中心的对称点、对称线段。一起探究 1、△ABC与△A ′ B ′ C ′是关于点O对称的两个三角形，连结各对对应点，你发现了什么？
2、你认为OA与OA ′，OB与OB ′，OC与OC ′具有怎样的关系呢？说出你的判断和理由？ 在中心对称的两个图形中，连结对称点的线段都经过对称中心，并且被对称中心平分。如图，点O是正六边形ABCDEF的中心
（1）找出这个轴对称图形的对称轴．
（2）这个正六边形绕点O旋转多少
度后与原来的图形重合？
（3）如果换成其他的正多边形呢？
能得到一般的结论吗？ 答（1）直线AD、BE、CF、以及AB，BC，CD的垂直平分线都是这个正六边形的对称轴。（2）60°或其整数倍。（3）一般地，绕正n边形的中心旋转 或其整数倍都能与原来的图形重合。试一试思考题　　今有正方形的土地一块，要在其上修筑两条笔直的道路，使道路把这块土地分成形状相同且面积相等的四部分，若道路宽度可忽略不计，请你设计三种不同的修筑方案（在给出的图中的三个正方形上分别画图，并简述画图步骤.实验探究：如何画一条直线将下列图形分成面积相等的两部分。 规律：过两个中心对称图形的中心画出一条直线即可画一画移动一块正方形
（1）使得到图形只是轴对称图形；
（2）使得到图形只是中心对称图形；
（3）既是轴对称图形又是中心对称图形：讨论：中心对称与轴对称的区别：全课总结:中心对称与中心对称图形两个概念区别和联系
中心对称是 全等图形之间的 ；
中心对称图形是 图形本身成对称的 。中心对称的两个图形性质成中心对称的两个图形，对称点的连线都经过 ，并且被对称中心 。
成中心对称的两个图形是 ；全等形。对称中心平分画已知图形关于某点的中心对称图形关键是
作出各顶点的对称点。两个一个位置关系特性同学们，请不要停止探究的步伐，
　　　　数学源自于对生活的热心
……
感谢所有的同行！感谢同学们！　　　　教师感言