11.1同底数幂的乘法 学案

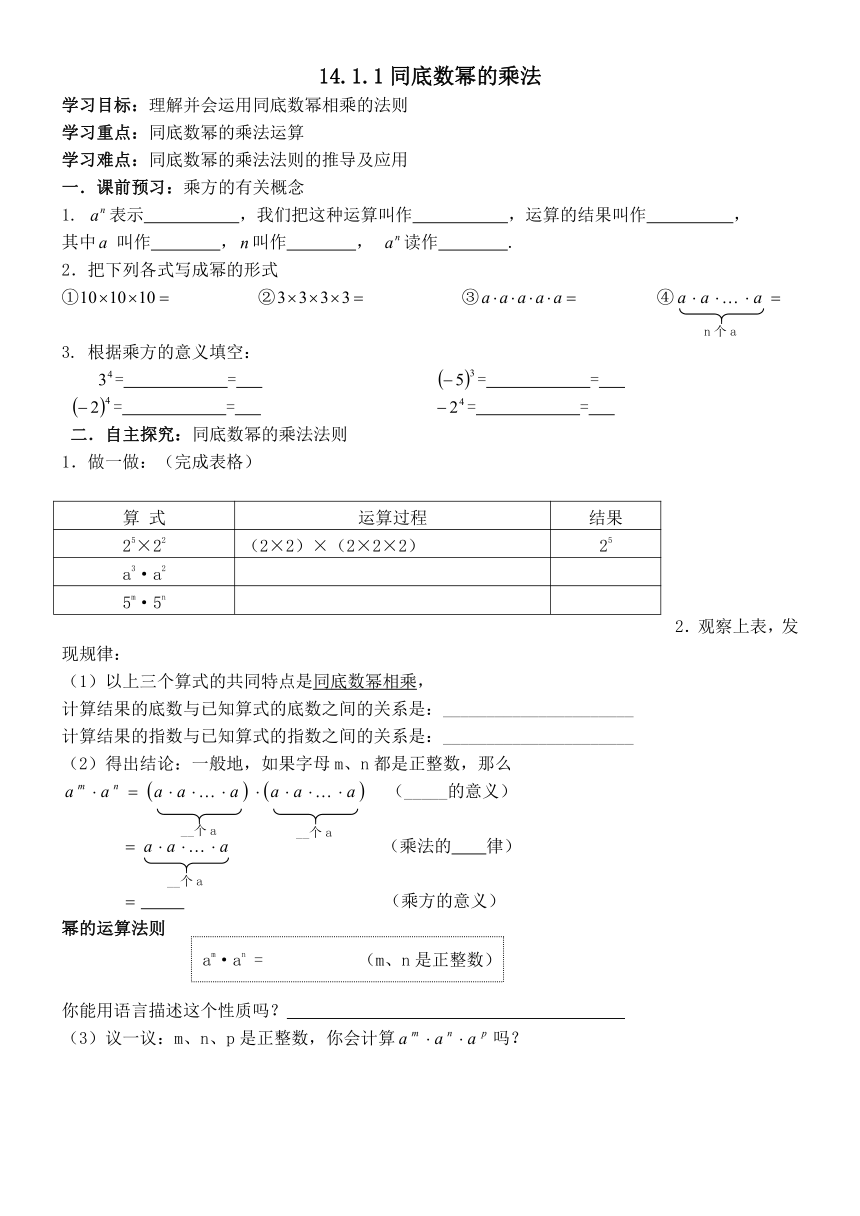
14.1.1同底数幂的乘法
学习目标：理解并会运用同底数幂相乘的法则
学习重点：同底数幂的乘法运算
学习难点：同底数幂的乘法法则的推导及应用
一．课前预习：乘方的有关概念
1. 表示 ，我们把这种运算叫作 ，运算的结果叫作 ，
其中叫作 ，叫作 ， 读作 .
2．把下列各式写成幂的形式
① ② ③ ④
3. 根据乘方的意义填空：
= = = =
= = = =
二．自主探究：同底数幂的乘法法则
1．做一做：（完成表格）
算 式 运算过程 结果
25×22 （2×2）×（2×2×2） 25
a3·a2
5m·5n
2．观察上表，发现规律：
（1）以上三个算式的共同特点是同底数幂相乘，
计算结果的底数与已知算式的底数之间的关系是：______________________
计算结果的指数与已知算式的指数之间的关系是：______________________
（2）得出结论：一般地，如果字母m、n都是正整数，那么
（_____的意义）
（乘法的 律）
（乘方的意义）
幂的运算法则
你能用语言描述这个性质吗？
（3）议一议：m、n、p是正整数，你会计算吗？
三、请大家自学例1例2，例3，看谁做得又对又快。
例1 计算.
① ②
例2.计算:
① ②
例3某台电脑每秒可作1015次运算，它工作5小时，可作多少次运算？
四、反思与提高
1、法则逆用，由am·an＝am+ ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )n（m、n都是正整数）得到am+n＝am·an＝am+1.an-1＝……根据需要而定。例xa＝4, xb＝7,求xa+b的值
(2)法则am·an＝am+n（m、n都是正整数）的使用范围
从例题1中看出，（1）（2）中看出底数都是一个数字，从例题2中看出（1）题中底数是字母。（2）中看出底数是一个多项式
看（x－y）3（x－y）5＝（x－y）8根据乘方的意义，把（x－y）看成整体
所以，同底数幂相乘时，底数可以是数字、字母、或多项式。
六、小结，这节课大家有什么收获？
达标测试
1、判断对错，对的在（ ）里打√，错的在（ ）里打×。
（1）a3+a4=a7( )(2)b5·b2=b7( ) (3)3m·2n=6m+n( )
（4）3m+2n=5m( ) (5)a2+a2=2a4( ) (6)5a3—a3=4a3( )
(7)m5·m6=m30 （ ） (8)a5·b6=(ab)11 ( )
（9）m + m3 =m4 ( ) （10）c·c3 =c3 ( )
2选择题
1.下列四个算式：①a6·a6=2a6；②m3+m2=m5；③x2·x·x8=x10；④y2+y2=y4．其中计算正确的有（ ）
A.0个 B.1个 C.2个 D.3个
2.m16可以写成（ ）
A.m8+m8 B.m8·m8 C.m2·m8 D.m4·m4
3.若xm=3，xn=5，则xm+n的值为（ ）
A.8 B.15 C.53 D.35
4.如果a2m-1·am+2=a7，则m的值是（ ）
A.2 B.3 C.4 D.5
3、若82a+2·8b-2=810,则2a+b= ,
4、计算
(1)x3·x2 (2)a4·a7·a (3)am+n·am (4)－32×34
（5）(a-b)3( a- b)2(a-b )
n个a
__个a
__个a
__个a
am·an = （m、n是正整数）