第五章 圆 5 确定圆的条件 第2课时 圆内接四边形 同步练习(含答案)
文档属性
| 名称 | 第五章 圆 5 确定圆的条件 第2课时 圆内接四边形 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 31.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 20:27:23 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 圆
5 确定圆的条件
第2课时 圆内接四边形
温馨提示
教材深挖:同学们,下面的结论可以在选择题或填空题中直接使用!
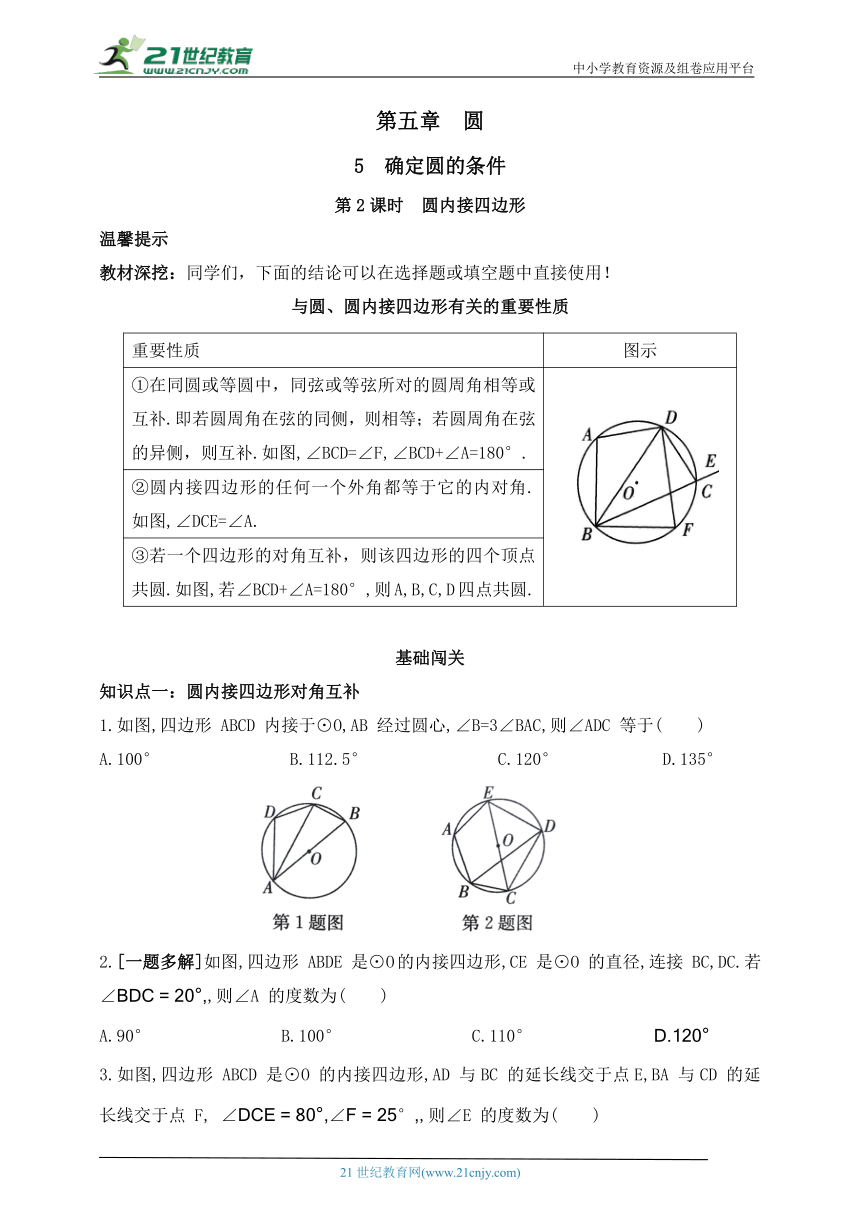
与圆、圆内接四边形有关的重要性质
重要性质 图示
①在同圆或等圆中,同弦或等弦所对的圆周角相等或互补.即若圆周角在弦的同侧,则相等;若圆周角在弦的异侧,则互补.如图,∠BCD=∠F,∠BCD+∠A=180°.
②圆内接四边形的任何一个外角都等于它的内对角.如图,∠DCE=∠A.
③若一个四边形的对角互补,则该四边形的四个顶点共圆.如图,若∠BCD+∠A=180°,则A,B,C,D四点共圆.
基础闯关
知识点一:圆内接四边形对角互补
1.如图,四边形 ABCD 内接于⊙O,AB 经过圆心,∠B=3∠BAC,则∠ADC 等于( )
A.100° B.112.5° C.120° D.135°
2.[一题多解]如图,四边形 ABDE 是⊙O的内接四边形,CE 是⊙O 的直径,连接 BC,DC.若 ,则∠A 的度数为( )
A.90° B.100° C.110°
3.如图,四边形 ABCD 是⊙O 的内接四边形,AD 与BC 的延长线交于点E,BA 与CD 的延长线交于点 F, ,则∠E 的度数为( )
C.45°
4.已知四边形 ABCD 内接于⊙O,且 则∠BCD的度数为____________.
知识点二:圆内接四边形的一个外角等于其内对角
5.[一题多辨](1)如图①,在⊙O中, 120°,点C 在 上,连接 AC,BC,过点 B 作
BD⊥AC 交AC 的延长线于点D,当点 C 从点 A 运动到点 B 的过程中,∠CBD 的度数( )
A.先增大后减小 B.先减小后增大 C.保持不变 D.一直减小
(2)如图②,四边形ABCD 是⊙O的内接四边形,AD =CD,点 E 在 AD 的延长线上, ∠CDE=52°,则∠AOD=____________ .
6.如图,四边形 ABCD 内接于⊙O,AI,CI 分别是∠BAC,∠BCA 的平分线, 点 E 在 AD 的延长线上,则∠CDE 的度数为( )
A.56° B.62° C.68° D.78°
能力提升
【构造圆内接四边形解决问题】
7.如图,点O 为线段BC的中点,点A,C,D到点O的距离相等,若
则 的度数是( )
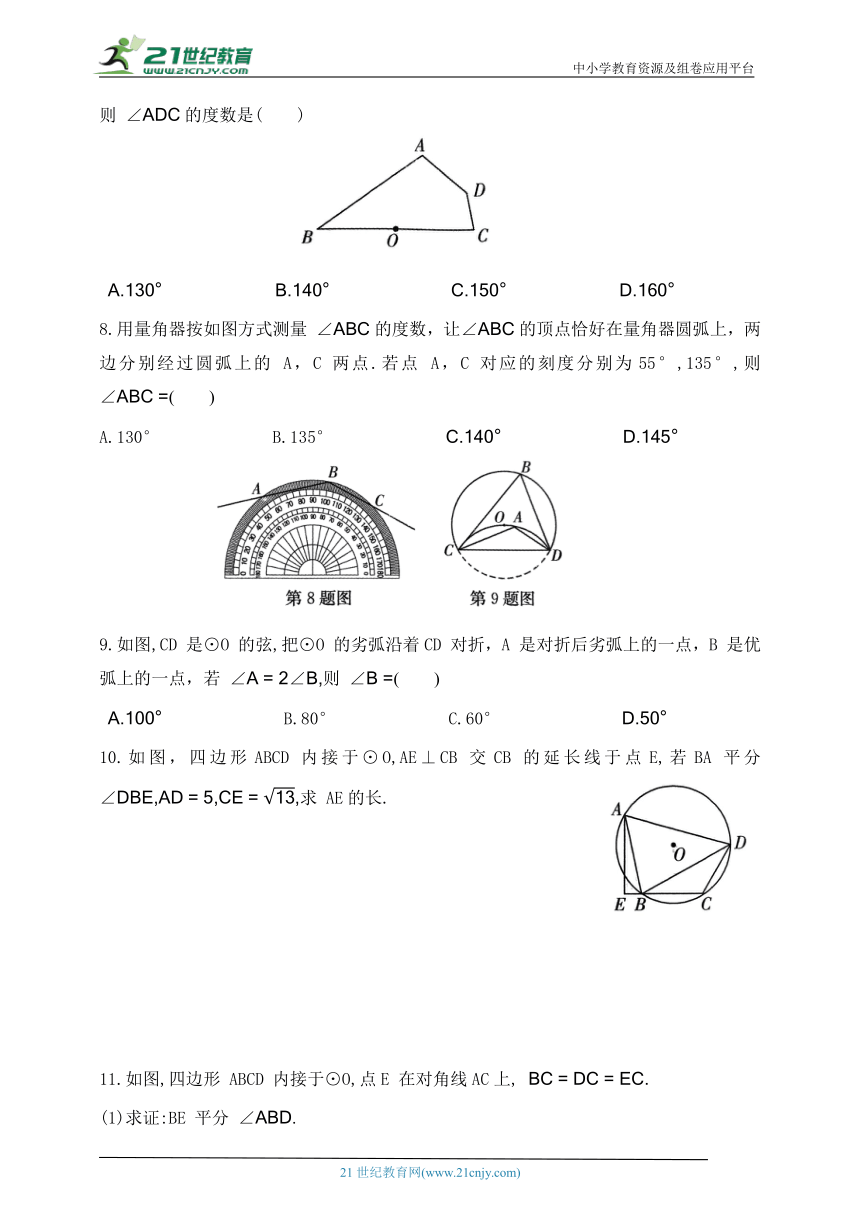
8.用量角器按如图方式测量 的度数,让的顶点恰好在量角器圆弧上,两边分别经过圆弧上的 A,C 两点.若点 A,C 对应的刻度分别为55°,135°,则 ( )
A.130° B.135°
9.如图,CD 是⊙O 的弦,把⊙O 的劣弧沿着CD 对折,A 是对折后劣弧上的一点,B 是优弧上的一点,若 则 ( )
B.80° C.60°
10.如图,四边形ABCD 内接于⊙O,AE⊥CB 交CB 的延长线于点E,若BA 平分 求 AE的长.
11.如图,四边形 ABCD 内接于⊙O,点E 在对角线AC上,
(1)求证:BE 平分 .
(2)若 求 的度数.
培优创新
12.已知⊙O 经过四边形ABCD 的B,D 两点,并与四条边分别交于点E,F,G,H,且
(1)如图①,连接 BD,若 BD是⊙O 的直径,求证:
(2)如图②,若 的度数为θ, 请写出θ,α和β之间的数量关系,并说明理由.
参考答案
1.B
2. C [解析]方法一:∵CE是⊙O的直径,∴∠CDE=90°.
∵∠BDC=20°,∴∠BDE=∠CDE-∠BDC=70°.
∵四边形 ABDE是⊙O的内接四边形,∴∠A=180°-∠BDE=110°.
方法二:连接OB,则∠BOC=40°,∴∠OCB=70°,∴∠A=110°.
3. C 4.70°或110°
5.(1)C
(2)52° [解析]∵四边形 ABCD 是⊙O的内接四边形,∴∠ABC+∠ADC=180°.
又∵∠CDE+∠ADC=180°,∴∠ABC=∠CDE=52°,∴∠AOC=2×52°=104°.
∵AD=CD,∴∠AOD=∠COD=104°÷2=52°.
6. C 7. B 8. C 9. C
10.解:如图,连接 AC.∵BA平分∠DBE,∴∠1=∠2.
∵∠1=∠CDA,∠2=∠3,∴∠3=∠CDA,∴AC=AD
11.(1)证明:∵BC=DC,∴∠CBD=∠CDB.∵∠CDB=∠BAC,∴∠CBD=∠BAC.
∵EC=BC,∴∠CEB =∠CBE.∵∠CEB=∠BAC+∠ABE,∠CBE=∠CBD+∠DBE,∴∠BAC +∠ABE =∠CBD+∠DBE,∴∠ABE=∠DBE,∴BE 平分∠ABD.
(2)解: ∵∠CBD=38°,∠CBD=∠BAC,∠CBD =∠CAD,
∴∠BAD=∠BAC+∠CAD=2∠CBD=2×38°=76°.
12.(1)证明:如图①,连接DF,DG.∵BD 是⊙O的直径,
∠HDG.
∵∠DFB=∠EDF+∠A,∠DGB=∠HDG+∠C,∴∠A=∠C.
(2)解:α+β+θ=180°.理由:如图
②,连接 DF,BH.
=180°,∴∠AFD=∠DHB.
∵∠A+∠ADF+∠AFD=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
5 确定圆的条件
第2课时 圆内接四边形
温馨提示
教材深挖:同学们,下面的结论可以在选择题或填空题中直接使用!
与圆、圆内接四边形有关的重要性质
重要性质 图示
①在同圆或等圆中,同弦或等弦所对的圆周角相等或互补.即若圆周角在弦的同侧,则相等;若圆周角在弦的异侧,则互补.如图,∠BCD=∠F,∠BCD+∠A=180°.
②圆内接四边形的任何一个外角都等于它的内对角.如图,∠DCE=∠A.
③若一个四边形的对角互补,则该四边形的四个顶点共圆.如图,若∠BCD+∠A=180°,则A,B,C,D四点共圆.
基础闯关
知识点一:圆内接四边形对角互补
1.如图,四边形 ABCD 内接于⊙O,AB 经过圆心,∠B=3∠BAC,则∠ADC 等于( )
A.100° B.112.5° C.120° D.135°
2.[一题多解]如图,四边形 ABDE 是⊙O的内接四边形,CE 是⊙O 的直径,连接 BC,DC.若 ,则∠A 的度数为( )
A.90° B.100° C.110°
3.如图,四边形 ABCD 是⊙O 的内接四边形,AD 与BC 的延长线交于点E,BA 与CD 的延长线交于点 F, ,则∠E 的度数为( )
C.45°
4.已知四边形 ABCD 内接于⊙O,且 则∠BCD的度数为____________.
知识点二:圆内接四边形的一个外角等于其内对角
5.[一题多辨](1)如图①,在⊙O中, 120°,点C 在 上,连接 AC,BC,过点 B 作
BD⊥AC 交AC 的延长线于点D,当点 C 从点 A 运动到点 B 的过程中,∠CBD 的度数( )
A.先增大后减小 B.先减小后增大 C.保持不变 D.一直减小
(2)如图②,四边形ABCD 是⊙O的内接四边形,AD =CD,点 E 在 AD 的延长线上, ∠CDE=52°,则∠AOD=____________ .
6.如图,四边形 ABCD 内接于⊙O,AI,CI 分别是∠BAC,∠BCA 的平分线, 点 E 在 AD 的延长线上,则∠CDE 的度数为( )
A.56° B.62° C.68° D.78°
能力提升
【构造圆内接四边形解决问题】
7.如图,点O 为线段BC的中点,点A,C,D到点O的距离相等,若
则 的度数是( )
8.用量角器按如图方式测量 的度数,让的顶点恰好在量角器圆弧上,两边分别经过圆弧上的 A,C 两点.若点 A,C 对应的刻度分别为55°,135°,则 ( )
A.130° B.135°
9.如图,CD 是⊙O 的弦,把⊙O 的劣弧沿着CD 对折,A 是对折后劣弧上的一点,B 是优弧上的一点,若 则 ( )
B.80° C.60°
10.如图,四边形ABCD 内接于⊙O,AE⊥CB 交CB 的延长线于点E,若BA 平分 求 AE的长.
11.如图,四边形 ABCD 内接于⊙O,点E 在对角线AC上,
(1)求证:BE 平分 .
(2)若 求 的度数.
培优创新
12.已知⊙O 经过四边形ABCD 的B,D 两点,并与四条边分别交于点E,F,G,H,且
(1)如图①,连接 BD,若 BD是⊙O 的直径,求证:
(2)如图②,若 的度数为θ, 请写出θ,α和β之间的数量关系,并说明理由.
参考答案
1.B
2. C [解析]方法一:∵CE是⊙O的直径,∴∠CDE=90°.
∵∠BDC=20°,∴∠BDE=∠CDE-∠BDC=70°.
∵四边形 ABDE是⊙O的内接四边形,∴∠A=180°-∠BDE=110°.
方法二:连接OB,则∠BOC=40°,∴∠OCB=70°,∴∠A=110°.
3. C 4.70°或110°
5.(1)C
(2)52° [解析]∵四边形 ABCD 是⊙O的内接四边形,∴∠ABC+∠ADC=180°.
又∵∠CDE+∠ADC=180°,∴∠ABC=∠CDE=52°,∴∠AOC=2×52°=104°.
∵AD=CD,∴∠AOD=∠COD=104°÷2=52°.
6. C 7. B 8. C 9. C
10.解:如图,连接 AC.∵BA平分∠DBE,∴∠1=∠2.
∵∠1=∠CDA,∠2=∠3,∴∠3=∠CDA,∴AC=AD
11.(1)证明:∵BC=DC,∴∠CBD=∠CDB.∵∠CDB=∠BAC,∴∠CBD=∠BAC.
∵EC=BC,∴∠CEB =∠CBE.∵∠CEB=∠BAC+∠ABE,∠CBE=∠CBD+∠DBE,∴∠BAC +∠ABE =∠CBD+∠DBE,∴∠ABE=∠DBE,∴BE 平分∠ABD.
(2)解: ∵∠CBD=38°,∠CBD=∠BAC,∠CBD =∠CAD,
∴∠BAD=∠BAC+∠CAD=2∠CBD=2×38°=76°.
12.(1)证明:如图①,连接DF,DG.∵BD 是⊙O的直径,
∠HDG.
∵∠DFB=∠EDF+∠A,∠DGB=∠HDG+∠C,∴∠A=∠C.
(2)解:α+β+θ=180°.理由:如图
②,连接 DF,BH.
=180°,∴∠AFD=∠DHB.
∵∠A+∠ADF+∠AFD=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
