苏科版八年级数学上册2.5等腰三角形的轴对称性 课件(共37张PPT)
文档属性
| 名称 | 苏科版八年级数学上册2.5等腰三角形的轴对称性 课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 08:42:13 | ||
图片预览







文档简介
(共37张PPT)
2.5等腰三角形的轴对称性(1)
你知道什么样的三角形是等腰三角形吗
有两边相等的三角形叫等腰三角形.
你能找出下页图片的哪些物体
有等腰三角形的形状吗?
按下面的步骤做一做
1
、将长方形纸片对折.
2
、然后沿虚线折叠,再沿折痕剪开.
3
、把阴影部分展开,得到的三角形有什么特点?
A
B
C
D
你有什么发现
A
B
C
A
D
C
A
B
C
D
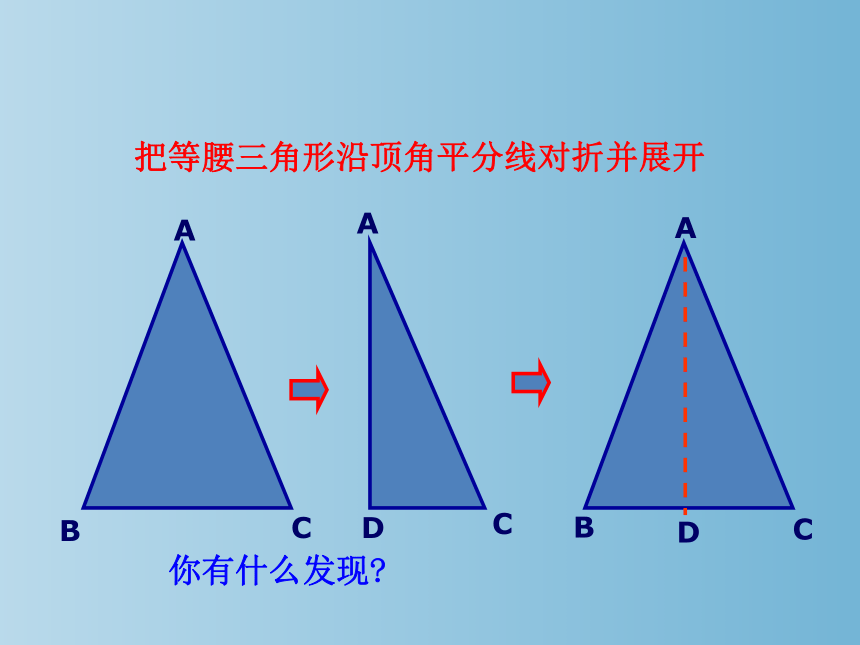
把等腰三角形沿顶角平分线对折并展开
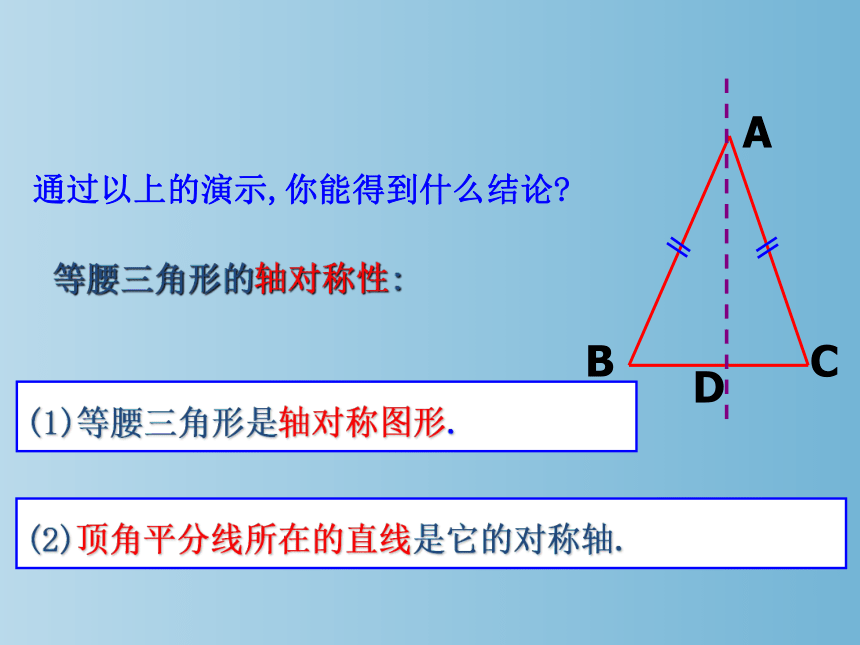
(1)等腰三角形是轴对称图形.
(2)顶角平分线所在的直线是它的对称轴.
等腰三角形的轴对称性:
A
C
B
D
通过以上的演示,你能得到什么结论
AB=AC
BD=CD
∠BAD=∠CAD
∠B=∠C
∠ADB=∠ADC
B
A
C
D
把剪出的等腰三角形沿折痕对折,
找出其中重合的线段和角.
重合的线段:
重合的角:
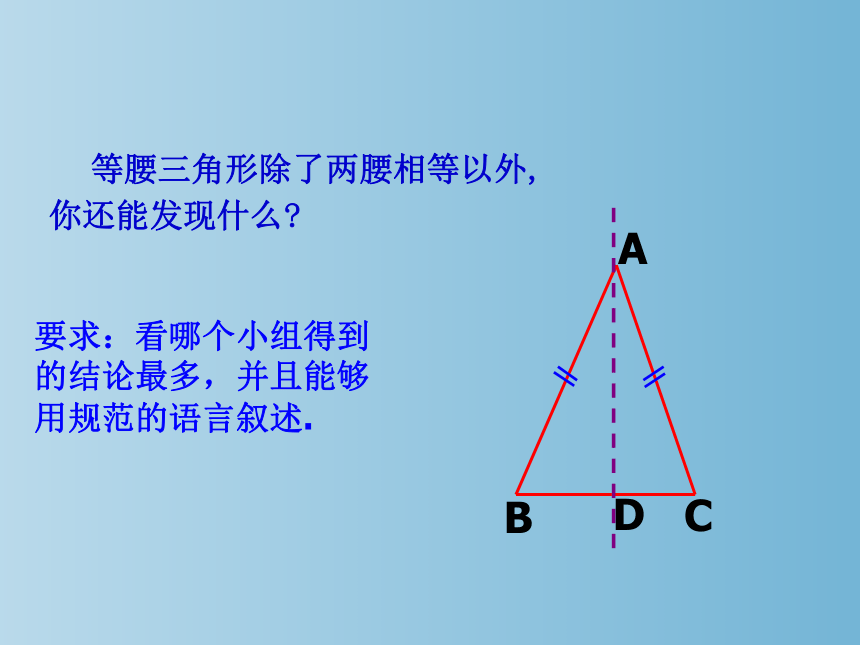
等腰三角形除了两腰相等以外,
你还能发现什么
要求:看哪个小组得到的结论最多,并且能够用规范的语言叙述.
A
B
C
D
A
C
B
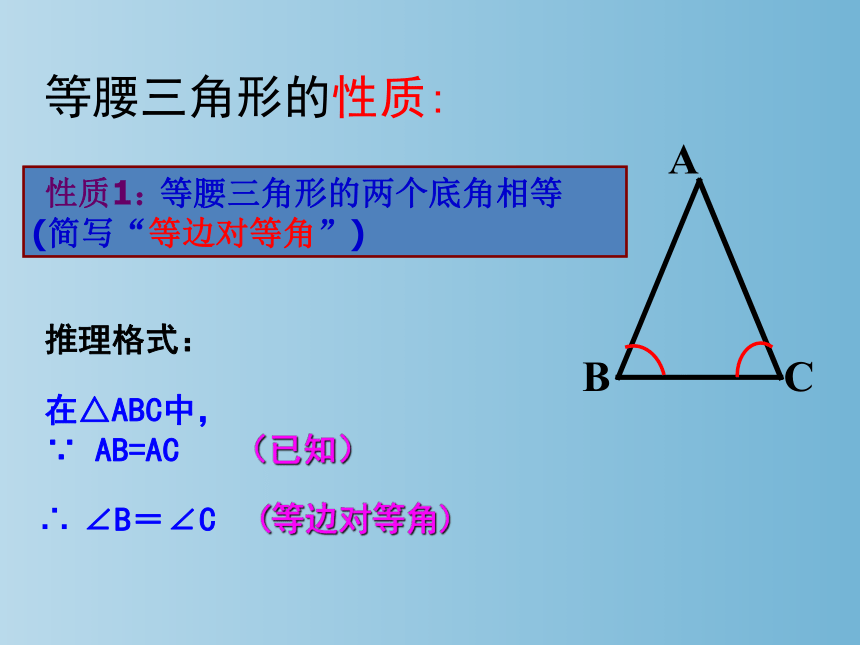
等腰三角形的性质:
等腰三角形的两个底角相等 (简写“等边对等角”)
在△ABC中,
∵ AB=AC
∴ ∠B=∠C
(等边对等角)
推理格式:
性质1:
(已知)
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
┓
顶角的平分线
底边上的高
底边上的中线
A
B
C
D
A
B
C
D
┓
A
B
C
D
A
B
C
D
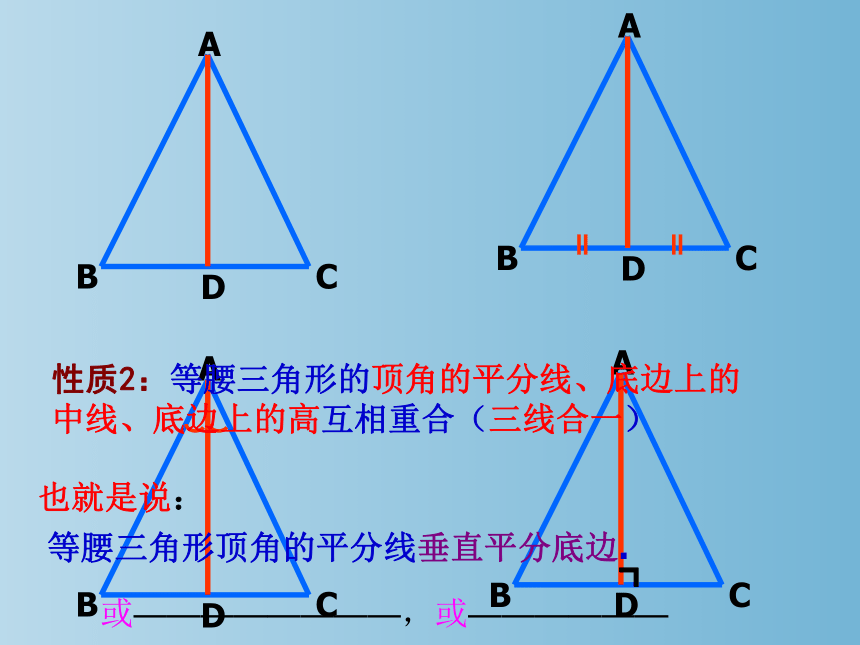
性质2:等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合(三线合一)
也就是说:
等腰三角形顶角的平分线垂直平分底边.
或————————,或——————
在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____.
C
A
B
1
2
D
等腰三角形“三线合一”的性质
用符号语言表示为:
1
2
BD
CD
1
2
AD
BC
AD
BC
BD
CD
等腰三角形“三线合一”的性质
评注:在做题过程中,若想使用三线合一,题中至少要出现三线中的一线,即“一线生机”.
(1)如果等腰三角形的一个底角为500,则其余两个角为____和____.
(2)如果等腰三角形的顶角为800,则它的一个底角为____.
500
800
500
(3)如果等腰三角形的一个角为800,则其余两个角为___________________.
800 和200
(4)如果等腰三角形的一个角为1000,则其余两个角为_________.
400和400
或500和500
(5)等腰三角形的一个外角为1300,则三个内角分别:_______________________________.
650、650、500
或500、500、800
知识应用:
点评:
等腰三角形中的内角,若没指出是底
角还是顶角应分两种情况讨论,注意
运用三角形内角之和等于180 °.
等腰三角形的性质
文字叙述
几何语言
等腰三角形的两底角相等(简称“等边对等角”)
∵AB=AC
∴∠B=∠C
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合,简称“三线合一”
∵AB=AC,∠1=∠2 ∴AD⊥BC,BD=CD
小结
2.5等腰三角形的轴对称性(2)
1.等腰三角形有哪些性质?
2.在一个三角形中,如果有两个角相等,那么这两个角所对的边的大小有什么关系?
请同学们分别拿出一张半透明纸,做一个实验,按以下方法进行操作:
1.在半透明纸上画一条长为6cm的线段BC.
2.以BC为始边,分别以点B和点C为顶点,用量角器画两个相等的锐角,两角终边的交点为A.
3.找出BC的中点D,连接AD,然后沿AD对折.
问题1:AB与AC是否重合?
问题2:本实验的条件与结论
如何用文字语言加以叙述?
B
C
A
D
.
在△BAT和△CAT中,
∠1=∠2(角平分线定义),
∠B=∠C(已知),
AT=AT(公共边) ,
∴△BAT≌△CAT(AAS),
∴AB=AC(全等三角形对应边相等).
已知:在△ABC中,∠B=∠C
求证:AB=AC.
证明:(1)作∠A的平分线交BC于T.
A
B
C
T
(2)过A点作AD⊥BC,垂足为D.
A
B
C
D
∵AD⊥BC,
∴∠ADB=∠ADC,
在△ADB和△ADC中,
∠ADB=∠ADC,
∠B=∠C,
AD=AD,
∴△ADB≌△ADC,
∴AB=AC.
思考:通过这题的证明你发现了什么结论?
1
2
定理 有两个角相等的三角形是等腰三角形.(简称“等角对等边”).
符号语言
∵∠B=∠C
∴AB=AC (等角对等边)
思考:
“等边对等角”与“等角对等边”
是否一样?它们的主要区别在哪里?
已知:如图,在△ABC中,∠B=∠C.求证:AB=AC.
证明:作AD⊥BC于点D,
则∠ADB=∠ADC=90°.
在△ABD和△ACD中,
∴△ABD≌△ACD(AAS).∴AB=AC.
如图,DB=DC,∠ABD=∠ACD.求证:AB=AC.
∴AB=AC.
证明:连接BC,如图.
∵DB=DC,∴∠DBC=∠DCB.
又∵∠ABD=∠ACD,
∴∠DBC+∠ABD=∠DCB+∠ACD,
即∠ABC=∠ACB.
思考1:什么是等边三角形?
它与等腰三角形有什么区别与联系?
思考2:等边三角形的性质有哪些?
等腰三角形 等边三角形
对称性 轴对称图形(1条)
边 两腰相等
角 两底角相等
特殊线 三线合一(1条)
轴对称图形(3条)
三边相等
三个角都等于60度
三线合一(3条)
等边三角形的概念及性质
(1)三边相等的三角形叫作等边三角形或正三角形.
(2)等边三角形是轴对称图形,并且有3条对称轴.
(3)等边三角形的各角都等于60°.
【小结】
思考3:一个三角形满足什么条件就是等边三角形?为什么?
等边三角形的判定
(1)三个角都相等的三角形是等边三角形.
(2)有一个角是60°的等腰三角形是等边三角形 .
【小结】
【小结 】
等腰三角形 等边三角形
对称性 轴对称图形(1条)
边 两腰相等
角 两底角相等
特殊线 三线合一(1条)
轴对称图形(3条)
三边相等
三个角都等于60度
三线合一(3条)
等边三角形的判定
(1)三个角都相等的三角形是等边三角形.
(2)有一个角是60°的等腰三角形是等边三角形 .
2.5等腰三角形的轴对称性(3)
你能用折纸的方法将一个直角三角形分成两个等腰三角形吗?
1.任意剪出一张直角三角形纸片(如图1).
2.剪得的纸片是否能折成图2的形状?
3.△ACD与△BCD为什么是等腰三角形?请说明理由.
图1
图2
图3
你还有其他发现吗?
定理 直角三角形斜边上的中线等于斜边的一半.
符号语言:
∵在Rt△ABC中,点D是AB的中点,
∴CD= AB .
【例】
如图,∠ACB=∠ADB=90°,N、M分别是AB、CD的中点,探究MN与CD的位置关系
如图,连接DN、CN.
∵在△ADB中,∠ADB=90°,N是AB的中点,∴DN=AB.
同理可得,CN=AB.
∴DN=CN.
在△DNC中,∵DN=CN,M是CD的中点,
∴MN⊥CD,即MN垂直平分CD.
探究:如图,Rt△ABC,∠ACB=90°,如果
∠A=30°,那么BC与AB有怎样的数量关系?
试证明你的结论.
解:BC= AB.
.
直角三角形中,30°的角所对的直角边等于斜边的一半。
证明:作斜边上的中线CD,
∵∠ACB=90°,∠A=30°,
∴∠B=60°.
∵∠ACB=90°,CD是斜边上的中线,
∴
∴△BCD是等边三角形(有一个角是60°的等腰三角形是等边三角形).
∴ .
(直角三角形斜边上的中线等于斜边的一半).
【小结】
定理 直角三角形斜边上的中线等于斜边的一半.
直角三角形中,30°的角所对的直角边等于斜边的一半。
谢 谢 观 看
2.5等腰三角形的轴对称性(1)
你知道什么样的三角形是等腰三角形吗
有两边相等的三角形叫等腰三角形.
你能找出下页图片的哪些物体
有等腰三角形的形状吗?
按下面的步骤做一做
1
、将长方形纸片对折.
2
、然后沿虚线折叠,再沿折痕剪开.
3
、把阴影部分展开,得到的三角形有什么特点?
A
B
C
D
你有什么发现
A
B
C
A
D
C
A
B
C
D
把等腰三角形沿顶角平分线对折并展开
(1)等腰三角形是轴对称图形.
(2)顶角平分线所在的直线是它的对称轴.
等腰三角形的轴对称性:
A
C
B
D
通过以上的演示,你能得到什么结论
AB=AC
BD=CD
∠BAD=∠CAD
∠B=∠C
∠ADB=∠ADC
B
A
C
D
把剪出的等腰三角形沿折痕对折,
找出其中重合的线段和角.
重合的线段:
重合的角:
等腰三角形除了两腰相等以外,
你还能发现什么
要求:看哪个小组得到的结论最多,并且能够用规范的语言叙述.
A
B
C
D
A
C
B
等腰三角形的性质:
等腰三角形的两个底角相等 (简写“等边对等角”)
在△ABC中,
∵ AB=AC
∴ ∠B=∠C
(等边对等角)
推理格式:
性质1:
(已知)
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
┓
顶角的平分线
底边上的高
底边上的中线
A
B
C
D
A
B
C
D
┓
A
B
C
D
A
B
C
D
性质2:等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合(三线合一)
也就是说:
等腰三角形顶角的平分线垂直平分底边.
或————————,或——————
在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____.
C
A
B
1
2
D
等腰三角形“三线合一”的性质
用符号语言表示为:
1
2
BD
CD
1
2
AD
BC
AD
BC
BD
CD
等腰三角形“三线合一”的性质
评注:在做题过程中,若想使用三线合一,题中至少要出现三线中的一线,即“一线生机”.
(1)如果等腰三角形的一个底角为500,则其余两个角为____和____.
(2)如果等腰三角形的顶角为800,则它的一个底角为____.
500
800
500
(3)如果等腰三角形的一个角为800,则其余两个角为___________________.
800 和200
(4)如果等腰三角形的一个角为1000,则其余两个角为_________.
400和400
或500和500
(5)等腰三角形的一个外角为1300,则三个内角分别:_______________________________.
650、650、500
或500、500、800
知识应用:
点评:
等腰三角形中的内角,若没指出是底
角还是顶角应分两种情况讨论,注意
运用三角形内角之和等于180 °.
等腰三角形的性质
文字叙述
几何语言
等腰三角形的两底角相等(简称“等边对等角”)
∵AB=AC
∴∠B=∠C
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合,简称“三线合一”
∵AB=AC,∠1=∠2 ∴AD⊥BC,BD=CD
小结
2.5等腰三角形的轴对称性(2)
1.等腰三角形有哪些性质?
2.在一个三角形中,如果有两个角相等,那么这两个角所对的边的大小有什么关系?
请同学们分别拿出一张半透明纸,做一个实验,按以下方法进行操作:
1.在半透明纸上画一条长为6cm的线段BC.
2.以BC为始边,分别以点B和点C为顶点,用量角器画两个相等的锐角,两角终边的交点为A.
3.找出BC的中点D,连接AD,然后沿AD对折.
问题1:AB与AC是否重合?
问题2:本实验的条件与结论
如何用文字语言加以叙述?
B
C
A
D
.
在△BAT和△CAT中,
∠1=∠2(角平分线定义),
∠B=∠C(已知),
AT=AT(公共边) ,
∴△BAT≌△CAT(AAS),
∴AB=AC(全等三角形对应边相等).
已知:在△ABC中,∠B=∠C
求证:AB=AC.
证明:(1)作∠A的平分线交BC于T.
A
B
C
T
(2)过A点作AD⊥BC,垂足为D.
A
B
C
D
∵AD⊥BC,
∴∠ADB=∠ADC,
在△ADB和△ADC中,
∠ADB=∠ADC,
∠B=∠C,
AD=AD,
∴△ADB≌△ADC,
∴AB=AC.
思考:通过这题的证明你发现了什么结论?
1
2
定理 有两个角相等的三角形是等腰三角形.(简称“等角对等边”).
符号语言
∵∠B=∠C
∴AB=AC (等角对等边)
思考:
“等边对等角”与“等角对等边”
是否一样?它们的主要区别在哪里?
已知:如图,在△ABC中,∠B=∠C.求证:AB=AC.
证明:作AD⊥BC于点D,
则∠ADB=∠ADC=90°.
在△ABD和△ACD中,
∴△ABD≌△ACD(AAS).∴AB=AC.
如图,DB=DC,∠ABD=∠ACD.求证:AB=AC.
∴AB=AC.
证明:连接BC,如图.
∵DB=DC,∴∠DBC=∠DCB.
又∵∠ABD=∠ACD,
∴∠DBC+∠ABD=∠DCB+∠ACD,
即∠ABC=∠ACB.
思考1:什么是等边三角形?
它与等腰三角形有什么区别与联系?
思考2:等边三角形的性质有哪些?
等腰三角形 等边三角形
对称性 轴对称图形(1条)
边 两腰相等
角 两底角相等
特殊线 三线合一(1条)
轴对称图形(3条)
三边相等
三个角都等于60度
三线合一(3条)
等边三角形的概念及性质
(1)三边相等的三角形叫作等边三角形或正三角形.
(2)等边三角形是轴对称图形,并且有3条对称轴.
(3)等边三角形的各角都等于60°.
【小结】
思考3:一个三角形满足什么条件就是等边三角形?为什么?
等边三角形的判定
(1)三个角都相等的三角形是等边三角形.
(2)有一个角是60°的等腰三角形是等边三角形 .
【小结】
【小结 】
等腰三角形 等边三角形
对称性 轴对称图形(1条)
边 两腰相等
角 两底角相等
特殊线 三线合一(1条)
轴对称图形(3条)
三边相等
三个角都等于60度
三线合一(3条)
等边三角形的判定
(1)三个角都相等的三角形是等边三角形.
(2)有一个角是60°的等腰三角形是等边三角形 .
2.5等腰三角形的轴对称性(3)
你能用折纸的方法将一个直角三角形分成两个等腰三角形吗?
1.任意剪出一张直角三角形纸片(如图1).
2.剪得的纸片是否能折成图2的形状?
3.△ACD与△BCD为什么是等腰三角形?请说明理由.
图1
图2
图3
你还有其他发现吗?
定理 直角三角形斜边上的中线等于斜边的一半.
符号语言:
∵在Rt△ABC中,点D是AB的中点,
∴CD= AB .
【例】
如图,∠ACB=∠ADB=90°,N、M分别是AB、CD的中点,探究MN与CD的位置关系
如图,连接DN、CN.
∵在△ADB中,∠ADB=90°,N是AB的中点,∴DN=AB.
同理可得,CN=AB.
∴DN=CN.
在△DNC中,∵DN=CN,M是CD的中点,
∴MN⊥CD,即MN垂直平分CD.
探究:如图,Rt△ABC,∠ACB=90°,如果
∠A=30°,那么BC与AB有怎样的数量关系?
试证明你的结论.
解:BC= AB.
.
直角三角形中,30°的角所对的直角边等于斜边的一半。
证明:作斜边上的中线CD,
∵∠ACB=90°,∠A=30°,
∴∠B=60°.
∵∠ACB=90°,CD是斜边上的中线,
∴
∴△BCD是等边三角形(有一个角是60°的等腰三角形是等边三角形).
∴ .
(直角三角形斜边上的中线等于斜边的一半).
【小结】
定理 直角三角形斜边上的中线等于斜边的一半.
直角三角形中,30°的角所对的直角边等于斜边的一半。
谢 谢 观 看
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
