初中数学人教版九年级上册 25.3.2用频率估计概率解决问题 课件 (共27张PPT)
文档属性
| 名称 | 初中数学人教版九年级上册 25.3.2用频率估计概率解决问题 课件 (共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 975.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
25.3.2用频率估计概率解决问题
人教版九年级上册
教学目标
1.会用频率估计概率并解决实际问题.
2.通过对树苗移植成活率、柑橘损坏率问题的探究,培养根据频率的稳定趋势估计概率的能力,感受概率在问题决策中的重要作用,提升统计的意识,培养应用数学的意识
新知导入
对一般的随机事件,在做大量的重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性.
因此,可以通过大量的重复试验,用一个随机事件发生的频率估计它的概率.
新知讲解
幼苗移植会有哪些可能结果?
概率
成活
不成活
两种结果可能性是否相等未知
利用频率估计概率
不能用列举法
某林业部门要考察某种幼树在一定条件下的移植成活率,应采用什么具体做法?
新知讲解
如何利用频率去估计幼树移植的成活率呢?
在相同条件下,对这种幼树进行大量移植,并统计成活数m的情况,计算成活的频率.随着移植数n越来越大,频率会越来越稳定,于是就可以把频率作为成活率的估计值.
实际上有的实验做起来非常麻烦,并且大量的进行这个实验也是不可能的,这就需要“模拟实验”来代替.
新知讲解
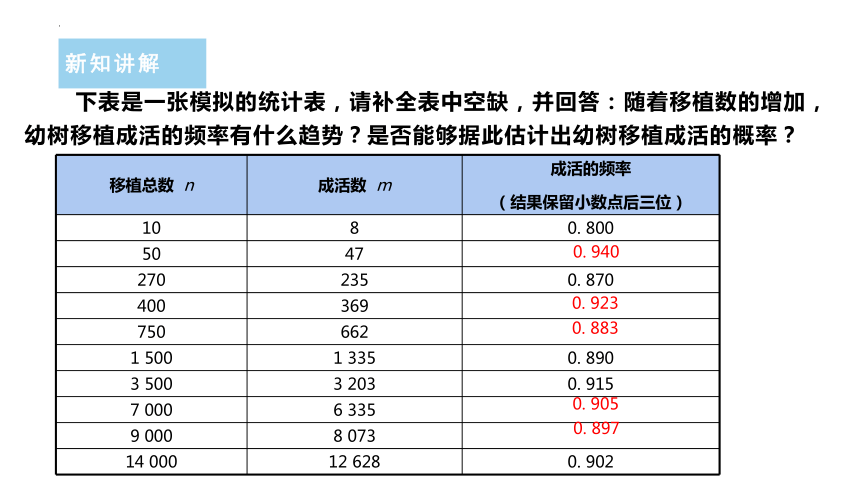
下表是一张模拟的统计表,请补全表中空缺,并回答:随着移植数的增加,幼树移植成活的频率有什么趋势?是否能够据此估计出幼树移植成活的概率?
移植总数 n 成活数 m 成活的频率
(结果保留小数点后三位)
10 8 0. 800
50 47
270 235 0. 870
400 369
750 662
1 500 1 335 0. 890
3 500 3 203 0. 915
7 000 6 335
9 000 8 073
14 000 12 628 0. 902
0. 940
0. 923
0. 883
0. 905
0. 897
新知讲解
从表中可以发现,随着移植数的增加,幼树移植成活的频率越来越稳定.当移植总数为14000时,成活的频率为0.902,于是可以估计幼树移植成活的概率为____.
0.9
归纳总结
一般可以用试验次数累计最多时的频率作为概率的估计值.概率估计值小数点后保留的位数不超过频率小数点后保留的位数.
注意
典例精析
某水果公司以2元/kg的成本价新进10 000kg柑橘.如果公司希望这些柑橘能够获得利润5000元,那么在出售柑橘(去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
1、出售柑橘(去掉损坏的柑橘)定价时需要注意哪些问题?
柑橘在运输、储存中会有损坏,公司必须估算出可能损坏的柑橘总数,以便将损坏的柑橘的成本折算到没有损坏的柑橘的售价中,才能保证实际获得的利润.
典例精析
请补全表中空缺,并完成填空(结果保留三位小数):
柑橘总质量 n / 千克 损坏柑橘质量 m / 千克 柑橘损坏的频率(m/n)
50 5.50 0.110
100 10.50 0.105
150 15.15
200 19.42
250 24.25
300 30.93
350 35.32
400 39.24
450 44.57
500 51.54
0.101
0.097
0.097
0.103
0.101
0.098
0.099
0.103
典例精析
若柑橘没有损坏,要获得 5 000 元利润应如何定价?
柑橘损坏后,柑橘的重量减少了,为了确保获得5 000 元利润,定价应如何变化?如何知道柑橘的重量将减少多少?
随着统计的频率越来越稳定,柑橘的损坏率为 0.1,
则柑橘的完好概率为 0.9.
设每千克柑橘的售价为x 元,
根据“利润=(售价-实际成本) 完好的质量”列方程求解.
典例精析
解:销售人员已经对柑橘损坏率进行了抽样统计,填完表格后可以看出,随着柑橘质量的增加,柑橘损坏的频率越来越稳定.柑橘总质量为 500 kg 时的损坏频率为 0.103,于是可以估计柑橘损坏的概率约为 0.1(结果保留小数点后一位).由此可知,柑橘完好的概率为0.9.
典例精析
根据估计的概率可以知道,在10000kg柑橘中完好柑橘的质量为
10000×0.9=9000(kg)
完好柑橘的实际成本为
= ≈2.22(元/kg)
设每千克柑橘的售价为x元,则
(x-2.22)×9000=5000,解得 x≈2.8
因此,出售柑橘时,每千克定价大约2.8元可获利润5000元.
归纳总结
在大量的重复试验中,随机事件发生的频率会呈现出明显的规律性:随着试验次数的增加,频率将会越来越集中在一个常数附近,具有稳定性.概率是频率的稳定值,而频率是概率的近似值.
课堂练习
【知识技能类作业】必做题:
1. 某林业局将一种树苗移植成活的情况绘制成如下统计图,由此可估计这种树苗移植成活的概率约为( )
A. 0.95 B. 0.90 C. 0.85 D. 0.80
2.一个暗箱里放有a个除颜色外完全相同的球,这a个球中红球只有4个,若每次将球搅匀后,任意摸出1个球记下颜色再放回暗箱,通过大量重复摸球实验后发现,摸到红球的频率稳定在20%附近,那么可以推算出a大约是( )
A.25 B.20 C.15 D.10
B
B
课堂练习
【知识技能类作业】必做题:
3.在围棋盒中有x颗白色棋子和y颗黑色棋子,从盒中随机取出一颗棋子,取得白色棋子的概率是.如果再往盒中放进12颗白色棋子,取得白色棋子的概率是,则原来盒中有白色棋子有_____颗.
4.为了估计鱼塘中鱼的条数,养鱼者首先从鱼塘中打捞30条鱼做上标记,然后放归鱼塘,经过一段时间,等有标记的鱼完全混合于鱼群中,再打捞200条鱼,发现其中带标记的鱼有5条,则鱼塘中估计有_______条鱼.
4
1200
课堂练习
【知识技能类作业】选做题:
5.为了比较甲、乙两鱼池中的鱼苗数目,小明从两鱼池中各捞出100条鱼苗,每条做好记号,然后放回原鱼池;一段时间后,在同样的地方,小明再从甲、乙两鱼池中各捞出100条鱼苗,发现其中有记号的鱼苗分别是5条、10条,可以初步估计鱼苗数目较多的是哪个鱼池
课堂练习
【知识技能类作业】选做题:
解:设甲鱼池鱼的总数为x条,则
鱼的概率近似,解得x=2000;
设乙鱼池鱼的总数为y条,则
鱼的概率近似,解得y=1000;
,
可以初步估计鱼苗数目较多的是甲鱼池
课堂练习
【综合拓展类作业】
6.“网红”长沙入选2021年“五一”假期热门旅游城市.本市某景点为吸引游客,设置了一种游戏,其规则如下:凡参与游戏的游客从一个装有12个红球和若干个白球(每个球除颜色外,其他都相同)的不透明纸箱中,随机摸出一个球,摸到红球就可免费得到一个景点吉祥物.据统计参与这种游戏的游客共有60000人,景点一共为参与该游戏的游客免费发放了景点吉祥物15000个.
(1)求参与该游戏可免费得到景点吉祥物的频率;
(2)请你估计纸箱中白球的数量接近多少?
课堂练习
【综合拓展类作业】
解:(1)由题意得:15000÷60000=0.25 ,
答:参与该游戏可免费得到景点吉祥物的频率为0.25 ;
(2)设纸箱中白球的数量为 x个,
由(1)可知,随机摸出一个球是红球的概率约为0.25 ,
则 ,
解得x=36 ,
经检验, x=36是所列分式方程的解,且符合题意,
答:纸箱中白球的数量接近36个.
课堂总结
注意:
用频率估计概率:
在相同条件下,做大量重复试验,事件发生的频率会越来越稳定,我们可以把频率作为概率的估计值.
一般可以用试验次数累计最多时的频率作为概率的估计值.概率估计值小数点后保留的位数不超过频率小数点后保留的位数.
用
频
率
估
计
概
率
板书设计
用频率估计概率:
在相同条件下,做大量重复试验,事件发生的频率会越来越稳定,我们可以把频率作为概率的估计值
作业布置
【知识技能类作业】必做题:
1.一个不透明的袋子中装有2个红球和若干个黄球,这些球除颜色外都相同.经过多次试验发现,摸出红球的频率稳定在 左右,则袋子中的黄球个数最有可能是( )
A.1 B.2 C.4 D.6
2.在一个不透明的袋中装有若干个红球和4个黑球,每个球除颜色外完全相同.摇匀后从中摸出一个球,记下颜色后再放回袋中.不断重复这一过程,共摸球100次.其中有40次摸到黑球,估计袋中红球的个数是 .
B
6
作业布置
【知识技能类作业】选做题:
3.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同,小刚通过多次摸球试验后发现其中摸到红色,黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是 个.
4.某鱼塘里养了1600 条鲤鱼、若干条草鱼和 800条罗非鱼,该鱼塘主通过多次捕捞试验后发现,捕捞到草鱼的频率稳定在 0.5左右,若该鱼塘主随机在鱼塘捕捞一条鱼,则捞到鲤鱼的概率约为 .
24
作业布置
【综合拓展类作业】
5.小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,他在封闭图形内划出了一个半径为1米的圆,在不远处向图形内掷石子,且记录如下:
作业布置
【综合拓展类作业】
(1)随着次数的增多,小明发现m与n的比值在一个常数k附近波动,请你写出k的值.
(2)请利用学过的知识求出封闭图形ABC的大致面积.
作业布置
【综合拓展类作业】
(1)根据统计表,可得石子落在圆内的概率与落在阴影部分的概率之比k= = ;
(2)石子落在圆内和石子落在阴影内的次数关系,随着试验次数的增多,逐渐趋向于为1:2,
所以圆的面积约占封闭图形ABC面积的 ,
因为S圆=π,
所以封闭图形ABC的面积约为3π.
25.3.2用频率估计概率解决问题
人教版九年级上册
教学目标
1.会用频率估计概率并解决实际问题.
2.通过对树苗移植成活率、柑橘损坏率问题的探究,培养根据频率的稳定趋势估计概率的能力,感受概率在问题决策中的重要作用,提升统计的意识,培养应用数学的意识
新知导入
对一般的随机事件,在做大量的重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性.
因此,可以通过大量的重复试验,用一个随机事件发生的频率估计它的概率.
新知讲解
幼苗移植会有哪些可能结果?
概率
成活
不成活
两种结果可能性是否相等未知
利用频率估计概率
不能用列举法
某林业部门要考察某种幼树在一定条件下的移植成活率,应采用什么具体做法?
新知讲解
如何利用频率去估计幼树移植的成活率呢?
在相同条件下,对这种幼树进行大量移植,并统计成活数m的情况,计算成活的频率.随着移植数n越来越大,频率会越来越稳定,于是就可以把频率作为成活率的估计值.
实际上有的实验做起来非常麻烦,并且大量的进行这个实验也是不可能的,这就需要“模拟实验”来代替.
新知讲解
下表是一张模拟的统计表,请补全表中空缺,并回答:随着移植数的增加,幼树移植成活的频率有什么趋势?是否能够据此估计出幼树移植成活的概率?
移植总数 n 成活数 m 成活的频率
(结果保留小数点后三位)
10 8 0. 800
50 47
270 235 0. 870
400 369
750 662
1 500 1 335 0. 890
3 500 3 203 0. 915
7 000 6 335
9 000 8 073
14 000 12 628 0. 902
0. 940
0. 923
0. 883
0. 905
0. 897
新知讲解
从表中可以发现,随着移植数的增加,幼树移植成活的频率越来越稳定.当移植总数为14000时,成活的频率为0.902,于是可以估计幼树移植成活的概率为____.
0.9
归纳总结
一般可以用试验次数累计最多时的频率作为概率的估计值.概率估计值小数点后保留的位数不超过频率小数点后保留的位数.
注意
典例精析
某水果公司以2元/kg的成本价新进10 000kg柑橘.如果公司希望这些柑橘能够获得利润5000元,那么在出售柑橘(去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
1、出售柑橘(去掉损坏的柑橘)定价时需要注意哪些问题?
柑橘在运输、储存中会有损坏,公司必须估算出可能损坏的柑橘总数,以便将损坏的柑橘的成本折算到没有损坏的柑橘的售价中,才能保证实际获得的利润.
典例精析
请补全表中空缺,并完成填空(结果保留三位小数):
柑橘总质量 n / 千克 损坏柑橘质量 m / 千克 柑橘损坏的频率(m/n)
50 5.50 0.110
100 10.50 0.105
150 15.15
200 19.42
250 24.25
300 30.93
350 35.32
400 39.24
450 44.57
500 51.54
0.101
0.097
0.097
0.103
0.101
0.098
0.099
0.103
典例精析
若柑橘没有损坏,要获得 5 000 元利润应如何定价?
柑橘损坏后,柑橘的重量减少了,为了确保获得5 000 元利润,定价应如何变化?如何知道柑橘的重量将减少多少?
随着统计的频率越来越稳定,柑橘的损坏率为 0.1,
则柑橘的完好概率为 0.9.
设每千克柑橘的售价为x 元,
根据“利润=(售价-实际成本) 完好的质量”列方程求解.
典例精析
解:销售人员已经对柑橘损坏率进行了抽样统计,填完表格后可以看出,随着柑橘质量的增加,柑橘损坏的频率越来越稳定.柑橘总质量为 500 kg 时的损坏频率为 0.103,于是可以估计柑橘损坏的概率约为 0.1(结果保留小数点后一位).由此可知,柑橘完好的概率为0.9.
典例精析
根据估计的概率可以知道,在10000kg柑橘中完好柑橘的质量为
10000×0.9=9000(kg)
完好柑橘的实际成本为
= ≈2.22(元/kg)
设每千克柑橘的售价为x元,则
(x-2.22)×9000=5000,解得 x≈2.8
因此,出售柑橘时,每千克定价大约2.8元可获利润5000元.
归纳总结
在大量的重复试验中,随机事件发生的频率会呈现出明显的规律性:随着试验次数的增加,频率将会越来越集中在一个常数附近,具有稳定性.概率是频率的稳定值,而频率是概率的近似值.
课堂练习
【知识技能类作业】必做题:
1. 某林业局将一种树苗移植成活的情况绘制成如下统计图,由此可估计这种树苗移植成活的概率约为( )
A. 0.95 B. 0.90 C. 0.85 D. 0.80
2.一个暗箱里放有a个除颜色外完全相同的球,这a个球中红球只有4个,若每次将球搅匀后,任意摸出1个球记下颜色再放回暗箱,通过大量重复摸球实验后发现,摸到红球的频率稳定在20%附近,那么可以推算出a大约是( )
A.25 B.20 C.15 D.10
B
B
课堂练习
【知识技能类作业】必做题:
3.在围棋盒中有x颗白色棋子和y颗黑色棋子,从盒中随机取出一颗棋子,取得白色棋子的概率是.如果再往盒中放进12颗白色棋子,取得白色棋子的概率是,则原来盒中有白色棋子有_____颗.
4.为了估计鱼塘中鱼的条数,养鱼者首先从鱼塘中打捞30条鱼做上标记,然后放归鱼塘,经过一段时间,等有标记的鱼完全混合于鱼群中,再打捞200条鱼,发现其中带标记的鱼有5条,则鱼塘中估计有_______条鱼.
4
1200
课堂练习
【知识技能类作业】选做题:
5.为了比较甲、乙两鱼池中的鱼苗数目,小明从两鱼池中各捞出100条鱼苗,每条做好记号,然后放回原鱼池;一段时间后,在同样的地方,小明再从甲、乙两鱼池中各捞出100条鱼苗,发现其中有记号的鱼苗分别是5条、10条,可以初步估计鱼苗数目较多的是哪个鱼池
课堂练习
【知识技能类作业】选做题:
解:设甲鱼池鱼的总数为x条,则
鱼的概率近似,解得x=2000;
设乙鱼池鱼的总数为y条,则
鱼的概率近似,解得y=1000;
,
可以初步估计鱼苗数目较多的是甲鱼池
课堂练习
【综合拓展类作业】
6.“网红”长沙入选2021年“五一”假期热门旅游城市.本市某景点为吸引游客,设置了一种游戏,其规则如下:凡参与游戏的游客从一个装有12个红球和若干个白球(每个球除颜色外,其他都相同)的不透明纸箱中,随机摸出一个球,摸到红球就可免费得到一个景点吉祥物.据统计参与这种游戏的游客共有60000人,景点一共为参与该游戏的游客免费发放了景点吉祥物15000个.
(1)求参与该游戏可免费得到景点吉祥物的频率;
(2)请你估计纸箱中白球的数量接近多少?
课堂练习
【综合拓展类作业】
解:(1)由题意得:15000÷60000=0.25 ,
答:参与该游戏可免费得到景点吉祥物的频率为0.25 ;
(2)设纸箱中白球的数量为 x个,
由(1)可知,随机摸出一个球是红球的概率约为0.25 ,
则 ,
解得x=36 ,
经检验, x=36是所列分式方程的解,且符合题意,
答:纸箱中白球的数量接近36个.
课堂总结
注意:
用频率估计概率:
在相同条件下,做大量重复试验,事件发生的频率会越来越稳定,我们可以把频率作为概率的估计值.
一般可以用试验次数累计最多时的频率作为概率的估计值.概率估计值小数点后保留的位数不超过频率小数点后保留的位数.
用
频
率
估
计
概
率
板书设计
用频率估计概率:
在相同条件下,做大量重复试验,事件发生的频率会越来越稳定,我们可以把频率作为概率的估计值
作业布置
【知识技能类作业】必做题:
1.一个不透明的袋子中装有2个红球和若干个黄球,这些球除颜色外都相同.经过多次试验发现,摸出红球的频率稳定在 左右,则袋子中的黄球个数最有可能是( )
A.1 B.2 C.4 D.6
2.在一个不透明的袋中装有若干个红球和4个黑球,每个球除颜色外完全相同.摇匀后从中摸出一个球,记下颜色后再放回袋中.不断重复这一过程,共摸球100次.其中有40次摸到黑球,估计袋中红球的个数是 .
B
6
作业布置
【知识技能类作业】选做题:
3.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同,小刚通过多次摸球试验后发现其中摸到红色,黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是 个.
4.某鱼塘里养了1600 条鲤鱼、若干条草鱼和 800条罗非鱼,该鱼塘主通过多次捕捞试验后发现,捕捞到草鱼的频率稳定在 0.5左右,若该鱼塘主随机在鱼塘捕捞一条鱼,则捞到鲤鱼的概率约为 .
24
作业布置
【综合拓展类作业】
5.小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,他在封闭图形内划出了一个半径为1米的圆,在不远处向图形内掷石子,且记录如下:
作业布置
【综合拓展类作业】
(1)随着次数的增多,小明发现m与n的比值在一个常数k附近波动,请你写出k的值.
(2)请利用学过的知识求出封闭图形ABC的大致面积.
作业布置
【综合拓展类作业】
(1)根据统计表,可得石子落在圆内的概率与落在阴影部分的概率之比k= = ;
(2)石子落在圆内和石子落在阴影内的次数关系,随着试验次数的增多,逐渐趋向于为1:2,
所以圆的面积约占封闭图形ABC面积的 ,
因为S圆=π,
所以封闭图形ABC的面积约为3π.
同课章节目录
