人教版数学8年级下册 17.1勾股定理(1) 学案(含答案)
文档属性
| 名称 | 人教版数学8年级下册 17.1勾股定理(1) 学案(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 81.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 00:00:00 | ||
图片预览

文档简介
勾股定理
班级:_____________姓名:__________________组号:_________
第一课时
1.三角形的三边关系是____________________________________________________
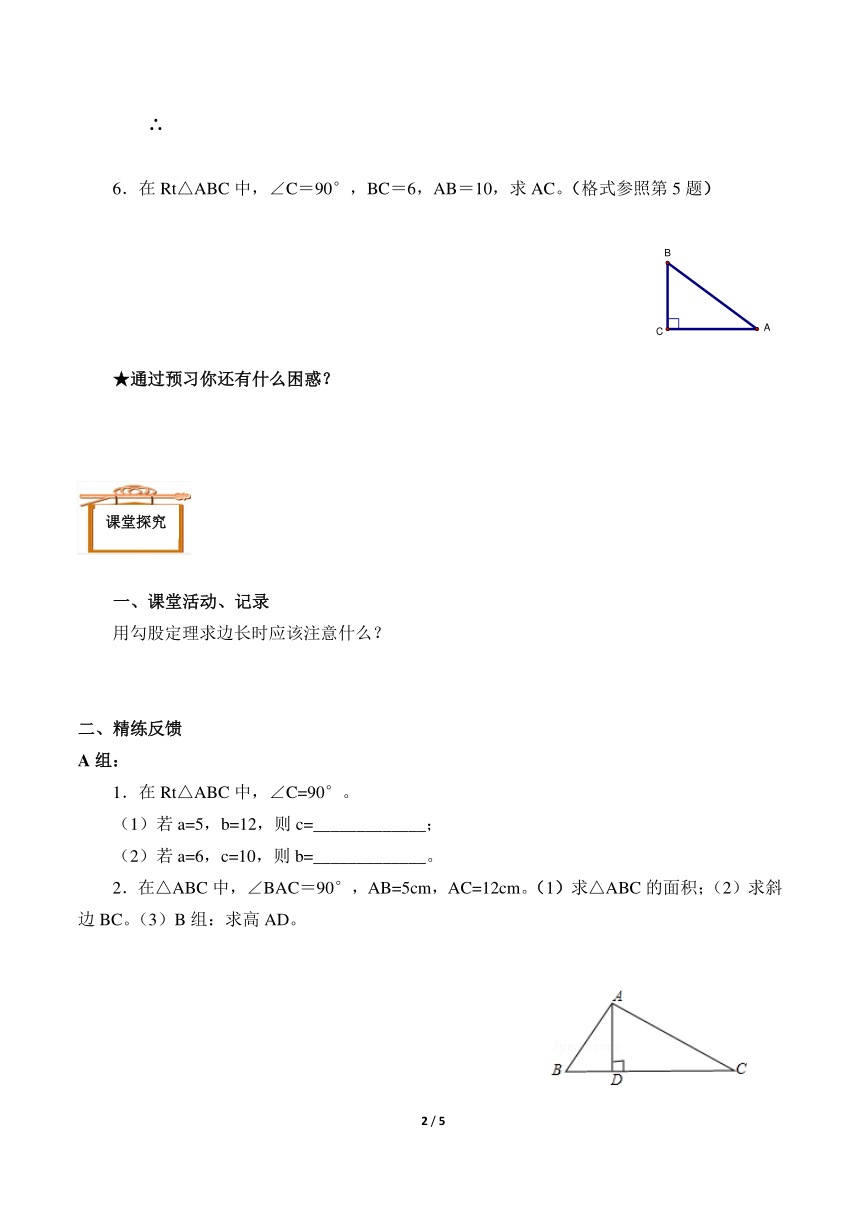
2.如图,已知在Rt△ABC中,,AC=4,BC=3,如何求AB的长?
3.如图,每个小方格的面积的表示1平方厘米。
(1)观察右图1猜想正方形P、Q、R三者之间的面积关系?
(2)思考图中等腰直角△ABC斜边的AB的平方与AC的平方BC的平方之间有什么关系?
(3)通过正方形P、Q、R的面积之间的关系你能发现三边长度之间存在什么关系?
根据面积间关系,对比两种表示方法,列出一个等式:__________________________
4.概括:对于任意的直角三角形,如果它的两条直角边分别为a,b,斜边为c,那么一定有_____________即________________________________________。(文字表达)该命题称为勾股定理。
5.如图,已知在Rt△ABC中,,AC=4,BC=3,求AB的长。
解:∵在Rt△ABC中,∠C=90°,BC=_____________
∴
∴
6.在Rt△ABC中,∠C=90°,BC=6,AB=10,求AC。(格式参照第5题)
★通过预习你还有什么困惑?
一、课堂活动、记录
用勾股定理求边长时应该注意什么?
二、精练反馈
A组:
1.在Rt△ABC中,∠C=90°。
(1)若a=5,b=12,则c=_____________;
(2)若a=6,c=10,则b=_____________。
2.在△ABC中,∠BAC=90°,AB=5cm,AC=12cm。(1)求△ABC的面积;(2)求斜边BC。(3)B组:求高AD。
B组:
3.已知一等腰三角形底边长为10,腰长为13,则腰上的高为_____________。
三、课堂小结
1.在直角三角形中,已知两边求第三边。
2.在运用够定理时应注意的问题?
3.你的其他收获。
四、拓展延伸(选做题)
1.在Rt△ABC中,∠CAB=90°,AD⊥BC,AB=6,AC=8,则BD=_____________,AD=_____________。
2.已知,如图,△ABC三边长分别为AB=15,AC=20,BC=25,求△ABC的面积。
3.△ ABC中,AB=15,AC=13,高AD=12,求△ABC的周长。
【答案】
【学前准备】
1.两边之和大于第三边,两边之差小于第三边
2.解:在Rt△ABC中,∠C=90°,AC=4,BC=3
∴
3.(1)P+Q=R
(2)
(3)P+Q=R
4.;斜边的平方等于两直角边的平方和
5.解:∵在Rt△ABC中,∠C=90°,BC=3,
∴。
∴。
6.解:∵在Rt△ABC中,∠C=90°,BC=6,AB=10
∴
∴
【课堂探究】
课堂活动、记录
略
精练反馈
1.(1)13(2)8
2.(1)∵在△ABC中,∠BAC=90°
(2)
(3)∵
3.12
课堂小结
略
拓展延伸
1.10;4.8
2.
3.在Rt△ADC中
在Rt△ADB中
学前准备
课堂探究
4 / 5
班级:_____________姓名:__________________组号:_________
第一课时
1.三角形的三边关系是____________________________________________________
2.如图,已知在Rt△ABC中,,AC=4,BC=3,如何求AB的长?
3.如图,每个小方格的面积的表示1平方厘米。
(1)观察右图1猜想正方形P、Q、R三者之间的面积关系?
(2)思考图中等腰直角△ABC斜边的AB的平方与AC的平方BC的平方之间有什么关系?
(3)通过正方形P、Q、R的面积之间的关系你能发现三边长度之间存在什么关系?
根据面积间关系,对比两种表示方法,列出一个等式:__________________________
4.概括:对于任意的直角三角形,如果它的两条直角边分别为a,b,斜边为c,那么一定有_____________即________________________________________。(文字表达)该命题称为勾股定理。
5.如图,已知在Rt△ABC中,,AC=4,BC=3,求AB的长。
解:∵在Rt△ABC中,∠C=90°,BC=_____________
∴
∴
6.在Rt△ABC中,∠C=90°,BC=6,AB=10,求AC。(格式参照第5题)
★通过预习你还有什么困惑?
一、课堂活动、记录
用勾股定理求边长时应该注意什么?
二、精练反馈
A组:
1.在Rt△ABC中,∠C=90°。
(1)若a=5,b=12,则c=_____________;
(2)若a=6,c=10,则b=_____________。
2.在△ABC中,∠BAC=90°,AB=5cm,AC=12cm。(1)求△ABC的面积;(2)求斜边BC。(3)B组:求高AD。
B组:
3.已知一等腰三角形底边长为10,腰长为13,则腰上的高为_____________。
三、课堂小结
1.在直角三角形中,已知两边求第三边。
2.在运用够定理时应注意的问题?
3.你的其他收获。
四、拓展延伸(选做题)
1.在Rt△ABC中,∠CAB=90°,AD⊥BC,AB=6,AC=8,则BD=_____________,AD=_____________。
2.已知,如图,△ABC三边长分别为AB=15,AC=20,BC=25,求△ABC的面积。
3.△ ABC中,AB=15,AC=13,高AD=12,求△ABC的周长。
【答案】
【学前准备】
1.两边之和大于第三边,两边之差小于第三边
2.解:在Rt△ABC中,∠C=90°,AC=4,BC=3
∴
3.(1)P+Q=R
(2)
(3)P+Q=R
4.;斜边的平方等于两直角边的平方和
5.解:∵在Rt△ABC中,∠C=90°,BC=3,
∴。
∴。
6.解:∵在Rt△ABC中,∠C=90°,BC=6,AB=10
∴
∴
【课堂探究】
课堂活动、记录
略
精练反馈
1.(1)13(2)8
2.(1)∵在△ABC中,∠BAC=90°
(2)
(3)∵
3.12
课堂小结
略
拓展延伸
1.10;4.8
2.
3.在Rt△ADC中
在Rt△ADB中
学前准备
课堂探究
4 / 5
