3.2 基本不等式 课件(共96张PPT)
文档属性
| 名称 | 3.2 基本不等式 课件(共96张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 129.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 21:29:30 | ||
图片预览











文档简介
(共96张PPT)
第3章 不等式
3 . 2
基本不等式≤ (a,b≥0)
把一个物体放在天平的一个盘子上,在另一个盘子上放砝码使天平平衡,称得物体的质量为 a .如果天平制造得不精确,天平的两臂长略有不同(其他因素不计),那么 a 并非物体的实际质量. 不过,我们可作第二次测量:
把物体调换到天平的另一个盘子上,
此时称得物体的质量为 b. 那么如何合
理地表示物体的质量呢
简单的做法是,把两次称得物体的质量“平均”一下,以
A=
表示物体的质量. 这样的做法合理吗
设天平的两臂长分别为 l1,l2,物体实际质量为 M,根据力学原理有
l1M = l2a,
l2M = l1b.
将上述两个等式的两边分别相乘,得
l1l2M2=l1l2ab,
所以 M=.
由此可知,物体的实际质量是.
对于正数 a,b,我们把 称为 a,b 的算术平均数,
称为 a,b 的几何平均数.
算术平均数与几何平均数
● 两个正数 a,b 的算术平均数和几何平均数之间具有怎样的大小关系
3 . 2 . 1
基本不等式的证明
当a>0,b>0时,我们可以尝试作出长度为 和 的两条线段,再比较这两条线段的长.
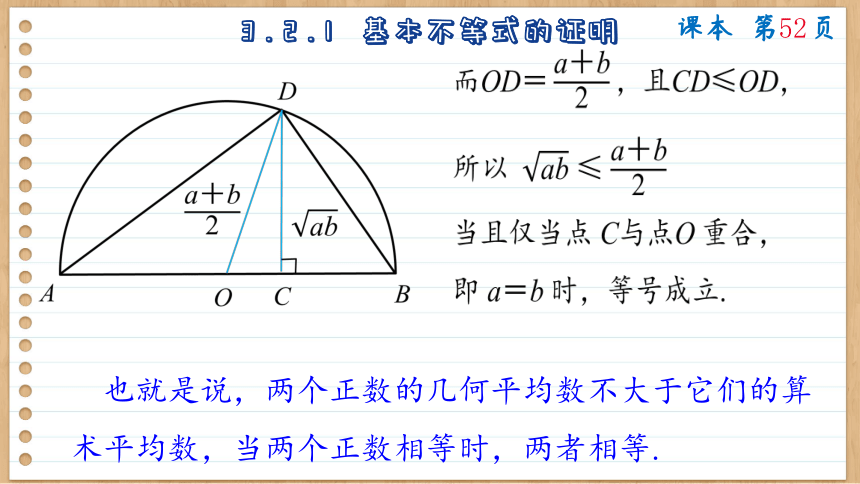
如图,AB是⊙O 的直径,AC=a,CB=b,过点 C作CD⊥AB 交⊙O 的半圆于点 D,连接 AD,BD,易知 △ACD∽△DCB,故 =,得CD=.
而OD=,且CD≤OD,
所以 ≤
当且仅当点 C与点O 重合,即 a=b 时,等号成立.
也就是说,两个正数的几何平均数不大于它们的算术平均数,当两个正数相等时,两者相等.
下面证明上述猜想是正确的.
证法 1
对于正数 a,b,有
-
= (a+b-2)
= [()2+()2-2]
= (-)2.
因为(-)2 ≥ 0,
所以≥0 ,
即≤ .
当且仅当 = ,
即a=b时,等号成立.
证法 2
对于正数 a,b,要证 ≤ .
只要证 2≤ a+b,
只要证 0≤a-2+b,
只要证 0≤(-)2.
因为最后一个不等式成立,所以 ≤ 成立,当且仅当 a=b 时,等号成立.
证法 3
对于正数 a,b,有
(-)2≥0,
a+b-2≥0,
a+b≥2,
≥a+b.
当且仅当 a=b 时,等号成立.
(1) 公式:
① 条件:a,b是正数;
② 结论:____________;
③ 等号成立:当且仅当 a=b 时.
一、基本不等式
≤
当 a,b≥0时,这个不等式仍然成立.
我们把不等式≤ (a,b≥0) 称为基本不等式.
(2) 本质:
基本不等式表明,两个正数的算术平均数 不小于它们的几何平均数 .
(3) 变形式:
当 a,b∈R 时,由(a-b)2≥0可得
a2+b2≥2ab,a2+b2+2ab≥4ab,
即 ≥ab,()2≥ab,
当且仅当 a=b时,其中的等号成立.
当 a>0,b>0 时,请用基本不等式证明这两个不等式.
从而得到:
当 a,b∈R 时,
ab≤ (当且仅当 a=b 时,等号成立);
ab≤()2 (当且仅当 a=b 时,等号成立).
这两个不等式通常可以直接使用.
【思考】
(1) 基本不等式成立的条件能省略吗
提示:基本不等式成立的条件“a>0,b>0”不能省略,例如 ≥ 是不成立的.
(2)“当且仅当 a=b 时,等号成立”的含义是什么
提示:一方面是当a=b时取等号,即
a=b =;
另一方面是仅当a=b时取等号,即
= a=b.
二、基本不等式求最值的结论 *
对于正数 a,b,
(1) 和 a+b 为定值时,积 ab 有最_____值;
积 ab 为定值时,和 a+b 有最______值.
(2) 取等号的条件:当且仅当________时,=.
(3) 应用:求和式的最小值,乘积式的最大值.
大
小
a=b
例 1
设 a,b 为正数,证明下列不等式成立:
(1) + ≥2;
(2) a+b++ ≥4;
(1) + ≥2;
证明: 因为 a,b 为正数,所以 , 也为正数.
由基本不等式,得
+ ≥2 =2,
当且仅当 = ,即 a=b 时,取得等号.
所以原不等式成立.
证明: 因为 a,b 为正数,所以 , 也为正数.
由基本不等式,得
a+≥2 =2,
b+≥2 =2
(2) a+b++ ≥4;
所以 a+b++ ≥4,
当且仅当 a=,b= 时,即a=b=1时,取得等号.
因此,原不等式成立.
例 2
设 y=x+,x∈(-2,+∞),求y的最小值.
解:因为 x>-2,所以 x+2>0.
由基本不等式,得 x+ = (x+2)+-2
≥2=6,
当且仅当 x+2= ,即 x=2时,等号成立.
因此,当 x=2 时,y的最小值为6.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 对任意 a,b∈R,a2+b2≥2ab,a+b≥2 均成立. ( )
任意 a,b∈R,有a2+b2≥2ab成立,当 a,b 都为正数时,不等式 a+b≥2 成立.
(2) 若 a≠0,则 a+ ≥ 2 =4. ( )
(3) 若a>0,b>0,则 ab≤()2. ( )
只有当a>0时,根据基本不等式,才有不等式a+ ≥ 2 =4 成立.
2. 不等式 (x-2y)+≥2 成立的前提条件为 ( )
A. x≥2y B. x>2y C. x≤2y D. x<2y
B
解析:因为不等式成立的前提条件是各项均为正,
所以 x-2y>0,即 x>2y .
解析
3. 设 x,y 满足 x+y=40,且 x,y 都是正数,则
xy 的最大值为_________.
400
解析:因为 x,y 都是正数,且 x+y=40,
所以 xy ≤()2=400,
当且仅当 x=y=20 时取等号.
解析
【跟踪训练】
1. 已知 ab=4,a>0,b>0,则 a+b 的最小值为( ).
A.1 B.2 C.4 D.8
C
解析:因为 a>0,b>0,所以 a+b≥2=4,
当且仅当 a=b=2时取等号,
故 a+b的最小值为4.
解析
2. 若 x2+y2=2,则 xy 的最大值是 ( )
A. B.1 C.2 D.4
B
解析:xy≤= 1,当且仅当 x=y 时取“=”.
解析
3. 设 a>b>0,则下列不等式中一定成立的是 ( )
A. a-b<0 B. 0<<1
C. < D. ab>a+b
C
解析:因为a>b>0,
由基本不等式知< 一定成立.
解析
4. 若 0<x<1,则 的取值范围是
________________________.
0<≤
解析:由0<x<1知 3-2x>0,
故=·≤·=,
当且仅当x=时,上式等号成立.
所以 0<≤.
解析
5. 已知 a,b 是不相等的正数,x= ,y=,
则 x,y 的大小关系为________.
x<y
解析:因为 a,b 是不相等的正数,
所以 x2= <=a+b=y2,
又x>0,y>0,所以 x<y.
解析
练 习
1. 计算下列两个数的算术平均数与几何平均数
(其中p>0):
(1) 2,8; (2) 3,12; (3) p,9p; (4) 2,2p2.
解:(1) 2,8 的算术平均数为5,几何平均数为4;
(2) 3,12 的算术平均数为,几何平均数为6;
(3) p,9p; (4) 2,2p2.
解:(3) p,9p的算术平均数为5p,几何平均数为3p;
(4) 2,2p2的算术平均数为1+p2,
几何平均数为2p;
2. 如图,我国古代的“弦图”是由四个全等的直角三角
形围成的. 设直角三角形的直角边长为 a,b,根据图
示,大正方形的面积与四个小直角三角形的面积之和
存在不等关系,用 a,b 表示这种关系.
解:由题意,直角三角形的斜边长为,则大正方形面积 S1=a2+b2
四个直角三角形的面积为 S2 = 4×ab =2ab,
则 a2+b2≥2ab,当且仅当a=b时,等号成立.
3. 证明:
(1) a+ ≥3(a>1);
证明:∵a>1,
∴a+=a-1+ +1
≥2 +1 =3,
当且仅当a-1=,
即a=2 (a>1)时等号成立;
(2) x+ ≤-2 (x<0).
证明:∵ x<0,
∴ x+=-(-x+)
≤-2 =-2,
当且仅当-x=,
即x=-1 (x<1)时等号成立;
4. 求 4x2+ 的最小值.
解:由4x2, 均大于0,
∴ 4x2+ ≥2 =2 =12,
当且仅当 4x2= 时取得最小值,故x=,
即 4x2+ 是的最小值为12,此时x为.
5. 设 0° < α < 90°利用直角三角形三边关系,证明
1 < sinα + cosα ≤ .
证明:∵ 0°<α<90°,
∴ 0°<2α<180°,
∴ sin2α∈(0,1],
∴ 1+sin2α∈ (1,2],
∴ (sinα+cosα)2∈ (1,2],
∴ 1< (sinα+cosα)2≤2,
∴ 1< (sinα+cosα)2≤2,得证.
3 . 2 . 2
基本不等式的应用
基本不等式 ≤ (a,b>0) 常用于证明一些不等式以及求某些函数的最大值或最小值.
例 3
用长为 4a 的铁丝围成一个矩形,怎样才能使所围矩形的面积最大
解: 设矩形长为 x (0<x< 2a),则宽为 2a-x,矩形面积为 S=x(2a-x),
且 x>0,2a-x>0.
由基本不等式,得 ≤=a.
上式当且仅当 x=2a-x,即 x=a 时,等号成立.
由此可知,当x=a时,S=(2a-x)取得最大值 a2.
答 将铁丝围成正方形时面积最大,最大面积为 a2.
例 4
某工厂建造一个无盖的长方体贮水池,其容积为4 800 m,深度为 3m. 如果池底每平方米的造价为 150 元,池壁每平方米的造价为 120 元,怎样设计水池能使总造价最低 最低总造价为多少元
解 设总造价为 y 元 (y>0,池底的一边长为 x m (a>0),
则另一边长为m,即 m.
由题中条件可得 y =150×+2×120×3×(x+)
= 150×1600+720 (x+)
由题意知 x>0,及x+≥2=80 (当且仅当 x =40时,等号成立), 所以 y≥150×1600+720×80= 297 600,且x=40时,取得等号.
答 当水池设计成底面边长为 40 m 的正方形时,总造价最低为297 600 元.
(1) 和 a+b 为定值时,积 ab 有最大值 (如例 3);
ab 为定值时和 a+b有最小值 (如例 4).
(2) 取等号的条件 (当且仅当 a=b时, =).
对于正数 a,b,在运用基本不等式时,应注意:
例 5
如图3-2-2,在△ABC中,∠ACB=90°,AC =b,BC=a,且+=1. 当△ABC 的面积最小时,求 a,b 的值.
解 由题意知 a>0,b>0,由基本不等式,得
+ ≥2.
因为+=1,所以1≥2,故 ab>8.
于是,S△ABC= ab ≥ 4,
当且仅当,
即 a=2,b=4时,等号成立.
因此,当△ABC的面积最小时,a=2, b=4.
例 6
如图 3-2-3,一份印刷品的排版面积(矩形)为 A,它的两边都留有宽为 a 的空白,顶部和底部都留有宽为的空白如何选择纸张的尺寸,才能使纸的用量最少
解 设纸张的面积为 S,排版矩形的长和宽分别是 x,y (x>0,y>0),则 xy=A.
S= (x+2a)(y+2b)
= xy+2bx +2ay+4ab
≥ xy+2+4ab
= A+4+4ab
=(+2)2.
当且仅当 2bx=2ay,即 x=,y=时,S 有最小值(+2)2,
此时纸张的长和宽分别为 +2a 和 +2b.
答 当纸张的长和宽分别为 +2a 和 +2b时,纸张的用量最少.
【跟踪训练】
1. 若 a>0,b>0,且 a+b=4,则下列不等式恒成立的是( )
A. B. +≤1 C. ≥2 D. a2+b2≥8
D
解析:4=a+b≥2 (当且仅当a=b时,等号成立),即≤2,ab≤4, ≥ ,A,C不成立; + = = ≥1,B不成立;a2+b2= (a+b)2-2ab=16-2ab≥8.
解析
2. 若 x>0,y>0,且 + = 1,则 xy 有 ( )
A.最大值64 B.最小值
C.最小值 D.最小值64
D
解析:由题意,得 xy=(+)xy=2y+8x≥2=8 ,所以≥8,即 xy 有最小值64,
等号成立的条件是 x=4,y=16.
解析
3.设 0<x<2,则函数 y=的最大值为_____.
4
解析:因为0<x<2,
所以0<3x<6,8-3x>2>0,
所以 y= ≤ =4,
当且仅当3x=8-3x,即 x=时,取等号.
所以当 x=时,y=有最大值4.
解析
4. 某游泳馆出售冬季游泳卡,每张240元,其使用规定:不记名,每卡每次只限一人,每天只限一次.某班有48名同学,老师打算组织同学们集体去游泳,除需购买若干张游泳卡外,每次游泳还需包一辆汽车,无论乘坐多少名同学,每次的包车费均为40元. 若使每名同学游8次,每人最少应交多少元钱
解:设买x张游泳卡,总开支为y元,则每批去x名同学,共需去批,总开支又分为:①买卡所需费用240x,②包车所需费用×40.
所以 y=240x+×40 (0<x≤48,x∈Z).
所以 y=240 (x+)≥240×2= 3 840,
当且仅当x=,即 x=8时取等号.
故每人最少应交 =80(元).
练 习
1. 若m>0,n>0,mn=81,则m+n的最小值是( ).
A. 4 B. 4
C. 9 D. 18
D
2. 若直角三角形的面积为 50,则两条直角边的和的最
小值是( ).
A. 5 B.10
C. 10 D.20
D
3. 设 x>0,y>0,且 2x+5y=20,求xy的最大值.
解:∵ x>0,y>0,且 2x+5y=20.
∴ 20≥2,化为:xy≤10,
当且仅当2x=5y=10时取等号.
∴ xy 的最大值为10.
4. 将一段圆木制成横截面是矩形的柱子,怎样加工才能
使横截面的面积最大
解:如图所示,矩形ABCD为横截面设圆木的半径为r,∠CAB=α ,(0<α<),
故 AB=2rcosα,BC=2rsinα,
故 S=4r2sinαcosα=2r2sin2α≤2r2,
故当α=45°时,sin2α 取得最大值1,
此时面积 S 取得最大值 S=2r2.
5. 如图,质量是 W 的重物挂在杆上距支点 a 处. 质量均
的杆子每单位长度的质量为 m. 杠杆应当多长,才能
使得加在另一端用来平衡重物的力 F最小
解:设杠杆长为x米时,在另一端用来平衡重物的力F最小,杆子质量均匀且每单位长度的质量为m,故杆的质量为 x×m.
则 W×a+x×mg× =F·x,
∴ F=+=( -)2 +.
当且仅当 = 时,即
x= 时,力 F有最小值;
所以杠杆应当为 时,才能使得加在另一端用来平衡重物的力F最小。
习题 3.2
感受·理解
1. 证明下列不等式:
(1) a2+b2≥2a+2b-2;
证明:∵a2+1>2a,b2+1>2b,
∴ a2+b2+2≥2a+2b,
即 a2+b2≥2a+2b-2.
(2) ()2 ≤ ;
证明:∵ 2ab≤a2+b2,
∴ ()2=a2+2ab+b2≤=,
即 ()2 ≤ .
(3) 若 a,b ∈(0,+∞),则 ≤ .
证明:∵ a,b∈(0,+∞),
∴ 2≤a+b,
从而 ≤1,故 =≤.
2. 设 x>0,y>0,且 xy=4,求的最小值.
解:∵ x>0,y>0,xy=4,
∴ y=,∴ += + ≥2 =1,
当且仅当 = , xy=4,x>0,y>0.
即x=y=2 时取等号.
∴ + 的最小值是1.
3. 证明:
(1) x2+ ≥1;
证明:∵ x2+1>0,
∴ x2+=(x2+1)+-1
≥2-1=1,
即 x2+ ≥1. 当且仅当 x2+1= ,
即 x=0 时,取得等号.
(2) >2;
证明:∵==+
≥2 = 2,
当且仅当 = 时,等号成立.
∵ 对任意的实数x, ≠,∴ >2.
4. 求 1+2x2+ 的最小值.
解:1+2x2+ ≥1+2 =9
当且仅当 2x2= 即 x=±时等号成立.
∴ 1+2x2+ 的最小值为9.
5. 设 a,b 是正实数,求证:(a+)(b+)≥4.
解:∵ a>0,b>0,
∴ a+ ≥2 =2,
当且仅当 a=,即 a=1 时取等号.
∴ b+ ≥2 =2,
当且仅当 b =,即 b=1 时取等号.
∴ (a+)(b+) ≥2×2 =4,
当且仅当 a=b=1时取等号.
综上, (a+)(b+)≥4.
6. 如图,墙角线互相垂直,长为 a m 的木棒AB的两个端
点分别在这两墙角线上,如何放置木棒才能使围成区
域的面积最大
解:如图,设 AO=a m,BO=y m.
∵OA⊥OB
∴ OA2+OB2=AB2
∴ x2+y2=a2
∵(x-y)2≥0
∴ x2-2xy+y2≥0
∴ x2+y2≥2xy
∴ xy≤ (x2+y2), 即xy的最大值为 (x2+y2),
∵当 x=y 时, (x-y)2=0,
∴当 x=y 时, xy= (x2+y2),
即当 x=y 时,xy 的值最大,
∵ S△AOB=xy.
∴当 x=y 时,S△AOB面积最大,
由 x2+x2=a2 得 x=a
∴ 当OB=OA=a m 时,
木棒围成区域的面积最大.
7. 已知 a,b,c,d 都是正数,且 a<b,c<d,求证:
< .
证明:设点A(b,a),B(-c,-c),C(-d,-d),
∵a>0,b>0,c>0,d>0,
∴点A在第一象限,点B在第三象限,
点C第三象限,
且点B、点C都在直线 y=x上,
∵c<d,∴点B在点C的右上方,
∵a<b,∴点A在直线y=x (第一象限内)的下方,
在直角坐标系中表示出点A、点B、点C,
的几何意义是点A与点B连线的斜率,
的几何意义是点A与点C连线的斜率,
由图象可以看出直线AC的斜率更大,则 < .
思考·运用
8. 当 x≠0时,求 x+ 的取值范围.
解:当x>0时,x+ ≥2 =4,
∴当且仅当 x= 即 x=2 时等号成立;
当 x<0时, -x>0
∴ -x- ≥2 =4
∴ x+ ≤-4
∴当且仅当-x=- 即 x=-2 时等号成立,
∴ 综上所述, x+ 的取值范围为:
(-∞,-4)∪(4,+∞)
9. 如图,电路中电源的电动势为E,内阻为 r,R1为固定
电阻,R2是一个滑动变阻器. 已知 R2消耗的电功率为
P=()2R2. 当R2调至何值时, ()2R2
最大 最大值是多少
解:∵P=()2R2 =
=,
且 ≥2 =2;
∴P≤,当且仅当,
即 r+R1= R2时取等号,
∴当 r+R1= R2, P取得最大值,最大值是.
10. 某种产品的两种原料相继提价,产品生产者决定根
据这两种原料提价的百分比,对产品分两次提价,
现在有三种提价方案:
方案甲:第一次提价 p%,第二次提价 q%;
方案乙:第一次提价 q%,第二次提价 p%;
方案丙:第一次提价 %,第二次提价%.
其中p>q>0,比较上述三种方案,哪一种提价少
哪一种提价多
解:设提价前的价格为1,那么两次提价后的价格为,
方案甲:(1+p %)(1+q%)
=1+p%+q%+0.01pq%;
方案乙:(1+q%)(1+p%)
= 1+p%+q% +0.01pq%;
方案丙:(1+%) (1+%)
=1+p% +q% +(%)
=1+ p%+q% +0.01 ×()2%;
∵ ()2 ≥pq,且 p>q>0,
∴ 上式“=”不成立;
∴ 方案乙提价少,方案丙提价多.
探究·拓展
11. (阅读题)甲乙两同学分别解“设 x∈[0,+∞),求函
数 y=2x2+1的最小值”的过程如下:
甲:y=2x2+1≥2=2x,又x≥1,
所以2x>2 .
乙:因为y=2x2-1在区间[1,+∞)上的图象随着x增
大而逐渐上升,即y随x增大而增大,所以y的最
小值是 2×12+1=3.
试判断谁错,错在何处
解:甲的解法错误,乙的解法正确.
甲同学的解法:利用基本不等式法求最小值,
∵ 2x2+1 ≥ 2 = 2,但由于2x,不是定值,
且未考虑取等的问题,所以解法错误.
乙同学的解法:
∵ y=2x2+1在[1,+∞) 上单调递增,
∴ y=2x2+1的最小值是 2×12+1=3,解法正确.
综上所述:甲同学的解析错误,基本不等式应用错误.
本课结束
This lesson is over
THANKS!
第3章 不等式
3 . 2
基本不等式≤ (a,b≥0)
把一个物体放在天平的一个盘子上,在另一个盘子上放砝码使天平平衡,称得物体的质量为 a .如果天平制造得不精确,天平的两臂长略有不同(其他因素不计),那么 a 并非物体的实际质量. 不过,我们可作第二次测量:
把物体调换到天平的另一个盘子上,
此时称得物体的质量为 b. 那么如何合
理地表示物体的质量呢
简单的做法是,把两次称得物体的质量“平均”一下,以
A=
表示物体的质量. 这样的做法合理吗
设天平的两臂长分别为 l1,l2,物体实际质量为 M,根据力学原理有
l1M = l2a,
l2M = l1b.
将上述两个等式的两边分别相乘,得
l1l2M2=l1l2ab,
所以 M=.
由此可知,物体的实际质量是.
对于正数 a,b,我们把 称为 a,b 的算术平均数,
称为 a,b 的几何平均数.
算术平均数与几何平均数
● 两个正数 a,b 的算术平均数和几何平均数之间具有怎样的大小关系
3 . 2 . 1
基本不等式的证明
当a>0,b>0时,我们可以尝试作出长度为 和 的两条线段,再比较这两条线段的长.
如图,AB是⊙O 的直径,AC=a,CB=b,过点 C作CD⊥AB 交⊙O 的半圆于点 D,连接 AD,BD,易知 △ACD∽△DCB,故 =,得CD=.
而OD=,且CD≤OD,
所以 ≤
当且仅当点 C与点O 重合,即 a=b 时,等号成立.
也就是说,两个正数的几何平均数不大于它们的算术平均数,当两个正数相等时,两者相等.
下面证明上述猜想是正确的.
证法 1
对于正数 a,b,有
-
= (a+b-2)
= [()2+()2-2]
= (-)2.
因为(-)2 ≥ 0,
所以≥0 ,
即≤ .
当且仅当 = ,
即a=b时,等号成立.
证法 2
对于正数 a,b,要证 ≤ .
只要证 2≤ a+b,
只要证 0≤a-2+b,
只要证 0≤(-)2.
因为最后一个不等式成立,所以 ≤ 成立,当且仅当 a=b 时,等号成立.
证法 3
对于正数 a,b,有
(-)2≥0,
a+b-2≥0,
a+b≥2,
≥a+b.
当且仅当 a=b 时,等号成立.
(1) 公式:
① 条件:a,b是正数;
② 结论:____________;
③ 等号成立:当且仅当 a=b 时.
一、基本不等式
≤
当 a,b≥0时,这个不等式仍然成立.
我们把不等式≤ (a,b≥0) 称为基本不等式.
(2) 本质:
基本不等式表明,两个正数的算术平均数 不小于它们的几何平均数 .
(3) 变形式:
当 a,b∈R 时,由(a-b)2≥0可得
a2+b2≥2ab,a2+b2+2ab≥4ab,
即 ≥ab,()2≥ab,
当且仅当 a=b时,其中的等号成立.
当 a>0,b>0 时,请用基本不等式证明这两个不等式.
从而得到:
当 a,b∈R 时,
ab≤ (当且仅当 a=b 时,等号成立);
ab≤()2 (当且仅当 a=b 时,等号成立).
这两个不等式通常可以直接使用.
【思考】
(1) 基本不等式成立的条件能省略吗
提示:基本不等式成立的条件“a>0,b>0”不能省略,例如 ≥ 是不成立的.
(2)“当且仅当 a=b 时,等号成立”的含义是什么
提示:一方面是当a=b时取等号,即
a=b =;
另一方面是仅当a=b时取等号,即
= a=b.
二、基本不等式求最值的结论 *
对于正数 a,b,
(1) 和 a+b 为定值时,积 ab 有最_____值;
积 ab 为定值时,和 a+b 有最______值.
(2) 取等号的条件:当且仅当________时,=.
(3) 应用:求和式的最小值,乘积式的最大值.
大
小
a=b
例 1
设 a,b 为正数,证明下列不等式成立:
(1) + ≥2;
(2) a+b++ ≥4;
(1) + ≥2;
证明: 因为 a,b 为正数,所以 , 也为正数.
由基本不等式,得
+ ≥2 =2,
当且仅当 = ,即 a=b 时,取得等号.
所以原不等式成立.
证明: 因为 a,b 为正数,所以 , 也为正数.
由基本不等式,得
a+≥2 =2,
b+≥2 =2
(2) a+b++ ≥4;
所以 a+b++ ≥4,
当且仅当 a=,b= 时,即a=b=1时,取得等号.
因此,原不等式成立.
例 2
设 y=x+,x∈(-2,+∞),求y的最小值.
解:因为 x>-2,所以 x+2>0.
由基本不等式,得 x+ = (x+2)+-2
≥2=6,
当且仅当 x+2= ,即 x=2时,等号成立.
因此,当 x=2 时,y的最小值为6.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 对任意 a,b∈R,a2+b2≥2ab,a+b≥2 均成立. ( )
任意 a,b∈R,有a2+b2≥2ab成立,当 a,b 都为正数时,不等式 a+b≥2 成立.
(2) 若 a≠0,则 a+ ≥ 2 =4. ( )
(3) 若a>0,b>0,则 ab≤()2. ( )
只有当a>0时,根据基本不等式,才有不等式a+ ≥ 2 =4 成立.
2. 不等式 (x-2y)+≥2 成立的前提条件为 ( )
A. x≥2y B. x>2y C. x≤2y D. x<2y
B
解析:因为不等式成立的前提条件是各项均为正,
所以 x-2y>0,即 x>2y .
解析
3. 设 x,y 满足 x+y=40,且 x,y 都是正数,则
xy 的最大值为_________.
400
解析:因为 x,y 都是正数,且 x+y=40,
所以 xy ≤()2=400,
当且仅当 x=y=20 时取等号.
解析
【跟踪训练】
1. 已知 ab=4,a>0,b>0,则 a+b 的最小值为( ).
A.1 B.2 C.4 D.8
C
解析:因为 a>0,b>0,所以 a+b≥2=4,
当且仅当 a=b=2时取等号,
故 a+b的最小值为4.
解析
2. 若 x2+y2=2,则 xy 的最大值是 ( )
A. B.1 C.2 D.4
B
解析:xy≤= 1,当且仅当 x=y 时取“=”.
解析
3. 设 a>b>0,则下列不等式中一定成立的是 ( )
A. a-b<0 B. 0<<1
C. < D. ab>a+b
C
解析:因为a>b>0,
由基本不等式知< 一定成立.
解析
4. 若 0<x<1,则 的取值范围是
________________________.
0<≤
解析:由0<x<1知 3-2x>0,
故=·≤·=,
当且仅当x=时,上式等号成立.
所以 0<≤.
解析
5. 已知 a,b 是不相等的正数,x= ,y=,
则 x,y 的大小关系为________.
x<y
解析:因为 a,b 是不相等的正数,
所以 x2= <=a+b=y2,
又x>0,y>0,所以 x<y.
解析
练 习
1. 计算下列两个数的算术平均数与几何平均数
(其中p>0):
(1) 2,8; (2) 3,12; (3) p,9p; (4) 2,2p2.
解:(1) 2,8 的算术平均数为5,几何平均数为4;
(2) 3,12 的算术平均数为,几何平均数为6;
(3) p,9p; (4) 2,2p2.
解:(3) p,9p的算术平均数为5p,几何平均数为3p;
(4) 2,2p2的算术平均数为1+p2,
几何平均数为2p;
2. 如图,我国古代的“弦图”是由四个全等的直角三角
形围成的. 设直角三角形的直角边长为 a,b,根据图
示,大正方形的面积与四个小直角三角形的面积之和
存在不等关系,用 a,b 表示这种关系.
解:由题意,直角三角形的斜边长为,则大正方形面积 S1=a2+b2
四个直角三角形的面积为 S2 = 4×ab =2ab,
则 a2+b2≥2ab,当且仅当a=b时,等号成立.
3. 证明:
(1) a+ ≥3(a>1);
证明:∵a>1,
∴a+=a-1+ +1
≥2 +1 =3,
当且仅当a-1=,
即a=2 (a>1)时等号成立;
(2) x+ ≤-2 (x<0).
证明:∵ x<0,
∴ x+=-(-x+)
≤-2 =-2,
当且仅当-x=,
即x=-1 (x<1)时等号成立;
4. 求 4x2+ 的最小值.
解:由4x2, 均大于0,
∴ 4x2+ ≥2 =2 =12,
当且仅当 4x2= 时取得最小值,故x=,
即 4x2+ 是的最小值为12,此时x为.
5. 设 0° < α < 90°利用直角三角形三边关系,证明
1 < sinα + cosα ≤ .
证明:∵ 0°<α<90°,
∴ 0°<2α<180°,
∴ sin2α∈(0,1],
∴ 1+sin2α∈ (1,2],
∴ (sinα+cosα)2∈ (1,2],
∴ 1< (sinα+cosα)2≤2,
∴ 1< (sinα+cosα)2≤2,得证.
3 . 2 . 2
基本不等式的应用
基本不等式 ≤ (a,b>0) 常用于证明一些不等式以及求某些函数的最大值或最小值.
例 3
用长为 4a 的铁丝围成一个矩形,怎样才能使所围矩形的面积最大
解: 设矩形长为 x (0<x< 2a),则宽为 2a-x,矩形面积为 S=x(2a-x),
且 x>0,2a-x>0.
由基本不等式,得 ≤=a.
上式当且仅当 x=2a-x,即 x=a 时,等号成立.
由此可知,当x=a时,S=(2a-x)取得最大值 a2.
答 将铁丝围成正方形时面积最大,最大面积为 a2.
例 4
某工厂建造一个无盖的长方体贮水池,其容积为4 800 m,深度为 3m. 如果池底每平方米的造价为 150 元,池壁每平方米的造价为 120 元,怎样设计水池能使总造价最低 最低总造价为多少元
解 设总造价为 y 元 (y>0,池底的一边长为 x m (a>0),
则另一边长为m,即 m.
由题中条件可得 y =150×+2×120×3×(x+)
= 150×1600+720 (x+)
由题意知 x>0,及x+≥2=80 (当且仅当 x =40时,等号成立), 所以 y≥150×1600+720×80= 297 600,且x=40时,取得等号.
答 当水池设计成底面边长为 40 m 的正方形时,总造价最低为297 600 元.
(1) 和 a+b 为定值时,积 ab 有最大值 (如例 3);
ab 为定值时和 a+b有最小值 (如例 4).
(2) 取等号的条件 (当且仅当 a=b时, =).
对于正数 a,b,在运用基本不等式时,应注意:
例 5
如图3-2-2,在△ABC中,∠ACB=90°,AC =b,BC=a,且+=1. 当△ABC 的面积最小时,求 a,b 的值.
解 由题意知 a>0,b>0,由基本不等式,得
+ ≥2.
因为+=1,所以1≥2,故 ab>8.
于是,S△ABC= ab ≥ 4,
当且仅当,
即 a=2,b=4时,等号成立.
因此,当△ABC的面积最小时,a=2, b=4.
例 6
如图 3-2-3,一份印刷品的排版面积(矩形)为 A,它的两边都留有宽为 a 的空白,顶部和底部都留有宽为的空白如何选择纸张的尺寸,才能使纸的用量最少
解 设纸张的面积为 S,排版矩形的长和宽分别是 x,y (x>0,y>0),则 xy=A.
S= (x+2a)(y+2b)
= xy+2bx +2ay+4ab
≥ xy+2+4ab
= A+4+4ab
=(+2)2.
当且仅当 2bx=2ay,即 x=,y=时,S 有最小值(+2)2,
此时纸张的长和宽分别为 +2a 和 +2b.
答 当纸张的长和宽分别为 +2a 和 +2b时,纸张的用量最少.
【跟踪训练】
1. 若 a>0,b>0,且 a+b=4,则下列不等式恒成立的是( )
A. B. +≤1 C. ≥2 D. a2+b2≥8
D
解析:4=a+b≥2 (当且仅当a=b时,等号成立),即≤2,ab≤4, ≥ ,A,C不成立; + = = ≥1,B不成立;a2+b2= (a+b)2-2ab=16-2ab≥8.
解析
2. 若 x>0,y>0,且 + = 1,则 xy 有 ( )
A.最大值64 B.最小值
C.最小值 D.最小值64
D
解析:由题意,得 xy=(+)xy=2y+8x≥2=8 ,所以≥8,即 xy 有最小值64,
等号成立的条件是 x=4,y=16.
解析
3.设 0<x<2,则函数 y=的最大值为_____.
4
解析:因为0<x<2,
所以0<3x<6,8-3x>2>0,
所以 y= ≤ =4,
当且仅当3x=8-3x,即 x=时,取等号.
所以当 x=时,y=有最大值4.
解析
4. 某游泳馆出售冬季游泳卡,每张240元,其使用规定:不记名,每卡每次只限一人,每天只限一次.某班有48名同学,老师打算组织同学们集体去游泳,除需购买若干张游泳卡外,每次游泳还需包一辆汽车,无论乘坐多少名同学,每次的包车费均为40元. 若使每名同学游8次,每人最少应交多少元钱
解:设买x张游泳卡,总开支为y元,则每批去x名同学,共需去批,总开支又分为:①买卡所需费用240x,②包车所需费用×40.
所以 y=240x+×40 (0<x≤48,x∈Z).
所以 y=240 (x+)≥240×2= 3 840,
当且仅当x=,即 x=8时取等号.
故每人最少应交 =80(元).
练 习
1. 若m>0,n>0,mn=81,则m+n的最小值是( ).
A. 4 B. 4
C. 9 D. 18
D
2. 若直角三角形的面积为 50,则两条直角边的和的最
小值是( ).
A. 5 B.10
C. 10 D.20
D
3. 设 x>0,y>0,且 2x+5y=20,求xy的最大值.
解:∵ x>0,y>0,且 2x+5y=20.
∴ 20≥2,化为:xy≤10,
当且仅当2x=5y=10时取等号.
∴ xy 的最大值为10.
4. 将一段圆木制成横截面是矩形的柱子,怎样加工才能
使横截面的面积最大
解:如图所示,矩形ABCD为横截面设圆木的半径为r,∠CAB=α ,(0<α<),
故 AB=2rcosα,BC=2rsinα,
故 S=4r2sinαcosα=2r2sin2α≤2r2,
故当α=45°时,sin2α 取得最大值1,
此时面积 S 取得最大值 S=2r2.
5. 如图,质量是 W 的重物挂在杆上距支点 a 处. 质量均
的杆子每单位长度的质量为 m. 杠杆应当多长,才能
使得加在另一端用来平衡重物的力 F最小
解:设杠杆长为x米时,在另一端用来平衡重物的力F最小,杆子质量均匀且每单位长度的质量为m,故杆的质量为 x×m.
则 W×a+x×mg× =F·x,
∴ F=+=( -)2 +.
当且仅当 = 时,即
x= 时,力 F有最小值;
所以杠杆应当为 时,才能使得加在另一端用来平衡重物的力F最小。
习题 3.2
感受·理解
1. 证明下列不等式:
(1) a2+b2≥2a+2b-2;
证明:∵a2+1>2a,b2+1>2b,
∴ a2+b2+2≥2a+2b,
即 a2+b2≥2a+2b-2.
(2) ()2 ≤ ;
证明:∵ 2ab≤a2+b2,
∴ ()2=a2+2ab+b2≤=,
即 ()2 ≤ .
(3) 若 a,b ∈(0,+∞),则 ≤ .
证明:∵ a,b∈(0,+∞),
∴ 2≤a+b,
从而 ≤1,故 =≤.
2. 设 x>0,y>0,且 xy=4,求的最小值.
解:∵ x>0,y>0,xy=4,
∴ y=,∴ += + ≥2 =1,
当且仅当 = , xy=4,x>0,y>0.
即x=y=2 时取等号.
∴ + 的最小值是1.
3. 证明:
(1) x2+ ≥1;
证明:∵ x2+1>0,
∴ x2+=(x2+1)+-1
≥2-1=1,
即 x2+ ≥1. 当且仅当 x2+1= ,
即 x=0 时,取得等号.
(2) >2;
证明:∵==+
≥2 = 2,
当且仅当 = 时,等号成立.
∵ 对任意的实数x, ≠,∴ >2.
4. 求 1+2x2+ 的最小值.
解:1+2x2+ ≥1+2 =9
当且仅当 2x2= 即 x=±时等号成立.
∴ 1+2x2+ 的最小值为9.
5. 设 a,b 是正实数,求证:(a+)(b+)≥4.
解:∵ a>0,b>0,
∴ a+ ≥2 =2,
当且仅当 a=,即 a=1 时取等号.
∴ b+ ≥2 =2,
当且仅当 b =,即 b=1 时取等号.
∴ (a+)(b+) ≥2×2 =4,
当且仅当 a=b=1时取等号.
综上, (a+)(b+)≥4.
6. 如图,墙角线互相垂直,长为 a m 的木棒AB的两个端
点分别在这两墙角线上,如何放置木棒才能使围成区
域的面积最大
解:如图,设 AO=a m,BO=y m.
∵OA⊥OB
∴ OA2+OB2=AB2
∴ x2+y2=a2
∵(x-y)2≥0
∴ x2-2xy+y2≥0
∴ x2+y2≥2xy
∴ xy≤ (x2+y2), 即xy的最大值为 (x2+y2),
∵当 x=y 时, (x-y)2=0,
∴当 x=y 时, xy= (x2+y2),
即当 x=y 时,xy 的值最大,
∵ S△AOB=xy.
∴当 x=y 时,S△AOB面积最大,
由 x2+x2=a2 得 x=a
∴ 当OB=OA=a m 时,
木棒围成区域的面积最大.
7. 已知 a,b,c,d 都是正数,且 a<b,c<d,求证:
< .
证明:设点A(b,a),B(-c,-c),C(-d,-d),
∵a>0,b>0,c>0,d>0,
∴点A在第一象限,点B在第三象限,
点C第三象限,
且点B、点C都在直线 y=x上,
∵c<d,∴点B在点C的右上方,
∵a<b,∴点A在直线y=x (第一象限内)的下方,
在直角坐标系中表示出点A、点B、点C,
的几何意义是点A与点B连线的斜率,
的几何意义是点A与点C连线的斜率,
由图象可以看出直线AC的斜率更大,则 < .
思考·运用
8. 当 x≠0时,求 x+ 的取值范围.
解:当x>0时,x+ ≥2 =4,
∴当且仅当 x= 即 x=2 时等号成立;
当 x<0时, -x>0
∴ -x- ≥2 =4
∴ x+ ≤-4
∴当且仅当-x=- 即 x=-2 时等号成立,
∴ 综上所述, x+ 的取值范围为:
(-∞,-4)∪(4,+∞)
9. 如图,电路中电源的电动势为E,内阻为 r,R1为固定
电阻,R2是一个滑动变阻器. 已知 R2消耗的电功率为
P=()2R2. 当R2调至何值时, ()2R2
最大 最大值是多少
解:∵P=()2R2 =
=,
且 ≥2 =2;
∴P≤,当且仅当,
即 r+R1= R2时取等号,
∴当 r+R1= R2, P取得最大值,最大值是.
10. 某种产品的两种原料相继提价,产品生产者决定根
据这两种原料提价的百分比,对产品分两次提价,
现在有三种提价方案:
方案甲:第一次提价 p%,第二次提价 q%;
方案乙:第一次提价 q%,第二次提价 p%;
方案丙:第一次提价 %,第二次提价%.
其中p>q>0,比较上述三种方案,哪一种提价少
哪一种提价多
解:设提价前的价格为1,那么两次提价后的价格为,
方案甲:(1+p %)(1+q%)
=1+p%+q%+0.01pq%;
方案乙:(1+q%)(1+p%)
= 1+p%+q% +0.01pq%;
方案丙:(1+%) (1+%)
=1+p% +q% +(%)
=1+ p%+q% +0.01 ×()2%;
∵ ()2 ≥pq,且 p>q>0,
∴ 上式“=”不成立;
∴ 方案乙提价少,方案丙提价多.
探究·拓展
11. (阅读题)甲乙两同学分别解“设 x∈[0,+∞),求函
数 y=2x2+1的最小值”的过程如下:
甲:y=2x2+1≥2=2x,又x≥1,
所以2x>2 .
乙:因为y=2x2-1在区间[1,+∞)上的图象随着x增
大而逐渐上升,即y随x增大而增大,所以y的最
小值是 2×12+1=3.
试判断谁错,错在何处
解:甲的解法错误,乙的解法正确.
甲同学的解法:利用基本不等式法求最小值,
∵ 2x2+1 ≥ 2 = 2,但由于2x,不是定值,
且未考虑取等的问题,所以解法错误.
乙同学的解法:
∵ y=2x2+1在[1,+∞) 上单调递增,
∴ y=2x2+1的最小值是 2×12+1=3,解法正确.
综上所述:甲同学的解析错误,基本不等式应用错误.
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
