3.3 从函数观点看一元二次方程和一元二次不等式 课件(共133张PPT)
文档属性
| 名称 | 3.3 从函数观点看一元二次方程和一元二次不等式 课件(共133张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 63.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 00:00:00 | ||
图片预览









文档简介
(共133张PPT)
第3章 不等式
3 . 3
从函数观点看一元二次方程和一元二次不等式
我们知道,一次函数、一元一次方程、一元一次不等式之间有着密切的联系. 例如,可以借助函数 y=2x-3 的图象来求解 2x-3=0,2x-3>0,2x-3<0.
反过来,也可以通过求解 2x-3=0,2x-3>0,
2x-3<0,来深人理解函数 y=2x-3的性质,那么
●怎样从函数观点进一步解决方程、不等式的问题
3. 3 . 1
从函数观点看一元二次方程
从函数的观点看,方程 x2-2x-3=0的两个根 x1=-1,x2=3,就是二次函数 y=x2-2x-3 当函数值取零时自变量x的值,即二次函数 y=x2-2x-3 的图象与x轴交点的横坐标.
这时,我们称-1,3 为二次函数 y=x2-2x-3 的零点.
一、二次函数的零点
一般地,一元二次方程 ax2+bx+c=0 (a≠0) 的根就是二次函数 y=ax2+bx+c (a≠0) 当函数值取零时_______________,即二次函数 y=ax2+bx+c (a≠0) 的图象与______________________,也称为二次函数 y=ax2 +bx+c (a≠0)的零点.
自变量x的值
x轴交点的横坐标
【思考】
二次函数的零点就是二次函数图象与x轴的交点吗
提示:不是,二次函数的零点是二次函数图象与x轴交点的横坐标.
二、一元二次方程 ax2+bx+c=0(a≠0)的根、
二次函数 y=ax2+bx+c(a≠0)的图象、
二次函数y=ax2+bx+c(a≠0)的零点之间的关系.
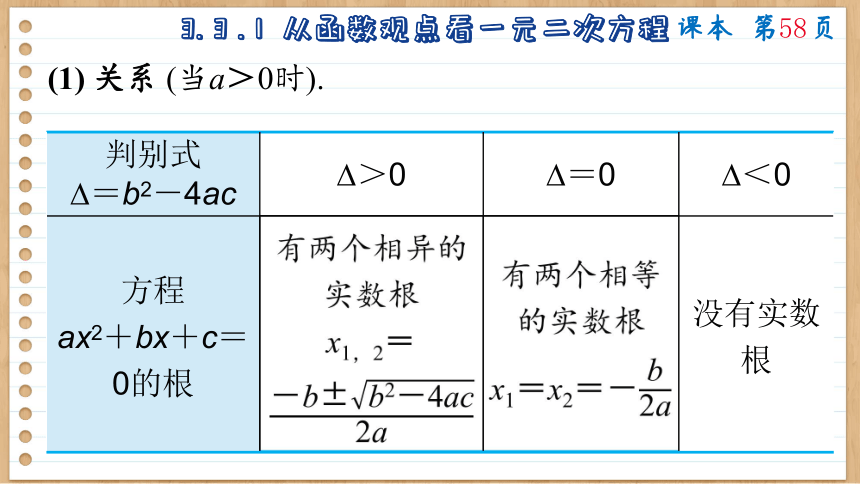
(1) 关系 (当a>0时).
判别式 =b2-4ac >0 =0 <0
方程 ax2+bx+c=0的根 有两个相异的实数根 x1,2= 有两个相等的实数根 x1=x2=- 没有实数根
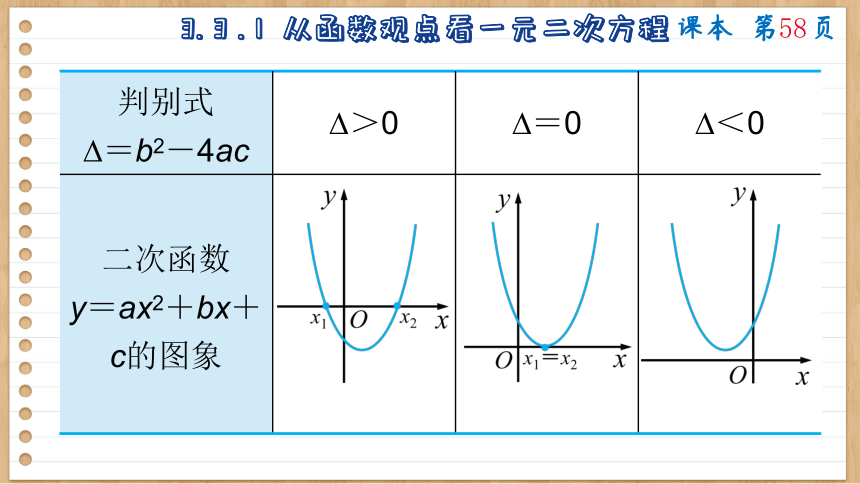
判别式 =b2-4ac >0 =0 <0
二次函数 y=ax2+bx+c的图象
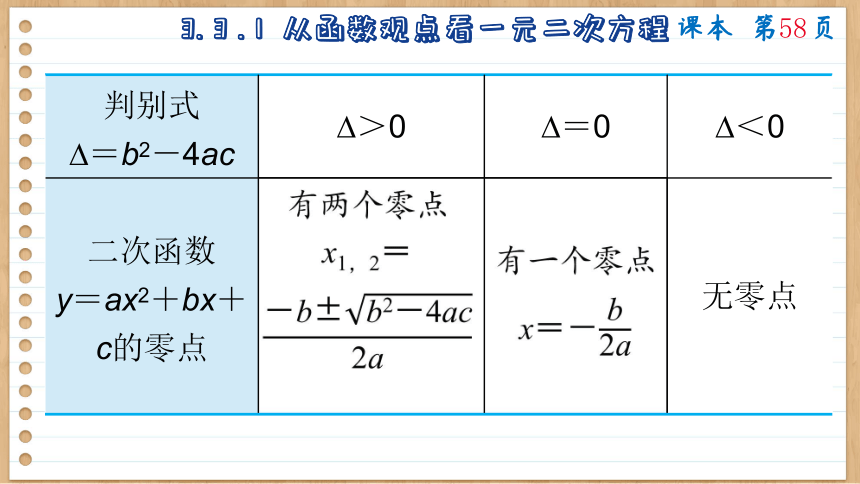
判别式 =b2-4ac >0 =0 <0
二次函数 y=ax2+bx+c的零点 有两个零点 x1,2= 有一个零点x=- 无零点
当a<0时,一元二次方程 ax2+ba+c=0 的根次函数 y=ax2+bx+c 的图象次函数 y=ax2+bx+c 的零点之间的关系请同学们自行完成(见练习 1).
(2) 本质:
判别式 Δ>0,Δ=0,Δ<0的情况决定着一元二次方程根、二次函数图象与x轴交点和二次函数零点的情况.
(3)应用:①求二次函数的零点;
②证明二次函数零点的个数;
③判断二次函数零点所在的区间.
例 1
求证:二次函数 y=2x2+3x-7 有两个零点.
分析 要证明二次函数 y=x2+3x-7 有两个零点,只需证明元二次方程 2x2+3x-7=0有两个不相等的实数根即可.
证明:考察一元二次方程 2x2+3x-7=0.
因为 =32-4×2×(-7) =65>0,
所以方程 2x2+3x-7=0 有两个不相等的实数根.
因此,二次函数 y=2x2+3x-7有两个零点.
例 2
判断二次函数 y=x2-2x-1在区间(2,3)上是否存在零点.
解:根据求根公式可得一元二次方程 x2-2x-1=0 的两个根分别为 x1=1+,x2=1-.
因为 1< <2,
所以 1<1+< 3.
因此,二次函数y=x2-2x-1在区间(2,3)上存在零点.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) a>0时二次函数 y=ax2+bx+c有两个零点.( )
(2) 如果二次函数 y=ax2+bx+c与x轴没有交点,则此二次函数没有零点. ( )
Δ>0时二次函数 y=ax2+bx+c有两个零点.
2. 二次函数 y=ax2+bx+c (a≠0)中若 b2>4ac,则函数
零点的个数为 ( )
A. 0 B. 1 C. 2 D. 不能确定
C
解析:因为b2>4ac,
所以 Δ=b2-4ac>0,
所以 函数有2个零点.
解析
3. 函数 y=(x+2)(x+1) 的零点是_____________.
-2,-1
解析:令(x+2)(x+1)=0,
解得 x=-2或 x=-1,
所以函数的零点是-2, -1.
解析
【跟踪训练】
1. 若 b2-4ac=0,则二次函数 y=ax2+bx+c (a≠0) 零点的个数为 ( )
A. 0个 B.1个 C.2个 D.无法确定
B
解析:因为 b2-4ac=0,
所以一元二次方程 ax2+bx+c=0有两个相等的实数根,
所以二次函数 y=ax2+bx+c 有一个零点.
解析
2. 二次函数 y= (2x+1)(x-5)的零点为 ( )
A. ,-5 B. - ,5
C. 2,- D. -2,
B
解析:因为方程 (2x+1)(x-5)=0 的两个根为x1=-,x2=5,
所以二次函数 y=(2x+1)(x-5) 的零点为- ,5.
解析
3. 二次函数 y=x2-2的零点所在的区间为 ( )
A. (1,0) B. (1,2) C.(2,3) D.(3,4)
B
解析:解方程 x2-2=0得,x=±,
其中1<<2.
解析
4. 已知二次函数的图象如图所示,则此函数的零点为
____________.
-1,1
解析:因为二次函数的图象与x轴交点的横坐标分别为- 1,1,
所以此函数的零点为-1,1.
解析
5. 二次函数 y=x2-ax 的一个零点为2,则a=________.
解析:由题意,x=2是方程x2-ax=0的根,
所以 4-2a=0,解得 a=2.
解析
2
练 习
1. 当 a < 0 时,请填下表:
判别式 =b2-4ac >0 =0 <0
方程 ax2+bx+c=0的根 有两个相异的实数根 x1,2= 有两个相等的实数根 x1=x2=- 没有实数根
判别式 =b2-4ac >0 =0 <0
二次函数 y=ax2+bx+c的图象
判别式 =b2-4ac >0 =0 <0
二次函数 y=ax2+bx+c的零点 有两个零点 x1,2= 有一个零点x=- 无零点
2. 画出二次函数 y=x2-x-2 的图象,并指出该函数
的零点.
解:二次函数 y=x2-x-2 图象如下:
由 x2-x-2=0 得,
x=-1或x=2.
故所求零点为-1,2.
3. 求下列二次函数的零点:
(1) y=(x+1)(x-1);
(2) y=x2-4x;
解:令 y=0,得x1=-l,x2=1,
所以函数的零点为-1和 1.
解:令 y=0,即 x2-4x=0,得x(x-4)=0,
解得x1=0,x2=4,
所以函数的零点为 0 和 4 .
(3) y=-3x2-9;
(4) y=-x2+2x-1.
解:令 y=-3x2-9=0,方程无实数根,
所以函数无零点.
解:令 y=-x2+2x-1=0,即x2-2x+1=0,
得 (x-1)2=0,解得 x=1.
所以函数的零点为1.
3. 3 . 2
从函数观点看一元二次不等式
我们来看下面的问题:
某杂志以每册 2 元的价格发行时,发行量为 10 万册经过调查若单册价格每提高 0.2 元,则发行量就减少 5000 册要使杂志社的销售收入大于 22.4 万元,每册杂志的价格应定在怎样的范围内
设每册杂志价格提高 x 元,则发行量减少
0.5×=
万册,杂志社的销售收人为(2+x)(10-)万元.
根据题意,得 (2+x)(10-) >22.4,
化简,得 5x2-10x+4.8 < 0.
一、一元二次不等式的概念
只含有一个未知数,并且未知数最高次数是 2 的_______________叫作一元二次不等式.
整式不等式
【思考】
不等式 x2+ > 0是一元二次不等式吗
提示:不是,一元二次不等式一定是整式不等式.
我们知道,一元二次方程和相应的二次函数有着密切的联系,一元二次方程的根就是相应二次函数的图象与x轴交点的横坐标.
那么,
● 一元二次不等式和相应的二次函数是否也有内在的联系
二、一元二次不等式和相应的二次函数的对应关系
(1) 关系:(a>0)
判别式 =b2-4ac >0 =0 <0
方程 ax2+bx+c=0的根 有两个相异的实数根 x1,x2 (x1<x2) 有两个相等的实数根 x1=x2=- 没有实数根
判别式 =b2-4ac >0 =0 <0
二次函数 y=ax2+bx+c的图象
判别式 =b2-4ac >0 =0 <0
ax2+bx+c>0的解集 (-∞,x1) ∪ (x2,+∞) (-∞,-) ∪ (-,+∞) R
ax2+bx+c<0的解集 (x1<x2)
【思考】
(1) 有人说:当 Δ>0 时表中的 x1,x2 有三重身份,
你能说出是哪三重身份吗
提示:x1,x2 既是二次函数图象与x轴交点的横坐标 (即二次函数的零点),又是一元二次方程的两个解,还是一元二次不等式解集的区间端点.
(2) 若一元二次不等式 ax2+x-1>0 (a≠0) 的解集为R,
则实数 a 应满足什么条件
提示:结合二次函数图象可知,若一元二次不等式 ax2+x-1>0 (a≠0)的解集为R,
则 解得 a∈ ,
所以不存在a使不等式 ax2+x-1>0 的解集为R.
a>0
1+4a<0
(2) 本质:
方程 ax2+bx+c=0 (a≠0) 和不等式 ax2+bx+c>0
(a>0) 或 ax2+bx+c<0 (a>0) 是函数 y=ax2+bx+c
(a≠0) 的特殊情况,它们之间是一种包含关系,也就是当 y=0 时,函数 y=ax2+bx+c (a≠0) 就转化为方程,当 y>0 或 y<0 时就转化为一元二次不等式.
(3) 应用:
① 解一元二次不等式,
② 已知一元二次不等式的解集求参数,
③ 一元二次不等式的应用问题.
当a<0 时,通过不等式两边同乘以-1,可将问题转化为二次项系数为正的情形,利用表3-3-2解决.
例 1
解下列不等式:
(1) x2-7x+12>0;
(2) -x2-2x+3≥0;
(3) x2-2x+1<0;
(4) x2-2x+2>0.
(1) x2-7x+12>0;
解 方程 x2-7x+12=0 的解为 x1=3,x2=4.
根据 y=x2-7x+12 的图象
可得原不等式的{ x∣x<3 或 x>4}.
(2) -x2-2x+3≥0;
对 于二次项系数为负数的不等式,可以先把二次项系数化成正数,然后再求解.
解 不等式两边同乘以-1,得 x2+2x-3≤0.
方程 x2+2x-3=0 的解为 x1=-3,x2=1.
根据 y = x2+2x-3 的图象,
可得原不等式的解集为 { x∣-3≤x≤1).
(3) x2-2x+1<0;
解 方程 x2-2x+1=0 有两个相同的解x1=x2=1.
根据 y=x2-2x+1的图象,
可得原不等式的解集为 .
(4) x2-2x+2>0.
解 因为 <0,所以方程 x2-2x+2=0 无实数解.
根据 y=x2-2x+2 的图象,
可得原不等式的解集为 R .
练 习
1. (1) 不等式(x-1)(x-3)>0的解集为( )。
A.{ x∣x<1} B.{ x∣x>3}
C.{ x∣x<1 或 x>3} D.{ x∣1<x<3}
(2) 不等式-x2+2x-4>0 的解集为( ).
A. R B.
C. { x∣x>0,x∈R} D.{ x∣x<0,x∈R}.
C
B
2. 解下列不等式:
(1) x2+4x-12>0;
解:该不等式可化为(x+6)(x-2)>0,
解得 x<-6或 x>2,
故原不等式的解集为{ x∣x<-6 或 x>2}.
(2) x2-x+1≤0;
解:该不等式可化为(x-)2+≤0 ,
无解,
故原不等式的解集为 .
(3) 2x2-5x+3<0;
解:该不等式可化为(x-1)(2x-3) <0,
解得 1<x< ,
故原不等式的解集为{ x∣ 1<x< }.
(4) 3x2-x-4>0;
解:该不等式可化为(x+1)(3x-4) >0,
解得 x<-1或 x> ,
故原不等式的解集为{ x∣ x<-1或 x> }.
(5) 2x2+4x+3>0;
解:该不等式可化为2(x+1)2+1>0,
恒成立,
故原不等式的解集为R.
(6) 9x2-6x+1≤0.
解:该不等式可化为(3x-1)2 ≤0,
解得 x=,
故原不等式的解集为{ x∣ x= }.
3. 解下列不等式:
(1) -6x2-x+2<0;
解:不等式可变形为 6x2+x-2>0 ,
对应方程的两根分别为和-,
由 y=6x2+x-2的图象知解集为
{ x∣x <- 或 x> }
(2) 1-4x2≥4x+2;
解:不等式可变形为4x2+4x+1<0,
即(2x+1)2<0,
显然无解,
即解集为 .
(3) 1-3x<x2;
解:不等式可变形为 x2+3x-1>0,
对应方程的两根为 x1,2== ,
由 y=x2+3x-1的图象知解集为
{ x∣x < 或 x > }.
(4) (x-2)(x+2) >1.
解:不等式可变形为 x2-5>0,
对应方程的两根为 x1=-,x2=,
由 y=x2-5 的图象知解集为
{ x∣x<- 或 x> }.
4. 当 x 是什么实数时,函数 y=-x2+5x+14 的值是:
(1) 0
解: -x2+5x+14=0
x2-5x-14=0
(x-7)(x+2) =0
x1=7,x2=-2
(2) 正数
解: -x2+5x+14>0
x2-5x-14<0
(x-7)(x+2) <0
-2<x<7
(3) 负数
解: -x2+5x+14<0
x2-5x-14>0
(x-7)(x+2) >0
x>7 或 x<-2.
5. (1)已知集合 M={x|-4≤x≤7,N={x|x2-x-6>0},
求M∩N;
解:∵集合M = {x∣-4≤x≤7},
N = {x|x2-x-6>0}
= {x∣x<-2或 x>3},
∴ M∩N ={x∣-4≤x<-2 或 3< x≤7};
(2) 已知集合 A={x|x2-4x+3<0},B={x|(x-2)(x-5)
<0},求 A∪B.
解:∵集合A={x|x2-4x+3<0}
={x∣1<x<3},
B={x|(x-2)(x-5)<0}
={x∣2<x<5},
∴ A∪B ={x∣1<x<5}.
例 2
用一根长为 100 m的绳子能围成一个面积大于 600 m的矩形吗 当长、宽分别为多少米时,所围成的矩形的面积最大
解:设矩形一边的长为 x m,则另一边的长为 (50-x) m,其中0<x<50.
由题意,得 x(50-x) >600,
即 x2-50x+600<0,
解得 20<x<30.
所以,当矩形一边的长在 20 m 至 30 m 的范围内取值时,能围成一个面积大于 600 m2 的矩形.
用 S 表示矩形的面积,则
S=x(50-x)
=- (x-25)2+625 (0<x<50).
当x=25 时,S 取得最大值,此时 50-x=25.
答 当矩形的长、宽都为25m时,所围成的矩形的面积最大.
你能用基本不等式来求 x(50-x) 的最大值吗
例 3
某小型服装厂生产一种风衣,日销货量 x 件(x∈N*)与货价 P 元/件之间的关系为 P=160-2x,生产 x 件所需成本为 C=500+30x 元.
问:该厂日产量多大时,日获利不少于1300 元
解 由题意,得 (160-2x)x-(500+30x)>1300,
化简,得 x2-65x+900<0,
解得 20≤x≤45.
答 该厂日产量在20件至45件时,日获利不少于1300元.
例 4
汽车在行驶中,由于惯性的作用,刹车后还要继续向前滑行一段距离才能停住,我们称这段距离为“刹车距离”刹车距离是分析事故产生原因的一个重要因素.
在一个限速为 40 km/h的弯道上,甲乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相碰.
事后现场勘查测得甲车的刹车距离小于 12 m,乙车的刹车距离略超过 10 m. 又知甲两种车型的刹车距离 (单位:m)与车速 x (单位:km/h)之间分别有如下关系:
s甲= 0.1x+ 0.01x, s乙=0.05x+0.005x2.
问:甲、乙两车有无超速现象
一般来说,刹车距离与车速是二次函数关系.
分析 根据汽车的刹车距离可以估计汽车的车速.
解 由题意知,对于甲车,有 0.1x+0.01x2<12,
即 x2+10x-1200<0,
解得 -40<x<30.
这表明甲车的车速低于 30 km/h,未超过规定限速.
对于乙车,有 0.05x+0.005x2>10,
即 x2+10x-2000>0,
解得 x>40 或 x<-50 (不合实际意义,舍去).
这表明乙车的车速超过 40 km/h,超过规定限速.
答 甲车未超过规定限速,乙车超过规定限速.
练 习
1. 如果某厂扩建后计划后年的产量不低于今年的 2倍,
那么明、后两年每年的平均增长率至少是多少
解:设该厂今的产量为a,明、后两年每年的平均增长率至少是x%,则a(1+x%)2≥2a,
解得 x%≥41.4%.
∴ 明、后两年每年的平均增长率至少是41.4%.
2. 销售某种商品,单价为 a 元时,销售量是b. 经市场调
研可以预测,若单价上涨 m%,则销售量将减少.
为了使该商品的销售金额最大,m 应定为多少
解:设原来销售金额为y,
根据题意可知调整后的单价是a·(1+),
售出的数量是 b·(1-),
调整后的销售金额为:
y=a·b·(1+)(1-) =a·b·(1-m2+m)
= - m2 + m +
=[-(m-25)2 +]ab
∵ab均为正,
∴当m=25时,y最大,
故m定为25.
3. 国家为了加强对饮用酒生产的宏观管理,实行征收附
加税政策.已知某种洒每瓶 70 元,不征收附加税时,
每年大约销售 100 万瓶;若政府征收附加税每销售
100 元要征税 R元 (叫作税率 R%),则每年的销售量
将减少 10R 万瓶. 要使每年在此项经营中所收取的附
加税不少于 112 万元,R 应怎样确定
解:设产销量为每年x万瓶,则销售收入为每年70x万元,从中征收的税金为 70x·R%万元,其中 x=100-10R.
由70(100 - 10R)·R%≥112,
即 R2-10R+16 < 0.
解得 2≤R≤8.
故税率定在2% ~ 8%之内,年收附加税额将不低于112万元.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) mx2-5x<0 是一元二次不等式 ( )
(2) 若 a>0,则一元二次不等式 ax2+1>0无解( )
当m=0时是一元一次不等式;
当m≠0时,它是一元二次不等式.
因为a>0,所以不等式ax2+1>0恒成立,即原不等式的解集为R.
(3) 若一元二次方程 ax2+bx+c=0(a≠0) 的两根为x1,x2 (x1<x2),则一元二次不等式 ax2+bx+c<0的解集为{ x∣x1<x<x2 }. ( )
当 a>0时,ax2+bx+c<0的解集为{ x∣x1<x<x2},否则不成立.
2. 不等式 (2x+1)(x-1)>0 的解集是 ( )
A. { x∣-<x<1} B.{ x∣x>1}
C.{ x∣x<1 或 x>2} D. { x∣x<-或 x>1}
D
解析:因为方程 (2x+1)(x-1)=0的解为 x1=-,x2=1,
所以根据函数 y=(2x+1)(x-1)的图象,可得原不等式的解集为{ x∣x<-或 x>1} .
解析
3. 不等式-3x2+5x-4>0 的解集为________.
解析:原不等式变形为 3x2-5x+4<0.
因为Δ= (-5)2-4×3×4=-23<0,
所以由函数 y=3x2-5x+4 的图象可知,
3x2-5x+4<0 的解集为 .
解析
【跟踪训练】
1. 不等式 (-x)(-x)>0 的解集是 ( )
A.{ x∣ <x<}
B. { x∣x> }
C. { x∣x<}
D.{ x∣x<或x> }
D
解析:方程(-x)(-x) =0的两根为 x1=,x2=,所以原不等式的解集为{ x∣x<或x> }.
解析
2.一元二次不等式ax2+bx+2>0(a≠0)的解集是(-, ),
则a+b的值是( )
A.10 B. -10 C.14 D. -14
D
解析:方程ax2+bx+2=0(a≠0)的两个根为-和 ,
-+= - ,-×= ,
所以 a=-12,b=-2,a+b=-14.
解析
3. 某公司每个月的利润 y (单位:万元)关于月份 n 的关
系式为 y=n2-9n+114,则该公司12个月中,利润大
于100万元的月份共有 ( )
A. 4个 B. 5个 C. 6个 D. 7个
C
解析:由题意得 n2-9n+114>100,
解得 n<2或 n>7,
故 n=1,8,9,10,11,12,共6个月.
解析
4. 二次函数 y=x2-4x+3当函数值为负数时 x 的取值范
围是___________.
1<x<3
解析:由于方程 x2-4x+3=0 的两个根为 x1=1,x2=3.
故不等式 x2-4x+3<0 的解集为{ x∣1<x<3}.
解析
5. 不等式-x2+mx+m<0 恒成立的条件是__________.
-4<m<0
解析:-x2+mx+m<0 恒成立,等价于Δ<0,
即 m2+4m<0,
所以-4<m<0.
解析
习题 3.3
感受·理解
1. 证明:函数 y=x2-x+1 没有零点.
解:∵ = b2-4ac
= (-1)2-4×1×1
=1-4 =-3 <0.
∴ 函数 y=x2-x+1没有零点.
2. 设 m 为实数,若函数 y= x2-mx+2 有只有一个零点,
求 m 的值.
解:函数 y=x2-mx2 有且只有一个零点,
一个根,则 =m2-8=0,
所以 m ±2.
3. 设k为实数,若方程 x2-3x+k-3=0 有实数根,求 k
的取值范围.
解:将方程整理得:4x2-12x+k-3=0,有题意知:
=122-4×4×(k-3)<0,
解得:k>12.
∴ k 取值范围是(12,+∞).
故答案为:(12,+∞)
4. 证明:函数 y=5x2-7x-1的一个零点在区间(-1,0)
内,另一个零点在区间(1,2)内.
解:令f(x)=5x2-7x-1,则f(x)在R上是连续函数.
∵ =(-7)2-4×5-(-1) =49+20=69>0,
∴方程 f(x)=0 有两个不等实数根,
即f(x) =5x2-7x-1在R上有两个零点;
又∵f(-1)=5×(-1)2-7×(-1) -1=11>0,
f(0)= -1<0,
∴ 在区间(-1,0)内,函数f(x)=5x2-7x-1存在零点;
又∵ f(1) = 5-7-1=-3<0,
f(2) = 5×22-7×2-1=5>0,
∴在区间(1,2)内,函数f(x)=5x2-7x-1存在零点.
又∵函数f(x)=5x2-7x-1在R上有且仅有两个零点,
∴ 函数f(x)=5x2-7x-1一个零点在区间(-1,0)内,
另一个零点在区间(1,2)内.
5. 解下列不等式:
(1) x(x-1) ≤ 0;
(2) (x+1)(x-5)>0;
解:因为对应方程的两根为0和1,
所以不等式的解集是{x∣0≤x≤1}.
解:因为对应方程的两根为-1和5,
所以不等式的解集是{x∣x<-1或x>5}.
(3) x2-6x+9≤0;
(4) 3x2-7x+2 > 0;
解:因为对应方程为(x-3)2=0,
对应方程的一个根为3,
所以不等式的解集是{x∣x=3}.
解:因为对应方程的两根为2和,
所以不等式的解集为{ x∣x<或x>2}
(5) -2x2-x+6>0;
(6) x2-x+1>0.
解:因为不等式可化为 2x2+x-6≤0,
对应方程的两根为-2和,
所以不等式的解集为{ x∣-2≤ x≤ }.
解:因为对应方程判别式 <0,
所以不等式的解集为R.
6. 解下列不等式:
(1) 2x2-3x>2;
解:∵ 2x2-3x-2>0,
∴ (2x+1)(x-2)>0,
∴x<-或x>2,
∴不等式的解集为{x∣x<-或x>2}.
(2) 3x2-5x+4>0;
解:∵ =25-4×3×4
=-23<0,
∴不等式3x2-5x+4>0的解集为R.
(3) x(x+2) <x(3-x) +1;
解:∵原不等式可化为:2x2-x-1<0,
即(2x-1)(x-1) <0,
∴-<x<1,
∴不等式的解集为{x∣-<x<1}.
(4) (3x-1) (x+1)>4.
解:∵原不等式可化为:3x2+2x-5<0,
即(3x+5)(x-1)>0,
∴ x<- 或 x>1,
∴不等式的解集为:{x∣ x<- 或 x>1}.
7. 当x是什么实数时,函数 y=-x2-8x+20 的值是:
(1) 0
解:-x2-8x+20 =0
x2+8x-20 =0
(x-2)(x+10) =0
x=-10或x=2
(2)正数
解:-x2-8x+20 >0
x2+8x-20 <0
(x-2)(x+10) <0
-10<x<2
(3)负数
解:-x2-8x+20 <0
x2+8x-20 >0
(x-2)(x+10) >0
x<-10 或 x>2
8. 制作一个高为 20 cm 的长方体容器,底面矩形的长比
宽多 10 cm,并且容积不少于 4 000 cm3.
问:底面矩形的宽至少应是多少
解:设底面矩形的宽为 x cm,
由题意可得20x(x+10) ≥ 4000.
即 x2+10x-200≥0,
解得:x≤-20 (舍) 或x≥10.
∴ 底面矩形的宽至少应为10 cm.
9. 已知二次函数y=x2+bx+c的图象与x轴交于A(-1,0),
B(2,0)两点,求关于x的不等式 x2+bx+c>0 的解集.
解:∵ 二次函数 y=x2+bx+c 的图象与x轴交于
A(-1,0),B(2,0) 两点,
∴ -1,2 是关于x的一元二次方程 x2+bx+c=0
的两个实数根,
∴关于x的不等式x2+bx+c>0 的解集为:
{x∣x<-1或x>2}.
思考·运用
10. 设m为实数已知二次函数 y=x2-5x+m 的两个零点都
在区间(0,+∞)内,求 m 的取值范围.
解:二次函数 y=x2-5x+m的图象是一条抛物线,
开口向上,对称轴方程为 x=,
若它的两个零点都在区间(1,+oo)内,
只需满足 =(-5)2-4×1·m>0
f(1)=-4+m>0
解得:4<m<,
∴ m 的取值范围是(4, )
11. (1) k 是什么实数时,方程 x2+2(k-1)x+3k2-11=0
有两个不相等的实数根
解:方程 x2+2(k-1)x+3k2-11=0中,
令 >0,得 4(k-1)2-4(3k2-11)>0,
化简得 k2+k-6<0,
解得 -3<k<2,
所以 k∈(-3,2) 时,方程有两个不相等的实数根;
(2) 已知不等式 x2-2x+k2-1>0 对一切实数 x 恒成立,
求实数k的取值范围.
解:不等式 x2-2x+k2-1>0 对一切实数x恒成立,
∴ <0,即4-4(k2-1) <0,
化简得 k2>2,
解得 k> 或 k<-;
∴实数k的取值范围是(-∞,-)∪(+∞).
12. 已知不等式 ax2+b-1>0的解集是{ x∣3<x<4 },
求实数 a,b 的值.
解:由题意知,a<0,
且 3,4 是方程 ax2+bx-1=0的根.
∴
解得
9a+3b-1=0
16a+4b-1=0
a=-
b=
13. 如图,某房地产开发公司要在矩形地块 ABCD 上规划出一块矩形地块PQCR 建造住宅区为了保护文物,住宅区不能超越文物保护区△AEF的界线EF. 由实地测量知,AB=200 m,AD=160 m,
AE =60 m,AF=40 m.
问:怎样设计矩形住宅区的长和宽,
才能使其面积最大 最大面积是多少
G
解:设PQ交DA于点G,如图所示:
设PQ=x,140≤x≤200,
则GP=200-x,
∵△GPF~△AEF,
∴ FG= (200-x)
∴ PR=DF+FG=120+ (200-x),
∴ SPQCR =x[120+ (200-x)]=-x2+x
=-(x-190)2+,
当x=190 时,即 PR=120+120+(200-190)=时,
SPQCR取得最大值,
故当矩形住宅区的长为190m,宽为m时, SPQCR取得最大值m2.
14. 已知某公司每天生产的某种产品的数量 (单位:百件)
与其成本y (单位:千元)之间的函数解析式可以近似
地用 y=ax2+b+c 表示其中a,b,为常数. 现有实际
统计数据如下表所示:
产品数量x/百件 6 10 20
成本y/千元 104 160 370
产品数量x/百件 6 10 20
成本y/千元 104 160 370
(1) 求a,b,c 的值;
解:将表格中相关数据代入 y=ax2+bx+c.
36a+6b+c=104
得 100a+10b+c=160,
400a+20b+c=370
解得 a=,b=6,c=50.
(2) 若每件产品销售价为 200 元,则该公司每天生产多少
产品时才能盈利 (假设每天生产的产品可以全部售完)
解:由(1)知,y= x2+6x+50(x≥0),
由题意可知 200x×0.1-y>0
即 -x2+14x-50 >0,
解得 4.2< x <23.8
故该公司每天生产产品数量在区间(420,2380)时才能盈利.
探究·拓展
15. (阅读题)重新考察不等式 5x2-10x+4.8<0 这个不等
式的左边可分解因式为(x-1.2)(5x-4). 根据实数乘
法的符号法则,问题可归结为求一元一次不等式组
的两个解集的并集.
x-1.2<0, x-1.2>0.
(1) 和 (2)
5x-4>0 5x-4<0
不等式组(1)的解为 0.8<x<1.2 不等式组(2)无解,从而不等式 5x2-10x+4.8<0 的解集为{ x∣0.8<x<1.2}.
试用上述方法解下面的不等式:
(1) (2x-3)(x+1) >0; (2) (1-x)(2+x)≥0;
(3) <0; (4) ≤0.
(1) (2x-3)(x+1) >0;
解:∵ (2x-3)(x+1)>0,
∴ ,或
解得 x>,或 x<-1,
∴ 原不等式的解集为{x∣ x<-1或x>};
2x-3>0
x+1>0
2x-3<0
x+1<0
(2) (1-x)(2+x)≥0;
解:∵ (1-x)(2+x)≥0,
∴ ,或
解得 -2≤x≤1,或 无解,
∴ 原不等式的解集为{x∣ -2≤x≤1};
1-x≥0
2+x≥0
1-x≤0
2+x≤0
(3) <0;
解:∵ <0 ,
∴ ,或
解得 -3<x<1 ,或无解,
∴ 原不等式的解集为{x∣ -3<x<1 };
x-1<0
x+3>0
x-1 > 0
x+3<0
(4) ≤0.
解:∵ ≤0 ,
∴ ,或
解得 x≥,或 x<-4,
∴ 原不等式的解集为{x∣ x<-4或x≥};
1-2x ≤ 0
x+4>0
1-2x ≥ 0
x+4 < 0
问题与探究
基本不等式的推广
我们已知基本不等式 ≤ (a,b > 0),那么,对于3个正数 a,b,c,是否有
≤
对于4个正数a,b,c,d,是否有
≤
给出一些具体数,借助计算机(器)验证一下,并尝试给出证明. 你还会有什么猜想
阅 读
不等号的演变
在早期,人们使用文字或象征性记号来记述不等关系.例如,荷兰数学家吉拉尔 ( A . Girard,1595—1632) 在他 1629 年所著《代数新发现》一书中,使用下面记号:
A ff B 表示A大于B,B§A 表示B小于A.
1631年,英国数学家奥特雷德 ( W . Oughtred,1574—1660) 在《数学入门》一书中,用符号:
表示大于, 表示小于.
也有传说,用符号:
表示大于, 表示小于.
1634 年,法国数学家厄里岗( P.Herigone ) 在《数学教程》一书中,采用符号:
a3I2b 表示a大于b,b2I3a 表示a小于b.
他的意思是说,因为 3>2,所以 a3>2b ( a,b 为正数),故 a>b,小于号的意思也是这样的.
1631年,英国数学家、望远镜发明者哈里奥特 ( T . Harriot,1560-1621)去世后 10 周年,人们出版了他的遗著《分析术实例》在这本书中,他写道:
大于的记号:a>b表示 a 量大于 b 量,
小于的记号:a<b表示 a 量小于 b 量.
这一简洁优美的记号,不管后人采用怎样的方式去创造不等号最终都无法取代“>”“<”两个记号.“>” “<”直到 18 世纪初才被泛使用.
至于“≠”“≯”“≮”的出现,乃是近代之事. 一般人不使用“≮”“≯”,而使用“≥”“≤”(或“≧”“≦”)两个记号,表示“大于或等于”“小于或等于”.
在数学史上,也有数学家使用“”表示“等于或大于”,“”表示“等于或小于”.
在少数数学著作中,也出现用“∨”表示小于,“∧”表示大于.例如,2∨3表示“2 小于 3”,9∧7表示“9 大于7”,这种写法没有得到广泛传播,更多的数学书只将符号“∨”表示“<”“>”“≤”“≥”中的一种.例如,a∨b表示“a>b”“a<b”“a≥b”“a≤b”中的一种.
高等数学中,还出现“”表示“远小于”,“”表示“远大于”.
在有些计算机语言中,使用“<>”表示“不等于”,“>=”表示“大于或等于”,“<=”表示“小于或等于”.
本课结束
This lesson is over
THANKS!
第3章 不等式
3 . 3
从函数观点看一元二次方程和一元二次不等式
我们知道,一次函数、一元一次方程、一元一次不等式之间有着密切的联系. 例如,可以借助函数 y=2x-3 的图象来求解 2x-3=0,2x-3>0,2x-3<0.
反过来,也可以通过求解 2x-3=0,2x-3>0,
2x-3<0,来深人理解函数 y=2x-3的性质,那么
●怎样从函数观点进一步解决方程、不等式的问题
3. 3 . 1
从函数观点看一元二次方程
从函数的观点看,方程 x2-2x-3=0的两个根 x1=-1,x2=3,就是二次函数 y=x2-2x-3 当函数值取零时自变量x的值,即二次函数 y=x2-2x-3 的图象与x轴交点的横坐标.
这时,我们称-1,3 为二次函数 y=x2-2x-3 的零点.
一、二次函数的零点
一般地,一元二次方程 ax2+bx+c=0 (a≠0) 的根就是二次函数 y=ax2+bx+c (a≠0) 当函数值取零时_______________,即二次函数 y=ax2+bx+c (a≠0) 的图象与______________________,也称为二次函数 y=ax2 +bx+c (a≠0)的零点.
自变量x的值
x轴交点的横坐标
【思考】
二次函数的零点就是二次函数图象与x轴的交点吗
提示:不是,二次函数的零点是二次函数图象与x轴交点的横坐标.
二、一元二次方程 ax2+bx+c=0(a≠0)的根、
二次函数 y=ax2+bx+c(a≠0)的图象、
二次函数y=ax2+bx+c(a≠0)的零点之间的关系.
(1) 关系 (当a>0时).
判别式 =b2-4ac >0 =0 <0
方程 ax2+bx+c=0的根 有两个相异的实数根 x1,2= 有两个相等的实数根 x1=x2=- 没有实数根
判别式 =b2-4ac >0 =0 <0
二次函数 y=ax2+bx+c的图象
判别式 =b2-4ac >0 =0 <0
二次函数 y=ax2+bx+c的零点 有两个零点 x1,2= 有一个零点x=- 无零点
当a<0时,一元二次方程 ax2+ba+c=0 的根次函数 y=ax2+bx+c 的图象次函数 y=ax2+bx+c 的零点之间的关系请同学们自行完成(见练习 1).
(2) 本质:
判别式 Δ>0,Δ=0,Δ<0的情况决定着一元二次方程根、二次函数图象与x轴交点和二次函数零点的情况.
(3)应用:①求二次函数的零点;
②证明二次函数零点的个数;
③判断二次函数零点所在的区间.
例 1
求证:二次函数 y=2x2+3x-7 有两个零点.
分析 要证明二次函数 y=x2+3x-7 有两个零点,只需证明元二次方程 2x2+3x-7=0有两个不相等的实数根即可.
证明:考察一元二次方程 2x2+3x-7=0.
因为 =32-4×2×(-7) =65>0,
所以方程 2x2+3x-7=0 有两个不相等的实数根.
因此,二次函数 y=2x2+3x-7有两个零点.
例 2
判断二次函数 y=x2-2x-1在区间(2,3)上是否存在零点.
解:根据求根公式可得一元二次方程 x2-2x-1=0 的两个根分别为 x1=1+,x2=1-.
因为 1< <2,
所以 1<1+< 3.
因此,二次函数y=x2-2x-1在区间(2,3)上存在零点.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) a>0时二次函数 y=ax2+bx+c有两个零点.( )
(2) 如果二次函数 y=ax2+bx+c与x轴没有交点,则此二次函数没有零点. ( )
Δ>0时二次函数 y=ax2+bx+c有两个零点.
2. 二次函数 y=ax2+bx+c (a≠0)中若 b2>4ac,则函数
零点的个数为 ( )
A. 0 B. 1 C. 2 D. 不能确定
C
解析:因为b2>4ac,
所以 Δ=b2-4ac>0,
所以 函数有2个零点.
解析
3. 函数 y=(x+2)(x+1) 的零点是_____________.
-2,-1
解析:令(x+2)(x+1)=0,
解得 x=-2或 x=-1,
所以函数的零点是-2, -1.
解析
【跟踪训练】
1. 若 b2-4ac=0,则二次函数 y=ax2+bx+c (a≠0) 零点的个数为 ( )
A. 0个 B.1个 C.2个 D.无法确定
B
解析:因为 b2-4ac=0,
所以一元二次方程 ax2+bx+c=0有两个相等的实数根,
所以二次函数 y=ax2+bx+c 有一个零点.
解析
2. 二次函数 y= (2x+1)(x-5)的零点为 ( )
A. ,-5 B. - ,5
C. 2,- D. -2,
B
解析:因为方程 (2x+1)(x-5)=0 的两个根为x1=-,x2=5,
所以二次函数 y=(2x+1)(x-5) 的零点为- ,5.
解析
3. 二次函数 y=x2-2的零点所在的区间为 ( )
A. (1,0) B. (1,2) C.(2,3) D.(3,4)
B
解析:解方程 x2-2=0得,x=±,
其中1<<2.
解析
4. 已知二次函数的图象如图所示,则此函数的零点为
____________.
-1,1
解析:因为二次函数的图象与x轴交点的横坐标分别为- 1,1,
所以此函数的零点为-1,1.
解析
5. 二次函数 y=x2-ax 的一个零点为2,则a=________.
解析:由题意,x=2是方程x2-ax=0的根,
所以 4-2a=0,解得 a=2.
解析
2
练 习
1. 当 a < 0 时,请填下表:
判别式 =b2-4ac >0 =0 <0
方程 ax2+bx+c=0的根 有两个相异的实数根 x1,2= 有两个相等的实数根 x1=x2=- 没有实数根
判别式 =b2-4ac >0 =0 <0
二次函数 y=ax2+bx+c的图象
判别式 =b2-4ac >0 =0 <0
二次函数 y=ax2+bx+c的零点 有两个零点 x1,2= 有一个零点x=- 无零点
2. 画出二次函数 y=x2-x-2 的图象,并指出该函数
的零点.
解:二次函数 y=x2-x-2 图象如下:
由 x2-x-2=0 得,
x=-1或x=2.
故所求零点为-1,2.
3. 求下列二次函数的零点:
(1) y=(x+1)(x-1);
(2) y=x2-4x;
解:令 y=0,得x1=-l,x2=1,
所以函数的零点为-1和 1.
解:令 y=0,即 x2-4x=0,得x(x-4)=0,
解得x1=0,x2=4,
所以函数的零点为 0 和 4 .
(3) y=-3x2-9;
(4) y=-x2+2x-1.
解:令 y=-3x2-9=0,方程无实数根,
所以函数无零点.
解:令 y=-x2+2x-1=0,即x2-2x+1=0,
得 (x-1)2=0,解得 x=1.
所以函数的零点为1.
3. 3 . 2
从函数观点看一元二次不等式
我们来看下面的问题:
某杂志以每册 2 元的价格发行时,发行量为 10 万册经过调查若单册价格每提高 0.2 元,则发行量就减少 5000 册要使杂志社的销售收入大于 22.4 万元,每册杂志的价格应定在怎样的范围内
设每册杂志价格提高 x 元,则发行量减少
0.5×=
万册,杂志社的销售收人为(2+x)(10-)万元.
根据题意,得 (2+x)(10-) >22.4,
化简,得 5x2-10x+4.8 < 0.
一、一元二次不等式的概念
只含有一个未知数,并且未知数最高次数是 2 的_______________叫作一元二次不等式.
整式不等式
【思考】
不等式 x2+ > 0是一元二次不等式吗
提示:不是,一元二次不等式一定是整式不等式.
我们知道,一元二次方程和相应的二次函数有着密切的联系,一元二次方程的根就是相应二次函数的图象与x轴交点的横坐标.
那么,
● 一元二次不等式和相应的二次函数是否也有内在的联系
二、一元二次不等式和相应的二次函数的对应关系
(1) 关系:(a>0)
判别式 =b2-4ac >0 =0 <0
方程 ax2+bx+c=0的根 有两个相异的实数根 x1,x2 (x1<x2) 有两个相等的实数根 x1=x2=- 没有实数根
判别式 =b2-4ac >0 =0 <0
二次函数 y=ax2+bx+c的图象
判别式 =b2-4ac >0 =0 <0
ax2+bx+c>0的解集 (-∞,x1) ∪ (x2,+∞) (-∞,-) ∪ (-,+∞) R
ax2+bx+c<0的解集 (x1<x2)
【思考】
(1) 有人说:当 Δ>0 时表中的 x1,x2 有三重身份,
你能说出是哪三重身份吗
提示:x1,x2 既是二次函数图象与x轴交点的横坐标 (即二次函数的零点),又是一元二次方程的两个解,还是一元二次不等式解集的区间端点.
(2) 若一元二次不等式 ax2+x-1>0 (a≠0) 的解集为R,
则实数 a 应满足什么条件
提示:结合二次函数图象可知,若一元二次不等式 ax2+x-1>0 (a≠0)的解集为R,
则 解得 a∈ ,
所以不存在a使不等式 ax2+x-1>0 的解集为R.
a>0
1+4a<0
(2) 本质:
方程 ax2+bx+c=0 (a≠0) 和不等式 ax2+bx+c>0
(a>0) 或 ax2+bx+c<0 (a>0) 是函数 y=ax2+bx+c
(a≠0) 的特殊情况,它们之间是一种包含关系,也就是当 y=0 时,函数 y=ax2+bx+c (a≠0) 就转化为方程,当 y>0 或 y<0 时就转化为一元二次不等式.
(3) 应用:
① 解一元二次不等式,
② 已知一元二次不等式的解集求参数,
③ 一元二次不等式的应用问题.
当a<0 时,通过不等式两边同乘以-1,可将问题转化为二次项系数为正的情形,利用表3-3-2解决.
例 1
解下列不等式:
(1) x2-7x+12>0;
(2) -x2-2x+3≥0;
(3) x2-2x+1<0;
(4) x2-2x+2>0.
(1) x2-7x+12>0;
解 方程 x2-7x+12=0 的解为 x1=3,x2=4.
根据 y=x2-7x+12 的图象
可得原不等式的{ x∣x<3 或 x>4}.
(2) -x2-2x+3≥0;
对 于二次项系数为负数的不等式,可以先把二次项系数化成正数,然后再求解.
解 不等式两边同乘以-1,得 x2+2x-3≤0.
方程 x2+2x-3=0 的解为 x1=-3,x2=1.
根据 y = x2+2x-3 的图象,
可得原不等式的解集为 { x∣-3≤x≤1).
(3) x2-2x+1<0;
解 方程 x2-2x+1=0 有两个相同的解x1=x2=1.
根据 y=x2-2x+1的图象,
可得原不等式的解集为 .
(4) x2-2x+2>0.
解 因为 <0,所以方程 x2-2x+2=0 无实数解.
根据 y=x2-2x+2 的图象,
可得原不等式的解集为 R .
练 习
1. (1) 不等式(x-1)(x-3)>0的解集为( )。
A.{ x∣x<1} B.{ x∣x>3}
C.{ x∣x<1 或 x>3} D.{ x∣1<x<3}
(2) 不等式-x2+2x-4>0 的解集为( ).
A. R B.
C. { x∣x>0,x∈R} D.{ x∣x<0,x∈R}.
C
B
2. 解下列不等式:
(1) x2+4x-12>0;
解:该不等式可化为(x+6)(x-2)>0,
解得 x<-6或 x>2,
故原不等式的解集为{ x∣x<-6 或 x>2}.
(2) x2-x+1≤0;
解:该不等式可化为(x-)2+≤0 ,
无解,
故原不等式的解集为 .
(3) 2x2-5x+3<0;
解:该不等式可化为(x-1)(2x-3) <0,
解得 1<x< ,
故原不等式的解集为{ x∣ 1<x< }.
(4) 3x2-x-4>0;
解:该不等式可化为(x+1)(3x-4) >0,
解得 x<-1或 x> ,
故原不等式的解集为{ x∣ x<-1或 x> }.
(5) 2x2+4x+3>0;
解:该不等式可化为2(x+1)2+1>0,
恒成立,
故原不等式的解集为R.
(6) 9x2-6x+1≤0.
解:该不等式可化为(3x-1)2 ≤0,
解得 x=,
故原不等式的解集为{ x∣ x= }.
3. 解下列不等式:
(1) -6x2-x+2<0;
解:不等式可变形为 6x2+x-2>0 ,
对应方程的两根分别为和-,
由 y=6x2+x-2的图象知解集为
{ x∣x <- 或 x> }
(2) 1-4x2≥4x+2;
解:不等式可变形为4x2+4x+1<0,
即(2x+1)2<0,
显然无解,
即解集为 .
(3) 1-3x<x2;
解:不等式可变形为 x2+3x-1>0,
对应方程的两根为 x1,2== ,
由 y=x2+3x-1的图象知解集为
{ x∣x < 或 x > }.
(4) (x-2)(x+2) >1.
解:不等式可变形为 x2-5>0,
对应方程的两根为 x1=-,x2=,
由 y=x2-5 的图象知解集为
{ x∣x<- 或 x> }.
4. 当 x 是什么实数时,函数 y=-x2+5x+14 的值是:
(1) 0
解: -x2+5x+14=0
x2-5x-14=0
(x-7)(x+2) =0
x1=7,x2=-2
(2) 正数
解: -x2+5x+14>0
x2-5x-14<0
(x-7)(x+2) <0
-2<x<7
(3) 负数
解: -x2+5x+14<0
x2-5x-14>0
(x-7)(x+2) >0
x>7 或 x<-2.
5. (1)已知集合 M={x|-4≤x≤7,N={x|x2-x-6>0},
求M∩N;
解:∵集合M = {x∣-4≤x≤7},
N = {x|x2-x-6>0}
= {x∣x<-2或 x>3},
∴ M∩N ={x∣-4≤x<-2 或 3< x≤7};
(2) 已知集合 A={x|x2-4x+3<0},B={x|(x-2)(x-5)
<0},求 A∪B.
解:∵集合A={x|x2-4x+3<0}
={x∣1<x<3},
B={x|(x-2)(x-5)<0}
={x∣2<x<5},
∴ A∪B ={x∣1<x<5}.
例 2
用一根长为 100 m的绳子能围成一个面积大于 600 m的矩形吗 当长、宽分别为多少米时,所围成的矩形的面积最大
解:设矩形一边的长为 x m,则另一边的长为 (50-x) m,其中0<x<50.
由题意,得 x(50-x) >600,
即 x2-50x+600<0,
解得 20<x<30.
所以,当矩形一边的长在 20 m 至 30 m 的范围内取值时,能围成一个面积大于 600 m2 的矩形.
用 S 表示矩形的面积,则
S=x(50-x)
=- (x-25)2+625 (0<x<50).
当x=25 时,S 取得最大值,此时 50-x=25.
答 当矩形的长、宽都为25m时,所围成的矩形的面积最大.
你能用基本不等式来求 x(50-x) 的最大值吗
例 3
某小型服装厂生产一种风衣,日销货量 x 件(x∈N*)与货价 P 元/件之间的关系为 P=160-2x,生产 x 件所需成本为 C=500+30x 元.
问:该厂日产量多大时,日获利不少于1300 元
解 由题意,得 (160-2x)x-(500+30x)>1300,
化简,得 x2-65x+900<0,
解得 20≤x≤45.
答 该厂日产量在20件至45件时,日获利不少于1300元.
例 4
汽车在行驶中,由于惯性的作用,刹车后还要继续向前滑行一段距离才能停住,我们称这段距离为“刹车距离”刹车距离是分析事故产生原因的一个重要因素.
在一个限速为 40 km/h的弯道上,甲乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相碰.
事后现场勘查测得甲车的刹车距离小于 12 m,乙车的刹车距离略超过 10 m. 又知甲两种车型的刹车距离 (单位:m)与车速 x (单位:km/h)之间分别有如下关系:
s甲= 0.1x+ 0.01x, s乙=0.05x+0.005x2.
问:甲、乙两车有无超速现象
一般来说,刹车距离与车速是二次函数关系.
分析 根据汽车的刹车距离可以估计汽车的车速.
解 由题意知,对于甲车,有 0.1x+0.01x2<12,
即 x2+10x-1200<0,
解得 -40<x<30.
这表明甲车的车速低于 30 km/h,未超过规定限速.
对于乙车,有 0.05x+0.005x2>10,
即 x2+10x-2000>0,
解得 x>40 或 x<-50 (不合实际意义,舍去).
这表明乙车的车速超过 40 km/h,超过规定限速.
答 甲车未超过规定限速,乙车超过规定限速.
练 习
1. 如果某厂扩建后计划后年的产量不低于今年的 2倍,
那么明、后两年每年的平均增长率至少是多少
解:设该厂今的产量为a,明、后两年每年的平均增长率至少是x%,则a(1+x%)2≥2a,
解得 x%≥41.4%.
∴ 明、后两年每年的平均增长率至少是41.4%.
2. 销售某种商品,单价为 a 元时,销售量是b. 经市场调
研可以预测,若单价上涨 m%,则销售量将减少.
为了使该商品的销售金额最大,m 应定为多少
解:设原来销售金额为y,
根据题意可知调整后的单价是a·(1+),
售出的数量是 b·(1-),
调整后的销售金额为:
y=a·b·(1+)(1-) =a·b·(1-m2+m)
= - m2 + m +
=[-(m-25)2 +]ab
∵ab均为正,
∴当m=25时,y最大,
故m定为25.
3. 国家为了加强对饮用酒生产的宏观管理,实行征收附
加税政策.已知某种洒每瓶 70 元,不征收附加税时,
每年大约销售 100 万瓶;若政府征收附加税每销售
100 元要征税 R元 (叫作税率 R%),则每年的销售量
将减少 10R 万瓶. 要使每年在此项经营中所收取的附
加税不少于 112 万元,R 应怎样确定
解:设产销量为每年x万瓶,则销售收入为每年70x万元,从中征收的税金为 70x·R%万元,其中 x=100-10R.
由70(100 - 10R)·R%≥112,
即 R2-10R+16 < 0.
解得 2≤R≤8.
故税率定在2% ~ 8%之内,年收附加税额将不低于112万元.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) mx2-5x<0 是一元二次不等式 ( )
(2) 若 a>0,则一元二次不等式 ax2+1>0无解( )
当m=0时是一元一次不等式;
当m≠0时,它是一元二次不等式.
因为a>0,所以不等式ax2+1>0恒成立,即原不等式的解集为R.
(3) 若一元二次方程 ax2+bx+c=0(a≠0) 的两根为x1,x2 (x1<x2),则一元二次不等式 ax2+bx+c<0的解集为{ x∣x1<x<x2 }. ( )
当 a>0时,ax2+bx+c<0的解集为{ x∣x1<x<x2},否则不成立.
2. 不等式 (2x+1)(x-1)>0 的解集是 ( )
A. { x∣-<x<1} B.{ x∣x>1}
C.{ x∣x<1 或 x>2} D. { x∣x<-或 x>1}
D
解析:因为方程 (2x+1)(x-1)=0的解为 x1=-,x2=1,
所以根据函数 y=(2x+1)(x-1)的图象,可得原不等式的解集为{ x∣x<-或 x>1} .
解析
3. 不等式-3x2+5x-4>0 的解集为________.
解析:原不等式变形为 3x2-5x+4<0.
因为Δ= (-5)2-4×3×4=-23<0,
所以由函数 y=3x2-5x+4 的图象可知,
3x2-5x+4<0 的解集为 .
解析
【跟踪训练】
1. 不等式 (-x)(-x)>0 的解集是 ( )
A.{ x∣ <x<}
B. { x∣x> }
C. { x∣x<}
D.{ x∣x<或x> }
D
解析:方程(-x)(-x) =0的两根为 x1=,x2=,所以原不等式的解集为{ x∣x<或x> }.
解析
2.一元二次不等式ax2+bx+2>0(a≠0)的解集是(-, ),
则a+b的值是( )
A.10 B. -10 C.14 D. -14
D
解析:方程ax2+bx+2=0(a≠0)的两个根为-和 ,
-+= - ,-×= ,
所以 a=-12,b=-2,a+b=-14.
解析
3. 某公司每个月的利润 y (单位:万元)关于月份 n 的关
系式为 y=n2-9n+114,则该公司12个月中,利润大
于100万元的月份共有 ( )
A. 4个 B. 5个 C. 6个 D. 7个
C
解析:由题意得 n2-9n+114>100,
解得 n<2或 n>7,
故 n=1,8,9,10,11,12,共6个月.
解析
4. 二次函数 y=x2-4x+3当函数值为负数时 x 的取值范
围是___________.
1<x<3
解析:由于方程 x2-4x+3=0 的两个根为 x1=1,x2=3.
故不等式 x2-4x+3<0 的解集为{ x∣1<x<3}.
解析
5. 不等式-x2+mx+m<0 恒成立的条件是__________.
-4<m<0
解析:-x2+mx+m<0 恒成立,等价于Δ<0,
即 m2+4m<0,
所以-4<m<0.
解析
习题 3.3
感受·理解
1. 证明:函数 y=x2-x+1 没有零点.
解:∵ = b2-4ac
= (-1)2-4×1×1
=1-4 =-3 <0.
∴ 函数 y=x2-x+1没有零点.
2. 设 m 为实数,若函数 y= x2-mx+2 有只有一个零点,
求 m 的值.
解:函数 y=x2-mx2 有且只有一个零点,
一个根,则 =m2-8=0,
所以 m ±2.
3. 设k为实数,若方程 x2-3x+k-3=0 有实数根,求 k
的取值范围.
解:将方程整理得:4x2-12x+k-3=0,有题意知:
=122-4×4×(k-3)<0,
解得:k>12.
∴ k 取值范围是(12,+∞).
故答案为:(12,+∞)
4. 证明:函数 y=5x2-7x-1的一个零点在区间(-1,0)
内,另一个零点在区间(1,2)内.
解:令f(x)=5x2-7x-1,则f(x)在R上是连续函数.
∵ =(-7)2-4×5-(-1) =49+20=69>0,
∴方程 f(x)=0 有两个不等实数根,
即f(x) =5x2-7x-1在R上有两个零点;
又∵f(-1)=5×(-1)2-7×(-1) -1=11>0,
f(0)= -1<0,
∴ 在区间(-1,0)内,函数f(x)=5x2-7x-1存在零点;
又∵ f(1) = 5-7-1=-3<0,
f(2) = 5×22-7×2-1=5>0,
∴在区间(1,2)内,函数f(x)=5x2-7x-1存在零点.
又∵函数f(x)=5x2-7x-1在R上有且仅有两个零点,
∴ 函数f(x)=5x2-7x-1一个零点在区间(-1,0)内,
另一个零点在区间(1,2)内.
5. 解下列不等式:
(1) x(x-1) ≤ 0;
(2) (x+1)(x-5)>0;
解:因为对应方程的两根为0和1,
所以不等式的解集是{x∣0≤x≤1}.
解:因为对应方程的两根为-1和5,
所以不等式的解集是{x∣x<-1或x>5}.
(3) x2-6x+9≤0;
(4) 3x2-7x+2 > 0;
解:因为对应方程为(x-3)2=0,
对应方程的一个根为3,
所以不等式的解集是{x∣x=3}.
解:因为对应方程的两根为2和,
所以不等式的解集为{ x∣x<或x>2}
(5) -2x2-x+6>0;
(6) x2-x+1>0.
解:因为不等式可化为 2x2+x-6≤0,
对应方程的两根为-2和,
所以不等式的解集为{ x∣-2≤ x≤ }.
解:因为对应方程判别式 <0,
所以不等式的解集为R.
6. 解下列不等式:
(1) 2x2-3x>2;
解:∵ 2x2-3x-2>0,
∴ (2x+1)(x-2)>0,
∴x<-或x>2,
∴不等式的解集为{x∣x<-或x>2}.
(2) 3x2-5x+4>0;
解:∵ =25-4×3×4
=-23<0,
∴不等式3x2-5x+4>0的解集为R.
(3) x(x+2) <x(3-x) +1;
解:∵原不等式可化为:2x2-x-1<0,
即(2x-1)(x-1) <0,
∴-<x<1,
∴不等式的解集为{x∣-<x<1}.
(4) (3x-1) (x+1)>4.
解:∵原不等式可化为:3x2+2x-5<0,
即(3x+5)(x-1)>0,
∴ x<- 或 x>1,
∴不等式的解集为:{x∣ x<- 或 x>1}.
7. 当x是什么实数时,函数 y=-x2-8x+20 的值是:
(1) 0
解:-x2-8x+20 =0
x2+8x-20 =0
(x-2)(x+10) =0
x=-10或x=2
(2)正数
解:-x2-8x+20 >0
x2+8x-20 <0
(x-2)(x+10) <0
-10<x<2
(3)负数
解:-x2-8x+20 <0
x2+8x-20 >0
(x-2)(x+10) >0
x<-10 或 x>2
8. 制作一个高为 20 cm 的长方体容器,底面矩形的长比
宽多 10 cm,并且容积不少于 4 000 cm3.
问:底面矩形的宽至少应是多少
解:设底面矩形的宽为 x cm,
由题意可得20x(x+10) ≥ 4000.
即 x2+10x-200≥0,
解得:x≤-20 (舍) 或x≥10.
∴ 底面矩形的宽至少应为10 cm.
9. 已知二次函数y=x2+bx+c的图象与x轴交于A(-1,0),
B(2,0)两点,求关于x的不等式 x2+bx+c>0 的解集.
解:∵ 二次函数 y=x2+bx+c 的图象与x轴交于
A(-1,0),B(2,0) 两点,
∴ -1,2 是关于x的一元二次方程 x2+bx+c=0
的两个实数根,
∴关于x的不等式x2+bx+c>0 的解集为:
{x∣x<-1或x>2}.
思考·运用
10. 设m为实数已知二次函数 y=x2-5x+m 的两个零点都
在区间(0,+∞)内,求 m 的取值范围.
解:二次函数 y=x2-5x+m的图象是一条抛物线,
开口向上,对称轴方程为 x=,
若它的两个零点都在区间(1,+oo)内,
只需满足 =(-5)2-4×1·m>0
f(1)=-4+m>0
解得:4<m<,
∴ m 的取值范围是(4, )
11. (1) k 是什么实数时,方程 x2+2(k-1)x+3k2-11=0
有两个不相等的实数根
解:方程 x2+2(k-1)x+3k2-11=0中,
令 >0,得 4(k-1)2-4(3k2-11)>0,
化简得 k2+k-6<0,
解得 -3<k<2,
所以 k∈(-3,2) 时,方程有两个不相等的实数根;
(2) 已知不等式 x2-2x+k2-1>0 对一切实数 x 恒成立,
求实数k的取值范围.
解:不等式 x2-2x+k2-1>0 对一切实数x恒成立,
∴ <0,即4-4(k2-1) <0,
化简得 k2>2,
解得 k> 或 k<-;
∴实数k的取值范围是(-∞,-)∪(+∞).
12. 已知不等式 ax2+b-1>0的解集是{ x∣3<x<4 },
求实数 a,b 的值.
解:由题意知,a<0,
且 3,4 是方程 ax2+bx-1=0的根.
∴
解得
9a+3b-1=0
16a+4b-1=0
a=-
b=
13. 如图,某房地产开发公司要在矩形地块 ABCD 上规划出一块矩形地块PQCR 建造住宅区为了保护文物,住宅区不能超越文物保护区△AEF的界线EF. 由实地测量知,AB=200 m,AD=160 m,
AE =60 m,AF=40 m.
问:怎样设计矩形住宅区的长和宽,
才能使其面积最大 最大面积是多少
G
解:设PQ交DA于点G,如图所示:
设PQ=x,140≤x≤200,
则GP=200-x,
∵△GPF~△AEF,
∴ FG= (200-x)
∴ PR=DF+FG=120+ (200-x),
∴ SPQCR =x[120+ (200-x)]=-x2+x
=-(x-190)2+,
当x=190 时,即 PR=120+120+(200-190)=时,
SPQCR取得最大值,
故当矩形住宅区的长为190m,宽为m时, SPQCR取得最大值m2.
14. 已知某公司每天生产的某种产品的数量 (单位:百件)
与其成本y (单位:千元)之间的函数解析式可以近似
地用 y=ax2+b+c 表示其中a,b,为常数. 现有实际
统计数据如下表所示:
产品数量x/百件 6 10 20
成本y/千元 104 160 370
产品数量x/百件 6 10 20
成本y/千元 104 160 370
(1) 求a,b,c 的值;
解:将表格中相关数据代入 y=ax2+bx+c.
36a+6b+c=104
得 100a+10b+c=160,
400a+20b+c=370
解得 a=,b=6,c=50.
(2) 若每件产品销售价为 200 元,则该公司每天生产多少
产品时才能盈利 (假设每天生产的产品可以全部售完)
解:由(1)知,y= x2+6x+50(x≥0),
由题意可知 200x×0.1-y>0
即 -x2+14x-50 >0,
解得 4.2< x <23.8
故该公司每天生产产品数量在区间(420,2380)时才能盈利.
探究·拓展
15. (阅读题)重新考察不等式 5x2-10x+4.8<0 这个不等
式的左边可分解因式为(x-1.2)(5x-4). 根据实数乘
法的符号法则,问题可归结为求一元一次不等式组
的两个解集的并集.
x-1.2<0, x-1.2>0.
(1) 和 (2)
5x-4>0 5x-4<0
不等式组(1)的解为 0.8<x<1.2 不等式组(2)无解,从而不等式 5x2-10x+4.8<0 的解集为{ x∣0.8<x<1.2}.
试用上述方法解下面的不等式:
(1) (2x-3)(x+1) >0; (2) (1-x)(2+x)≥0;
(3) <0; (4) ≤0.
(1) (2x-3)(x+1) >0;
解:∵ (2x-3)(x+1)>0,
∴ ,或
解得 x>,或 x<-1,
∴ 原不等式的解集为{x∣ x<-1或x>};
2x-3>0
x+1>0
2x-3<0
x+1<0
(2) (1-x)(2+x)≥0;
解:∵ (1-x)(2+x)≥0,
∴ ,或
解得 -2≤x≤1,或 无解,
∴ 原不等式的解集为{x∣ -2≤x≤1};
1-x≥0
2+x≥0
1-x≤0
2+x≤0
(3) <0;
解:∵ <0 ,
∴ ,或
解得 -3<x<1 ,或无解,
∴ 原不等式的解集为{x∣ -3<x<1 };
x-1<0
x+3>0
x-1 > 0
x+3<0
(4) ≤0.
解:∵ ≤0 ,
∴ ,或
解得 x≥,或 x<-4,
∴ 原不等式的解集为{x∣ x<-4或x≥};
1-2x ≤ 0
x+4>0
1-2x ≥ 0
x+4 < 0
问题与探究
基本不等式的推广
我们已知基本不等式 ≤ (a,b > 0),那么,对于3个正数 a,b,c,是否有
≤
对于4个正数a,b,c,d,是否有
≤
给出一些具体数,借助计算机(器)验证一下,并尝试给出证明. 你还会有什么猜想
阅 读
不等号的演变
在早期,人们使用文字或象征性记号来记述不等关系.例如,荷兰数学家吉拉尔 ( A . Girard,1595—1632) 在他 1629 年所著《代数新发现》一书中,使用下面记号:
A ff B 表示A大于B,B§A 表示B小于A.
1631年,英国数学家奥特雷德 ( W . Oughtred,1574—1660) 在《数学入门》一书中,用符号:
表示大于, 表示小于.
也有传说,用符号:
表示大于, 表示小于.
1634 年,法国数学家厄里岗( P.Herigone ) 在《数学教程》一书中,采用符号:
a3I2b 表示a大于b,b2I3a 表示a小于b.
他的意思是说,因为 3>2,所以 a3>2b ( a,b 为正数),故 a>b,小于号的意思也是这样的.
1631年,英国数学家、望远镜发明者哈里奥特 ( T . Harriot,1560-1621)去世后 10 周年,人们出版了他的遗著《分析术实例》在这本书中,他写道:
大于的记号:a>b表示 a 量大于 b 量,
小于的记号:a<b表示 a 量小于 b 量.
这一简洁优美的记号,不管后人采用怎样的方式去创造不等号最终都无法取代“>”“<”两个记号.“>” “<”直到 18 世纪初才被泛使用.
至于“≠”“≯”“≮”的出现,乃是近代之事. 一般人不使用“≮”“≯”,而使用“≥”“≤”(或“≧”“≦”)两个记号,表示“大于或等于”“小于或等于”.
在数学史上,也有数学家使用“”表示“等于或大于”,“”表示“等于或小于”.
在少数数学著作中,也出现用“∨”表示小于,“∧”表示大于.例如,2∨3表示“2 小于 3”,9∧7表示“9 大于7”,这种写法没有得到广泛传播,更多的数学书只将符号“∨”表示“<”“>”“≤”“≥”中的一种.例如,a∨b表示“a>b”“a<b”“a≥b”“a≤b”中的一种.
高等数学中,还出现“”表示“远小于”,“”表示“远大于”.
在有些计算机语言中,使用“<>”表示“不等于”,“>=”表示“大于或等于”,“<=”表示“小于或等于”.
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
