5.1 函数的概念和图象 课件(共116张PPT)
文档属性
| 名称 | 5.1 函数的概念和图象 课件(共116张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 68.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 21:36:29 | ||
图片预览











文档简介
(共116张PPT)
第5章
函数概念与性质
5 . 1
函数的概念和图象
在现实生活中,我们可能会遇到下列问题:
1. 人口数量变化趋势是我们制定一系列相关政策的依据. 从中国统计年鉴中可以查得我国1979~2014 年人口数据资料(年末)如表5-1-1所示,你能根据该表说出我国人口的变化情况吗
表5-1-1 1979~2014 年我国人口数据表
年份 1979 1984 1989 1994 1999 2004 2009 2014
人口数/百万 975 1044 1127 1199 1258 1300 1335 1368
2. 一物体从静止开始下落,下落的距离 y (单位:m) 与下落时间 x (单位:s) 之间近似地满足关系式 y=4.9x2.
若一物体下落 2s,你能求出它下落的距离吗
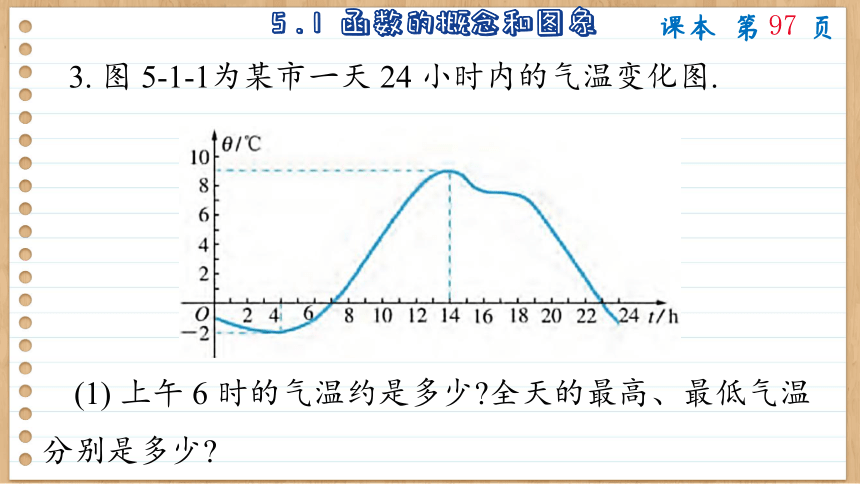
3. 图 5-1-1为某市一天 24 小时内的气温变化图.
(1) 上午 6 时的气温约是多少 全天的最高、最低气温分别是多少
(2) 在什么时刻,气温为 0℃
(3) 在什么时段内,气温在 0℃以上
在上述的每个问题中都含有两个变量,当一个变量的取值确定后,另一个变量的值随之唯一确定.
根据初中学过的知识,每一个问题都涉及一个确定的函数.
这就是它们的共同特点.
● 如何用集合语言来阐述上述 3 个问题的共同特点
第一,每个问题均涉及两个非空数集 A,B.
例如,在第一个问题中,一个集合 A 由年份数组成,即 A={1979,1984,1989,1994,1999,2004,2009,2014};
另一个集合 B由人口数(百万) 组成,即
B={975,1 044,1 127,1 199,1 258,1 300,1 335,1 368}.
第二,每个问题均存在某种对应关系,对于A 中任意元素x ,B 中总有一个元素 y 与之对应.
例如,在第一个问题中,若x (年份)取 1979,则 y (百万) 取 975.
这时,我们说“1979 对应到975”,或者说“输入1979,输出975”,简记为
1979 → 975.
图 5-1-2 所示的“箭头图”可以清楚地表示这种对应关系,这种对应具有“一个输入值对应到唯一的输出值”的特征.
1979
1984
1989
1994
1999
2004
2009
2014
975
1044
1127
1199
1258
1300
1335
1368
一、函数
(1) 概念:
①定义:一般地,给定两个非空实数集合A和B,如果按照某种对应关系f,对于集合A中的每一个实数x,在集合B中都有______的实数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数.
唯一
② 记法:y=f(x),x∈A.
③定义域:x叫作自变量,集合A叫作函数的定义域;
值域:所有输出值y组成的集合{y∣y=f(x),x∈A}
称为函数的值域.
(2)本质:函数的集合定义.
【思考】
1. 对于函数 f:A→B,值域一定是集合B吗 为什么
提示:不一定.值域是集合B的子集.
2. 对应关系f必须是一个解析式的形式吗 为什么
3. f(x)的含义是什么
提示:不一定.可以是数表,也可以是图象.
提示:集合A中的数x在对应关系f的作用下对应的数.
考察本章引言中的问题(1),对于每一个 x (x∈(0,+∞)),都有唯一的实数 y=π 与 x 对应. 因此,y=π (x∈(0,+∞)) 是x的函数.
由函数定义还可知,虽然两个函数的表达形式不同,但如果其对应关系相同,定义域相同,那么这两个函数就是同一个函数.
例如函数 y=x2 (x∈(0,+∞))与函数 s=t2(t∈(0,+∞)) 是同一个函数.
如果两个函数的表达式相同,即其对应关系相同,但定义域不同,那么这两个函数就是不同的函数.
例如本章引言问题(2)中函数y=x2(x∈R)的定义域是R,函数 y=x2( x∈(0,+∞)) 的定义城是(0,+∞),它们是两个不同的函数.
给定函数时要指明函数的定义域.
对于用表达式表示的函数,如果没有指明定义域,那么,就认为函数的定义域是指使函数表达式有意义的输入值的集合.
二、同一个函数
前提条件 _______相同
_________相同
结论 这两个函数是同一个函数
定义域
对应关系
【思考】
函数有定义域、对应关系和值域三要素,为什么判断两个函数是否是同一个函数,只看定义域和对应关系
提示:由函数的定义域和对应关系可以求出函数的值域,所以判断两个函数是否是同一个函数,只看定义域和对应关系即可.
三、常见的函数的定义域和值域
函数 一次函数 反比例函数
对应关系 y=ax+b (a≠0) y= (k≠0)
定义域 R {x∣x≠0}
值域 R {y∣y≠0}
函数 二次函数
____ ____
对应关系 y=ax2+bx+c (a≠0) y=ax2+bx+c (a≠0)
定义域 R R
值域
a>0
a<0
例 1
判断下列对应是否为函数:
解:对于任意一个非零实数x , 由x唯一确定,所以当 x≠0 时 x→ 是函数,这个函数也可以表示为 f(x)= (x≠0).
(1) x→,x≠0,x∈R;
(2) x → y,这里 y2=x,x∈N,y∈R;
解 考虑输入值为4,即当 x=4 时输出值y由 y2=4 给出,得 y=2 和 y=-2.
这里一个输入值与两个输出值对应,所以,x → y (y2=x,x∈N,y∈R) 不是函数.
(3) 当x为有理数时,x → 1;当x为无理数时,x → 0 .
解 由题意知,对于任意的有理数 x,总有唯一的元素 1与之对应;对于任意的无理数 x,总有唯一的元素 0 与之对应.因此,根据函数的定义,可知这个对应是函数,可以表示为
1, x 为有理数
y =
0, x为无理数
例 2
求下列函数的定义域:
(1) f(x) =;
解 当 x-1≥0,即 x≥1 时, 在实数范围内有意义;当 x-1<0,即 x<1时, 在实数范围内没有意义.
因此,这个函数的定义域是{x∣x≥1}.
(2) g(x) =.
解:当 x+1≠0,即 x≠ -1时,有意义;
当 x+1=0时,即 x=-1时, 没有意义.
因此,这个函数的定义域是{x∣x≠-1 ,且x∈R}.
例 3
求下列函数的值域:
(1) f(x) =(x-1)2-1,x∈{-1,0,1,2,3};
解 函数的定义域为{-1,0,1,2,3}.
因为 f(-1) =[(-1) -1]2+1=5,
f(0)=2,f(1)=1,f(2)=2,f(3)=5,
所以这个函数的值域为{1,2,5}.
(2) f(x) =(x-1)2+1.
解 函数的定义域为 R .
因为(x-1)2+1≥1,
所以这个函数的值域为{y∣y≥1}.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1)“y=f(x)”表示的是“y等于f与x的乘积”. ( )
(2) 根据函数的定义,定义域中的任何一个x可以对应着值域中不同的y.( )
(3) 在研究函数时,除用符号f(x)外,还可用g(x),F(x),G(x)等来表示函数. ( )
2.下列两个变量之间的关系不是函数关系的是 ( )
A.出租车车费与出租车行驶的里程
B.商品房销售总价与商品房建筑面积
C.铁块的体积与铁块的质量
D.人的身高与体重
D
解析:A.出租车车费与行程是函数关系;B.商品房销售总价与建筑面积是函数关系;C.铁块的体积与质量是函数关系;D.人的身高与体重不是函数关系.
解析
3. 如图能表示函数关系的是____________.
①②④
解析:由于③中的2与1和3同时对应,故③不是函数关系.
解析
【课堂检测·素养达标】
1.对于函数f:A→B,若 a∈A,b∈A,则下列说法错误的是 ( )
A. f(a)∈B
B. f(a)有且只有一个
C.若 f(a)=f(b),则a=b
D.若 a=b,则f(a)=f(b)
C
解析:对于函数f:A→B,a∈A,b∈A,则根据函数的定义,f(a)∈B,且 f(a)唯一,故若 a=b,则 a,b 代表集合A中同一个元素,这时,有 f(a)=f(b),故 A,B,D 都对.但若f(a)=f(b),则不一定有a=b,如f(x)=x2,显然f(-1)=f(1) =1,但-1≠1,故C错误.
解析
2.如表表示y是x的函数,则该函数的定义域是________,
值域是_______________.
x 0<x<1 1≤x<2 2≤x<3 3≤x≤4
y 1 2 3 4
(0,4]
{1,2,3,4}
解析:由题表可知,函数的自变量x从0开始至4,每个数都有意义,所以定义域为(0,4];该函数是一个分段函数,从表中的数据可知,y只能取到1,2,3,4 这四个数,所以值域为{1,2,3,4}.
解析
3. 若函数 y=x2-3x 的定义域为{-1,0,2,3},则其
值域为_______________.
{-2,0,4}
解析:依题意,当x=-1时,y=4;当x=0时,y=0;
当x=2时,y=-2;当x=3时,y=0,
所以函数 y=x2-3x 的值域为{-2,0,4}.
解析
4.下列对应关系是集合P上的函数的是______.(填序号)
①P=Z,Q=N*,对应关系f:对集合P中的元素取绝对值与集合Q中的元素相对应;
②P={-1,1,-2,2},Q={1,4},对应关系f:x→y=x2,x∈P,y∈Q;
③P={三角形},Q={x∣x>0},对应关系f:对P中的三角形求面积与集合Q中的元素对应.
②
练 习
1. 某班级学号为 1~6 的学生参加数学测试的成绩如下表
所示,试将学号与成绩的对应关系用“箭头图”表示
在下图中.
学 号 1 2 3 4 5 6
成 绩 80 75 79 80 98 80
学 号 1 2 3 4 5 6
成 绩 80 75 79 80 98 80
1
2
3
4
5
6
75
79
80
98
2. 从甲地到乙地的火车票价为 80 元,儿童乘火车时,按
照身高选择免票、半票或全票. 选购票种的规则如下表
所示:
身高 h/m 购票款数/元
h≤1.2 0
1.2<h≤1.5 40
h>1.5 80
身高 h/m 购票款数/元
h≤1.2 0
1.2<h≤1.5 40
h>1.5 80
(1) 若儿童身高h为输入值,相应的购票钱款为输出值,
则 1.0→________,1.3→_______,1.6→________;
(2) 若购票钱款为输入值,儿童身高 h 为输出值,则
0→__________,40→______________.
0
40
80
h≤1.2
1.2<h≤1.5
3. 判断下列对应是否为从 A 到 B 的函数:
(1) A={1,2,3,4,5},B={0,2,4,6,8},
对任意的 x∈A,x→2x;
解 x=5∈A,2x=10 B,故不是函数.
综上所述,结论是:
对应 x→2x 不是从A到B的函数.
(2) A= {1,2,3,4,5},B={x∣x<10,x∈N,对任
意的 x∈A,x→2x+1;
解:x=1∈A → 2x+1=3∈B;
x=2∈A → 2x+1=5∈B;
x=3∈A → 2x+1=7∈B;
x=4∈A → 2x+1=9∈B;满足函数的定义.
综上所述,结论是:对应 x→ 2x+1是从A到B的函数.
(3) A=B=N*,对任意的 x∈A,x→x-1;
解 x=1∈A,x-1=0 B,故不是函数.
综上所述,结论是:
对应x→x-1不是从A到B的函数.
(4) A为正实数集,B=R,对任意的 x∈A,x→x 的算
术平方根.
解 任一个正实数均对应唯一的算术平方根,且算术平方根在实数范围内,
即 >0,x∈A,则存在唯一实数∈R与之对应,满足函数的定义.
综上所述,结论是:对应 x → 是从A到B的函数.
4. 判断下列对应是否为函数:
(1) x→-x,x∈R;
(2) x→1,x∈R;
(3) x→y,其中 y=∣x∣,x∈R,y∈R;
(4) t→s,其中s=t,t∈R,s∈R;
(5) x→y,其中y=x,x∈ [0,+∞),y∈R;
(6) x→y,其中y为不大于的最大整数,x∈R,y∈Z.
是
是
是
是
不是
是
5. 已知函数f(x)=x-x2,求f(0),f(1),f(),f(n+1)-f(n).
解 ∵f(x) = x-x2;
∴f(0) = 0-02 = 0;
f(1) = 1-12 = 0;
f() = -()2 = - = ;
f(n+1) -f(n) =(n+1)-(n+1)2-(n-n2)
=n+1-n2-2n-1-n+n2
=-2n
6. 求下列函数的定义域:
(1) f(x)= 1-3x;
(2) f(x)= ;
解:R.
解 由 x2-1≠0,得 x≠±1,
∴函数f(x)的定义域为{x∣x≠±1 }.
(3) f(x) = + ;
2+x>0
解 由 得-2≤x≤1,
1-x≥0
∴函数f(x)的定义域为[-2,1].
(4) f(x) = +.
x+1≥0
解 由 得 x≥-1且 x≠0,
x≠0
∴函数f(x)的定义域为[-1,0) ∪(0,+∞).
7. 求下列函数的值域:
(1) f(x)=x2+x,x∈{l,2,3};
解 函数的定义域为{1,2,3},
∵ f(1)=12+1=2,f(2)=6,f(3)=12.
∴ 函数f(x)的值域为{2,6,12}.
(2) f(x)=(x-1)2-1;
解 函数的定义域为R,
∵ (x-1)2-1>-1,
∴函数f(x)的值域为[-1,+∞).
(3) f(x)=x+1,x∈(1,2].
解 ∵ x∈(1,2],
∴ x+l∈(2,3],
∴函数f(x)的值域为(2,3].
在初中,我们已学过函数的图象,并能作出函数 y=2x-1,y= (x≠0)以及 y=x2 的图象社会生活中还有许多函数图象的例子,如图所示的心电图、示波图等.
四、函数的图象
(1) 定义
将自变量的一个值x0作为_______,相应的___________作为纵坐标,就得到坐标平面上的一个点(x0,f(x0)).
当自变量取遍函数定义域A中的每一个值时,就得到一系列这样的点.所有这些点组成的图形就是函数 y=f(x)的图象.
横坐标
函数值f(x0)
(2) 集合表示:
所有这些点组成的集合(点集)为________________,
即_________________________.
(3)本质:函数对应的图形,即几何意义.
{(x,f(x)) ∣x∈A}
{(x,y) ∣y=f(x),x∈A}
所有这些点组成的图形就是函数 y=f(x) 的图象.
例如,初中学习过的 y= 的图象就是由点集 {(x,y) ∣y=,x≠0,x∈R}中元素(点) 组成的图形.
【思考】
集合{x∣y=f(x),x∈A}、{y∣y=f(x),x∈A} 能表示函数的图象吗 为什么
提示:不能. 上述两个集合都是数集,不是点集. 因此不能表示函数的图象.第一个集合表示函数的定义域,第二个集合表示函数的值域.
例 4
试画出下列函数的图象:
(1) f(x) = x+1;
(2) f(x) = (x-1)2+1,x∈[1,3).
解:描点作出图象,函数图象分别如图 5-1-4 和 5-1-5 所示.
函数 f(x)=(x-1)2+1, x∈[1,3) 的图象为函数g(x)=(x -1)2+1,x∈R 的图象上 x∈[1,3) 的一段. 其中,点(1,1) 在图象上,用实心点表示;而点(3,5)不在图象上,用空心点表示.
例 5
在 5.1节开头的第一个问题中,如果把人口数 y (百万)看作年份 x 的函数,试根据表 5-1-1,画出这个函数的图象.
解 由表5-1-1的数据,西出的函数图象是8个点,如图 5-1-6所示.
思 考
设函数 y=f(x) 的定义域为 A,集合 P= {(x,y)∣y= f(x). x∈A}与Q={y∣y=f(x), x∈A }相等吗 请说明理由.
例 6
试画出二次函数 f(x)=x2+1的图象,并根据图象回答下列问题:
(1) 比较 f(-2),f(1),f(3) 的大小;
(2)若0<x1<x2,试比较 f(x1)与f(x2)的大小.
解 函数图象如图 5-1-7.
(1) 比较 f(-2),f(1),f(3) 的大小;
解 根据图 5-1-7(1),容易发现
f(-2) =f(2),
f(1)<f(2)<f(3).
所以 f(1)<f(-2)<f(3).
(2) 若0<x1<x2,试比较 f(x1)与f(x2)的大小.
解 根据图 5-1-7(2),容易发现
当0<x1<x2 时,
f(x1) <f(x2).
思 考
在例 6(2)中,
(1) 如果把“0<x1<x2”改为“x1<x2<0”,那么 f(x1)与f(x2)哪个大
(2) 如果把“0<x1<x2”改为“∣x1∣<∣x2∣”,那么 f(x1) 与 f(x2) 哪个大
请结合图象回答上述两个问题,并用不等式的基本知识来解决例 6及上述思考中的问题.
信息技术
下面我们介绍在 Excel 工作表中用“描点连线”的方法绘制函数 f(x)=(x-1)2+1的图象,不妨作 x∈[-2,2]上的图象.
(1)第一列产生自变量的值:在单元格 A1,A2 内分别输入-2,-1.9,选中这两个单元格后,按住鼠标左键并向下方拖曳“填充柄”,如图 5-1-8,直到单元格内出现填充值 2 时为止.
(2) 第二列产生对应的函数值: 如图 5-1-9,在 B1 内输入“=(A1-1)^2+1”,敲回车键或在编辑栏内选中“√”,拖曳 B1 的填充柄至所需的单元格(或双击 B1 的填充柄),得到与第一列相对应的函数值.
(3) 成图:光标置于数据区的任一位置,插入“图表”,选择“XY散点图/无数据点平滑线散点图”,点击“完成”,便得函数 f(x) =(x-1)2+1在区间[-2,2 ]上的图象,如图 5-1-10.
你能用上面的方法绘制函数 f(x)=x3的图象吗
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 已知函数 y=f(x),x∈A,若x0 A,则点(x0,f(x0))一定不在函数的图象上. ( )
(2)直线 x=a 和函数 y=f(x),x∈[m,n]的图象有1个交点. ( )
(3) 函数的图象一定是连续的. ( )
2. (多选题)下列坐标系中的曲线或直线,能作为函数
y=f(x)的图象的有 ( )
BD
解析:能作为函数的图象,必须符合函数的定义,即定义域内的每一个x只能有唯一的y与x对应,故BD可以,AC不可以.
解析
3. 函数 y=x+1,x∈Z,且∣x∣<2的图象是________.
(填序号)
③
解析:由题意知,函数的定义域是{-1,0,1},值域是{0,1,2},函数的图象是三个点,故③正确.
解析
【课堂检测·素养达标】
1. 函数 y=x0 的图象是 ( )
B
解析
解析:因为函数 y=x0的定义域为{x|x≠0},所以排除A,C. 又 y=x0=1,所以排除D.
2. 函数 y= 的大致图象只能是 ( )
B
解析
解析:函数 y= 的大致图象由 y= 的图象向左平移2个单位得到.
解析:因为二次函数的图象过(4,0),
所以16a+4b+c=0.①又过点(0,2),所以c = 2.②
由顶点坐标为(4,0)可知 x=-=4.③
由①②③可解得 a=,b=-1,c=2,所以 abc=-.
3. 二次函数f(x) =ax2+bx+c的图象的顶点为(4,0),且过点(0,2),则abc等于 ( )
A. -6 B.11 C. - D.
C
解析
4. 若函数y=f(x)的图象经过点(0,1),那么函数y=f(x+4)
的图象经过点___________.
(-4,1)
解析
解析:y=f(x+4) 可以认为把 y=f(x) 向左移了4个单位,由 y=f(x) 经过点(0,1),易知 f(x+4) 经过点(-4,1).
练 习
1. 画出下列函数的图象:
(1) f(x)=2x-1;
(2) f(x)=2x-1,x∈ [-1,2);
(3) f(x)=,x∈(0,+∞);
(4) f(x) = +1,x∈(0, +∞);
(5) f(x) = x2,x∈[-1,2];
(6) f(x)=(x-1)2,x∈[0,3].
2. 先画出下列函数的图象,再求出每个函数的值域:
(1) f(x)=(x-1)2,x∈{- 1,0,1,2};
解 由定义域为{- 1,0,1,2}知,
其函数图象就是四个点:
A(-1,4),B(0,1),C(1,0),D(2,1),图象如图所示.
其值域为{4,1,0}.
(2) f(x)=x2,x∈[1,2);
解 函数 f(x)=x2,x∈[1,2) 的图象是抛物线 x2=y落在第一象限内的一部分,其图象如图所示.
函数 f(x)=x2,x∈[1,2)为增函数,
故值域为[f(1),f(2))=[1,4)
(3) f(x)=,x∈[1, 3);
解 ∵x∈[1,3),f(x)=,
∴ 其图象落在第一象限,且是反比例函数 f(x)=图象的一部分.
图象如图所示.
函数 f(x)=,x∈[1,3) 为减函数,
故其值域为(f(3),f(1)] = (,1]
(4) f(x)= ,x为正实数.
解 ∵x>0,故f(x)=>0,其图象在第一象限内,
它是抛物线 y2=x (x>0,y>0) 在第一象限内的部分.
其图象如图所示.
函数f(x)=,x>0 为增函数,
故值域为(f(0),+∞)=(0,+∞ )
3. 根据如图所示的函数 y=f(x) 的图象填空:
(1) f(0)=_______,f(1)= _______,
f(2) =_______.
(2) 若-1<x1<x2<1,则f(x1)与 f(x2)
的大小关系是___________.
2
3
0
f(x1)< f(x2)
习题 5.1
感受·理解
1. 已知函数 y=5x-2.
(1) 当x=0,1,5时,分别求出y的值;
解 ∵函数 y=5x-2,
∴当x=0时,y=5×0-2=-2;
当x=1时,y=5×1-2=3;
当x=5时,y=5×5-2=23;
(2) 当y=0,1,5时,分别求出x的值.
解 令5x-2=0,解得 x=,∴当y=0时,x=;
令5x-2=1,解得 x=,∴当y=1时, x=;
令5x-2=5,解得 x=,∴当y=5时, x=.
2. 判断下列对应 f 是否为从集合 A 到集合 B 的函数:
(1) A={,1,};B ={-6,-3,1},f()=-6,
f(1)= -3,f()=1;
满足函数的定义,则f为从集合A到集合B的函数.
(2) A={1,2,3},B={7,8,9},f(1)=f(2)=7,
f(3)=8;
满足函数的定义,f是从集合A到集合B的函数.
(3) A=B={1,2,3},f(x) = 2x-1;
∵f(2)=5,不满足条件.
故f不是从集合A到集合B的函数;
(4) A=B={ x∣x ≥ -1},f(x)=2x+1;
满足函数的定义,则f是从集合A到集合B的函数;
(5) A=Z,B={-1,1},n为奇数时,f(n)=-1;
n为偶数时,f(n) = 1.
满足函数的定义,则f是从集合A到集合B的函数.
3. 求下列函数的定义域、值域,并画出图象:
(1) f(x)=3x;
解 函数 f(x)=3x 定义域为R,值域为R,图象如下:
(2) f(x)=-3x+1;
解 函数 f(x)=-3x+1定义域为R,值域为R,图象如下:
(3) f(x)= -;
解 定义域为(-∞,0)∪(0,+∞),
值域为 (-∞,0)∪(0,+∞),
图象如下:
(4) f(x)= -+1;
解 定义域为(-∞,0)∪(0,+∞),
值域为 (-∞,1)∪(1,+∞),
图象如下:
(5) f(x)=1-x2;
解 定义域为R,
值域为 (-∞,1],
图象如下:
(6) f(x) =x2+2x.
解 定义域为R,
值域为[-1,+∞),
图象如下:
4. 判断下列各组函数是否是同一个函数,并说明理由:
(1) y=x,y=;
解 不是.
∵y=x 的定义域为R,
而y=的定义域为{x∣x≠0},
∴这两个函数的定义域不同.
(2) y=x2,y=x2,x∈[0,+∞);
解 不是.
因为两个函数的定义域不同
(3) y=x,s=t;
解 是.
虽然两个函数的变量不同,
但定义域都是 R,对应关系也相同.
(4) f(x)=1,g(x)=1.
解 是.
因为两个函数的定义域相同,
对应关系也相同.
思考·运用
5. 已知函数 f(x) = ax+b,且 f(3) = 7,f(5) =-1,
求 f(0),f(1) 的值.
解 ∵ f(x)=ax+b,且 f(3)=7,f(5)=-1,
3a+6=7
∴ ,解得a=-4,b=19.
5a+b=-1
则 f(x) =-4x+19,则 f(0) =19,
f(1) = - 4+19=15.
6. 直线x=a和函数y=x2+1的图象的公共点可能有几个
解 由函数的定义知
直线 x=a和函数 y=a+1的图象有且仅有一个公共点.
7. 已知f(t)=,g(t)=,求证:f(t)-g(t)=-2g(t2).
证明:∵ f(t)= ,g(t)=,
∴ f(t)-g(t)= -
=
= = -2g(t2).
8. 如果函数 f(x)与 g(x)分别由下表给出,那么
f(f(1))=__________,f(g(2))=__________,
g(f(3))=__________,g(g(4))=__________.
x 1 2 3 4
f(x) 2 3 4 1
x 1 2 3 4
g(x) 2 1 4 3
3
2
3
4
9. 设函数 f(x)=2x+3,函数 g(x)=3x-5,
求 f(g(x)),g(f(x)).
解 ∵f(x)=2x+3,g(x)=3x-5,
∴f(g(x))=2g(x)+3=2(3x-5)+3=6x-7,
g(f(x))=3f(x)-5=3(2x+3)-5=6x+4.
探究·拓展
10. 已知集合 A=R,B={-1,1},对应关系 f 如下:
当x为有理数时,f(x)=-l;
当x为无理数时,f(x)=1.
该对应是从集合 A 到集合 B 的函数吗
解 ∵A=R,B={-1,1}都是非空数集,
且对于集合A中的任意一个数x,在对应关系f的作用下,
在集合B中都有唯一的一个确定的数f(x)与之对应,
故该对应是从集合A到集合B的一个函数.
11. (操作题)将一枚子投掷 10 次,并将每次子向上的点数
记录在下表中规定对应关系f:对每一投掷序号 n(n=
1,2,···,10) 对应到这次子的向上点数. 试判断对
应 f 是否为函数. 若是,这个函数值域一定是集合{1,
2,3,4,5,6}吗
投掷序号 1 2 3 4 5 6 7 8 9 10
向上点数 3 2 3 6 4 5 3 2 4 5
∵对于任意一个序号n都有唯一的数与之对应,
∴对应f是函数因为在函数值中,集合{1,2,3,4,5,6}中的数并不一定每个都出现,
由上表可以看出,此函数的值域为{2,3,4,5,6},
∴ 这个函数的值域不一定是{1,2,3,4,5,6}.
本课结束
This lesson is over
THANKS!
第5章
函数概念与性质
5 . 1
函数的概念和图象
在现实生活中,我们可能会遇到下列问题:
1. 人口数量变化趋势是我们制定一系列相关政策的依据. 从中国统计年鉴中可以查得我国1979~2014 年人口数据资料(年末)如表5-1-1所示,你能根据该表说出我国人口的变化情况吗
表5-1-1 1979~2014 年我国人口数据表
年份 1979 1984 1989 1994 1999 2004 2009 2014
人口数/百万 975 1044 1127 1199 1258 1300 1335 1368
2. 一物体从静止开始下落,下落的距离 y (单位:m) 与下落时间 x (单位:s) 之间近似地满足关系式 y=4.9x2.
若一物体下落 2s,你能求出它下落的距离吗
3. 图 5-1-1为某市一天 24 小时内的气温变化图.
(1) 上午 6 时的气温约是多少 全天的最高、最低气温分别是多少
(2) 在什么时刻,气温为 0℃
(3) 在什么时段内,气温在 0℃以上
在上述的每个问题中都含有两个变量,当一个变量的取值确定后,另一个变量的值随之唯一确定.
根据初中学过的知识,每一个问题都涉及一个确定的函数.
这就是它们的共同特点.
● 如何用集合语言来阐述上述 3 个问题的共同特点
第一,每个问题均涉及两个非空数集 A,B.
例如,在第一个问题中,一个集合 A 由年份数组成,即 A={1979,1984,1989,1994,1999,2004,2009,2014};
另一个集合 B由人口数(百万) 组成,即
B={975,1 044,1 127,1 199,1 258,1 300,1 335,1 368}.
第二,每个问题均存在某种对应关系,对于A 中任意元素x ,B 中总有一个元素 y 与之对应.
例如,在第一个问题中,若x (年份)取 1979,则 y (百万) 取 975.
这时,我们说“1979 对应到975”,或者说“输入1979,输出975”,简记为
1979 → 975.
图 5-1-2 所示的“箭头图”可以清楚地表示这种对应关系,这种对应具有“一个输入值对应到唯一的输出值”的特征.
1979
1984
1989
1994
1999
2004
2009
2014
975
1044
1127
1199
1258
1300
1335
1368
一、函数
(1) 概念:
①定义:一般地,给定两个非空实数集合A和B,如果按照某种对应关系f,对于集合A中的每一个实数x,在集合B中都有______的实数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数.
唯一
② 记法:y=f(x),x∈A.
③定义域:x叫作自变量,集合A叫作函数的定义域;
值域:所有输出值y组成的集合{y∣y=f(x),x∈A}
称为函数的值域.
(2)本质:函数的集合定义.
【思考】
1. 对于函数 f:A→B,值域一定是集合B吗 为什么
提示:不一定.值域是集合B的子集.
2. 对应关系f必须是一个解析式的形式吗 为什么
3. f(x)的含义是什么
提示:不一定.可以是数表,也可以是图象.
提示:集合A中的数x在对应关系f的作用下对应的数.
考察本章引言中的问题(1),对于每一个 x (x∈(0,+∞)),都有唯一的实数 y=π 与 x 对应. 因此,y=π (x∈(0,+∞)) 是x的函数.
由函数定义还可知,虽然两个函数的表达形式不同,但如果其对应关系相同,定义域相同,那么这两个函数就是同一个函数.
例如函数 y=x2 (x∈(0,+∞))与函数 s=t2(t∈(0,+∞)) 是同一个函数.
如果两个函数的表达式相同,即其对应关系相同,但定义域不同,那么这两个函数就是不同的函数.
例如本章引言问题(2)中函数y=x2(x∈R)的定义域是R,函数 y=x2( x∈(0,+∞)) 的定义城是(0,+∞),它们是两个不同的函数.
给定函数时要指明函数的定义域.
对于用表达式表示的函数,如果没有指明定义域,那么,就认为函数的定义域是指使函数表达式有意义的输入值的集合.
二、同一个函数
前提条件 _______相同
_________相同
结论 这两个函数是同一个函数
定义域
对应关系
【思考】
函数有定义域、对应关系和值域三要素,为什么判断两个函数是否是同一个函数,只看定义域和对应关系
提示:由函数的定义域和对应关系可以求出函数的值域,所以判断两个函数是否是同一个函数,只看定义域和对应关系即可.
三、常见的函数的定义域和值域
函数 一次函数 反比例函数
对应关系 y=ax+b (a≠0) y= (k≠0)
定义域 R {x∣x≠0}
值域 R {y∣y≠0}
函数 二次函数
____ ____
对应关系 y=ax2+bx+c (a≠0) y=ax2+bx+c (a≠0)
定义域 R R
值域
a>0
a<0
例 1
判断下列对应是否为函数:
解:对于任意一个非零实数x , 由x唯一确定,所以当 x≠0 时 x→ 是函数,这个函数也可以表示为 f(x)= (x≠0).
(1) x→,x≠0,x∈R;
(2) x → y,这里 y2=x,x∈N,y∈R;
解 考虑输入值为4,即当 x=4 时输出值y由 y2=4 给出,得 y=2 和 y=-2.
这里一个输入值与两个输出值对应,所以,x → y (y2=x,x∈N,y∈R) 不是函数.
(3) 当x为有理数时,x → 1;当x为无理数时,x → 0 .
解 由题意知,对于任意的有理数 x,总有唯一的元素 1与之对应;对于任意的无理数 x,总有唯一的元素 0 与之对应.因此,根据函数的定义,可知这个对应是函数,可以表示为
1, x 为有理数
y =
0, x为无理数
例 2
求下列函数的定义域:
(1) f(x) =;
解 当 x-1≥0,即 x≥1 时, 在实数范围内有意义;当 x-1<0,即 x<1时, 在实数范围内没有意义.
因此,这个函数的定义域是{x∣x≥1}.
(2) g(x) =.
解:当 x+1≠0,即 x≠ -1时,有意义;
当 x+1=0时,即 x=-1时, 没有意义.
因此,这个函数的定义域是{x∣x≠-1 ,且x∈R}.
例 3
求下列函数的值域:
(1) f(x) =(x-1)2-1,x∈{-1,0,1,2,3};
解 函数的定义域为{-1,0,1,2,3}.
因为 f(-1) =[(-1) -1]2+1=5,
f(0)=2,f(1)=1,f(2)=2,f(3)=5,
所以这个函数的值域为{1,2,5}.
(2) f(x) =(x-1)2+1.
解 函数的定义域为 R .
因为(x-1)2+1≥1,
所以这个函数的值域为{y∣y≥1}.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1)“y=f(x)”表示的是“y等于f与x的乘积”. ( )
(2) 根据函数的定义,定义域中的任何一个x可以对应着值域中不同的y.( )
(3) 在研究函数时,除用符号f(x)外,还可用g(x),F(x),G(x)等来表示函数. ( )
2.下列两个变量之间的关系不是函数关系的是 ( )
A.出租车车费与出租车行驶的里程
B.商品房销售总价与商品房建筑面积
C.铁块的体积与铁块的质量
D.人的身高与体重
D
解析:A.出租车车费与行程是函数关系;B.商品房销售总价与建筑面积是函数关系;C.铁块的体积与质量是函数关系;D.人的身高与体重不是函数关系.
解析
3. 如图能表示函数关系的是____________.
①②④
解析:由于③中的2与1和3同时对应,故③不是函数关系.
解析
【课堂检测·素养达标】
1.对于函数f:A→B,若 a∈A,b∈A,则下列说法错误的是 ( )
A. f(a)∈B
B. f(a)有且只有一个
C.若 f(a)=f(b),则a=b
D.若 a=b,则f(a)=f(b)
C
解析:对于函数f:A→B,a∈A,b∈A,则根据函数的定义,f(a)∈B,且 f(a)唯一,故若 a=b,则 a,b 代表集合A中同一个元素,这时,有 f(a)=f(b),故 A,B,D 都对.但若f(a)=f(b),则不一定有a=b,如f(x)=x2,显然f(-1)=f(1) =1,但-1≠1,故C错误.
解析
2.如表表示y是x的函数,则该函数的定义域是________,
值域是_______________.
x 0<x<1 1≤x<2 2≤x<3 3≤x≤4
y 1 2 3 4
(0,4]
{1,2,3,4}
解析:由题表可知,函数的自变量x从0开始至4,每个数都有意义,所以定义域为(0,4];该函数是一个分段函数,从表中的数据可知,y只能取到1,2,3,4 这四个数,所以值域为{1,2,3,4}.
解析
3. 若函数 y=x2-3x 的定义域为{-1,0,2,3},则其
值域为_______________.
{-2,0,4}
解析:依题意,当x=-1时,y=4;当x=0时,y=0;
当x=2时,y=-2;当x=3时,y=0,
所以函数 y=x2-3x 的值域为{-2,0,4}.
解析
4.下列对应关系是集合P上的函数的是______.(填序号)
①P=Z,Q=N*,对应关系f:对集合P中的元素取绝对值与集合Q中的元素相对应;
②P={-1,1,-2,2},Q={1,4},对应关系f:x→y=x2,x∈P,y∈Q;
③P={三角形},Q={x∣x>0},对应关系f:对P中的三角形求面积与集合Q中的元素对应.
②
练 习
1. 某班级学号为 1~6 的学生参加数学测试的成绩如下表
所示,试将学号与成绩的对应关系用“箭头图”表示
在下图中.
学 号 1 2 3 4 5 6
成 绩 80 75 79 80 98 80
学 号 1 2 3 4 5 6
成 绩 80 75 79 80 98 80
1
2
3
4
5
6
75
79
80
98
2. 从甲地到乙地的火车票价为 80 元,儿童乘火车时,按
照身高选择免票、半票或全票. 选购票种的规则如下表
所示:
身高 h/m 购票款数/元
h≤1.2 0
1.2<h≤1.5 40
h>1.5 80
身高 h/m 购票款数/元
h≤1.2 0
1.2<h≤1.5 40
h>1.5 80
(1) 若儿童身高h为输入值,相应的购票钱款为输出值,
则 1.0→________,1.3→_______,1.6→________;
(2) 若购票钱款为输入值,儿童身高 h 为输出值,则
0→__________,40→______________.
0
40
80
h≤1.2
1.2<h≤1.5
3. 判断下列对应是否为从 A 到 B 的函数:
(1) A={1,2,3,4,5},B={0,2,4,6,8},
对任意的 x∈A,x→2x;
解 x=5∈A,2x=10 B,故不是函数.
综上所述,结论是:
对应 x→2x 不是从A到B的函数.
(2) A= {1,2,3,4,5},B={x∣x<10,x∈N,对任
意的 x∈A,x→2x+1;
解:x=1∈A → 2x+1=3∈B;
x=2∈A → 2x+1=5∈B;
x=3∈A → 2x+1=7∈B;
x=4∈A → 2x+1=9∈B;满足函数的定义.
综上所述,结论是:对应 x→ 2x+1是从A到B的函数.
(3) A=B=N*,对任意的 x∈A,x→x-1;
解 x=1∈A,x-1=0 B,故不是函数.
综上所述,结论是:
对应x→x-1不是从A到B的函数.
(4) A为正实数集,B=R,对任意的 x∈A,x→x 的算
术平方根.
解 任一个正实数均对应唯一的算术平方根,且算术平方根在实数范围内,
即 >0,x∈A,则存在唯一实数∈R与之对应,满足函数的定义.
综上所述,结论是:对应 x → 是从A到B的函数.
4. 判断下列对应是否为函数:
(1) x→-x,x∈R;
(2) x→1,x∈R;
(3) x→y,其中 y=∣x∣,x∈R,y∈R;
(4) t→s,其中s=t,t∈R,s∈R;
(5) x→y,其中y=x,x∈ [0,+∞),y∈R;
(6) x→y,其中y为不大于的最大整数,x∈R,y∈Z.
是
是
是
是
不是
是
5. 已知函数f(x)=x-x2,求f(0),f(1),f(),f(n+1)-f(n).
解 ∵f(x) = x-x2;
∴f(0) = 0-02 = 0;
f(1) = 1-12 = 0;
f() = -()2 = - = ;
f(n+1) -f(n) =(n+1)-(n+1)2-(n-n2)
=n+1-n2-2n-1-n+n2
=-2n
6. 求下列函数的定义域:
(1) f(x)= 1-3x;
(2) f(x)= ;
解:R.
解 由 x2-1≠0,得 x≠±1,
∴函数f(x)的定义域为{x∣x≠±1 }.
(3) f(x) = + ;
2+x>0
解 由 得-2≤x≤1,
1-x≥0
∴函数f(x)的定义域为[-2,1].
(4) f(x) = +.
x+1≥0
解 由 得 x≥-1且 x≠0,
x≠0
∴函数f(x)的定义域为[-1,0) ∪(0,+∞).
7. 求下列函数的值域:
(1) f(x)=x2+x,x∈{l,2,3};
解 函数的定义域为{1,2,3},
∵ f(1)=12+1=2,f(2)=6,f(3)=12.
∴ 函数f(x)的值域为{2,6,12}.
(2) f(x)=(x-1)2-1;
解 函数的定义域为R,
∵ (x-1)2-1>-1,
∴函数f(x)的值域为[-1,+∞).
(3) f(x)=x+1,x∈(1,2].
解 ∵ x∈(1,2],
∴ x+l∈(2,3],
∴函数f(x)的值域为(2,3].
在初中,我们已学过函数的图象,并能作出函数 y=2x-1,y= (x≠0)以及 y=x2 的图象社会生活中还有许多函数图象的例子,如图所示的心电图、示波图等.
四、函数的图象
(1) 定义
将自变量的一个值x0作为_______,相应的___________作为纵坐标,就得到坐标平面上的一个点(x0,f(x0)).
当自变量取遍函数定义域A中的每一个值时,就得到一系列这样的点.所有这些点组成的图形就是函数 y=f(x)的图象.
横坐标
函数值f(x0)
(2) 集合表示:
所有这些点组成的集合(点集)为________________,
即_________________________.
(3)本质:函数对应的图形,即几何意义.
{(x,f(x)) ∣x∈A}
{(x,y) ∣y=f(x),x∈A}
所有这些点组成的图形就是函数 y=f(x) 的图象.
例如,初中学习过的 y= 的图象就是由点集 {(x,y) ∣y=,x≠0,x∈R}中元素(点) 组成的图形.
【思考】
集合{x∣y=f(x),x∈A}、{y∣y=f(x),x∈A} 能表示函数的图象吗 为什么
提示:不能. 上述两个集合都是数集,不是点集. 因此不能表示函数的图象.第一个集合表示函数的定义域,第二个集合表示函数的值域.
例 4
试画出下列函数的图象:
(1) f(x) = x+1;
(2) f(x) = (x-1)2+1,x∈[1,3).
解:描点作出图象,函数图象分别如图 5-1-4 和 5-1-5 所示.
函数 f(x)=(x-1)2+1, x∈[1,3) 的图象为函数g(x)=(x -1)2+1,x∈R 的图象上 x∈[1,3) 的一段. 其中,点(1,1) 在图象上,用实心点表示;而点(3,5)不在图象上,用空心点表示.
例 5
在 5.1节开头的第一个问题中,如果把人口数 y (百万)看作年份 x 的函数,试根据表 5-1-1,画出这个函数的图象.
解 由表5-1-1的数据,西出的函数图象是8个点,如图 5-1-6所示.
思 考
设函数 y=f(x) 的定义域为 A,集合 P= {(x,y)∣y= f(x). x∈A}与Q={y∣y=f(x), x∈A }相等吗 请说明理由.
例 6
试画出二次函数 f(x)=x2+1的图象,并根据图象回答下列问题:
(1) 比较 f(-2),f(1),f(3) 的大小;
(2)若0<x1<x2,试比较 f(x1)与f(x2)的大小.
解 函数图象如图 5-1-7.
(1) 比较 f(-2),f(1),f(3) 的大小;
解 根据图 5-1-7(1),容易发现
f(-2) =f(2),
f(1)<f(2)<f(3).
所以 f(1)<f(-2)<f(3).
(2) 若0<x1<x2,试比较 f(x1)与f(x2)的大小.
解 根据图 5-1-7(2),容易发现
当0<x1<x2 时,
f(x1) <f(x2).
思 考
在例 6(2)中,
(1) 如果把“0<x1<x2”改为“x1<x2<0”,那么 f(x1)与f(x2)哪个大
(2) 如果把“0<x1<x2”改为“∣x1∣<∣x2∣”,那么 f(x1) 与 f(x2) 哪个大
请结合图象回答上述两个问题,并用不等式的基本知识来解决例 6及上述思考中的问题.
信息技术
下面我们介绍在 Excel 工作表中用“描点连线”的方法绘制函数 f(x)=(x-1)2+1的图象,不妨作 x∈[-2,2]上的图象.
(1)第一列产生自变量的值:在单元格 A1,A2 内分别输入-2,-1.9,选中这两个单元格后,按住鼠标左键并向下方拖曳“填充柄”,如图 5-1-8,直到单元格内出现填充值 2 时为止.
(2) 第二列产生对应的函数值: 如图 5-1-9,在 B1 内输入“=(A1-1)^2+1”,敲回车键或在编辑栏内选中“√”,拖曳 B1 的填充柄至所需的单元格(或双击 B1 的填充柄),得到与第一列相对应的函数值.
(3) 成图:光标置于数据区的任一位置,插入“图表”,选择“XY散点图/无数据点平滑线散点图”,点击“完成”,便得函数 f(x) =(x-1)2+1在区间[-2,2 ]上的图象,如图 5-1-10.
你能用上面的方法绘制函数 f(x)=x3的图象吗
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 已知函数 y=f(x),x∈A,若x0 A,则点(x0,f(x0))一定不在函数的图象上. ( )
(2)直线 x=a 和函数 y=f(x),x∈[m,n]的图象有1个交点. ( )
(3) 函数的图象一定是连续的. ( )
2. (多选题)下列坐标系中的曲线或直线,能作为函数
y=f(x)的图象的有 ( )
BD
解析:能作为函数的图象,必须符合函数的定义,即定义域内的每一个x只能有唯一的y与x对应,故BD可以,AC不可以.
解析
3. 函数 y=x+1,x∈Z,且∣x∣<2的图象是________.
(填序号)
③
解析:由题意知,函数的定义域是{-1,0,1},值域是{0,1,2},函数的图象是三个点,故③正确.
解析
【课堂检测·素养达标】
1. 函数 y=x0 的图象是 ( )
B
解析
解析:因为函数 y=x0的定义域为{x|x≠0},所以排除A,C. 又 y=x0=1,所以排除D.
2. 函数 y= 的大致图象只能是 ( )
B
解析
解析:函数 y= 的大致图象由 y= 的图象向左平移2个单位得到.
解析:因为二次函数的图象过(4,0),
所以16a+4b+c=0.①又过点(0,2),所以c = 2.②
由顶点坐标为(4,0)可知 x=-=4.③
由①②③可解得 a=,b=-1,c=2,所以 abc=-.
3. 二次函数f(x) =ax2+bx+c的图象的顶点为(4,0),且过点(0,2),则abc等于 ( )
A. -6 B.11 C. - D.
C
解析
4. 若函数y=f(x)的图象经过点(0,1),那么函数y=f(x+4)
的图象经过点___________.
(-4,1)
解析
解析:y=f(x+4) 可以认为把 y=f(x) 向左移了4个单位,由 y=f(x) 经过点(0,1),易知 f(x+4) 经过点(-4,1).
练 习
1. 画出下列函数的图象:
(1) f(x)=2x-1;
(2) f(x)=2x-1,x∈ [-1,2);
(3) f(x)=,x∈(0,+∞);
(4) f(x) = +1,x∈(0, +∞);
(5) f(x) = x2,x∈[-1,2];
(6) f(x)=(x-1)2,x∈[0,3].
2. 先画出下列函数的图象,再求出每个函数的值域:
(1) f(x)=(x-1)2,x∈{- 1,0,1,2};
解 由定义域为{- 1,0,1,2}知,
其函数图象就是四个点:
A(-1,4),B(0,1),C(1,0),D(2,1),图象如图所示.
其值域为{4,1,0}.
(2) f(x)=x2,x∈[1,2);
解 函数 f(x)=x2,x∈[1,2) 的图象是抛物线 x2=y落在第一象限内的一部分,其图象如图所示.
函数 f(x)=x2,x∈[1,2)为增函数,
故值域为[f(1),f(2))=[1,4)
(3) f(x)=,x∈[1, 3);
解 ∵x∈[1,3),f(x)=,
∴ 其图象落在第一象限,且是反比例函数 f(x)=图象的一部分.
图象如图所示.
函数 f(x)=,x∈[1,3) 为减函数,
故其值域为(f(3),f(1)] = (,1]
(4) f(x)= ,x为正实数.
解 ∵x>0,故f(x)=>0,其图象在第一象限内,
它是抛物线 y2=x (x>0,y>0) 在第一象限内的部分.
其图象如图所示.
函数f(x)=,x>0 为增函数,
故值域为(f(0),+∞)=(0,+∞ )
3. 根据如图所示的函数 y=f(x) 的图象填空:
(1) f(0)=_______,f(1)= _______,
f(2) =_______.
(2) 若-1<x1<x2<1,则f(x1)与 f(x2)
的大小关系是___________.
2
3
0
f(x1)< f(x2)
习题 5.1
感受·理解
1. 已知函数 y=5x-2.
(1) 当x=0,1,5时,分别求出y的值;
解 ∵函数 y=5x-2,
∴当x=0时,y=5×0-2=-2;
当x=1时,y=5×1-2=3;
当x=5时,y=5×5-2=23;
(2) 当y=0,1,5时,分别求出x的值.
解 令5x-2=0,解得 x=,∴当y=0时,x=;
令5x-2=1,解得 x=,∴当y=1时, x=;
令5x-2=5,解得 x=,∴当y=5时, x=.
2. 判断下列对应 f 是否为从集合 A 到集合 B 的函数:
(1) A={,1,};B ={-6,-3,1},f()=-6,
f(1)= -3,f()=1;
满足函数的定义,则f为从集合A到集合B的函数.
(2) A={1,2,3},B={7,8,9},f(1)=f(2)=7,
f(3)=8;
满足函数的定义,f是从集合A到集合B的函数.
(3) A=B={1,2,3},f(x) = 2x-1;
∵f(2)=5,不满足条件.
故f不是从集合A到集合B的函数;
(4) A=B={ x∣x ≥ -1},f(x)=2x+1;
满足函数的定义,则f是从集合A到集合B的函数;
(5) A=Z,B={-1,1},n为奇数时,f(n)=-1;
n为偶数时,f(n) = 1.
满足函数的定义,则f是从集合A到集合B的函数.
3. 求下列函数的定义域、值域,并画出图象:
(1) f(x)=3x;
解 函数 f(x)=3x 定义域为R,值域为R,图象如下:
(2) f(x)=-3x+1;
解 函数 f(x)=-3x+1定义域为R,值域为R,图象如下:
(3) f(x)= -;
解 定义域为(-∞,0)∪(0,+∞),
值域为 (-∞,0)∪(0,+∞),
图象如下:
(4) f(x)= -+1;
解 定义域为(-∞,0)∪(0,+∞),
值域为 (-∞,1)∪(1,+∞),
图象如下:
(5) f(x)=1-x2;
解 定义域为R,
值域为 (-∞,1],
图象如下:
(6) f(x) =x2+2x.
解 定义域为R,
值域为[-1,+∞),
图象如下:
4. 判断下列各组函数是否是同一个函数,并说明理由:
(1) y=x,y=;
解 不是.
∵y=x 的定义域为R,
而y=的定义域为{x∣x≠0},
∴这两个函数的定义域不同.
(2) y=x2,y=x2,x∈[0,+∞);
解 不是.
因为两个函数的定义域不同
(3) y=x,s=t;
解 是.
虽然两个函数的变量不同,
但定义域都是 R,对应关系也相同.
(4) f(x)=1,g(x)=1.
解 是.
因为两个函数的定义域相同,
对应关系也相同.
思考·运用
5. 已知函数 f(x) = ax+b,且 f(3) = 7,f(5) =-1,
求 f(0),f(1) 的值.
解 ∵ f(x)=ax+b,且 f(3)=7,f(5)=-1,
3a+6=7
∴ ,解得a=-4,b=19.
5a+b=-1
则 f(x) =-4x+19,则 f(0) =19,
f(1) = - 4+19=15.
6. 直线x=a和函数y=x2+1的图象的公共点可能有几个
解 由函数的定义知
直线 x=a和函数 y=a+1的图象有且仅有一个公共点.
7. 已知f(t)=,g(t)=,求证:f(t)-g(t)=-2g(t2).
证明:∵ f(t)= ,g(t)=,
∴ f(t)-g(t)= -
=
= = -2g(t2).
8. 如果函数 f(x)与 g(x)分别由下表给出,那么
f(f(1))=__________,f(g(2))=__________,
g(f(3))=__________,g(g(4))=__________.
x 1 2 3 4
f(x) 2 3 4 1
x 1 2 3 4
g(x) 2 1 4 3
3
2
3
4
9. 设函数 f(x)=2x+3,函数 g(x)=3x-5,
求 f(g(x)),g(f(x)).
解 ∵f(x)=2x+3,g(x)=3x-5,
∴f(g(x))=2g(x)+3=2(3x-5)+3=6x-7,
g(f(x))=3f(x)-5=3(2x+3)-5=6x+4.
探究·拓展
10. 已知集合 A=R,B={-1,1},对应关系 f 如下:
当x为有理数时,f(x)=-l;
当x为无理数时,f(x)=1.
该对应是从集合 A 到集合 B 的函数吗
解 ∵A=R,B={-1,1}都是非空数集,
且对于集合A中的任意一个数x,在对应关系f的作用下,
在集合B中都有唯一的一个确定的数f(x)与之对应,
故该对应是从集合A到集合B的一个函数.
11. (操作题)将一枚子投掷 10 次,并将每次子向上的点数
记录在下表中规定对应关系f:对每一投掷序号 n(n=
1,2,···,10) 对应到这次子的向上点数. 试判断对
应 f 是否为函数. 若是,这个函数值域一定是集合{1,
2,3,4,5,6}吗
投掷序号 1 2 3 4 5 6 7 8 9 10
向上点数 3 2 3 6 4 5 3 2 4 5
∵对于任意一个序号n都有唯一的数与之对应,
∴对应f是函数因为在函数值中,集合{1,2,3,4,5,6}中的数并不一定每个都出现,
由上表可以看出,此函数的值域为{2,3,4,5,6},
∴ 这个函数的值域不一定是{1,2,3,4,5,6}.
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
