5.2 函数的表示方法 2023-2024学年高一数学苏教版(2019)必修第一册 课件(共71张PPT)
文档属性
| 名称 | 5.2 函数的表示方法 2023-2024学年高一数学苏教版(2019)必修第一册 课件(共71张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 64.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 21:37:00 | ||
图片预览










文档简介
(共71张PPT)
第5章
函数概念与性质
5 . 2
函数的表示方法
让我们再来看 5.1节开头的 3个函数问题.
● 这3个函数是怎样表示的
在第一个问题中,只要知道了表 5-1-1中的某个年份,就能从此表中查得相应的人口数. 这种用列表来表示两个变量之间函数关系的方法称为列表法.
在第二个问题中,物体下落时间 x 与下落距离 y 的函数关系为 y=4.9x2(x≥0). 这种用等式来表示两个变量之间函数关系的方法称为解析法. 这个等式通常叫作函数的解析表达式,简称解析式.
在第三个问题中,我们用图象表示了时刻与气温的关系. 这种用图象表示两个变量之间函数关系的方法称为图象法.
一、表示函数的三种方法
解析法 用_____来表示两个变量之间的函数关系
列表法 用_____来表示两个变量之间的函数关系
图象法 用_____表示两个变量之间的函数关系
等式
列表
图象
二、本质
两个变量对应关系的三种不同方式的表示.
【思考】
函数的三种表示方法各有哪些优缺点
表示 方法 优点 缺点
列表法 不需要计算就可以直接看出与自变量对应的函数值 只能表示自变量可以一一列出的函数关系
表示 方法 优点 缺点
图象法 能从整体上形象直观地表示出函数的变换情况 只能近似地求出函数值,而且有时误差较大
解析法 便于用解析式研究函数的性质 不够形象、直观,而且并不是所有的函数都能用解析法表示出来
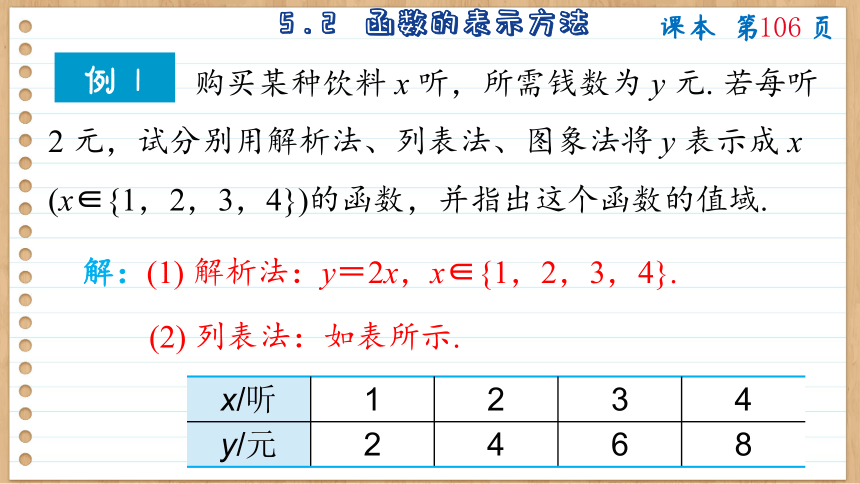
例 1
购买某种饮料 x 听,所需钱数为 y 元. 若每听 2 元,试分别用解析法、列表法、图象法将 y 表示成 x (x∈{1,2,3,4})的函数,并指出这个函数的值域.
解:(1) 解析法:y=2x,x∈{1,2,3,4}.
(2) 列表法:如表所示.
x/听 1 2 3 4
y/元 2 4 6 8
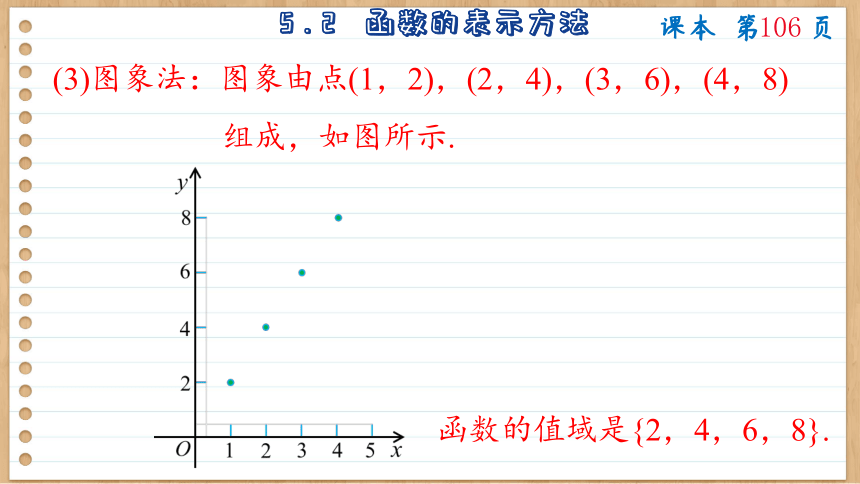
(3)图象法:图象由点(1,2),(2,4),(3,6),(4,8)
组成,如图所示.
函数的值域是{2,4,6,8}.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 任何一个函数都可以用图象法表示出来. ( )
(2) 任何一个函数都可以用解析法表示出来. ( )
(3) 函数的图象一定是连续不断的曲线. ( )
2. 已知函数 f(x) 的图象如图所示,其中点 A,B 的坐标分别为(0,3),(3,0),则 f(f(0))=( )
A.2 B.4 C.0 D.3
C
解析:结合题图可得 f(0)=3,则 f(f(0))=f(3)=0.
解析
3. 某商场新进了10台彩电,每台售价 3 000元,试求售出台数 x ( x 为正整数)与收款数 y 之间的函数关系,用解析法表示 y=_______________________________.
3 000x,x∈{1,2,3,…,10}
解析:用解析法表示 y=3 000x,x∈{1,2,3,…,10}.
解析
【课堂检测·素养达标】
1.如图是反映某市某一天的温度随时间变化情况的图象.由图象可知,下列说法中错误的是 ( )
A.这天15时的温度最高
B.这天3时的温度最低
C.这天的最高温度与最低温度相差13℃
D.这天21时的温度是30℃
C
解析:这天的最高温度与最低温度相差为 36-22=14(℃).
解析
2. 已知函数 f(x) 满足:f() =8x2-2x-1,则 f(x)= ( )
A. 2x4+3x2 B.2x4-3x2
C. 4x4+x2 D.4x4-x2
A
解析:令 t= ,t≥0,得 x=,
故有 f(t)=8× -2× -1,
整理得 f(t)=2t4+3t2,即 f(x)=2x4+3x2,x≥0.
解析
3. 已知函数 f(x)=x-,且此函数的图象过点(5,4),
则实数 m 的值为__________.
5
解析:因为函数 f(x)=x- 的图象过点(5,4),
所以 4=5-,解得 m=5.
解析
4. 已知一次函数 f(x) 满足条件f(x+1)+f(x) =2x,则函数
f(x)的解析式为f(x) =____________.
x-
解析
解析:设 f(x)=kx+b,k≠0,
因为f(x+1)+f(x) =2x,所以k(x+1)+b+kx+b=2x,
即 2kx+k+2b=2x,所以
解可得,k=1,b=-,
所以 f(x)=x- .
2k=2,
k+2b=0.
5. 作出下列函数的图象,并求其值域:
(1) y=1-x (x∈Z,且∣x∣≤2).
解 因为x∈Z,且∣x∣≤2,所以 x∈{-2,-1,0,1,2},
所以该函数图象为直线 y=1-x 上的孤立点.
由图象知,y∈{-1,0,1,2,3}.
(2) y=2x2-4x-3 (0≤x<3).
解 因为 y=2(x-1)2-5,
所以当x=0时,y=-3;
当x=3时,y=3;
当x=1时,y=-5.
因为x∈[0,3),故图象是一段抛物线.
由图象可知,y∈[-5,3).
画出函数 f(x) =∣x∣的图象,并求 f(-3),f(3),f(-1),f(1) 的值.
例 2
-x,x<0,
解:因为 f(x) =∣x∣=
x, x≥0,
所以函数 f(x)的图象为过原点且平分第一象限、第二象限的一条折线,
如图所示. 其中,
f(-3)=3,f(3)=3,f(-1)=1,f(1)=1.
某市出租汽车收费标准如下:在 3 km 以内(含 3 km) 路程按起步价9元收费,超过3 km 的路程按 24元/km 收费试写出收费额(单位:元)关于路程(单位:km)的函数解析式.
例 3
解 设路程为 x km 时,收费额为 y 元,则由题意得:当x≤3时,y=9;当x>3时,按 2.4 元/km 所收费用为 2.4×(x-3),那么有 y=9+2.4×(x-3).
于是,收费额关于路程的函数解析式为
9, 0<x≤3,
y=
9+2.4×(x-3), x>3,
9, 0<x≤3,
即 y=
2.4x+1.8, x>3.
三、分段函数
(1)定义:
在定义域内不同部分上,有不同的解析表达式,像这样的函数叫作分段函数.
(2)本质:函数在定义域的不同的范围内,有着不同的对应关系.
(3) 应用:可以用分段函数描述很多生活中的实际问题.
【思考】
提示:分段函数是一个函数,只不过在不同范围上解析式不同.
1. 分段函数 y= 是两个函数吗
-x,x<0,
x,x≥0.
2. 分段函数的定义域、值域是怎么规定的
提示:定义域为各段范围的并集;
值域为各段上值域的并集.
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 分段函数中各段函数的定义域交集是空集,并集是分段函数的定义域. ( )
(2) 函数 y=|x+1| 不是分段函数. ( )
(3) 分段函数 f(x)= 则f(-2)=-2. ( )
x,x≥0,
2x,x<0.
【基础小测】
2. 若 f(x)= 则f(f(-2))= ( )
A. 2 B. 3 C. 4 D.5
x2,(x≥0),
-x,(x<0).
C
解析:因为-2<0,所以f(-2) =- (-2) =2,
又因为2>0,所以f(f(-2)) =f(2) =22=4.
解析
3. 某城市出租车起步价为10元,最长可租乘 3 km (含3 km),以后每1 km为1.6元(不足1 km,按1 km计费),若出租车行驶在不需等待的公路上,则出租车的费用y(元)与行驶的里程x(km)之间的函数图象大致为 ( )
C
【课堂检测·素养达标】
1.一列货运火车从某站出发,匀加速行驶一段时间后开始匀速行驶,过了一段时间,火车到达下一站停车,装完货以后,火车又匀加速行驶,一段时间后再次匀速行驶,下列图象可以近似地刻画出这列火车的速度变化情况的是 ( )
解析:根据题意,知这列火车从静止开始匀加速行驶,所以排除A,D;然后匀速行驶一段时间后又停止了一段时间,排除C.
解析
2. 已知函数 f(x)= 则f(2)=( ).
A. -1 B.0 C.1 D.2
x-2,x<2,
f(x-1),x≥0.
解析:f(2)=f(2-1)=f(1)=1-2=-1.
解析
A
3. 国家规定个人稿费纳税办法:不超过800元的不纳税;超过800元而不超过4 000元的按超过800元部分的14%纳税;超过4 000元的按全部稿酬的11.2%纳税.已知某人出版一本书,共纳税420元,则这个人应得稿费(扣税前)为 ( )
A.2 800元 B.3 000元 C.3 800元 D.3 818元
C
4. 已知函数 f(x) = 若f(x)=3,
则 x=___________.
x+2,x≤0,
x2,0<x≤0.
解析:依题意,若 x≤0,则 x+2=3,解得 x=1,
不合题意,舍去;
若 0<x≤3,则 x2=3,
解得 x=- (舍去) 或 x= .
解析
5. 已知函数 f(x) 的图象是两条线段(如图所
示,不含端点),则f(f())=______.
解析
解析:由题图可知,函数f(x)的解析式为
f(x)=
所以 f()=-1=- .
所以 f(f())=f(-) =-+1= .
x-2,0<x<1,
x+1,-1<x<0.
练 习
1. 1 n mile (海里) 约合 1852 m,根据这一关系,写出米
数 y 关于海里数 x 的函数解析式.
解 由题意得 y=1852x (x≥0),
∴ 米数 y关于海里数 x 的函数解析式为:
y=1852x (x≥0)
2. 画出雨数 f(x)=∣x+3∣的图象.
解 当x+3>0,即 x>-3时,f(x)=∣x+3∣=x+3,
当x+3<0,即 x<-3时,f(x)=∣x+3∣=-x-3.
∴ f(x)=
函数 f(x)=∣x+3∣的图象如图所示.
x+3 ,x≥-3,
-x-3,x<-3.
3. (1)用长为 30 cm的铁丝围成矩形,试将矩形面积 S (单
位:cm2) 表示为矩形一边长 x (单位:cm) 的函数,
并画出函数的图象;
解 由题意可知
S=
=x(15-x)
=-x2 +15x,(0<x<15).
(2) 用细铁丝围一个面积为 1 cm2 的矩形,试将所用铁丝
的长度 l (单位:cm) 表示为矩形的某条边长 x (单位:
cm) 的函数.
解 设矩形的某一条边长为x(cm),
则 x>0,另一条边长为(cm),
所以铁丝的长度 l=2x+,x>0.
4. 下列图象中,表示函数关系 y=f(x) 的有________.
(1)(4)
习题 5.2
感受·理解
1. 物体从静止开始下落,下落的距离与下落时间的平方
成正比. 已知开始下落的 2s 内,物体下落了 19.6,求
开始下落的 3s 内物体下落的距离.
解 由题意设下落的距离y与时间t满足 y=kt2(k≠0),
由已知可得当 t=2 时,y=19.6,
故19.6=4k,解得 k=4.9,
所以 y= 4.9t2
所以当t=3时,y=4.9×32= 44.1.
所以开始下落的3s内物体下落的距离是44.1m.
2. 某公司将进一批单价为 8 元的商品,若按 10 元/个销售,每天可卖出100个;假设销售价每上涨 1 元/个,每天的销售量就减少 10 个.
(1) 设商品的销售价上涨 x 元/个(0≤x≤10,x∈N),每天的利润为 y 元,试用列表法表示函数 y=f(x);
(2) 求销售价为 13 元/个时每天的销售利润;
(3) 如果销售利润为 360 元,那么销售价上涨了多少元
(1) 设商品的销售价上涨 x 元/个(0≤x≤10,x∈N),每
天的利润为 y 元,试用列表法表示函数 y=f(x);
解 y=(10+x-8)(100-10x)
=-10x2+80x+200;
即 y=-10x2+80x+200;
(2) 求销售价为 13 元/个时每天的销售利润;
解 销售价为13元/个时,上涨价3,则每天的销售利润为:
-10×32+80×3+200=350(元);
(3) 如果销售利润为 360 元,那么销售价上涨了多少元
解 销售利润为360元,即 y= 360,
则: -10x2+80x+200=360;
解得 x=4;
即销售价上涨了4元.
3. 设距地面高度 x (单位:km)的气温为 y (单位:℃),在距地面高度不超过11 km时,y 随着 x 的增加而降低,且每升高 1 km,大气温度降低 6 ℃;高度超过 11km 时,气温可视为不变. 设地面气温为22℃,试写出 y=f(x) 的解析式,并分别求高度为 3.5 km 和 12 km 的气温.
y=
22-6x,0 ≤x≤11,
-44,x>11.
f(3.5)= 22-6×3.5=1,
f(12) = - 44.
即高度为 3.5 km 时的气温为1℃,
高度为12 km 时的气温为- 44℃.
4. 建造一个容积为 8 m深为 2 m 的长方体形状的无盖水池,已知池底和池壁的造价分别为 120 元/m2 和 80 元/m2,求总造价 y (单位:元) 关于底面一边长 x (单位:m) 的函数解析式,并指出该函数的定义域.
解 底面一边长为,则另一边长为.
池底的造价为固定值 120×4=480(元),
池壁的造价为变化值
80 ×(2x +2· ) ×2 =320x + ,
则 y= 480+320x+,
定义域为 x∈(0,+∞)
5. 画出函数 f(x) =-x2+x+1(-1≤x≤1) 的图象,并根据图象回答下列问题:
(1)当-1≤x1<x2≤时,比较f(x1)与 f(x2)的大小;
(2) 是否存在 x0∈[-1,1],使得 f(x0)=-2
作出函数 f(x)=-x2+x+1(-1≤x≤1)的图象如下图:
图象为开口向下,且对称轴为x=的抛物线的一段.
(1)当-1≤x1<x2≤时,比较f(x1)与 f(x2)的大小;
解 由图象可知:函数 f(x) 在[-1,]
上是增函数,
∴ -1≤x1<x2≤,
有f(x1) < f(x2);
(2) 是否存在 x0∈[-1,1],使得 f(x0)=-2
解 由图象可知:
当x∈[-1,1] 时,
fmin (x) =f(-1) = -1,
fmax (x) =f() = ,即f(x)∈[-1, ],
∴ 不存在 x0∈[-1,1],使得 f(x0)=-2.
6. 已知A ={1,2,3,4},B = {1,3,5},试写出从
A到B的两个函数.
解 f(x)=x0;g(x)=
1,x=1,2,
3,x=3,4.
(答案不唯一)
7. 已知函数 f(x)= 求 f(2),f(f(-2))的值.
x, x≥0,
x2,x<0,
解 f(2)=2,
f(f(-2))=f(4)=4.
8. 画出函数 y=x3(x∈{-2,-1.5,-1,-0.5,0,0.5,
1,1.5,2})的图象.
思考·运用
9. 某人去上班,先跑步,后步行. 如果 y 表示该人离单位的距离,x 表示出发后的时间,那么下列图象中符合此人走法的是 ( ).
D
10. 请写出 3 个不同的函数 y=f(x) 的解析式满 f(1)=1,
f(2)=4.
解:f(x)=x2;
f(x)=3x-2;
f(x)=2x2-3x+2.(答案不唯一)
11.已知某皮鞋厂一天的生产成本 C (单位:元)与生产数量 n (单位:双)之间的函数关系式是 C=4000 + 50n.
(1)求一天生产1000 双皮鞋的成本;
(2) 如果某天的生产成本是 48 000 元,那么这一天生产了多少双皮鞋
(3) 若每双皮鞋的售价为 90 元,且生产的皮鞋全部售出,试写出这一天的利润 P 关于这一天生产数量 n 的函数关系式,并求出每天至少生产多少双皮鞋,才能不亏本.
(1) 求一天生产1000 双皮鞋的成本;
解 ∵生产成本C(元) 与生产数量n (双) 之间的函数关系是C=4000+50n.
∴n=1000时,C=4000+ 50000=54000;
(2) 如果某天的生产成本是 48 000 元,那么这一天生产了多少双皮鞋
解 令 C=4000+50n=48000,
解得 n=880;
(3) 若每双皮鞋的售价为 90 元,且生产的皮鞋全部售出,试写出这一天的利润 P 关于这一天生产数量 n 的函数关系式,并求出每天至少生产多少双皮鞋,才能不亏本.
解 由题意得:某皮鞋厂一天的生产成本C(元) 与生产数量n(双)之间的函数关系是C=4000+50n.
∴p(n)=90n-(4000+50n)=40n-4000(n∈N+)
要不亏本,必须p(n) >0,解得 n≥100.
即每天至少生产100双皮鞋,才能不亏本.
12. 从2006 年11月15日起国内投首重100g以内的外信的邮资标准是每封信的质量不超过 20g 付邮资 120 分,超过20g 而不超过 40g 付邮资 240分,超过 40g 而不超过 60g 付邮资 360分,依此类推试画出反映每封不超过 90g 的信函应付邮资 y (单位:分)与信函的质量 x (单位:g)之间的函数关系的图象.
解:由题意,得 y=
120,x∈(0,20],
240,x∈(20,40],
360,x∈(40,60],
480,x∈(60,80],
600,x∈(80,90].
图象如图所示.
y/分
x/g
600
480
360
240
120
20
40
60
80
100
O
探究·拓展
13. (开放题) 已知一个函数的解析式为 y=x2,它的值域为区间[1,4],这样的函数有多少个 试写出其中两个函数.
解 设 y=f(x)=x2,
其图象是开口向上的抛物线,其对称轴方程为x=0,是偶函数,
f(x) 在(0,+∞ ) 上单调递增,在(-∞,0) 上单调递减,
要使 y∈[1,4],
故只需确定函数的定义域即可.
当 y=4时,x=±2,当y=1时,x=±1,
这样的函数有无数个,
比如 y=x2,x∈[1,2] ∪{-1},
比如 y=x2,x∈[1,2] ∪{-2}.
本课结束
This lesson is over
THANKS!
第5章
函数概念与性质
5 . 2
函数的表示方法
让我们再来看 5.1节开头的 3个函数问题.
● 这3个函数是怎样表示的
在第一个问题中,只要知道了表 5-1-1中的某个年份,就能从此表中查得相应的人口数. 这种用列表来表示两个变量之间函数关系的方法称为列表法.
在第二个问题中,物体下落时间 x 与下落距离 y 的函数关系为 y=4.9x2(x≥0). 这种用等式来表示两个变量之间函数关系的方法称为解析法. 这个等式通常叫作函数的解析表达式,简称解析式.
在第三个问题中,我们用图象表示了时刻与气温的关系. 这种用图象表示两个变量之间函数关系的方法称为图象法.
一、表示函数的三种方法
解析法 用_____来表示两个变量之间的函数关系
列表法 用_____来表示两个变量之间的函数关系
图象法 用_____表示两个变量之间的函数关系
等式
列表
图象
二、本质
两个变量对应关系的三种不同方式的表示.
【思考】
函数的三种表示方法各有哪些优缺点
表示 方法 优点 缺点
列表法 不需要计算就可以直接看出与自变量对应的函数值 只能表示自变量可以一一列出的函数关系
表示 方法 优点 缺点
图象法 能从整体上形象直观地表示出函数的变换情况 只能近似地求出函数值,而且有时误差较大
解析法 便于用解析式研究函数的性质 不够形象、直观,而且并不是所有的函数都能用解析法表示出来
例 1
购买某种饮料 x 听,所需钱数为 y 元. 若每听 2 元,试分别用解析法、列表法、图象法将 y 表示成 x (x∈{1,2,3,4})的函数,并指出这个函数的值域.
解:(1) 解析法:y=2x,x∈{1,2,3,4}.
(2) 列表法:如表所示.
x/听 1 2 3 4
y/元 2 4 6 8
(3)图象法:图象由点(1,2),(2,4),(3,6),(4,8)
组成,如图所示.
函数的值域是{2,4,6,8}.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 任何一个函数都可以用图象法表示出来. ( )
(2) 任何一个函数都可以用解析法表示出来. ( )
(3) 函数的图象一定是连续不断的曲线. ( )
2. 已知函数 f(x) 的图象如图所示,其中点 A,B 的坐标分别为(0,3),(3,0),则 f(f(0))=( )
A.2 B.4 C.0 D.3
C
解析:结合题图可得 f(0)=3,则 f(f(0))=f(3)=0.
解析
3. 某商场新进了10台彩电,每台售价 3 000元,试求售出台数 x ( x 为正整数)与收款数 y 之间的函数关系,用解析法表示 y=_______________________________.
3 000x,x∈{1,2,3,…,10}
解析:用解析法表示 y=3 000x,x∈{1,2,3,…,10}.
解析
【课堂检测·素养达标】
1.如图是反映某市某一天的温度随时间变化情况的图象.由图象可知,下列说法中错误的是 ( )
A.这天15时的温度最高
B.这天3时的温度最低
C.这天的最高温度与最低温度相差13℃
D.这天21时的温度是30℃
C
解析:这天的最高温度与最低温度相差为 36-22=14(℃).
解析
2. 已知函数 f(x) 满足:f() =8x2-2x-1,则 f(x)= ( )
A. 2x4+3x2 B.2x4-3x2
C. 4x4+x2 D.4x4-x2
A
解析:令 t= ,t≥0,得 x=,
故有 f(t)=8× -2× -1,
整理得 f(t)=2t4+3t2,即 f(x)=2x4+3x2,x≥0.
解析
3. 已知函数 f(x)=x-,且此函数的图象过点(5,4),
则实数 m 的值为__________.
5
解析:因为函数 f(x)=x- 的图象过点(5,4),
所以 4=5-,解得 m=5.
解析
4. 已知一次函数 f(x) 满足条件f(x+1)+f(x) =2x,则函数
f(x)的解析式为f(x) =____________.
x-
解析
解析:设 f(x)=kx+b,k≠0,
因为f(x+1)+f(x) =2x,所以k(x+1)+b+kx+b=2x,
即 2kx+k+2b=2x,所以
解可得,k=1,b=-,
所以 f(x)=x- .
2k=2,
k+2b=0.
5. 作出下列函数的图象,并求其值域:
(1) y=1-x (x∈Z,且∣x∣≤2).
解 因为x∈Z,且∣x∣≤2,所以 x∈{-2,-1,0,1,2},
所以该函数图象为直线 y=1-x 上的孤立点.
由图象知,y∈{-1,0,1,2,3}.
(2) y=2x2-4x-3 (0≤x<3).
解 因为 y=2(x-1)2-5,
所以当x=0时,y=-3;
当x=3时,y=3;
当x=1时,y=-5.
因为x∈[0,3),故图象是一段抛物线.
由图象可知,y∈[-5,3).
画出函数 f(x) =∣x∣的图象,并求 f(-3),f(3),f(-1),f(1) 的值.
例 2
-x,x<0,
解:因为 f(x) =∣x∣=
x, x≥0,
所以函数 f(x)的图象为过原点且平分第一象限、第二象限的一条折线,
如图所示. 其中,
f(-3)=3,f(3)=3,f(-1)=1,f(1)=1.
某市出租汽车收费标准如下:在 3 km 以内(含 3 km) 路程按起步价9元收费,超过3 km 的路程按 24元/km 收费试写出收费额(单位:元)关于路程(单位:km)的函数解析式.
例 3
解 设路程为 x km 时,收费额为 y 元,则由题意得:当x≤3时,y=9;当x>3时,按 2.4 元/km 所收费用为 2.4×(x-3),那么有 y=9+2.4×(x-3).
于是,收费额关于路程的函数解析式为
9, 0<x≤3,
y=
9+2.4×(x-3), x>3,
9, 0<x≤3,
即 y=
2.4x+1.8, x>3.
三、分段函数
(1)定义:
在定义域内不同部分上,有不同的解析表达式,像这样的函数叫作分段函数.
(2)本质:函数在定义域的不同的范围内,有着不同的对应关系.
(3) 应用:可以用分段函数描述很多生活中的实际问题.
【思考】
提示:分段函数是一个函数,只不过在不同范围上解析式不同.
1. 分段函数 y= 是两个函数吗
-x,x<0,
x,x≥0.
2. 分段函数的定义域、值域是怎么规定的
提示:定义域为各段范围的并集;
值域为各段上值域的并集.
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 分段函数中各段函数的定义域交集是空集,并集是分段函数的定义域. ( )
(2) 函数 y=|x+1| 不是分段函数. ( )
(3) 分段函数 f(x)= 则f(-2)=-2. ( )
x,x≥0,
2x,x<0.
【基础小测】
2. 若 f(x)= 则f(f(-2))= ( )
A. 2 B. 3 C. 4 D.5
x2,(x≥0),
-x,(x<0).
C
解析:因为-2<0,所以f(-2) =- (-2) =2,
又因为2>0,所以f(f(-2)) =f(2) =22=4.
解析
3. 某城市出租车起步价为10元,最长可租乘 3 km (含3 km),以后每1 km为1.6元(不足1 km,按1 km计费),若出租车行驶在不需等待的公路上,则出租车的费用y(元)与行驶的里程x(km)之间的函数图象大致为 ( )
C
【课堂检测·素养达标】
1.一列货运火车从某站出发,匀加速行驶一段时间后开始匀速行驶,过了一段时间,火车到达下一站停车,装完货以后,火车又匀加速行驶,一段时间后再次匀速行驶,下列图象可以近似地刻画出这列火车的速度变化情况的是 ( )
解析:根据题意,知这列火车从静止开始匀加速行驶,所以排除A,D;然后匀速行驶一段时间后又停止了一段时间,排除C.
解析
2. 已知函数 f(x)= 则f(2)=( ).
A. -1 B.0 C.1 D.2
x-2,x<2,
f(x-1),x≥0.
解析:f(2)=f(2-1)=f(1)=1-2=-1.
解析
A
3. 国家规定个人稿费纳税办法:不超过800元的不纳税;超过800元而不超过4 000元的按超过800元部分的14%纳税;超过4 000元的按全部稿酬的11.2%纳税.已知某人出版一本书,共纳税420元,则这个人应得稿费(扣税前)为 ( )
A.2 800元 B.3 000元 C.3 800元 D.3 818元
C
4. 已知函数 f(x) = 若f(x)=3,
则 x=___________.
x+2,x≤0,
x2,0<x≤0.
解析:依题意,若 x≤0,则 x+2=3,解得 x=1,
不合题意,舍去;
若 0<x≤3,则 x2=3,
解得 x=- (舍去) 或 x= .
解析
5. 已知函数 f(x) 的图象是两条线段(如图所
示,不含端点),则f(f())=______.
解析
解析:由题图可知,函数f(x)的解析式为
f(x)=
所以 f()=-1=- .
所以 f(f())=f(-) =-+1= .
x-2,0<x<1,
x+1,-1<x<0.
练 习
1. 1 n mile (海里) 约合 1852 m,根据这一关系,写出米
数 y 关于海里数 x 的函数解析式.
解 由题意得 y=1852x (x≥0),
∴ 米数 y关于海里数 x 的函数解析式为:
y=1852x (x≥0)
2. 画出雨数 f(x)=∣x+3∣的图象.
解 当x+3>0,即 x>-3时,f(x)=∣x+3∣=x+3,
当x+3<0,即 x<-3时,f(x)=∣x+3∣=-x-3.
∴ f(x)=
函数 f(x)=∣x+3∣的图象如图所示.
x+3 ,x≥-3,
-x-3,x<-3.
3. (1)用长为 30 cm的铁丝围成矩形,试将矩形面积 S (单
位:cm2) 表示为矩形一边长 x (单位:cm) 的函数,
并画出函数的图象;
解 由题意可知
S=
=x(15-x)
=-x2 +15x,(0<x<15).
(2) 用细铁丝围一个面积为 1 cm2 的矩形,试将所用铁丝
的长度 l (单位:cm) 表示为矩形的某条边长 x (单位:
cm) 的函数.
解 设矩形的某一条边长为x(cm),
则 x>0,另一条边长为(cm),
所以铁丝的长度 l=2x+,x>0.
4. 下列图象中,表示函数关系 y=f(x) 的有________.
(1)(4)
习题 5.2
感受·理解
1. 物体从静止开始下落,下落的距离与下落时间的平方
成正比. 已知开始下落的 2s 内,物体下落了 19.6,求
开始下落的 3s 内物体下落的距离.
解 由题意设下落的距离y与时间t满足 y=kt2(k≠0),
由已知可得当 t=2 时,y=19.6,
故19.6=4k,解得 k=4.9,
所以 y= 4.9t2
所以当t=3时,y=4.9×32= 44.1.
所以开始下落的3s内物体下落的距离是44.1m.
2. 某公司将进一批单价为 8 元的商品,若按 10 元/个销售,每天可卖出100个;假设销售价每上涨 1 元/个,每天的销售量就减少 10 个.
(1) 设商品的销售价上涨 x 元/个(0≤x≤10,x∈N),每天的利润为 y 元,试用列表法表示函数 y=f(x);
(2) 求销售价为 13 元/个时每天的销售利润;
(3) 如果销售利润为 360 元,那么销售价上涨了多少元
(1) 设商品的销售价上涨 x 元/个(0≤x≤10,x∈N),每
天的利润为 y 元,试用列表法表示函数 y=f(x);
解 y=(10+x-8)(100-10x)
=-10x2+80x+200;
即 y=-10x2+80x+200;
(2) 求销售价为 13 元/个时每天的销售利润;
解 销售价为13元/个时,上涨价3,则每天的销售利润为:
-10×32+80×3+200=350(元);
(3) 如果销售利润为 360 元,那么销售价上涨了多少元
解 销售利润为360元,即 y= 360,
则: -10x2+80x+200=360;
解得 x=4;
即销售价上涨了4元.
3. 设距地面高度 x (单位:km)的气温为 y (单位:℃),在距地面高度不超过11 km时,y 随着 x 的增加而降低,且每升高 1 km,大气温度降低 6 ℃;高度超过 11km 时,气温可视为不变. 设地面气温为22℃,试写出 y=f(x) 的解析式,并分别求高度为 3.5 km 和 12 km 的气温.
y=
22-6x,0 ≤x≤11,
-44,x>11.
f(3.5)= 22-6×3.5=1,
f(12) = - 44.
即高度为 3.5 km 时的气温为1℃,
高度为12 km 时的气温为- 44℃.
4. 建造一个容积为 8 m深为 2 m 的长方体形状的无盖水池,已知池底和池壁的造价分别为 120 元/m2 和 80 元/m2,求总造价 y (单位:元) 关于底面一边长 x (单位:m) 的函数解析式,并指出该函数的定义域.
解 底面一边长为,则另一边长为.
池底的造价为固定值 120×4=480(元),
池壁的造价为变化值
80 ×(2x +2· ) ×2 =320x + ,
则 y= 480+320x+,
定义域为 x∈(0,+∞)
5. 画出函数 f(x) =-x2+x+1(-1≤x≤1) 的图象,并根据图象回答下列问题:
(1)当-1≤x1<x2≤时,比较f(x1)与 f(x2)的大小;
(2) 是否存在 x0∈[-1,1],使得 f(x0)=-2
作出函数 f(x)=-x2+x+1(-1≤x≤1)的图象如下图:
图象为开口向下,且对称轴为x=的抛物线的一段.
(1)当-1≤x1<x2≤时,比较f(x1)与 f(x2)的大小;
解 由图象可知:函数 f(x) 在[-1,]
上是增函数,
∴ -1≤x1<x2≤,
有f(x1) < f(x2);
(2) 是否存在 x0∈[-1,1],使得 f(x0)=-2
解 由图象可知:
当x∈[-1,1] 时,
fmin (x) =f(-1) = -1,
fmax (x) =f() = ,即f(x)∈[-1, ],
∴ 不存在 x0∈[-1,1],使得 f(x0)=-2.
6. 已知A ={1,2,3,4},B = {1,3,5},试写出从
A到B的两个函数.
解 f(x)=x0;g(x)=
1,x=1,2,
3,x=3,4.
(答案不唯一)
7. 已知函数 f(x)= 求 f(2),f(f(-2))的值.
x, x≥0,
x2,x<0,
解 f(2)=2,
f(f(-2))=f(4)=4.
8. 画出函数 y=x3(x∈{-2,-1.5,-1,-0.5,0,0.5,
1,1.5,2})的图象.
思考·运用
9. 某人去上班,先跑步,后步行. 如果 y 表示该人离单位的距离,x 表示出发后的时间,那么下列图象中符合此人走法的是 ( ).
D
10. 请写出 3 个不同的函数 y=f(x) 的解析式满 f(1)=1,
f(2)=4.
解:f(x)=x2;
f(x)=3x-2;
f(x)=2x2-3x+2.(答案不唯一)
11.已知某皮鞋厂一天的生产成本 C (单位:元)与生产数量 n (单位:双)之间的函数关系式是 C=4000 + 50n.
(1)求一天生产1000 双皮鞋的成本;
(2) 如果某天的生产成本是 48 000 元,那么这一天生产了多少双皮鞋
(3) 若每双皮鞋的售价为 90 元,且生产的皮鞋全部售出,试写出这一天的利润 P 关于这一天生产数量 n 的函数关系式,并求出每天至少生产多少双皮鞋,才能不亏本.
(1) 求一天生产1000 双皮鞋的成本;
解 ∵生产成本C(元) 与生产数量n (双) 之间的函数关系是C=4000+50n.
∴n=1000时,C=4000+ 50000=54000;
(2) 如果某天的生产成本是 48 000 元,那么这一天生产了多少双皮鞋
解 令 C=4000+50n=48000,
解得 n=880;
(3) 若每双皮鞋的售价为 90 元,且生产的皮鞋全部售出,试写出这一天的利润 P 关于这一天生产数量 n 的函数关系式,并求出每天至少生产多少双皮鞋,才能不亏本.
解 由题意得:某皮鞋厂一天的生产成本C(元) 与生产数量n(双)之间的函数关系是C=4000+50n.
∴p(n)=90n-(4000+50n)=40n-4000(n∈N+)
要不亏本,必须p(n) >0,解得 n≥100.
即每天至少生产100双皮鞋,才能不亏本.
12. 从2006 年11月15日起国内投首重100g以内的外信的邮资标准是每封信的质量不超过 20g 付邮资 120 分,超过20g 而不超过 40g 付邮资 240分,超过 40g 而不超过 60g 付邮资 360分,依此类推试画出反映每封不超过 90g 的信函应付邮资 y (单位:分)与信函的质量 x (单位:g)之间的函数关系的图象.
解:由题意,得 y=
120,x∈(0,20],
240,x∈(20,40],
360,x∈(40,60],
480,x∈(60,80],
600,x∈(80,90].
图象如图所示.
y/分
x/g
600
480
360
240
120
20
40
60
80
100
O
探究·拓展
13. (开放题) 已知一个函数的解析式为 y=x2,它的值域为区间[1,4],这样的函数有多少个 试写出其中两个函数.
解 设 y=f(x)=x2,
其图象是开口向上的抛物线,其对称轴方程为x=0,是偶函数,
f(x) 在(0,+∞ ) 上单调递增,在(-∞,0) 上单调递减,
要使 y∈[1,4],
故只需确定函数的定义域即可.
当 y=4时,x=±2,当y=1时,x=±1,
这样的函数有无数个,
比如 y=x2,x∈[1,2] ∪{-1},
比如 y=x2,x∈[1,2] ∪{-2}.
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
