弧长和扇形面积 课后同步练习(含答案)
文档属性
| 名称 | 弧长和扇形面积 课后同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 605.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
弧长和扇形面积 课后同步练习
一、选择题(本大题共6小题,每小题3分,共18分)
1. 若扇形的圆心角为90°,半径为6,则该扇形的弧长为( ).
A. π B.2π C.3π D.6π
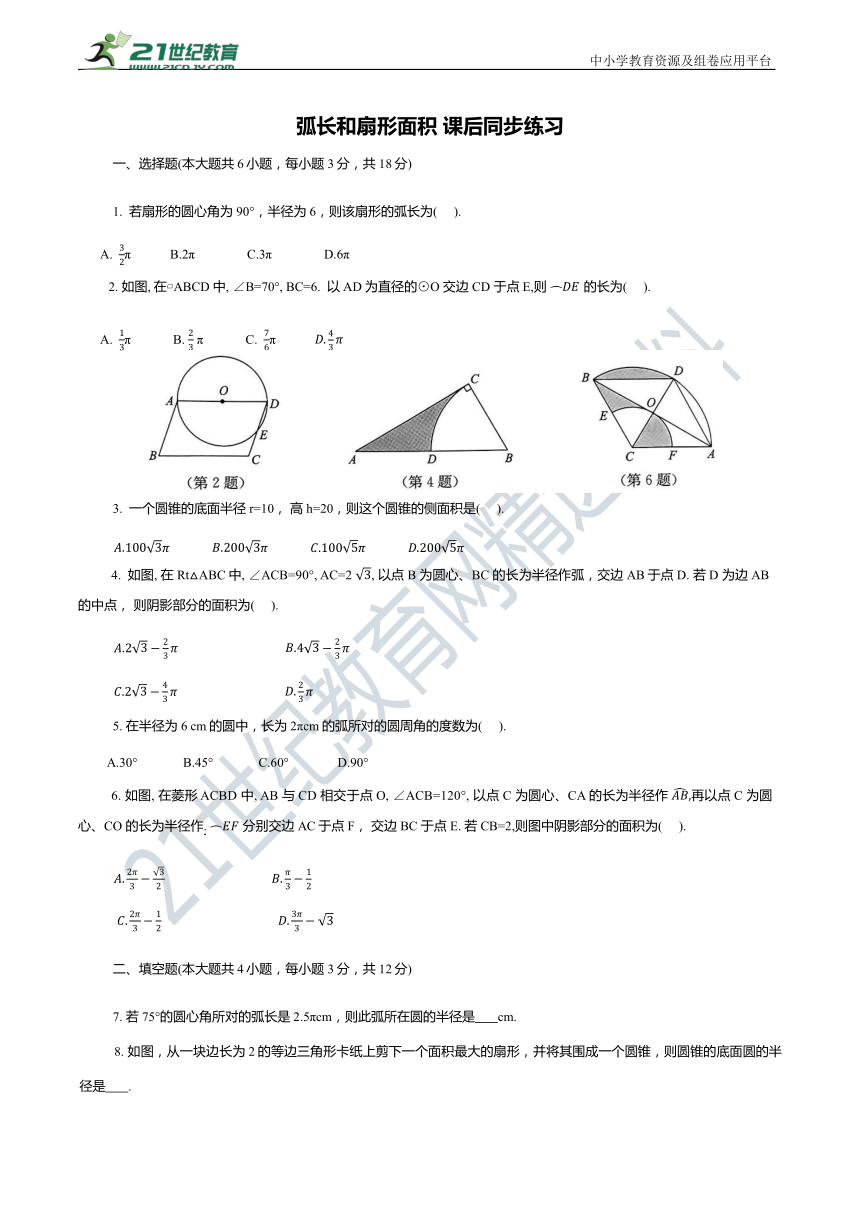
2. 如图, 在 ABCD 中, ∠B=70°, BC=6. 以AD 为直径的⊙O 交边CD 于点E,则 的长为( ).
A. π B. π C. π
3. 一个圆锥的底面半径r=10, 高h=20,则这个圆锥的侧面积是( ).
4. 如图, 在Rt△ABC中, ∠ACB=90°, AC=2 , 以点 B 为圆心、BC 的长为半径作弧,交边AB于点D. 若D 为边AB 的中点, 则阴影部分的面积为( ).
5. 在半径为6 cm的圆中,长为2πcm的弧所对的圆周角的度数为( ).
A.30° B.45° C.60° D.90°
6. 如图, 在菱形 ACBD 中, AB 与CD 相交于点O, ∠ACB=120°, 以点 C 为圆心、CA 的长为半径作 再以点C 为圆心、CO 的长为半径作. 分别交边AC于点 F, 交边BC 于点E. 若CB=2,则图中阴影部分的面积为( ).
二、填空题(本大题共4小题,每小题3分,共12分)
7. 若75°的圆心角所对的弧长是2.5πcm,则此弧所在圆的半径是 cm.
8. 如图,从一块边长为2的等边三角形卡纸上剪下一个面积最大的扇形,并将其围成一个圆锥,则圆锥的底面圆的半径是 .
9. 如图,正方形ABCD 内接于⊙O, 则 的长是 .
10.如图,在扇形OAB中, ∠AOB=90°,半径OB=2,∠BOC=60°, AB,OC 相交于点D,则图中阴影部分的面积为 .
三、解答题(本大题共2小题,每小题10分,共20分. 解答时应写出必要的文字说明、证明过程或演算步骤)
11. 如图,AB 是⊙O 的直径,C,D 是⊙O上的点,OC∥BD 交 AD 于点E, 连接 BC.
(1)求证: AE=ED;
(2)若AB=6,∠ABC=30°, 求图中阴影部分的面积.
12. 如图,BE是⊙O的直径,点A,D在⊙O上, 连接AE,AD,DE, 过点A 作射线AC交BE 的延长线于点C,使∠EAC=∠EDA.
(1)求证: AC 是⊙O 的切线;
(2)若 求阴影部分的面积.
1. C 2. B 3. C 4. A 5. A 6. A
7.6 8. 9. π
11. (1)∵AB 是⊙O的直径,
∴∠ADB=90°.
∵OC∥BD,
∴∠AEO=∠ADB=90°, 即OC⊥AD.
又∵OC为⊙O的半径,
∴AE=ED.
(2)连接CD, OD, 如图.
∵OC=OB,
∴∠OCB=∠ABC=30°,
∴∠AOC=∠OCB+∠ABC=60°.
∵OC⊥AD,
∴∠COD=∠AOC=60°,
∴∠AOD=120°,
∴∠A=∠ADO=30°.
在 Rt△ABD 中, AB=6,
∵OA=OB,AE=ED,
12. (1)如图,连接OA, 过点O作OF⊥AE 于点F.
∵∠AFO=90°,
∴∠EAO+∠AOF=90°.
∵OA=OE,
∴∠EDA=∠AOF.
∵∠EAC=∠EDA,
∴∠EAC=∠AOF,
∴∠EAO+∠EAC=90°.
∵∠EAC+∠EAO=∠CAO,
∴∠CAO=90°, 即OA⊥AC,
∴AC是⊙O的切线.
∵∠EAC+∠C=∠AEO, ∴∠AEO=2∠EAC.
∵OA=OE, ∴∠AEO=∠EAO, ∴∠EAO=2∠EAC.
∵∠EAO+∠EAC=90°,
∴∠EAC=30°, ∠EAO=60°,
∴△OAE 是等边三角形,
在 Rt△OAF 中,
∴阴影部分的面积为
弧长和扇形面积 课后同步练习
一、选择题(本大题共6小题,每小题3分,共18分)
1. 若扇形的圆心角为90°,半径为6,则该扇形的弧长为( ).
A. π B.2π C.3π D.6π
2. 如图, 在 ABCD 中, ∠B=70°, BC=6. 以AD 为直径的⊙O 交边CD 于点E,则 的长为( ).
A. π B. π C. π
3. 一个圆锥的底面半径r=10, 高h=20,则这个圆锥的侧面积是( ).
4. 如图, 在Rt△ABC中, ∠ACB=90°, AC=2 , 以点 B 为圆心、BC 的长为半径作弧,交边AB于点D. 若D 为边AB 的中点, 则阴影部分的面积为( ).
5. 在半径为6 cm的圆中,长为2πcm的弧所对的圆周角的度数为( ).
A.30° B.45° C.60° D.90°
6. 如图, 在菱形 ACBD 中, AB 与CD 相交于点O, ∠ACB=120°, 以点 C 为圆心、CA 的长为半径作 再以点C 为圆心、CO 的长为半径作. 分别交边AC于点 F, 交边BC 于点E. 若CB=2,则图中阴影部分的面积为( ).
二、填空题(本大题共4小题,每小题3分,共12分)
7. 若75°的圆心角所对的弧长是2.5πcm,则此弧所在圆的半径是 cm.
8. 如图,从一块边长为2的等边三角形卡纸上剪下一个面积最大的扇形,并将其围成一个圆锥,则圆锥的底面圆的半径是 .
9. 如图,正方形ABCD 内接于⊙O, 则 的长是 .
10.如图,在扇形OAB中, ∠AOB=90°,半径OB=2,∠BOC=60°, AB,OC 相交于点D,则图中阴影部分的面积为 .
三、解答题(本大题共2小题,每小题10分,共20分. 解答时应写出必要的文字说明、证明过程或演算步骤)
11. 如图,AB 是⊙O 的直径,C,D 是⊙O上的点,OC∥BD 交 AD 于点E, 连接 BC.
(1)求证: AE=ED;
(2)若AB=6,∠ABC=30°, 求图中阴影部分的面积.
12. 如图,BE是⊙O的直径,点A,D在⊙O上, 连接AE,AD,DE, 过点A 作射线AC交BE 的延长线于点C,使∠EAC=∠EDA.
(1)求证: AC 是⊙O 的切线;
(2)若 求阴影部分的面积.
1. C 2. B 3. C 4. A 5. A 6. A
7.6 8. 9. π
11. (1)∵AB 是⊙O的直径,
∴∠ADB=90°.
∵OC∥BD,
∴∠AEO=∠ADB=90°, 即OC⊥AD.
又∵OC为⊙O的半径,
∴AE=ED.
(2)连接CD, OD, 如图.
∵OC=OB,
∴∠OCB=∠ABC=30°,
∴∠AOC=∠OCB+∠ABC=60°.
∵OC⊥AD,
∴∠COD=∠AOC=60°,
∴∠AOD=120°,
∴∠A=∠ADO=30°.
在 Rt△ABD 中, AB=6,
∵OA=OB,AE=ED,
12. (1)如图,连接OA, 过点O作OF⊥AE 于点F.
∵∠AFO=90°,
∴∠EAO+∠AOF=90°.
∵OA=OE,
∴∠EDA=∠AOF.
∵∠EAC=∠EDA,
∴∠EAC=∠AOF,
∴∠EAO+∠EAC=90°.
∵∠EAC+∠EAO=∠CAO,
∴∠CAO=90°, 即OA⊥AC,
∴AC是⊙O的切线.
∵∠EAC+∠C=∠AEO, ∴∠AEO=2∠EAC.
∵OA=OE, ∴∠AEO=∠EAO, ∴∠EAO=2∠EAC.
∵∠EAO+∠EAC=90°,
∴∠EAC=30°, ∠EAO=60°,
∴△OAE 是等边三角形,
在 Rt△OAF 中,
∴阴影部分的面积为
同课章节目录
