5.4 函数的奇偶性 课件(共83张PPT)
文档属性
| 名称 | 5.4 函数的奇偶性 课件(共83张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 66.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 21:38:58 | ||
图片预览











文档简介
(共83张PPT)
第5章
函数概念与性质
5 . 4
函数的奇偶性
在我们的日常生活中,可以观察到许多对称现象:美丽的蝴蝶,盛开的花朵,六角形的雪花晶体,有倒影的山水景色·····
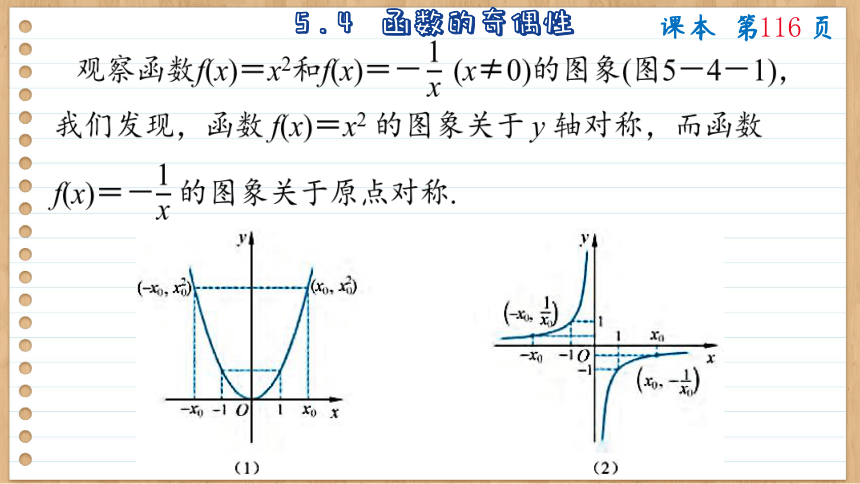
观察函数f(x)=x2和f(x)=- (x≠0)的图象(图5-4-1),我们发现,函数 f(x)=x2 的图象关于 y 轴对称,而函数
f(x)=- 的图象关于原点对称.
● 怎样用数量关系来刻画函数图象的这种对称性
对于函数 f(x)=x2,当自变量取一对相反数时,它们的函数值相等.
例如, f(-2)=4=f(2),
f(-1)=1=f(1),
f(-)==f().
实际上,对于函数f(x)=x2定义域 R 内任意一个x,都有f(-x)=x3=f(x). 这时我们称函数 f(x)=x2为偶函数.
对于函数 f(x)=- (x≠0),当自变量取一对相反数时,它们的函数值也互为相反数.
例如, f(-2)==-f(2),
f(-1)=1= -f(1),
f(-)=3=-f().
实际上,对于函数 f(x)=-定义域{x∣x∈R,x≠0)内任意个x,都有 f(-x)==-f(x).
这时我们称函数 f(x)=- (x≠0)为奇函数.
函数的奇偶性
(1) 奇偶性:
奇偶性 偶函数 奇函数
条件 设函数y=f(x)的定义域为A,如果对于任意的x∈A,都有-x∈A
前提 f(-x) =_______ f(-x) = ________
结论 函数y=f(x)是偶函数 函数y=f(x)是奇函数
图象特点 关于______对称 关于_______对称
f(x)
-f(x)
y轴
原点
(2) 本质:奇偶性是函数对称性的表示方法.
(3) 应用:
奇偶性是函数的“整体”性质,只有对其定义域内的每一个x,都有 f(-x) =-f(x)(或f(-x)=f(x)),才能说 f(x)是奇(偶)函数.
【思考】
具有奇偶性的函数,其定义域有何特点
提示:定义域关于原点对称.
例 1
判定下列函数是否为偶函数或奇函数:
(1) f(x)=x2-1;
解:函数 f(x)=x2-1的定义域是 R .
因为对于任意的x∈R,都有-x∈R,
且 f(-x)=(-x)2-1= x2-1=f(x),
所以函数 f(x)=-1是偶函数.
(2) f(x)=2x;
解:函数 f(x)=2x 的定义域是 R .
因为对于任意的 x∈R,都有-x∈R,
且 f(-x)= 2(-x) =-2x=-f(x),
所以函数 f(x)=2x 是奇函数.
(3) f(x) =2∣x∣;
解:函数 f(x)=2∣x∣的定义域是 R .
因为对于任意的 x∈R,都有-x∈R,
且 f(-x)= 2∣-x∣=2∣x∣=f(x),
所以函数 f(x)=2∣x∣ 是偶函数.
(4) f(x)=(x-1)2.
解:函数 f(x)=(x-1)2 的定义域是 R .
因为f(1) = 0,f(-1)=4, ,
所以 f(1)≠f(-1),f(1)≠-f(-1).
因此,根据函数奇偶性定义可以知道,函数 f(x)=(x-1)2 既不是奇函数,也不是偶函数.
例 2
判断函数 f(x)=x3+5 是否具有奇偶性.
解 函数 f(x)的定义域为 R.
因为对于任意的 x∈R,都有-x∈R,
且f(-x) =(-x)3+5(-x)
=- (x3+5x)=- f(x),
所以函数 y=f(x) 为奇函数.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 对于函数 y=f(x),若存在x,使f(-x)=-f(x),则函数y=f(x)一定是奇函数. ( )
(2) 若函数的定义域关于原点对称,则这个函数不是奇函数就是偶函数. ( )
(3) 奇函数的图象一定过 (0,0). ( )
2. 下列图象表示的函数具有奇偶性的是 ( )
B
解析:B选项的图象关于y轴对称,是偶函数,其余选项都不具有奇偶性.
解析
3. 下列函数为奇函数的是 ( )
A. y=∣x∣ B. y=3-x
C. y= D. y=-x2+14
C
解析:A、D两项,函数均为偶函数,B项中函数为非奇非偶函数,而C项中函数为奇函数.
解析
【跟踪训练】
1.设f(x)是定义在R上的奇函数,且当x≤0时,f(x)=x2-x,
则 f(1) =( ).
A. - B. - C. D.
A
解析:因为f(x)是定义在R上的奇函数,
所以 f(1)=-f(-1)=- .
解析
2.设f(x)是定义在R上的一个函数,则函数F(x)=f(x)-f(-x)
在R上一定 ( )
A. 是奇函数
B. 是偶函数
C. 既是奇函数又是偶函数
D. 既不是奇函数又不是偶函数
A
解析:F(-x) =f(-x) -f(x)
=- [f(x)-f(-x)]
=-F(x),
符合奇函数的定义.
解析
解析:由题图知 f(1)=,f(2)=,
又f(x)为奇函数,
所以f(-2)+f(-1)=-f(2)-f(1)= --=-2.
3. 如图,给出奇函数 y=f(x) 的局部图象,则 f(-2)+f(-1)的值为 ( )
A.1 B.0
C. -2 D.2
C
解析
4. 已知f(x)是定义在R上的偶函数,且在区间(-∞,0)上
是增函数. 若f(-3)=0,则 <0的解集为
_______________________.
{x∣-3<x<0或x>3}
解析:因为f(x)是定义在R上的偶函数,且在区间(-∞,0) 上是增函数,所以f(x)在区间(0,+∞)上是减函数,
所以f(3) =f(-3) =0.
当x>0时,f(x)<0,解得x>3;
当x<0时,f(x)>0,解得-3<x<0.
解析
5. 已知函数 f(x)=是定义在(-1,1)上的奇函数,
则常数 m,n 的值分别为____________.
0,0
解析:由题意知 f(0)=0,故得 m=0. 由 f(x) 是奇函数知
f(-x) =-f(x),即=
所以 x2-nx+1=x2+nx+1,所以n=0.
解析
探 究
具有奇偶性的函数,其定义域具有怎样的特点
练 习
1. 函数 f(x)= ( ).
A. 是奇函数但不是偶函数
B. 是偶函数但不是奇函数
C. 既是奇函数又是偶函数
D. 既不是奇函数也不是偶函数
B
2. 函数 f(x) = x2+2x 的图象是否关于某条直线对称
它是否为偶函数
解 f(x)=x2+2x=(x+1)2-1,
由二次函数的性质可知,函数 f(x)=x2+2x 的图象关于直线 x=-1 对称,
∵偶函数的图象关于 y 轴对称
∴函数 f(x)=x2+2x 不是偶函数.
3. 已知函数 f(x) 在 y 轴右边的图象如图所示.
(1)若f(x)是偶函数,试画出函数f(x)在y轴左边的图象;
(2)若 f(x)是奇函数,试画出函数 f(x) 在 y 轴左边的图象.
4. 对于定义在 R 上的函数 f(x),下列判断是否正确
(1) 若 f(x) 是偶函数,则 f(-2)=f(2);
解 若 f(x) 是偶函数,则对任意实数x都有 f(-x)=f(x),
所以,f(-2)=f(2)成立,该判断正确;
(2) 若 f(-2)=f(2),则函数 f(x) 是偶函数;
解 若 f(-2)=f(2),
但是不一定有对任意实数x都有f(-x)=f(x)成立,
不满足偶函数的定义,该判断错误;
(3) 若 f(-2)≠f(2),则函数 f(x)不是偶函数;
解 若 f(-2)≠f(2),
则对任意实数 x 都有 f(-x)=f(x) 不成立,
根据偶函数的定义可知,f(x)不是偶函数该判断正确;
(4) 若 f(-2)=f(2),则函数 f(x)不是奇函数.
解 若取 f(x)=x3-4x,
满足 f(-2)=f(2),
但 f(x)是奇函数,该判断错误.
5. 证明函数 f(x)=x3-x 在 R 上是奇函数.
证明:∵f(x)=x3-x,定义域为R,
∴f(-x)=(-x)3- (-x)
=-x3+x
=-(x3-x)=-f(x),
∴函数 f(x)=x3-x在R上是奇函数.
6. 判断下列函数的奇偶性:
(1) f(x)=x+;
解 ∵f(x)=x+的定义域为:(-∞,0) ∪(0,+∞),
定义域关于原点对称,
又∵f(-x) =-x+=-(x+) = -f(x),
∴ f(x)=x+为奇函数.
(2) f(x)=;
解 ∵f(x)=的定义域为:(-∞,0)∪(0,+∞),
定义域关于原点对称,
又∵f(-x)= == f(x),
∴ f(x)= 为偶函数.
(3) f(x)= 2∣x∣-3.
解 ∵ f(x)=2∣x∣-3 的定义域为R,
其定义域关于原点对称,
又∵ f(-x)=2∣-x∣-3=2∣x∣-3=f(x),
∴ f(x)=2∣x∣-3 为偶函数.
7. 求证:
(1) f(x)=∣x+3∣+∣x-3∣是 R 上的偶函数;
解 ∵ f(x)=∣x+3∣+∣x-3∣的定义域为R,
∴ f(-x) =∣-x+3∣+∣-x-3∣
=∣x-3∣+∣x+3∣=f(x),
∴函数 f(x) 为偶函数;
(2) g(x)=∣x+3∣-∣x-3∣是 R 上的奇函数;
解 ∵g(x)=∣x+3∣-∣x-3∣的定义域为R,
∴g(-x) =∣-x+3∣-∣-x-3∣
=∣x-3∣-∣x+3∣=-g(x).
∴ 函数g(x)为奇函数.
习题 5.4
感受·理解
1. 下列函数哪些是奇函数 哪些是偶函数 哪些既不是奇
函数也不是偶函数
(1) f(x)=2x2-7;
(2) f(x)=x3+5x;
(3) f(x)=5x-3.
(1) f(x)=2x2-7;
解 f(x)=2x2-7的定义域为(-∞,+∞),
定义域关于原点对称,
∵f(-x)=2(-x)2-7=2x-7=f(x),
∴函数 f(x)=2x2-7 是偶函数.
(2) f(x)=x3+5x;
解 f(x)=x3+5x 的定义域为(-∞,+∞),
定义域关于原点对称,
∵f(-x)=(-x)5+5(-x) =-x3-5x=-f(x),
∴函数 f(x)=x3+5x 是奇函数.
(3) f(x)=5x-3.
解 f(x)=5x-3 的定义域为(-∞,+∞),
f(-x)=5·(-x)-3=-5x-3,
-f(x) =-5x+3,
∴f(-x)≠f(x),f(-x)≠-f(x),
∴f(x)=5x-3既不是奇函数也不是偶函数.
2. 已知函数 f(x)=x2-2∣x∣-1,试判断函数 f(x) 的奇
偶性,并画出函数的图象.
解 函数 f(x)= x2-2∣x∣-1的定义域为R,
关于原点对称,
∵ f(-x)=(-x)2-2∣x∣-1=x2-2∣x∣-1=f(x),
∴函数 f(x)=x2-2∣x∣-1 是偶函数函数.
函数 f(x)= x2-2∣x∣-1 =
=
x2-2x-1,x≥0,
x2+2x-1,x<0,
(x-1)2-2,x≥0,
(x+1)2-2 ,x<0,
先作出函数 y=(x-1)2-2,x≥0 的图象,
然后作它关于y轴的对称图象,合起来即得f(x)的图象,
如图所示:
3. 证明函数 f(x) = x3+ 的图象关于原点对称.
解 函数 f(x)=x3+ 的定义域是(-∞,0)∪(0,+∞),
关于原点对称,
∵f(-x)=(-x)3+=-x3-=-f(x).
∴函数 f(x)=x3+是奇函数,
∴函数 f(x)=x3+的图象关于原点对称.
4. 证明函数 g(x)=∣x∣+x2 的图象关于 y 轴对称.
解 由题意,g(x)=∣x∣+x2 的定义域为R,
关于原点对称,
且g(-x)=∣-x∣+(-x)2=∣x∣+(x)2=g(x),
∴g(x)=∣x∣+x2为偶函数,图象关于y轴对称.
思考·运用
5. 设 m 为实数,函数f(x)=x2+mx+1是函数,求m的值.
解 ∵函数f(x)的定义域是R关于原点对称,
又∵f(x)是偶函数,
∴f(-x)=(-x)2-mx+1=x2+mx+1=f(x)恒成立,
∴2mx=0 恒成立,
∵x∈R,
∴m=0.
6. 已知函数 f(x)=ax3-bx+1,a,b∈R,且f(-2)=-1,
求 f(2) 的值.
解 ∵ f(x)=ax3-bx+1,
∴ f(-2)=a(-2)3-b(-2)+1
=-8a+2b+1=-1,
解得:8a-2b=2.
∴f(2)=a·23-2b+1 = 8a-2b+1=2+1=3.
7. 已知函数 y = f(x) 是 R 上的奇函数,且当 x>0 时,
f(x) = 1,求函数 y = f(x) 的表达式.
解 设 x<0,则-x>0,f(-x)=1.
而函数 y=f(x) 是R上奇函数
则 f(-x)=-f(x)=1即 f(x)=-1
∴当x<0时,f(x)=-1.
根据函数 y=f(x) 是 R 上奇函数则f(-0)=-f(0)=f(0)
即 f(0)=0,
综上所述函数 y=f(x) 的表达式是
f(x) =
1,(x>0),
0,(x=0),
-1,(x<0).
8. 已知函数 f(x) 的定义域为R.
(1) 求证:函数 g(x)=f(x)+f(-x)为R上的偶函数;
解 ∵函数 f(x) 的定域为R,
∴函数 g(x)=f(x)+f(-x) 的定义域为R,
即函数 g(x) 的定义域关于原点对称,
又∵g(-x)=f(-x)+f[-(-x)]=f(-x) +f(x)=g(x),
∴函数 g(x)=f(x)+f(-x)是在R上的偶数;
(2) 求证:函数 h(x)=f(x)-f(-x)为 R 上的函数;
解 ∵数 f(x) 的定域为R,
∴函数 h(x)=f(x)-f(-x)的定义域为R,
即函数 h(x) 的定义域关于原点对称,
又∵h(-x)=f(-x) -f[-(-x)]
=f(-x)-f(x)=-h(x),
∴ 函数h(x)=f(-x)-f(x)是在R上的奇数;
(3) 试判断:定义在 R 上的函数 f(x) 能否表示为一个函数
和一个偶函数的和.
解 ∵函数 f(x) 的定义域为R,
令G(x)=, H(x)= ,
则G(x)+H(x)= + = f(x),
由(1)知 G(x)= 是偶函数,
由(2)知 H(x)= 是奇函数,
且 f(x)=G(x)+H(x),
即定义在R上的函数f(x)能表示为一个奇函数和一个偶函数的和.
探究·拓展
9. 设a为给定实数,函数 f(x) 的定义域为 A.
(1) 若对于任意 x∈A,都有 f(a-x)-f(a+x)=0,问:
此函数的图象一定具有怎样的对称性 说明理由.
解 对于任意的 x∈A,都有 f(a-x) -f(a+x)=0,
则函数 y=f(x)图象关于直线 x=a对称.
理由如下:
设函数 y=f(x)图象上任意一点P(x0,y0),则y0=f(x0),
且P关于直线 x=a 的对称点为P′(2a-x0,y0),
由f(a-x)=f(a+x),用x-a取代上式中的x,
得f(2a-x)=f(x)则,f(2a-x0)=f(x0)=y0,
故P′(2a-x0,y0) 在函数 y=f(x) 的图象上,
所以函数 y=f(x) 的图象关于直线 x=a 对称.
(2) 若对于任意 x∈A,都有 f(a-x)+f(a+x)=0,问:
此数的图象一定具有怎样的对称性 说明理由.
解 对于任意的 x∈A, 都有f(a-x)+f(a+x)=0,
则函数 y=f(x)图象关于点 (a,0) 对称.
理由如下:
设函数 y=f(x) 图象上任意一点 P1(x1,y1),则y1=f(x1).
且P1关于点 (a,0) 的对称点为P1′(2a-x1,-y1),
由f(a-x)+f(a+x)=0,用x-a取代上式中的x,
得f(2a-x)=-f(x),则f(2a-x1)=-f(x1)=-y1,
故P′(2a-x1,-1) 在函数 y=f(x) 图象上,
∴函数 y=f(x) 图象关于点(a,0)对称.
链 接
映射的概念
我们已经知道,函数是建立在两个非空数集之间的一种对应关系:对于集合 A中的每一个实数 x ,在集合 B中都有唯一的实数 y 和它对应. 是否存在两个普通集合之间的类似的对应关系呢
例如,坐标平面内的所有点组成的集合为 A,所有的有序数对组成的集合为
B= {(x,y)∣x∈R,y∈R}.
让每一点与其坐标对应,则 A 中的每一个元素(点),在 B 中都有唯一的元素(有序数对)与之对应.
一般地,设 A,B 是两个非空集合,如果按某种对应关系 f,对于A 中的每一个元素,在 B中都有唯一的元素与之对应,那么这样的对应称为从集合 A 到集合 B 的映射(mapping),记为
f:A→B
例
如图所示的对应中:
根据映射的定义,可以知道图中,(4)的对应是从 A到B 的映射(1)(2)(3)的对应不是从 A到B 的映射.
请思考:
1. 假定某高中每个班级都有 45 位同学,每个班级学生按 1~45进行编号,全校学生的姓名都不相同. 设集合 A={x∣x为某高中的学生的姓名),B={x∣1≤x≤45,x∈N},f:每个学生姓名对应学生的编号;g: 每个编号对应学生的姓名. 问:f是否为从A到B的映射 g是否为从B到A的映射
2. 设A=B={a,b,c,d,e,···,x,y,z}(元素为 26
个英文字母),作映射 f:A→B为
并称 A 中字母拼成的文字为明文,相应的 B中对应字母拼成的文字为密文.
(1) mathematics 的密文是什么
(2) 试破译密文 ju jt gvooz.
3. 如图,小明同学在学习
映射时,找到了生活中的一
个实例—纽扣对应,你能再
举一些生活中与映射有关的
例子吗
4.映射与函数有什么区别与联系
问题与探究
f(x)+g(x),f(x)g(x) 和 f(g(x))的单调性
我们知道,函数 f(x)=x2与 g(x)=2x 在R上都是增函数,那么,函数 f(x)+g(x)即 x3+2x 在R上是否仍是增函数 能说明理由吗
一般地,设函数 f(x),g(x)的定义域均为 A,尝试探究:
(1) 若函数 f(x),g(x) 都是增函数,试判别函数 f(x)+g(x) 在定义域 A 上的单调性,并说明理由.又若 f(x),g(x) 都是减函数,结果如何呢 试说明理由.
(2) 函数 f(x),g(x) 都是增函数或都是减函数,判别函数 f(x)g(x) 在定义域 A 上的单调性.
总结上述探究(1)(2),你能得到哪些结论 并继续探究,将你探究的结果填入下表中(用“增函数”“减函数” “不能确定”填空):
f(x) g(x) f(x)+g(x) f(x)+g(x)
增函数 增函数 增函数 不能确定
增函数 减函数 不能确定 不能确定
减函数 增函数 不能确定 不能确定
减函数 减函数 减函数 不能确定
我们知道,定义在 R 上的函数 f(x)=2x 与定义在非负实数集上的函数 g(x)=x2 都是增函数,那么函数 f(g(x))是否仍为增函数 说明理由.
一般地,设函数 f(x) 的定义域为 F,g(x)的定义域为 G,且g(x)的值域为 F 的子集.
(1) 若 f(x),g(x) 都是增函数,试判别 f(g(x))的单调性;
(2)若 f(x)是增函数,g(x)是减函数,试判别f(g(x))的单调性.
总结上述探究(1)(2),你能得到哪些结论 并继续探究,将你探究的结果填入下表中(用“增函数”“减函数” “不能确定”填空):
f(x) g(x) f(g(x))
增函数 增函数 增函数
增函数 减函数 减函数
减函数 增函数 减函数
减函数 减函数 增函数
阅 读
函数概念的形成与发展
1637 年,法国数学家笛卡儿(R.Descartes,1596-1650)在《几何学》中第一次提到“未知和未定的量”,涉及了变量,同时也引入函数的思想.1692年,德国数学家莱布尼茨(G.Leibniz,1646-1716)最早使用“函数”这个词,他用“函数”表示随着曲线的变化而改变的几何量,如切线和点的纵坐标等.
1718 年,瑞士数学家约翰·伯努利( J . Bernoulli,1667
—1748)给出函数新的解释:“由变量 x 和常量用任何方式构成的量都可以叫作 x 的函数,”
1755 年,瑞士数学家欧拉(L.Euler,1707—1783)给出了函数的如下定义:“如果某些变量,以这样一种方式依赖于另一些变量,即当后面这些变量变化时,前面这些变量也随之而改变,那么将前面的变量称为后面变量的函数.”
在函数概念形成的早期阶段,由于接触到的函数都是解析式形式,于是多数人认为函数一定能用解析式表示,他们很难理解不能用解析式表示的函数.
随着微积分等数学领域研究的深入,人们对函数的本质理解也不断加深. 1837 年,德国数学家狄利克雷( P . G . Dirichlet,1805—1859) 认为:“如果对于 x 的每一个值,y 总有一个完全确定的值与之对应,
那么y是工的函数.”此外,他还给出了“狄利克雷函数”:
1, x 为有理数,
y=D(x) =
0, x 为无理数.
自此,人们对函数的本质有了深刻的理解.“变量y是x的函数”意味着:只要有一个法则存在,使得这个函数定义域中的每一个值x,有一个确定的y值和它对应,而不管这个法则是公式、图象、表格还是其他形式.
19 世纪 70 年代后,集合概念的出现使函数概念又得到进一步的发展. 人们用集合和对应的语言来定义函数概念,可以更深入地理解函数本质.
1859 年,我国清朝数学家李善兰 (1811-1882) 将 function 一词译成“函数”,并给出定义:“凡此变数中函彼变数,则此为彼之函数.”这里的“函”,是包含的意思.在国外的数学书上,习惯将函数(即对应关系)记为 f,而在国内的数学书上,通常将函数写为 f(x).
写 作
收集函数概念的形成与发展的历史资料,撰写小论文,论述函数发展的过程、重要的结果,函数发展中的重要人物、事件及其对人类文明的贡献.
本课结束
This lesson is over
THANKS!
第5章
函数概念与性质
5 . 4
函数的奇偶性
在我们的日常生活中,可以观察到许多对称现象:美丽的蝴蝶,盛开的花朵,六角形的雪花晶体,有倒影的山水景色·····
观察函数f(x)=x2和f(x)=- (x≠0)的图象(图5-4-1),我们发现,函数 f(x)=x2 的图象关于 y 轴对称,而函数
f(x)=- 的图象关于原点对称.
● 怎样用数量关系来刻画函数图象的这种对称性
对于函数 f(x)=x2,当自变量取一对相反数时,它们的函数值相等.
例如, f(-2)=4=f(2),
f(-1)=1=f(1),
f(-)==f().
实际上,对于函数f(x)=x2定义域 R 内任意一个x,都有f(-x)=x3=f(x). 这时我们称函数 f(x)=x2为偶函数.
对于函数 f(x)=- (x≠0),当自变量取一对相反数时,它们的函数值也互为相反数.
例如, f(-2)==-f(2),
f(-1)=1= -f(1),
f(-)=3=-f().
实际上,对于函数 f(x)=-定义域{x∣x∈R,x≠0)内任意个x,都有 f(-x)==-f(x).
这时我们称函数 f(x)=- (x≠0)为奇函数.
函数的奇偶性
(1) 奇偶性:
奇偶性 偶函数 奇函数
条件 设函数y=f(x)的定义域为A,如果对于任意的x∈A,都有-x∈A
前提 f(-x) =_______ f(-x) = ________
结论 函数y=f(x)是偶函数 函数y=f(x)是奇函数
图象特点 关于______对称 关于_______对称
f(x)
-f(x)
y轴
原点
(2) 本质:奇偶性是函数对称性的表示方法.
(3) 应用:
奇偶性是函数的“整体”性质,只有对其定义域内的每一个x,都有 f(-x) =-f(x)(或f(-x)=f(x)),才能说 f(x)是奇(偶)函数.
【思考】
具有奇偶性的函数,其定义域有何特点
提示:定义域关于原点对称.
例 1
判定下列函数是否为偶函数或奇函数:
(1) f(x)=x2-1;
解:函数 f(x)=x2-1的定义域是 R .
因为对于任意的x∈R,都有-x∈R,
且 f(-x)=(-x)2-1= x2-1=f(x),
所以函数 f(x)=-1是偶函数.
(2) f(x)=2x;
解:函数 f(x)=2x 的定义域是 R .
因为对于任意的 x∈R,都有-x∈R,
且 f(-x)= 2(-x) =-2x=-f(x),
所以函数 f(x)=2x 是奇函数.
(3) f(x) =2∣x∣;
解:函数 f(x)=2∣x∣的定义域是 R .
因为对于任意的 x∈R,都有-x∈R,
且 f(-x)= 2∣-x∣=2∣x∣=f(x),
所以函数 f(x)=2∣x∣ 是偶函数.
(4) f(x)=(x-1)2.
解:函数 f(x)=(x-1)2 的定义域是 R .
因为f(1) = 0,f(-1)=4, ,
所以 f(1)≠f(-1),f(1)≠-f(-1).
因此,根据函数奇偶性定义可以知道,函数 f(x)=(x-1)2 既不是奇函数,也不是偶函数.
例 2
判断函数 f(x)=x3+5 是否具有奇偶性.
解 函数 f(x)的定义域为 R.
因为对于任意的 x∈R,都有-x∈R,
且f(-x) =(-x)3+5(-x)
=- (x3+5x)=- f(x),
所以函数 y=f(x) 为奇函数.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 对于函数 y=f(x),若存在x,使f(-x)=-f(x),则函数y=f(x)一定是奇函数. ( )
(2) 若函数的定义域关于原点对称,则这个函数不是奇函数就是偶函数. ( )
(3) 奇函数的图象一定过 (0,0). ( )
2. 下列图象表示的函数具有奇偶性的是 ( )
B
解析:B选项的图象关于y轴对称,是偶函数,其余选项都不具有奇偶性.
解析
3. 下列函数为奇函数的是 ( )
A. y=∣x∣ B. y=3-x
C. y= D. y=-x2+14
C
解析:A、D两项,函数均为偶函数,B项中函数为非奇非偶函数,而C项中函数为奇函数.
解析
【跟踪训练】
1.设f(x)是定义在R上的奇函数,且当x≤0时,f(x)=x2-x,
则 f(1) =( ).
A. - B. - C. D.
A
解析:因为f(x)是定义在R上的奇函数,
所以 f(1)=-f(-1)=- .
解析
2.设f(x)是定义在R上的一个函数,则函数F(x)=f(x)-f(-x)
在R上一定 ( )
A. 是奇函数
B. 是偶函数
C. 既是奇函数又是偶函数
D. 既不是奇函数又不是偶函数
A
解析:F(-x) =f(-x) -f(x)
=- [f(x)-f(-x)]
=-F(x),
符合奇函数的定义.
解析
解析:由题图知 f(1)=,f(2)=,
又f(x)为奇函数,
所以f(-2)+f(-1)=-f(2)-f(1)= --=-2.
3. 如图,给出奇函数 y=f(x) 的局部图象,则 f(-2)+f(-1)的值为 ( )
A.1 B.0
C. -2 D.2
C
解析
4. 已知f(x)是定义在R上的偶函数,且在区间(-∞,0)上
是增函数. 若f(-3)=0,则 <0的解集为
_______________________.
{x∣-3<x<0或x>3}
解析:因为f(x)是定义在R上的偶函数,且在区间(-∞,0) 上是增函数,所以f(x)在区间(0,+∞)上是减函数,
所以f(3) =f(-3) =0.
当x>0时,f(x)<0,解得x>3;
当x<0时,f(x)>0,解得-3<x<0.
解析
5. 已知函数 f(x)=是定义在(-1,1)上的奇函数,
则常数 m,n 的值分别为____________.
0,0
解析:由题意知 f(0)=0,故得 m=0. 由 f(x) 是奇函数知
f(-x) =-f(x),即=
所以 x2-nx+1=x2+nx+1,所以n=0.
解析
探 究
具有奇偶性的函数,其定义域具有怎样的特点
练 习
1. 函数 f(x)= ( ).
A. 是奇函数但不是偶函数
B. 是偶函数但不是奇函数
C. 既是奇函数又是偶函数
D. 既不是奇函数也不是偶函数
B
2. 函数 f(x) = x2+2x 的图象是否关于某条直线对称
它是否为偶函数
解 f(x)=x2+2x=(x+1)2-1,
由二次函数的性质可知,函数 f(x)=x2+2x 的图象关于直线 x=-1 对称,
∵偶函数的图象关于 y 轴对称
∴函数 f(x)=x2+2x 不是偶函数.
3. 已知函数 f(x) 在 y 轴右边的图象如图所示.
(1)若f(x)是偶函数,试画出函数f(x)在y轴左边的图象;
(2)若 f(x)是奇函数,试画出函数 f(x) 在 y 轴左边的图象.
4. 对于定义在 R 上的函数 f(x),下列判断是否正确
(1) 若 f(x) 是偶函数,则 f(-2)=f(2);
解 若 f(x) 是偶函数,则对任意实数x都有 f(-x)=f(x),
所以,f(-2)=f(2)成立,该判断正确;
(2) 若 f(-2)=f(2),则函数 f(x) 是偶函数;
解 若 f(-2)=f(2),
但是不一定有对任意实数x都有f(-x)=f(x)成立,
不满足偶函数的定义,该判断错误;
(3) 若 f(-2)≠f(2),则函数 f(x)不是偶函数;
解 若 f(-2)≠f(2),
则对任意实数 x 都有 f(-x)=f(x) 不成立,
根据偶函数的定义可知,f(x)不是偶函数该判断正确;
(4) 若 f(-2)=f(2),则函数 f(x)不是奇函数.
解 若取 f(x)=x3-4x,
满足 f(-2)=f(2),
但 f(x)是奇函数,该判断错误.
5. 证明函数 f(x)=x3-x 在 R 上是奇函数.
证明:∵f(x)=x3-x,定义域为R,
∴f(-x)=(-x)3- (-x)
=-x3+x
=-(x3-x)=-f(x),
∴函数 f(x)=x3-x在R上是奇函数.
6. 判断下列函数的奇偶性:
(1) f(x)=x+;
解 ∵f(x)=x+的定义域为:(-∞,0) ∪(0,+∞),
定义域关于原点对称,
又∵f(-x) =-x+=-(x+) = -f(x),
∴ f(x)=x+为奇函数.
(2) f(x)=;
解 ∵f(x)=的定义域为:(-∞,0)∪(0,+∞),
定义域关于原点对称,
又∵f(-x)= == f(x),
∴ f(x)= 为偶函数.
(3) f(x)= 2∣x∣-3.
解 ∵ f(x)=2∣x∣-3 的定义域为R,
其定义域关于原点对称,
又∵ f(-x)=2∣-x∣-3=2∣x∣-3=f(x),
∴ f(x)=2∣x∣-3 为偶函数.
7. 求证:
(1) f(x)=∣x+3∣+∣x-3∣是 R 上的偶函数;
解 ∵ f(x)=∣x+3∣+∣x-3∣的定义域为R,
∴ f(-x) =∣-x+3∣+∣-x-3∣
=∣x-3∣+∣x+3∣=f(x),
∴函数 f(x) 为偶函数;
(2) g(x)=∣x+3∣-∣x-3∣是 R 上的奇函数;
解 ∵g(x)=∣x+3∣-∣x-3∣的定义域为R,
∴g(-x) =∣-x+3∣-∣-x-3∣
=∣x-3∣-∣x+3∣=-g(x).
∴ 函数g(x)为奇函数.
习题 5.4
感受·理解
1. 下列函数哪些是奇函数 哪些是偶函数 哪些既不是奇
函数也不是偶函数
(1) f(x)=2x2-7;
(2) f(x)=x3+5x;
(3) f(x)=5x-3.
(1) f(x)=2x2-7;
解 f(x)=2x2-7的定义域为(-∞,+∞),
定义域关于原点对称,
∵f(-x)=2(-x)2-7=2x-7=f(x),
∴函数 f(x)=2x2-7 是偶函数.
(2) f(x)=x3+5x;
解 f(x)=x3+5x 的定义域为(-∞,+∞),
定义域关于原点对称,
∵f(-x)=(-x)5+5(-x) =-x3-5x=-f(x),
∴函数 f(x)=x3+5x 是奇函数.
(3) f(x)=5x-3.
解 f(x)=5x-3 的定义域为(-∞,+∞),
f(-x)=5·(-x)-3=-5x-3,
-f(x) =-5x+3,
∴f(-x)≠f(x),f(-x)≠-f(x),
∴f(x)=5x-3既不是奇函数也不是偶函数.
2. 已知函数 f(x)=x2-2∣x∣-1,试判断函数 f(x) 的奇
偶性,并画出函数的图象.
解 函数 f(x)= x2-2∣x∣-1的定义域为R,
关于原点对称,
∵ f(-x)=(-x)2-2∣x∣-1=x2-2∣x∣-1=f(x),
∴函数 f(x)=x2-2∣x∣-1 是偶函数函数.
函数 f(x)= x2-2∣x∣-1 =
=
x2-2x-1,x≥0,
x2+2x-1,x<0,
(x-1)2-2,x≥0,
(x+1)2-2 ,x<0,
先作出函数 y=(x-1)2-2,x≥0 的图象,
然后作它关于y轴的对称图象,合起来即得f(x)的图象,
如图所示:
3. 证明函数 f(x) = x3+ 的图象关于原点对称.
解 函数 f(x)=x3+ 的定义域是(-∞,0)∪(0,+∞),
关于原点对称,
∵f(-x)=(-x)3+=-x3-=-f(x).
∴函数 f(x)=x3+是奇函数,
∴函数 f(x)=x3+的图象关于原点对称.
4. 证明函数 g(x)=∣x∣+x2 的图象关于 y 轴对称.
解 由题意,g(x)=∣x∣+x2 的定义域为R,
关于原点对称,
且g(-x)=∣-x∣+(-x)2=∣x∣+(x)2=g(x),
∴g(x)=∣x∣+x2为偶函数,图象关于y轴对称.
思考·运用
5. 设 m 为实数,函数f(x)=x2+mx+1是函数,求m的值.
解 ∵函数f(x)的定义域是R关于原点对称,
又∵f(x)是偶函数,
∴f(-x)=(-x)2-mx+1=x2+mx+1=f(x)恒成立,
∴2mx=0 恒成立,
∵x∈R,
∴m=0.
6. 已知函数 f(x)=ax3-bx+1,a,b∈R,且f(-2)=-1,
求 f(2) 的值.
解 ∵ f(x)=ax3-bx+1,
∴ f(-2)=a(-2)3-b(-2)+1
=-8a+2b+1=-1,
解得:8a-2b=2.
∴f(2)=a·23-2b+1 = 8a-2b+1=2+1=3.
7. 已知函数 y = f(x) 是 R 上的奇函数,且当 x>0 时,
f(x) = 1,求函数 y = f(x) 的表达式.
解 设 x<0,则-x>0,f(-x)=1.
而函数 y=f(x) 是R上奇函数
则 f(-x)=-f(x)=1即 f(x)=-1
∴当x<0时,f(x)=-1.
根据函数 y=f(x) 是 R 上奇函数则f(-0)=-f(0)=f(0)
即 f(0)=0,
综上所述函数 y=f(x) 的表达式是
f(x) =
1,(x>0),
0,(x=0),
-1,(x<0).
8. 已知函数 f(x) 的定义域为R.
(1) 求证:函数 g(x)=f(x)+f(-x)为R上的偶函数;
解 ∵函数 f(x) 的定域为R,
∴函数 g(x)=f(x)+f(-x) 的定义域为R,
即函数 g(x) 的定义域关于原点对称,
又∵g(-x)=f(-x)+f[-(-x)]=f(-x) +f(x)=g(x),
∴函数 g(x)=f(x)+f(-x)是在R上的偶数;
(2) 求证:函数 h(x)=f(x)-f(-x)为 R 上的函数;
解 ∵数 f(x) 的定域为R,
∴函数 h(x)=f(x)-f(-x)的定义域为R,
即函数 h(x) 的定义域关于原点对称,
又∵h(-x)=f(-x) -f[-(-x)]
=f(-x)-f(x)=-h(x),
∴ 函数h(x)=f(-x)-f(x)是在R上的奇数;
(3) 试判断:定义在 R 上的函数 f(x) 能否表示为一个函数
和一个偶函数的和.
解 ∵函数 f(x) 的定义域为R,
令G(x)=, H(x)= ,
则G(x)+H(x)= + = f(x),
由(1)知 G(x)= 是偶函数,
由(2)知 H(x)= 是奇函数,
且 f(x)=G(x)+H(x),
即定义在R上的函数f(x)能表示为一个奇函数和一个偶函数的和.
探究·拓展
9. 设a为给定实数,函数 f(x) 的定义域为 A.
(1) 若对于任意 x∈A,都有 f(a-x)-f(a+x)=0,问:
此函数的图象一定具有怎样的对称性 说明理由.
解 对于任意的 x∈A,都有 f(a-x) -f(a+x)=0,
则函数 y=f(x)图象关于直线 x=a对称.
理由如下:
设函数 y=f(x)图象上任意一点P(x0,y0),则y0=f(x0),
且P关于直线 x=a 的对称点为P′(2a-x0,y0),
由f(a-x)=f(a+x),用x-a取代上式中的x,
得f(2a-x)=f(x)则,f(2a-x0)=f(x0)=y0,
故P′(2a-x0,y0) 在函数 y=f(x) 的图象上,
所以函数 y=f(x) 的图象关于直线 x=a 对称.
(2) 若对于任意 x∈A,都有 f(a-x)+f(a+x)=0,问:
此数的图象一定具有怎样的对称性 说明理由.
解 对于任意的 x∈A, 都有f(a-x)+f(a+x)=0,
则函数 y=f(x)图象关于点 (a,0) 对称.
理由如下:
设函数 y=f(x) 图象上任意一点 P1(x1,y1),则y1=f(x1).
且P1关于点 (a,0) 的对称点为P1′(2a-x1,-y1),
由f(a-x)+f(a+x)=0,用x-a取代上式中的x,
得f(2a-x)=-f(x),则f(2a-x1)=-f(x1)=-y1,
故P′(2a-x1,-1) 在函数 y=f(x) 图象上,
∴函数 y=f(x) 图象关于点(a,0)对称.
链 接
映射的概念
我们已经知道,函数是建立在两个非空数集之间的一种对应关系:对于集合 A中的每一个实数 x ,在集合 B中都有唯一的实数 y 和它对应. 是否存在两个普通集合之间的类似的对应关系呢
例如,坐标平面内的所有点组成的集合为 A,所有的有序数对组成的集合为
B= {(x,y)∣x∈R,y∈R}.
让每一点与其坐标对应,则 A 中的每一个元素(点),在 B 中都有唯一的元素(有序数对)与之对应.
一般地,设 A,B 是两个非空集合,如果按某种对应关系 f,对于A 中的每一个元素,在 B中都有唯一的元素与之对应,那么这样的对应称为从集合 A 到集合 B 的映射(mapping),记为
f:A→B
例
如图所示的对应中:
根据映射的定义,可以知道图中,(4)的对应是从 A到B 的映射(1)(2)(3)的对应不是从 A到B 的映射.
请思考:
1. 假定某高中每个班级都有 45 位同学,每个班级学生按 1~45进行编号,全校学生的姓名都不相同. 设集合 A={x∣x为某高中的学生的姓名),B={x∣1≤x≤45,x∈N},f:每个学生姓名对应学生的编号;g: 每个编号对应学生的姓名. 问:f是否为从A到B的映射 g是否为从B到A的映射
2. 设A=B={a,b,c,d,e,···,x,y,z}(元素为 26
个英文字母),作映射 f:A→B为
并称 A 中字母拼成的文字为明文,相应的 B中对应字母拼成的文字为密文.
(1) mathematics 的密文是什么
(2) 试破译密文 ju jt gvooz.
3. 如图,小明同学在学习
映射时,找到了生活中的一
个实例—纽扣对应,你能再
举一些生活中与映射有关的
例子吗
4.映射与函数有什么区别与联系
问题与探究
f(x)+g(x),f(x)g(x) 和 f(g(x))的单调性
我们知道,函数 f(x)=x2与 g(x)=2x 在R上都是增函数,那么,函数 f(x)+g(x)即 x3+2x 在R上是否仍是增函数 能说明理由吗
一般地,设函数 f(x),g(x)的定义域均为 A,尝试探究:
(1) 若函数 f(x),g(x) 都是增函数,试判别函数 f(x)+g(x) 在定义域 A 上的单调性,并说明理由.又若 f(x),g(x) 都是减函数,结果如何呢 试说明理由.
(2) 函数 f(x),g(x) 都是增函数或都是减函数,判别函数 f(x)g(x) 在定义域 A 上的单调性.
总结上述探究(1)(2),你能得到哪些结论 并继续探究,将你探究的结果填入下表中(用“增函数”“减函数” “不能确定”填空):
f(x) g(x) f(x)+g(x) f(x)+g(x)
增函数 增函数 增函数 不能确定
增函数 减函数 不能确定 不能确定
减函数 增函数 不能确定 不能确定
减函数 减函数 减函数 不能确定
我们知道,定义在 R 上的函数 f(x)=2x 与定义在非负实数集上的函数 g(x)=x2 都是增函数,那么函数 f(g(x))是否仍为增函数 说明理由.
一般地,设函数 f(x) 的定义域为 F,g(x)的定义域为 G,且g(x)的值域为 F 的子集.
(1) 若 f(x),g(x) 都是增函数,试判别 f(g(x))的单调性;
(2)若 f(x)是增函数,g(x)是减函数,试判别f(g(x))的单调性.
总结上述探究(1)(2),你能得到哪些结论 并继续探究,将你探究的结果填入下表中(用“增函数”“减函数” “不能确定”填空):
f(x) g(x) f(g(x))
增函数 增函数 增函数
增函数 减函数 减函数
减函数 增函数 减函数
减函数 减函数 增函数
阅 读
函数概念的形成与发展
1637 年,法国数学家笛卡儿(R.Descartes,1596-1650)在《几何学》中第一次提到“未知和未定的量”,涉及了变量,同时也引入函数的思想.1692年,德国数学家莱布尼茨(G.Leibniz,1646-1716)最早使用“函数”这个词,他用“函数”表示随着曲线的变化而改变的几何量,如切线和点的纵坐标等.
1718 年,瑞士数学家约翰·伯努利( J . Bernoulli,1667
—1748)给出函数新的解释:“由变量 x 和常量用任何方式构成的量都可以叫作 x 的函数,”
1755 年,瑞士数学家欧拉(L.Euler,1707—1783)给出了函数的如下定义:“如果某些变量,以这样一种方式依赖于另一些变量,即当后面这些变量变化时,前面这些变量也随之而改变,那么将前面的变量称为后面变量的函数.”
在函数概念形成的早期阶段,由于接触到的函数都是解析式形式,于是多数人认为函数一定能用解析式表示,他们很难理解不能用解析式表示的函数.
随着微积分等数学领域研究的深入,人们对函数的本质理解也不断加深. 1837 年,德国数学家狄利克雷( P . G . Dirichlet,1805—1859) 认为:“如果对于 x 的每一个值,y 总有一个完全确定的值与之对应,
那么y是工的函数.”此外,他还给出了“狄利克雷函数”:
1, x 为有理数,
y=D(x) =
0, x 为无理数.
自此,人们对函数的本质有了深刻的理解.“变量y是x的函数”意味着:只要有一个法则存在,使得这个函数定义域中的每一个值x,有一个确定的y值和它对应,而不管这个法则是公式、图象、表格还是其他形式.
19 世纪 70 年代后,集合概念的出现使函数概念又得到进一步的发展. 人们用集合和对应的语言来定义函数概念,可以更深入地理解函数本质.
1859 年,我国清朝数学家李善兰 (1811-1882) 将 function 一词译成“函数”,并给出定义:“凡此变数中函彼变数,则此为彼之函数.”这里的“函”,是包含的意思.在国外的数学书上,习惯将函数(即对应关系)记为 f,而在国内的数学书上,通常将函数写为 f(x).
写 作
收集函数概念的形成与发展的历史资料,撰写小论文,论述函数发展的过程、重要的结果,函数发展中的重要人物、事件及其对人类文明的贡献.
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
