5.3 函数的单调性 课件(共84张PPT)
文档属性
| 名称 | 5.3 函数的单调性 课件(共84张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 67.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 21:39:33 | ||
图片预览








文档简介
(共84张PPT)
第5章
函数概念与性质
5 . 3
函数的单调性
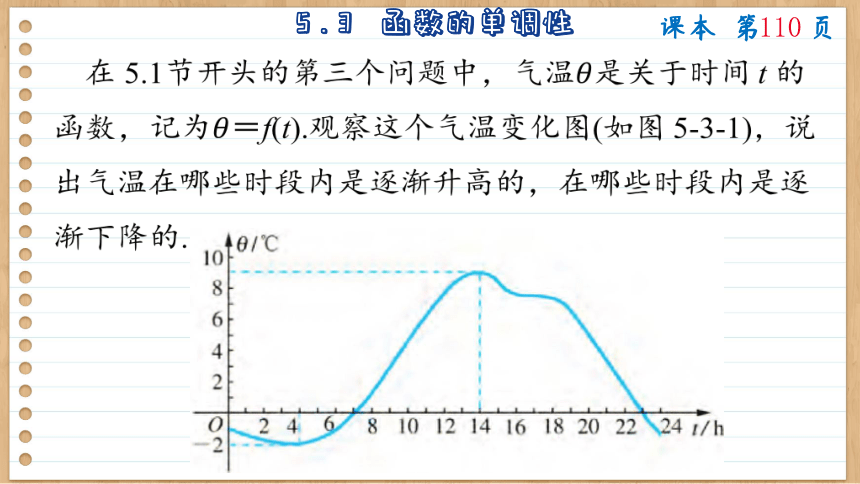
在 5.1节开头的第三个问题中,气温是关于时间 t 的函数,记为=f(t).观察这个气温变化图(如图 5-3-1),说出气温在哪些时段内是逐渐升高的,在哪些时段内是逐渐下降的.
● 怎样用数学语言刻画上述某一时段内“随着时间的增加气温逐渐升高”这一特征
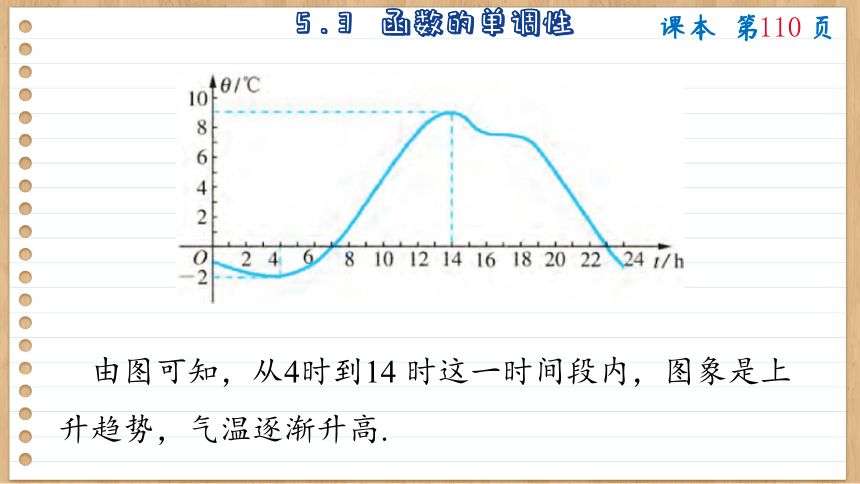
由图可知,从4时到14 时这一时间段内,图象是上升趋势,气温逐渐升高.
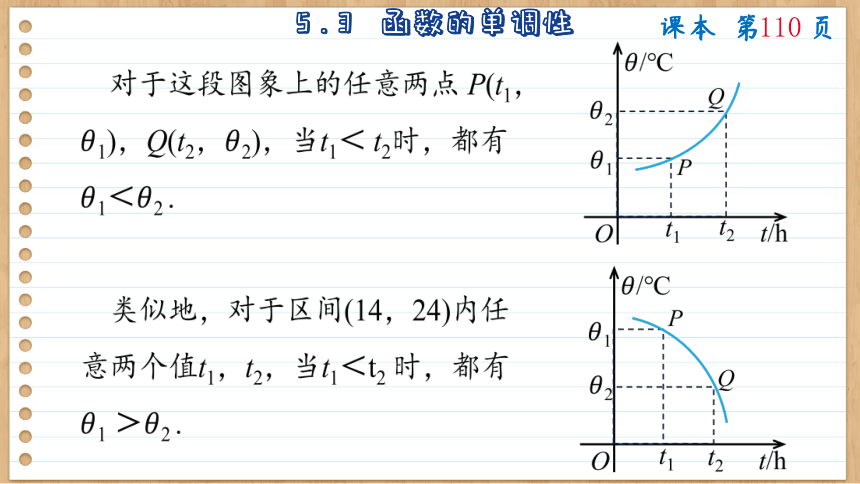
对于这段图象上的任意两点 P(t1,1),Q(t2,2),当t1< t2时,都有1<2 .
类似地,对于区间(14,24)内任意两个值t1,t2,当t1<t2 时,都有1 >2 .
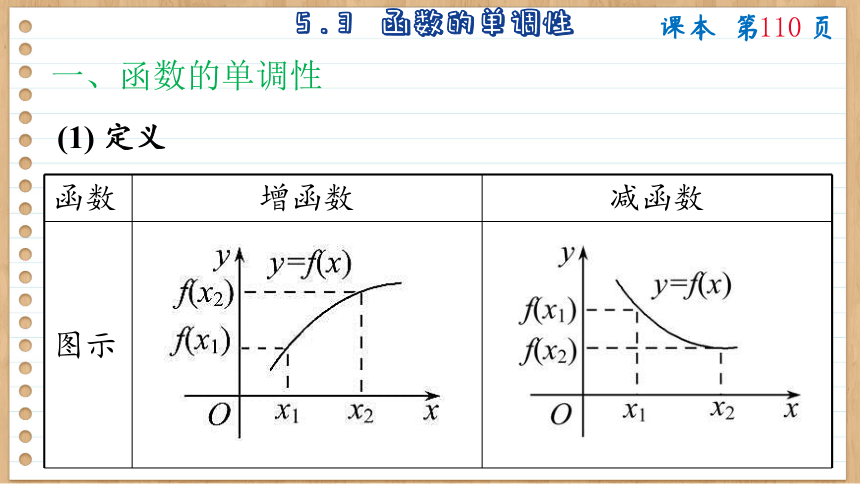
一、函数的单调性
函数 增函数 减函数
图示
(1) 定义
函数 增函数 减函数
条件 设函数 y=f(x) 的定义域为A,区间 I A.如果对于区间 I 内的任意两个值x1,x2,当x1<x2时,
都有___________ 都有___________
结论 (1)y=f(x)在区间I上是___________ (2)I称为y=f(x)的增区间 (1)y=f(x)在区间I上是____________
(2)I称为y=f(x)的减区间
f(x1)<f(x2)
f(x1)>f(x2)
增函数
减函数
(2)本质:
函数的单调性反映的是两个变量的对应变换规律,定量地刻画了函数在区间上图象的变化趋势,是函数诸多性质中最核心、最本质的性质.
(3)应用:证明函数的单调性、比较大小、解不等式、
求参数范围等.
【思考】
函数单调性的定义中,能否将“任意”改为“存在”
提示:不能,
一些特殊的值满足并不能说明函数的单调性.
二、单调性与单调区间
如果函数 y=f(x) 在区间 I 上是增函数或减函数,那么称函数 y=f(x) 在区间 I 上具有单调性.
增区间和减区间统称为单调区间.
【思考】
函数 y=f(x) 在定义域内的每一个区间 D1,D2,…上都单调递减,那么函数在定义域上是减函数吗 你能举例说明吗
提示:不是.如函数 y= 在(-∞,0),(0, +∞)上都单调递减,但在定义域上不具有单调性.
例 1
画出下列函数图象,并写出单调区间:
(1) y=-x2+2;
解:函数图象如图,
增区间为(-∞ ,0],
减区间为[0,+∞).
(2) y= (x≠0).
解:函数图象如图,
(-∞,0)和(0,+∞)
是两个减区间.
例 2
证明:
函数 f(x)=--1在区间(-∞,0)上是增函数.
证明 设 x1,x2 为区间(-∞,0)上的任意两个值,
且 x1<x2,则 x1-x2<0,x1x2>0.
因为 f(x1)-f(x2) =(--1)-(--1)
= - =.
所以 f(x1) - f(x2) < 0,
即 f(x1) < f(x2).
故 f(x)=--1在区间(-∞ ,0) 上是增函数.
记 y2-y1= y,x2-x1= x,那么函数的单调性与 的符号有什么关系
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 函数f(x)=x2,因为-1<2,且f(-1)<f(2),则函数
是增函数. ( )
(2) 函数f(x)=在(-∞,0)∪(0,+∞)上是减函数. ( )
(3) 函数f(x)在某一区间D上要么是增函数要么是减函数.
( )
2. 函数 y=f(x) 的图象如图所示,其减区间是 ( )
A.[-4,4]
B.[-4,-3]∪[1,4]
C.[-3,1]
D.[-4,-3],[1,4]
D
解析:由图象知函数在[-4,-3]以及[1,4]上是减函数,则对应的减区间为[-4,-3],[1,4].
解析
3. 若函数 f(x)=(2k-1)x+1 是减函数,则实数 k 的取值
范围是______________.
(-∞,)
解析:由题意知,2k-1<0,解得 k< .
解析
【课堂检测·素养达标】
1. 函数 y=∣x∣-1的减区间为 ( )
A. (0,+∞) B.(-∞,0)
C. (-∞,-1) D.(-1,+∞)
B
解析:当x≥0时,y=∣x∣-1=x-1,此时函数为增函数,
当x<0时,y=∣x∣-1=-x-1,此时函数为减函数,
即函数的减区间为(-∞,0).
解析
2. 函数 y=f(x) 的图象如图所示,则 f(x)的减区间是 ( )
A. (0,1) B. (-∞,1)
C. (,2) D. (-∞,3)
A
解析:由图象可知减区间为(0,1).
解析
3. 函数 y=在 (0,+∞) 上是增函数,则 k 的取值
范围是 ( )
A. k≥1 B. k≤1 C. k>1 D. k<1
D
解析:k-1>0时,由y=可知,在区间(-∞,0),(0,+∞)上是减函数,不合题意;
当k-1<0时,由y=可知,在区间(-∞,0),(0,+∞)上是增函数,故k<1.
解析
4. 若 f(x) 是减函数,且 f(3x-2)<f(3),则 x 的取值范围
是________________.
( ,+∞)
解析:函数的定义域为R. 由条件可知,3x-2>3,
解得 x> .
解析
解析:函数 f(x) =2x2-3∣x∣=
的图象如图所示,故它的增区间为[-,0],[,+∞) .
2x2-3,x≥0,
2x2+3,x<0.
5. 函数 f(x) =2x2-3∣x∣的增区间是
_______________________.
[-,0],[,+∞)
解析
在图中,我们从图象上看出 14 时的气温为全天的最高气温,它表示在0~24 时,气温于14 时达到最大值.从中可以看出,图象在这一点的位置最高.
在图中,可以看出对于任意的 x∈R,都有
f(x)<2=f(0).
三、函数的最大值和最小值
(1) 定义:
条件 设y=f(x)的定义域为A,如果存在 x0∈A,使得对于任意的x∈A,都有
前提 f(x)≤f(x0) f(x)≥f(x0)
结论 称f(x0)为y=f(x)的最大值,记为ymax=f(x0) 称f(x0)为y=f(x)的最小值,记为_________
ymin=f(x0)
(2)本质:
函数图象上最高点的纵坐标即为最大值;最低点的纵坐标即为最小值.
(3)应用:
求函数的值域,参数的范围,解决实际问题.
【思考】
函数 f(x)=-x2 的定义域为R,存在实数1,对于任意x∈R,都有f(x)≤1.那么1是函数 f(x)=-x2的最大值吗 为什么
提示:不是.
因为不存在 x0∈R,使得 f(x0) =-x02=1.
例 3
图5-3-4 为函数 y=f(x),x∈[-4,7]的图象,指出它的最大值、最小值及单调区间.
解 观察函数图象可以知道,图象上位置最高的点是 (3,3),最低的点是(-1.5,-2).
因此,当x=3时,函数y=f(x)取得最大值,即ymax=3;当x=-1.5时,函数y=f(x)取得最小值,即ymin=-2.
函数的增区间为[-1.5,3],[5,6];
减区间为[- 4,-1.5],[3,5],[6,7].
例 4
求下列函数的最小值:
(1) y=x2-2x;
解:因为 y=x2-2x = (x-1)2-1>-1,
且当x=1时 y=-1.
所以函数在 x=1时取得最小值-1,
即 ymin=-1.
(2) y=,x∈[1,3].
解 因为对于任意实数 x∈ [1,3],都有≥ ,
且当 x=3 时=.
所以函数在 x=3 时取得最小值,即 ymin=.
思 考
例 4中的两个函数有无最大值
例 5
已知函数y=f(x)的定义域是[a,b],a<c<b. 在区间[a,c] 上,f(x)单调递增;在区间[c,b] 上,f(x)单调递减,试证明 f(x) 在 x=c 时取得最大值.
证明 因为在区间[a,c] 上,f(a)单调递增,
所以对于任意 x∈ [a,c],都有 f(x) < f(c).
又因为在区间[c,b] 上,f(x)单调递减,
所以对于任意 x∈[c,b],都有 f(x)≤f(c).
因此,对于任意 x∈[a,b]都有 f(x)≤f(c),即f(x)在 x=c 时取得最大值.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1)任何函数都有最大值、最小值. ( )
(2)如果一个函数有最大值,那么最大值是唯一的. ( )
(3)如果一个函数f(x)在区间[a,b]上单调递减,那么函数的最大值是f(b). ( )
2. 函数 f(x)=x2-3x(∣x∣<1) ( )
A.有最大值,但无最小值
B.有最大值,也有最小值
C.无最大值,但有最小值
D.既无最大值,也无最小值
D
解析:f(x)=x2-3x是开口向上的抛物线,其对称轴方程为x=,则函数f(x)在(-1,1)上单调递减,所以函数f(x)=x2 -3x(|x|<1)既无最大值,也无最小值.
解析
3. 函数 y= 在区间[2,6]上的最大值、最小值分别是
( )
A.1, B. ,1 C. , D. ,
A
解析:因为 y= 在区间[2,6]上单调递减,
所以当 x=2 时取最大值 y=1;
当 x=6 时取最小值 y= .
解析
【跟踪训练】
1. 函数 y= 在 [2,3] 上的最小值为 ( )
A.1 B. C. D. -
B
解析:y= 在 [2,3] 上为减函数,
所以 x=3 时取最小值为.
解析
2. 函数f(x)的图象如图,则其最大值、最小值分别为
( )
A. f(), f(-) B. f(0),f()
C. f(-) ,f(0) D. f(0),f(3)
B
解析:观察函数图象,f(x)的最大值、最小值分别为f(0), f().
解析
解析:函数 y= 的图象如图:
由图象可得函数的最大值是4.
x+3,(x≤1),
-x+5,(x>1),
3. 函数 y= 的最大值是( )
A.3 B.4 C.5 D.6
x+3,(x≤1),
-x+5,(x>1),
B
解析
4.当0≤x≤2时,a<-x2+2x恒成立,则实数a的取值范围是 ( )
A.(-∞,1] B.(-∞,0]
C.(-∞,0) D.(0,+∞)
C
解析:令 f(x)=-x2+2x,则 f(x)=-x2+2x=-(x-1)2+1.
又因为x∈[0,2],所以f(x)min=f(0)=f(2)=0.所以a<0.
解析
5. 函数 f(x)=在[1,b](b>1)上的最小值是 ,则
b=______.
4
解析:因为 f(x) 在 [1,b] 上为减函数,所以 f(x) 在 [1,b] 上的最小值为 f(b)==,所以b=4.
解析
练 习
1. 判断函数f(x)=x2-1在(0,+∞)上是增函数还是减函数.
增函数
证明 在(0, +∞)上任取两个不相等的实数 x1,x2,
且设 x1 <x2;
则 f(x1)-f(x2)=(x12-1)-(x22-1)=x12-x22
=(x1+x2)(x1- x2),
∵0<x1<x2,∴ x1-x2<0,x1+x2>0,
∴ f(x1)-f(x2)<0,∴ f(x1) < f(x2).
∴函数 f(x)=x2-1在(0,+∞)上是增函数.
2. 画出函数 f(x)=∣x+1∣的图象,并根据图象写出f(x)
的单调区间.
解 函数 f(x)=∣x+1∣= ,
函数图象如下图所示,
由图象可知,函数 f(x) 的单调递增区间为[-1, +∞),单调递减区间为(-∞,-1].
x+1,x≥-1
-x-1,x<-1
3. 判断函数 f(x)=-x2+2x 在(-∞ ,0)上是增函数还是
减函数.
函数 f(x)=-x2+2 在(-∞,0)上是增函数.
证明如下:设在(-∞,0) 上任意取 x1,x2,且x1<x2,
∴ f(x1)-f(x2)=(-x12+2x1)-(-x22+2x2)
=(x22-x12)+(2x1-2x2)
=(x2-x1)(x1+x2)+(2x1-2x2)
=(x2-x1)(x1+x2-2),
∵ x1<x2<0,
∴ x2-x1>0,x1+x2<0,
∴ x1+x2-2<0,
∴(x2-x1)(x1+x2-2)<0,
∴f(x1)-f(x2)<0,
∴f(x1)<f(x2),
∴函数 f(x)=-x2+2x 在 (-∞,0) 上是增函数.
4. 求函数 f(x)=-x2+2x 在[0,10]上的最大值和最小值.
解 f(x)=-x2+2x-1+1=- (x-1)2+1,
对称轴x=1,
∴函数f(x)在[0,1)递增,在(1,10]递减,
∴f(x)max=1,f(x)min=f(10) =-80.
5. 函数y=在区间(-2,-1]上有最大值吗 有最小值吗
解 由题意可得:y′=-<0,
∴当x∈(-2,-1]时,函数 y= 在区间(-2,-1]上单调递减,
∴ y不存在最大值;x=-1时,y取得最小值,ymin=-1,
∴ y=在区间(-2,1]上无最大值,最小值为-1.
6. 证明:函数f(x)=-2x+1是减函数.
解 由题,f(x)=-2x+1,x ∈ R,
因为f′(x)=-2< 0,
所以函数 f(x)=-2x+1为减函数.
7. 下图分别为函数 y=f(x) 和 y=g(x) 的图象,试写出函
数 y=f(x) 和 y=g(x) 的增区间.
解
根据函数单调性的定义,函数在单调递增区间上图像呈上升趋势,由函数图像可得:
函数 y=f(x) 的单调增区间是[1,4) 和[4,6];
函数 y=g(x) 的单调增区间是[-,0]和[,3π].
8. 判断下列说法是否正确:
(1) 若定义在 R 上的函数 f(x) 满足 f(2)> f(1),则数f(x)
是 R 上的增函数;
解 若函数f(x)在R上为增函数,则对于任意的 x1,x2∈R 且x1 <x2,则 f(x1)<f(x2) 一定成立,
若f(2)>f(1)成立,f(2)>f(0)不一定成立,函数f(x)在R上不一定是增函数,(1)错误;
(2) 若定义在 R 上的函数 f(x) 满 f(2)>f(1),则函数 f(x)
在 R 上不是减函数;
解 若函数f(x)在R上为减函数,则对于任意的x1,x2∈R 且x1 <x2,则f(x1)>f(x2) 一定成立,所以,f(2)<f(1)一定成立,
所以,若 f(2)>f(1),函数f(x)在R上一定不是减函数,(2)正确;
(3) 若定义在 R 上的函数f(x)在区间(-∞ ,0] 上单调递增,
在区间[0,+∞) 上也单调递增,则函数 f(x)在 R 上是
增函数;
解 若定义在R上的函数f(x)在区间(-∞ ,0]上是增函数,
在区间[0,+∞)上也是增函数,则满足对于任意的 x1,x2∈R且x1<x2,则f(x1)<f(x2)成立,
所以,函数f(x)在R上是增函数,(3)正确;
(4) 若定义在 R 上的函数 f(x)在区间(-∞ ,0] 上单调递增,
在区间(0,+∞)上也单调递增,则函数 f(x) 在 R 上是
增函数.
解 设函数 f(x)= ,是定义在R上的函数,且f(x)在区间(-∞ ,0]上是增函数,在区间(0,+∞)上也是增函数,而-1<1,但 f(-1)=f(1),不符合增函数的定义,所以,函数f(x)在R上是不是增函数,(4)错误.
-x+1,x≤0
x-1,x>0
习题 5.3
感受·理解
1. 已知 k,b 是常数,填写下表:
函数 y=kx+b y=
k>0 k<0 k>0 k<0
单调区间 (-∞,+∞) (-∞,+∞) (-∞,0),(0,+∞) (-∞,0),(0,+∞)
单 调 性 单调增函数 单调减函数 在每个区间内单调递减 在每个区间内单调递增
2. 指出下列函数的单调区间:
(1) y=1-3x;
解 ∵k=-3<0.
∴y=1-3x 在(-∞,+∞)单调递减;
解 函数 y=+2的定义域为(-∞ ,0)∪(0,+∞),
∴y= 在(-∞,0),(0,+∞)单调递减,
∴函数 y= +2 在(-∞,0),(0,+∞)单调递减;
(2) y= +2
(3) y=x2+1;
解 函数 y=x2+1定义域为R,
∵ y=x2在(-∞,0) 单调递减,
在(0,+∞)单调递增,
∴ y=x2+1在(-∞,0) 单调递减,
在(0,+∞)单调递增;
(4) y=-x2+x-1.
解 ∵y=-x2+x-1的定义域为R,
函数图象的对称轴为 x=,图象开口向下,
∴函数 y=-x2+x-1 在(-∞,)单调递增,
在(,+∞)单调递减.
3. 画出下列函数的图象,指出函数的单调区间,并求出
函数的最大值或最小值:
(1) f(x) =-x2-1;
解 函数图象如图(1),增区间为(-∞,0],减区间为[0, +∞),最大值为-1,无最小值.
(2) f(x)= x2-2x-1,x∈[-1,1];
解 函数图象如图(2),减区间为[-1,1],
最大值为 2,最小值为 -2.
(3) f(x) = x∣x∣;
解 f(x) = 函数图象如图(3),
增区间为(-∞,+∞),
既无最大值,也无最小值.
x2,x≥0,
- x2,x<0,
(4) f(x)=-2;
解 函数图象如图(4),
减区间为[0,+∞),
最大值为 ,无最小值.
(5) f(x)=
x-2,x≥0,
-x-2,x<0;
解 函数图象如图(5),增区间为[0,+∞),
减区间为(-∞ ,0],
无最大值,最小值为-2.
(6) f(x)=
x2+2x-1,x∈[0,+∞)
-x2+2x-1,x∈[-∞,0).
解 函数图象如图(6),
增区间为(-∞,+∞),
既无最大值,也无最小值.
4. 设 a 为实数,已知函数 y=f(x) 在定义域 R 上是减函数,
f(a+1) >f(2a),求 a 的取值范围.
解 由题意可知,f(x)在R上是减函数.
∴ f(a+1)>f(2a),
∴ a+1<2a,
解得 a>1.
5. 证明:
(1) 函数 f(x)=-2x2+3 在区间(-∞,0]上是增函数;
解 设 x1,x2∈(-∞ ,0],且 x1<x2,
则f(x1)-f(x2)=-2x12+2x22
= 2(x2+x1)(x2-x1),
∵ x1,x2∈(-∞,0],且 x1<x2,
∴ x1+x2<0,x2-x1>0,
∴ 2(x2+x1)(x2-x1)<0,
即 f(x1)-f(x2)<0,
即 f(x1)<f(x2),
∴ f(x) 在区间 (-∞,0] 上是增函数.
(2) 函数 f(x)=-x+1 在区间(-∞,0]上是减函数;
解 设 x1,x2∈(-∞,0],且 x1<x2,
则 f(x1)-f(x2) =-x13+x23 =(x2-x1)(x22+x1x2+x12),
∵ x1<x2≤0,∴x2-x1>0,
x22+x1x2+x12 =(x2+x1)2+x12>0
∴ f(x1)-f(x2)>0,即 f(x1)>f(x2),
∴ f(x)在区间(-∞,0]上是减函数.
(3) 函数 f(x)=2- 在区间(-∞ ,0)和(0, +∞) 上都是
增函数.
解 设 x1<x2<0,则 f(x1)-f(x2) =-+=,
∵x1<x2< 0,
∴ x1-x2<0, x1x2 >0,
∴ f(x1)<f(x2),
∴ f(x)在区间(-∞,0)上是增函数,
设 0<x1<x2 则 f(x1)-f(x2) =-+=,
∵ 0<x1<x2
∴ x1-x2<0, x1x2>0.
∴ f(x1) < f(x2)
则 f(x) 在区间 (0,+∞) 上是增函数.
思考·运用
6. 证明:函数 f(x)=2x3-在区间(0,+∞)上是增函数.
证明:任取 0<x1<x2,
则 x1-x2<0,x1x2>0.
因为 f(x1)-f(x2)=2x13--(2x23- )
=2(x13-x23)+
=2(x1-x2)(x12+x1x2+x22)+,
=(x1-x2)[2(x12+x1x2+x22) + ].
所以 f(x1)-f(x2)<0,所以 f(x1)<f(x1),
故 f(x)=2x3- 在区间 (0,+∞) 上是增函数.
7. 已知函数 f(x)=x+,x∈(0,+∞)
(1) 求证:f(x)在区间(0,1]上单调递减,在区间[1,+∞)
上单调递增;
证明:∵ f(x)=x+,
∴ f′(x)=1-= ,
∴当 x∈(0,1) 时, f′(x)< 0,
当 x∈(1, +∞) 时, f′(x) >0,
∴ f(x)在区间(0,1]上是单调减函数,在区间[1, +∞) 上是单调增函数;
(2) 试求函数 f(x) 的最大值或最小值.
证明: 由 (1) 知,f(x)有最小值,无最大值;
fmin(x)=f(1)=1+1=2.
探究·拓展
8. 利用技术工具 (如计算器或计算机) 画函数
f(x)=x3-3x+1的图象并求函数的单调区间.
函数 f(x)=x3-3x+1图象如下:
因为 f(x)=x3-3x+1,
所以 f′(x)=3x2-3=3(x-1)(x+1).
由 f′(x)>0得x>1或x<-1,
所以 f(x)=x3-3x+1的单调递增区间为
(-8,-1),(1,+∞),
由f′(x)<0得-1<x<1,
所以f(x)=x3-3x+1的单调递增区间为(-1,1).
本课结束
This lesson is over
THANKS!
第5章
函数概念与性质
5 . 3
函数的单调性
在 5.1节开头的第三个问题中,气温是关于时间 t 的函数,记为=f(t).观察这个气温变化图(如图 5-3-1),说出气温在哪些时段内是逐渐升高的,在哪些时段内是逐渐下降的.
● 怎样用数学语言刻画上述某一时段内“随着时间的增加气温逐渐升高”这一特征
由图可知,从4时到14 时这一时间段内,图象是上升趋势,气温逐渐升高.
对于这段图象上的任意两点 P(t1,1),Q(t2,2),当t1< t2时,都有1<2 .
类似地,对于区间(14,24)内任意两个值t1,t2,当t1<t2 时,都有1 >2 .
一、函数的单调性
函数 增函数 减函数
图示
(1) 定义
函数 增函数 减函数
条件 设函数 y=f(x) 的定义域为A,区间 I A.如果对于区间 I 内的任意两个值x1,x2,当x1<x2时,
都有___________ 都有___________
结论 (1)y=f(x)在区间I上是___________ (2)I称为y=f(x)的增区间 (1)y=f(x)在区间I上是____________
(2)I称为y=f(x)的减区间
f(x1)<f(x2)
f(x1)>f(x2)
增函数
减函数
(2)本质:
函数的单调性反映的是两个变量的对应变换规律,定量地刻画了函数在区间上图象的变化趋势,是函数诸多性质中最核心、最本质的性质.
(3)应用:证明函数的单调性、比较大小、解不等式、
求参数范围等.
【思考】
函数单调性的定义中,能否将“任意”改为“存在”
提示:不能,
一些特殊的值满足并不能说明函数的单调性.
二、单调性与单调区间
如果函数 y=f(x) 在区间 I 上是增函数或减函数,那么称函数 y=f(x) 在区间 I 上具有单调性.
增区间和减区间统称为单调区间.
【思考】
函数 y=f(x) 在定义域内的每一个区间 D1,D2,…上都单调递减,那么函数在定义域上是减函数吗 你能举例说明吗
提示:不是.如函数 y= 在(-∞,0),(0, +∞)上都单调递减,但在定义域上不具有单调性.
例 1
画出下列函数图象,并写出单调区间:
(1) y=-x2+2;
解:函数图象如图,
增区间为(-∞ ,0],
减区间为[0,+∞).
(2) y= (x≠0).
解:函数图象如图,
(-∞,0)和(0,+∞)
是两个减区间.
例 2
证明:
函数 f(x)=--1在区间(-∞,0)上是增函数.
证明 设 x1,x2 为区间(-∞,0)上的任意两个值,
且 x1<x2,则 x1-x2<0,x1x2>0.
因为 f(x1)-f(x2) =(--1)-(--1)
= - =.
所以 f(x1) - f(x2) < 0,
即 f(x1) < f(x2).
故 f(x)=--1在区间(-∞ ,0) 上是增函数.
记 y2-y1= y,x2-x1= x,那么函数的单调性与 的符号有什么关系
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 函数f(x)=x2,因为-1<2,且f(-1)<f(2),则函数
是增函数. ( )
(2) 函数f(x)=在(-∞,0)∪(0,+∞)上是减函数. ( )
(3) 函数f(x)在某一区间D上要么是增函数要么是减函数.
( )
2. 函数 y=f(x) 的图象如图所示,其减区间是 ( )
A.[-4,4]
B.[-4,-3]∪[1,4]
C.[-3,1]
D.[-4,-3],[1,4]
D
解析:由图象知函数在[-4,-3]以及[1,4]上是减函数,则对应的减区间为[-4,-3],[1,4].
解析
3. 若函数 f(x)=(2k-1)x+1 是减函数,则实数 k 的取值
范围是______________.
(-∞,)
解析:由题意知,2k-1<0,解得 k< .
解析
【课堂检测·素养达标】
1. 函数 y=∣x∣-1的减区间为 ( )
A. (0,+∞) B.(-∞,0)
C. (-∞,-1) D.(-1,+∞)
B
解析:当x≥0时,y=∣x∣-1=x-1,此时函数为增函数,
当x<0时,y=∣x∣-1=-x-1,此时函数为减函数,
即函数的减区间为(-∞,0).
解析
2. 函数 y=f(x) 的图象如图所示,则 f(x)的减区间是 ( )
A. (0,1) B. (-∞,1)
C. (,2) D. (-∞,3)
A
解析:由图象可知减区间为(0,1).
解析
3. 函数 y=在 (0,+∞) 上是增函数,则 k 的取值
范围是 ( )
A. k≥1 B. k≤1 C. k>1 D. k<1
D
解析:k-1>0时,由y=可知,在区间(-∞,0),(0,+∞)上是减函数,不合题意;
当k-1<0时,由y=可知,在区间(-∞,0),(0,+∞)上是增函数,故k<1.
解析
4. 若 f(x) 是减函数,且 f(3x-2)<f(3),则 x 的取值范围
是________________.
( ,+∞)
解析:函数的定义域为R. 由条件可知,3x-2>3,
解得 x> .
解析
解析:函数 f(x) =2x2-3∣x∣=
的图象如图所示,故它的增区间为[-,0],[,+∞) .
2x2-3,x≥0,
2x2+3,x<0.
5. 函数 f(x) =2x2-3∣x∣的增区间是
_______________________.
[-,0],[,+∞)
解析
在图中,我们从图象上看出 14 时的气温为全天的最高气温,它表示在0~24 时,气温于14 时达到最大值.从中可以看出,图象在这一点的位置最高.
在图中,可以看出对于任意的 x∈R,都有
f(x)<2=f(0).
三、函数的最大值和最小值
(1) 定义:
条件 设y=f(x)的定义域为A,如果存在 x0∈A,使得对于任意的x∈A,都有
前提 f(x)≤f(x0) f(x)≥f(x0)
结论 称f(x0)为y=f(x)的最大值,记为ymax=f(x0) 称f(x0)为y=f(x)的最小值,记为_________
ymin=f(x0)
(2)本质:
函数图象上最高点的纵坐标即为最大值;最低点的纵坐标即为最小值.
(3)应用:
求函数的值域,参数的范围,解决实际问题.
【思考】
函数 f(x)=-x2 的定义域为R,存在实数1,对于任意x∈R,都有f(x)≤1.那么1是函数 f(x)=-x2的最大值吗 为什么
提示:不是.
因为不存在 x0∈R,使得 f(x0) =-x02=1.
例 3
图5-3-4 为函数 y=f(x),x∈[-4,7]的图象,指出它的最大值、最小值及单调区间.
解 观察函数图象可以知道,图象上位置最高的点是 (3,3),最低的点是(-1.5,-2).
因此,当x=3时,函数y=f(x)取得最大值,即ymax=3;当x=-1.5时,函数y=f(x)取得最小值,即ymin=-2.
函数的增区间为[-1.5,3],[5,6];
减区间为[- 4,-1.5],[3,5],[6,7].
例 4
求下列函数的最小值:
(1) y=x2-2x;
解:因为 y=x2-2x = (x-1)2-1>-1,
且当x=1时 y=-1.
所以函数在 x=1时取得最小值-1,
即 ymin=-1.
(2) y=,x∈[1,3].
解 因为对于任意实数 x∈ [1,3],都有≥ ,
且当 x=3 时=.
所以函数在 x=3 时取得最小值,即 ymin=.
思 考
例 4中的两个函数有无最大值
例 5
已知函数y=f(x)的定义域是[a,b],a<c<b. 在区间[a,c] 上,f(x)单调递增;在区间[c,b] 上,f(x)单调递减,试证明 f(x) 在 x=c 时取得最大值.
证明 因为在区间[a,c] 上,f(a)单调递增,
所以对于任意 x∈ [a,c],都有 f(x) < f(c).
又因为在区间[c,b] 上,f(x)单调递减,
所以对于任意 x∈[c,b],都有 f(x)≤f(c).
因此,对于任意 x∈[a,b]都有 f(x)≤f(c),即f(x)在 x=c 时取得最大值.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1)任何函数都有最大值、最小值. ( )
(2)如果一个函数有最大值,那么最大值是唯一的. ( )
(3)如果一个函数f(x)在区间[a,b]上单调递减,那么函数的最大值是f(b). ( )
2. 函数 f(x)=x2-3x(∣x∣<1) ( )
A.有最大值,但无最小值
B.有最大值,也有最小值
C.无最大值,但有最小值
D.既无最大值,也无最小值
D
解析:f(x)=x2-3x是开口向上的抛物线,其对称轴方程为x=,则函数f(x)在(-1,1)上单调递减,所以函数f(x)=x2 -3x(|x|<1)既无最大值,也无最小值.
解析
3. 函数 y= 在区间[2,6]上的最大值、最小值分别是
( )
A.1, B. ,1 C. , D. ,
A
解析:因为 y= 在区间[2,6]上单调递减,
所以当 x=2 时取最大值 y=1;
当 x=6 时取最小值 y= .
解析
【跟踪训练】
1. 函数 y= 在 [2,3] 上的最小值为 ( )
A.1 B. C. D. -
B
解析:y= 在 [2,3] 上为减函数,
所以 x=3 时取最小值为.
解析
2. 函数f(x)的图象如图,则其最大值、最小值分别为
( )
A. f(), f(-) B. f(0),f()
C. f(-) ,f(0) D. f(0),f(3)
B
解析:观察函数图象,f(x)的最大值、最小值分别为f(0), f().
解析
解析:函数 y= 的图象如图:
由图象可得函数的最大值是4.
x+3,(x≤1),
-x+5,(x>1),
3. 函数 y= 的最大值是( )
A.3 B.4 C.5 D.6
x+3,(x≤1),
-x+5,(x>1),
B
解析
4.当0≤x≤2时,a<-x2+2x恒成立,则实数a的取值范围是 ( )
A.(-∞,1] B.(-∞,0]
C.(-∞,0) D.(0,+∞)
C
解析:令 f(x)=-x2+2x,则 f(x)=-x2+2x=-(x-1)2+1.
又因为x∈[0,2],所以f(x)min=f(0)=f(2)=0.所以a<0.
解析
5. 函数 f(x)=在[1,b](b>1)上的最小值是 ,则
b=______.
4
解析:因为 f(x) 在 [1,b] 上为减函数,所以 f(x) 在 [1,b] 上的最小值为 f(b)==,所以b=4.
解析
练 习
1. 判断函数f(x)=x2-1在(0,+∞)上是增函数还是减函数.
增函数
证明 在(0, +∞)上任取两个不相等的实数 x1,x2,
且设 x1 <x2;
则 f(x1)-f(x2)=(x12-1)-(x22-1)=x12-x22
=(x1+x2)(x1- x2),
∵0<x1<x2,∴ x1-x2<0,x1+x2>0,
∴ f(x1)-f(x2)<0,∴ f(x1) < f(x2).
∴函数 f(x)=x2-1在(0,+∞)上是增函数.
2. 画出函数 f(x)=∣x+1∣的图象,并根据图象写出f(x)
的单调区间.
解 函数 f(x)=∣x+1∣= ,
函数图象如下图所示,
由图象可知,函数 f(x) 的单调递增区间为[-1, +∞),单调递减区间为(-∞,-1].
x+1,x≥-1
-x-1,x<-1
3. 判断函数 f(x)=-x2+2x 在(-∞ ,0)上是增函数还是
减函数.
函数 f(x)=-x2+2 在(-∞,0)上是增函数.
证明如下:设在(-∞,0) 上任意取 x1,x2,且x1<x2,
∴ f(x1)-f(x2)=(-x12+2x1)-(-x22+2x2)
=(x22-x12)+(2x1-2x2)
=(x2-x1)(x1+x2)+(2x1-2x2)
=(x2-x1)(x1+x2-2),
∵ x1<x2<0,
∴ x2-x1>0,x1+x2<0,
∴ x1+x2-2<0,
∴(x2-x1)(x1+x2-2)<0,
∴f(x1)-f(x2)<0,
∴f(x1)<f(x2),
∴函数 f(x)=-x2+2x 在 (-∞,0) 上是增函数.
4. 求函数 f(x)=-x2+2x 在[0,10]上的最大值和最小值.
解 f(x)=-x2+2x-1+1=- (x-1)2+1,
对称轴x=1,
∴函数f(x)在[0,1)递增,在(1,10]递减,
∴f(x)max=1,f(x)min=f(10) =-80.
5. 函数y=在区间(-2,-1]上有最大值吗 有最小值吗
解 由题意可得:y′=-<0,
∴当x∈(-2,-1]时,函数 y= 在区间(-2,-1]上单调递减,
∴ y不存在最大值;x=-1时,y取得最小值,ymin=-1,
∴ y=在区间(-2,1]上无最大值,最小值为-1.
6. 证明:函数f(x)=-2x+1是减函数.
解 由题,f(x)=-2x+1,x ∈ R,
因为f′(x)=-2< 0,
所以函数 f(x)=-2x+1为减函数.
7. 下图分别为函数 y=f(x) 和 y=g(x) 的图象,试写出函
数 y=f(x) 和 y=g(x) 的增区间.
解
根据函数单调性的定义,函数在单调递增区间上图像呈上升趋势,由函数图像可得:
函数 y=f(x) 的单调增区间是[1,4) 和[4,6];
函数 y=g(x) 的单调增区间是[-,0]和[,3π].
8. 判断下列说法是否正确:
(1) 若定义在 R 上的函数 f(x) 满足 f(2)> f(1),则数f(x)
是 R 上的增函数;
解 若函数f(x)在R上为增函数,则对于任意的 x1,x2∈R 且x1 <x2,则 f(x1)<f(x2) 一定成立,
若f(2)>f(1)成立,f(2)>f(0)不一定成立,函数f(x)在R上不一定是增函数,(1)错误;
(2) 若定义在 R 上的函数 f(x) 满 f(2)>f(1),则函数 f(x)
在 R 上不是减函数;
解 若函数f(x)在R上为减函数,则对于任意的x1,x2∈R 且x1 <x2,则f(x1)>f(x2) 一定成立,所以,f(2)<f(1)一定成立,
所以,若 f(2)>f(1),函数f(x)在R上一定不是减函数,(2)正确;
(3) 若定义在 R 上的函数f(x)在区间(-∞ ,0] 上单调递增,
在区间[0,+∞) 上也单调递增,则函数 f(x)在 R 上是
增函数;
解 若定义在R上的函数f(x)在区间(-∞ ,0]上是增函数,
在区间[0,+∞)上也是增函数,则满足对于任意的 x1,x2∈R且x1<x2,则f(x1)<f(x2)成立,
所以,函数f(x)在R上是增函数,(3)正确;
(4) 若定义在 R 上的函数 f(x)在区间(-∞ ,0] 上单调递增,
在区间(0,+∞)上也单调递增,则函数 f(x) 在 R 上是
增函数.
解 设函数 f(x)= ,是定义在R上的函数,且f(x)在区间(-∞ ,0]上是增函数,在区间(0,+∞)上也是增函数,而-1<1,但 f(-1)=f(1),不符合增函数的定义,所以,函数f(x)在R上是不是增函数,(4)错误.
-x+1,x≤0
x-1,x>0
习题 5.3
感受·理解
1. 已知 k,b 是常数,填写下表:
函数 y=kx+b y=
k>0 k<0 k>0 k<0
单调区间 (-∞,+∞) (-∞,+∞) (-∞,0),(0,+∞) (-∞,0),(0,+∞)
单 调 性 单调增函数 单调减函数 在每个区间内单调递减 在每个区间内单调递增
2. 指出下列函数的单调区间:
(1) y=1-3x;
解 ∵k=-3<0.
∴y=1-3x 在(-∞,+∞)单调递减;
解 函数 y=+2的定义域为(-∞ ,0)∪(0,+∞),
∴y= 在(-∞,0),(0,+∞)单调递减,
∴函数 y= +2 在(-∞,0),(0,+∞)单调递减;
(2) y= +2
(3) y=x2+1;
解 函数 y=x2+1定义域为R,
∵ y=x2在(-∞,0) 单调递减,
在(0,+∞)单调递增,
∴ y=x2+1在(-∞,0) 单调递减,
在(0,+∞)单调递增;
(4) y=-x2+x-1.
解 ∵y=-x2+x-1的定义域为R,
函数图象的对称轴为 x=,图象开口向下,
∴函数 y=-x2+x-1 在(-∞,)单调递增,
在(,+∞)单调递减.
3. 画出下列函数的图象,指出函数的单调区间,并求出
函数的最大值或最小值:
(1) f(x) =-x2-1;
解 函数图象如图(1),增区间为(-∞,0],减区间为[0, +∞),最大值为-1,无最小值.
(2) f(x)= x2-2x-1,x∈[-1,1];
解 函数图象如图(2),减区间为[-1,1],
最大值为 2,最小值为 -2.
(3) f(x) = x∣x∣;
解 f(x) = 函数图象如图(3),
增区间为(-∞,+∞),
既无最大值,也无最小值.
x2,x≥0,
- x2,x<0,
(4) f(x)=-2;
解 函数图象如图(4),
减区间为[0,+∞),
最大值为 ,无最小值.
(5) f(x)=
x-2,x≥0,
-x-2,x<0;
解 函数图象如图(5),增区间为[0,+∞),
减区间为(-∞ ,0],
无最大值,最小值为-2.
(6) f(x)=
x2+2x-1,x∈[0,+∞)
-x2+2x-1,x∈[-∞,0).
解 函数图象如图(6),
增区间为(-∞,+∞),
既无最大值,也无最小值.
4. 设 a 为实数,已知函数 y=f(x) 在定义域 R 上是减函数,
f(a+1) >f(2a),求 a 的取值范围.
解 由题意可知,f(x)在R上是减函数.
∴ f(a+1)>f(2a),
∴ a+1<2a,
解得 a>1.
5. 证明:
(1) 函数 f(x)=-2x2+3 在区间(-∞,0]上是增函数;
解 设 x1,x2∈(-∞ ,0],且 x1<x2,
则f(x1)-f(x2)=-2x12+2x22
= 2(x2+x1)(x2-x1),
∵ x1,x2∈(-∞,0],且 x1<x2,
∴ x1+x2<0,x2-x1>0,
∴ 2(x2+x1)(x2-x1)<0,
即 f(x1)-f(x2)<0,
即 f(x1)<f(x2),
∴ f(x) 在区间 (-∞,0] 上是增函数.
(2) 函数 f(x)=-x+1 在区间(-∞,0]上是减函数;
解 设 x1,x2∈(-∞,0],且 x1<x2,
则 f(x1)-f(x2) =-x13+x23 =(x2-x1)(x22+x1x2+x12),
∵ x1<x2≤0,∴x2-x1>0,
x22+x1x2+x12 =(x2+x1)2+x12>0
∴ f(x1)-f(x2)>0,即 f(x1)>f(x2),
∴ f(x)在区间(-∞,0]上是减函数.
(3) 函数 f(x)=2- 在区间(-∞ ,0)和(0, +∞) 上都是
增函数.
解 设 x1<x2<0,则 f(x1)-f(x2) =-+=,
∵x1<x2< 0,
∴ x1-x2<0, x1x2 >0,
∴ f(x1)<f(x2),
∴ f(x)在区间(-∞,0)上是增函数,
设 0<x1<x2 则 f(x1)-f(x2) =-+=,
∵ 0<x1<x2
∴ x1-x2<0, x1x2>0.
∴ f(x1) < f(x2)
则 f(x) 在区间 (0,+∞) 上是增函数.
思考·运用
6. 证明:函数 f(x)=2x3-在区间(0,+∞)上是增函数.
证明:任取 0<x1<x2,
则 x1-x2<0,x1x2>0.
因为 f(x1)-f(x2)=2x13--(2x23- )
=2(x13-x23)+
=2(x1-x2)(x12+x1x2+x22)+,
=(x1-x2)[2(x12+x1x2+x22) + ].
所以 f(x1)-f(x2)<0,所以 f(x1)<f(x1),
故 f(x)=2x3- 在区间 (0,+∞) 上是增函数.
7. 已知函数 f(x)=x+,x∈(0,+∞)
(1) 求证:f(x)在区间(0,1]上单调递减,在区间[1,+∞)
上单调递增;
证明:∵ f(x)=x+,
∴ f′(x)=1-= ,
∴当 x∈(0,1) 时, f′(x)< 0,
当 x∈(1, +∞) 时, f′(x) >0,
∴ f(x)在区间(0,1]上是单调减函数,在区间[1, +∞) 上是单调增函数;
(2) 试求函数 f(x) 的最大值或最小值.
证明: 由 (1) 知,f(x)有最小值,无最大值;
fmin(x)=f(1)=1+1=2.
探究·拓展
8. 利用技术工具 (如计算器或计算机) 画函数
f(x)=x3-3x+1的图象并求函数的单调区间.
函数 f(x)=x3-3x+1图象如下:
因为 f(x)=x3-3x+1,
所以 f′(x)=3x2-3=3(x-1)(x+1).
由 f′(x)>0得x>1或x<-1,
所以 f(x)=x3-3x+1的单调递增区间为
(-8,-1),(1,+∞),
由f′(x)<0得-1<x<1,
所以f(x)=x3-3x+1的单调递增区间为(-1,1).
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
