6.2 指数函数 课件(共102张PPT)
文档属性
| 名称 | 6.2 指数函数 课件(共102张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 66.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 21:41:32 | ||
图片预览









文档简介
(共102张PPT)
第6章
幂函数指数函数和对数函数
6 . 2
指数函数
试考察下列问题:
(1) 在 4.1节研究细胞分裂时,得到函数 y=2x.
(2) 在4.2.2节的例10 中,得到函数y=0.999 879x.
(3) 庄子曰:“一尺之捶,日取其半,万世不竭” (“捶”同“棰”). 设经过的天数为 x (天),木棰剩余的长度为 y (尺),则有 y=()x.
●函数 y=2x,y=0.999 879x,y=()x具有什么共同特征
这些函数的表达式都是指数幂形式,底数为常数,指数为自变量,这样的函数称为指数函数.
庄子,战国中期著名的思想家、哲学家和文学家,是道家学派的主要代表人物之一,主要著作有《庄子》.
一、指数函数
一般地,
函数
y=ax (a>0,a≠1)
叫作指数函数(exponential function),它的定义域是 R .
【思考】
当指数函数的底数 a=0,a=1,a<0时,对自变量 x的取值有何影响
提示:(1) 如果a=0,当x>0时,ax恒等于0,没有研究的必要;当x≤0时,ax无意义.
(2) 如果a<0,例如y=(-4)x,这时对于x=,,该函数无意义.
(3) 如果 a=1,则 y=1x 是一个常量,没有研究的价值.
为了避免上述各种情况,所以规定 a>0,且a≠1.
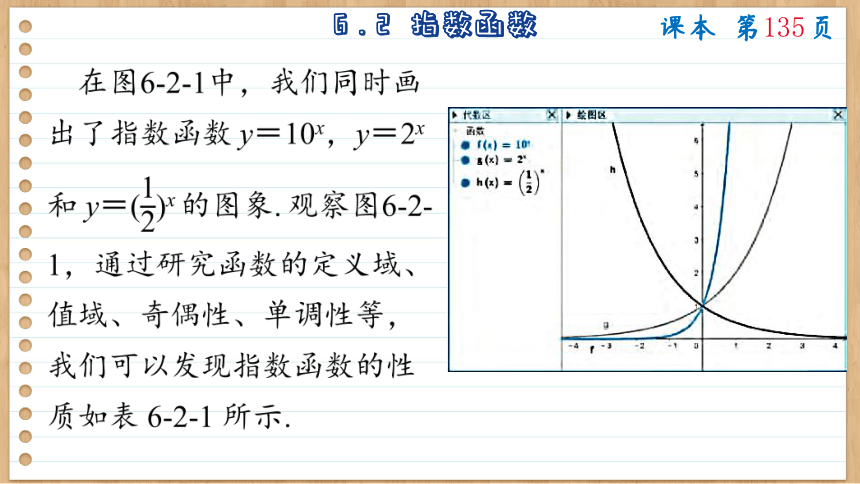
在图6-2-1中,我们同时画出了指数函数 y=10x,y=2x和 y=()x 的图象. 观察图6-2-1,通过研究函数的定义域、值域、奇偶性、单调性等,我们可以发现指数函数的性质如表 6-2-1 所示.
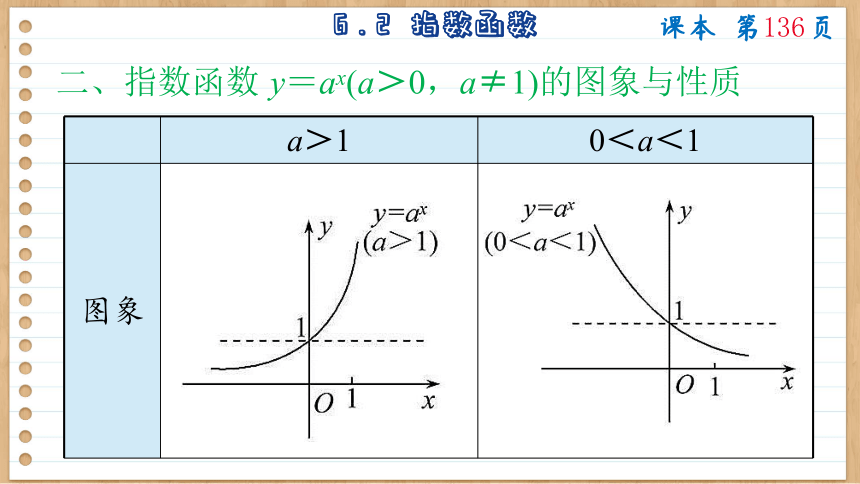
二、指数函数 y=ax(a>0,a≠1)的图象与性质
a>1 0<a<1
图象
a>1 0<a<1
性质 (1) 定义域:________
(2) 值域: ______________
(3) 图象过定点_________,图象在 x 轴上方
(4)在(-∞,+∞) 上是增函数; 当x>0时,y>1; 当x<0时,0<y<1. 在(-∞,+∞)上是减函数;
当x>0时,0<y<1;
当x<0时,y>1.
R
(0,+∞)
(0,1)
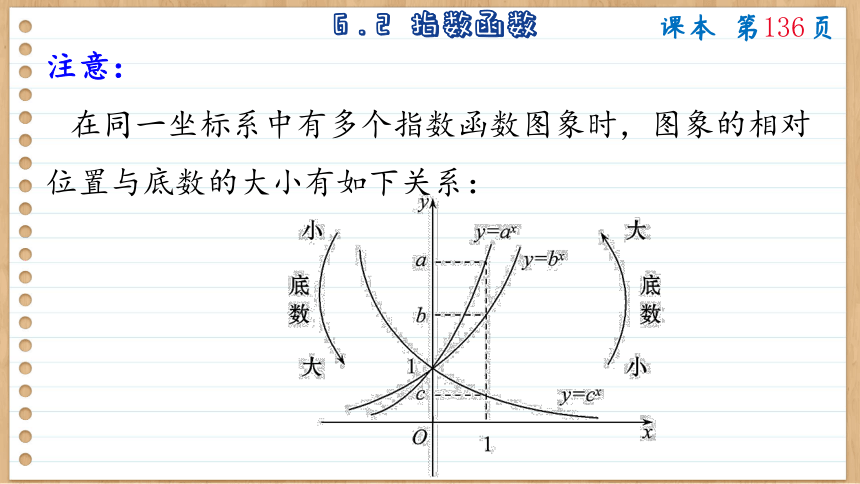
注意:
在同一坐标系中有多个指数函数图象时,图象的相对位置与底数的大小有如下关系:
① 在y轴右侧,图象从上到下相应的底数由大变小:
② 在y轴左侧,图象从下到上相应的底数由大变小,即无论在y轴的左侧还是右侧,底数按逆时针方向变大.这一性质可通过令x=1时,y的取值去理解.
探 究
(1) 在画图过程中,你还发现了指数函数的其他性质吗
(2) 函数 y=2x与 y=()x的图象有怎样的关系 你能得到更般的结论吗
例 1
比较下列各组数中两个数的大小:
(1) 1.52.5,1.53.2;
解:考察指数函数 y=1.5x.
因为 1.5>1,
所以 y=1.5x在 R 上是增函数.
又因为2.5<3.2,所以 1.52.5<1.53.2.
(2) 0.5-1.2,0.5-1.5;
解:考察指数函数 y=0.5x.
因为 0<0.5<1,
所以 y=0.5x在 R 上是减函数.
又因为 -1.2>-1.5,
所以 0.5-1.2<0.5-1.5.
(3) 1.50.3 ,0.81.2.
解:考察指数函数 y=1.5x.
因为 1.5>1,
所以 y=1.5x在 R 上是增函数.
又因为0.3>0,所以 1.50.3>1.50>1.
同理 0.81.2<0.80=1,
故 1.50.3 > 0.81.2.
例 2
(1) 已知 3x≥30.5,求实数 的取值范围;
解:因为 3 > 1.
所以 指数函数 y=3x 在 R 上是增函数,
由 3x≥30.5 可得 x≥0.5.
故的取值范围为区间 [0.5,+∞).
(2) 已知 0.2x<25,求实数 x的取值范围.
解 因为 0<0.2x<1,
所以指数函数 y=0.2x 在 R 上是减函数,
因为 25 =()-2 = 0.2-2,
所以 0.2x < 0.2-2.
由此可得 x>-2.
故 x 的取值范围为区间(-2,+∞).
例 3
(1) y=2x-2; (2) y=2x+2.
说明下列函数的图象与指数函数 y=2x 的图象的关系并画出它们的示意图:
解 比较函数 y=2x与函数 y=2x-2,y=2x+2的取值关系,
列表如表 6-2-2 所示.
一般地,因为函数 y=2x-2中x=a+2对应的y值与函数 y=2x 中 x=a 对应的 y 值相等,所以将指数函数y=2x 的图象向平移2个单位长度,就得到函数 y=2x-2 的图象.
同样地,因为函数 y=2x+2 中 x=a-2 对应的y值与函数 y=2x 中 x=a 对应的 y 值相等,所以将指数函数y=2x的图象向左平移2个单位长度,就得到函数y=2x+2的图象.
这些函数的图象如图 6-2-2 所示.
思 考
函数 y=ax+h与函数 y=ax (a>0,a≠1,h≠0) 的图象之间有怎样的关系
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) y=x6 是指数函数. ( )
(2) 指数函数的图象都在x轴的上方. ( )
(3) 若指数函数 y=ax 是减函数,则0<a<1. ( )
2. 若函数 f(x)=(a2-3a+3)ax是指数函数,则 ( )
A. a=1或a=2 B. a=1
C. a=2 D. a>0且a≠1
C
解析
a2-3a+3=1,
解析:由指数函数的定义得 解得a=2.
a>0且a≠1,
3. 已知函数 f(x)=3x-()x,则 f(x) ( )
A. 是奇函数,且在R上是增函数
B. 是偶函数,且在R上是增函数
C. 是奇函数,且在R上是减函数
D. 是偶函数,且在R上是减函数
A
4. 函数 y=的定义域是 ( )
A. (-∞,0) B. (-∞,0]
C. [0,+∞) D. (0,+∞)
C
解析:由2x-1≥0得2x≥1,即 x≥0,
所以函数的定义域为[0,+∞).
解析
解析:由已知得 解得
所以 f(x) = ()x+3,
所以 f(-2) =()-2+3=4+3=7.
a=,
b=3,
a-1 +b=5,
a0+b=4,
5. 已知函数 f(x)=ax+b(a>0,且a≠1)经过点(-1,5),
(0,4),则 f(-2)的值为__________.
7
解析
【跟踪训练】
1. 函数 y=(a-2)2ax 是指数函数,则 ( )
A. a=1或a=3 B. a=1
C. a=3 D. a>0且a≠1
C
解析
(a-2)2=1,
解析:由指数函数定义知 解得 a=3.
a>0,且a≠1
2. 当x>0时,指数函数(a-1)x<1 恒成立,则实数 a 的
取值范围是 ( )
A. (2,+∞) B. (1,2)
C. (1,+∞) D. R
B
解析:因为当 x>0 时,(a-1)x<1恒成立,
所以0<a-1<1,即1<a<2.
解析
3. 函数 f(x) =()x 在区间 [-2,2] 上的最小值是 ( )
A. B. - C. 4 D. -4
A
解析:函数 f(x)=()x 在定义域R上单调递减,
所以 f(x) 在区间[-2,2]上的最小值是f(2)=()2= .
解析
4. 已知 a=30.2,b=0.2-3,c=(-3)0.2,则 a,b,c 的大
小关系为 ( )
A. a>b>c B. b>a>c
C. c>a>b D. b>c>a
B
解析:c <0,b=53>3,1<a<3,所以 b>a>c.
解析
5. 已知函数 f(x)=ax(a>0,且a≠1)的图象经过点(2,4),
则a=________,若 a2x+1<a3x-1,则x的取值范围是
____________.
2
x>2
解析:因为 f(x) 的图象经过点(2,4),
所以 a2=4,解得a=2,
若a2x+1<a3x-1,即22x+1<23x-1,
故 2x+1<3x-1,解得x>2.
解析
练 习
1. 下列各数中,哪些大于 1,哪些小于 1
() , () , () ,(0.16)0.2.
-
-
() > ()0=1;
() > ()0=1;
-
() < ()0=1;
-
(0.16)0.2 < (0.16)0=1.
2. 指出下列函数的单调性:
(1) y=5x;
解 ∵ y=5x ,x∈R,
∴根据指数函数的性质,5 > 1,
则函数在R上单调递增.
(2) y=()x;
解 ∵ y=()x ,x∈R,
∴根据指数函数的性质, 0<<1,
则函数在R上单调递增.
(3) y=0.5x;
解 ∵ y=0.5x,x∈R.
∴ 根据指数函数的性质0<0.5<1,
则函数在R上单调递减.
(4) y=-2x.
解 ∵ y=-2x,x∈R.
∴ y′=-2xln2<0 在 R 上恒成立.
则函数在 R 上单调递减.
3. 设 a 为实数如果指数函数 f(x)=(a-1)x是 R 上的减函
数,那么 a 的取值范围是( ).
A. a<2 B. a>2
C. 1<a<2 D. 0<a<1
C
4. 比较下列各组数中两个值的大小关系:
(1) 3.10.5 ,3.12.3 ;
(2) ()-1.5, ()-1.8;
解 ∵ y=3.1x 在 R 上单调递增,0.5<2.3,
∴ 3.10.5<3.12.3.
解 ∵ y=()x 在 R 上单调递增, -1.5>-1.8,
∴ ()-1.5> ()-1.8 .
(4) ()-0.3, ()-0.24;
(3) 0.62,0.63;
解 ∵ y=0.6x 在 R 上单调递减,2<3,
∴ 0.62 < 0.6 3.
解 ∵ y=()x 在 R 上单调递增, -0.3<-0.24,
∴ ()-0.3> ()-0.24 .
(5) 0.53.2,1.32.1;
(6) 2.3-2.5,0.2-0.1.
解 ∵ 0.53.2< 0.50=1,1.32.1>1.30=1,
∴ 0.53.2 < 1.32.1.
解 ∵ 2.3-2.5< 2.30=1,0.2-0.1>0.20=1,
∴ 2.3-2.5 < 0.2-0.1.
5. 分别根据下列条件确定正数 a 与 1 的大小关系:
(1) a < a ;
解 ∵ <,且 a < a ,
∴ 函数 y=ax 公在 R 上是增函数,故 a>1.
(2) a > a ;
解 ∵ >,且 a > a ,
∴ 函数 y=ax 公在 R 上是增函数,故 a>1.
(3) a > a ;
-
(4) a-0.5 <a -0.6.
解 ∵ -<,且 a < a ,
∴ 函数 y=ax 公在 R 上是减函数,故 0<a<1.
-
解 ∵ -0.5>-0.6,且 a-0.5< a-0.6 ,
∴ 函数 y=ax 公在 R 上是减函数,故 0<a<1.
6. 分别求满下列条件的实数 x 的取值范围:
(1) 2x > 8;
解 ∵ 2x>8,即2x>23,
∴ x>3,
∴满足 2x>8 的实数 x 的取值范围是(3,+∞).
(2) 3x < ;
解 ∵ 3x < ,即3x < 3-3,
∴ x < -3,
∴满足 3x< 的实数 x 的取值范围是(-∞,-3).
(3) ()x>;
解 ∵ ()x > ,即 ()x>2 = () ,
∴ x < -,
∴满足 ()x> 的实数 x 的取值范围是(-∞,-).
(4) 5x < 0.2.
解 ∵ 5x<0.2,即 5x< = 5-1,
∴ x <-3,
∴满足 5x<0.2 的实数 x 的取值范围是(-∞ ,-1).
7. 函数 y=2-x 的图象为 ( ).
A
例 4
某种放射性物质不断变化为其他物质,每经过1年,这种物质剩留的质量是原来的 84%.写出这种物质的剩留量关于时间的函数关系式.
解 设该物质最初的质量是 1,经过年剩留量是y.
经过1年,剩留量 y=1×0.84=0.841;
经过 2年,剩留量 y=0.84×0.84=0842;
......
一般地,经过 x 年,剩留量 y=0.84x(x>0,x∈N*).
例 5
某种储蓄按复利计算利息,若本金为 a 元,每期利率为r,设存期是 x (x∈N*),本利和(本金加上利息)为 y 元.
(1)写出本利和 y 随存期 x 变化的函数关系式;
(2)已知存入本金 1000 元,每期利率为 2.25%,试计算 5 期后的本利和.
(1) 写出本利和 y 随存期 x 变化的函数关系式;
解 已知本金为a元,利率为r,则1期后的本利和为
y=a-ar =a(1+r),
2 期后的本利和为y=a(1+r) +a(1+r)r=a(1+r)2,
3 期后的本利和为y=a(1+r)3,......
x 期后的本利和为y=a(1+r)x,x∈N*,
即本利和y随存期x变化的函数关系式为
y=a(1+r)x,x∈N*.
(2) 已知存入本金 1000 元,每期利率为 2.25%,试计算 5 期后的本利和.
解 将 a=1000(元),r=2.25%,x=5 代入上式,
得 y =1000×(1+2.25%)5
= 1000×1.02255 ≈ 1117.68(元),
即5期后的本利和约为 1117.68 元.
思 考
在例 5 中,请借助计算器解答下列问题:
(1) 第几期后的本利和超过本金的1.5倍
(2) 要使 10 期后的本利和翻一番,利率应为多少 (精确到 0.001)
例 6
2000~2002 年,我国国内生产总值年平均增长7.8%. 按照这个增长速度,画出从 2000 年开始我国年国内生产总值随时间变化的图象,并通过图象观察到 2016 年我国年国内生产总值约为 2000 年的多少倍 (结果取整数).
解 设 2000 年我国年国内生产总值是 1,x 年后我国年国内生产总值为 y .
因为国内生产总值年平均增长 7.8%,
所以从 2001 年开始,每年的国内生产总值是上一年的 1.078 倍,
则经过1年,y=1×1.078 =1.078;
经过2年,y=1.078×1.078= 1.0782;
经过3年,y=1.0782×1.078=1.0783;······
一般地,经过x年,我国年国内生产总值y=1.078x,
x ∈N*.
画出指数函数 y=1.078x 的图象,如图 6-2-3 所示从图象上看出,当x=16 时,y≈3.
答 到2016 年我国国内生产总值约为 2000 年的3倍.
练 习
1. 已知 2016 年我国国内生产总值为a,设以后每年的年
平均增长率为 b,试写出 x 年后国内生产总值 y 和 x
之间的函数关系式:
解 因为2016年国内生产总值为a,以后每年的年平均增长率为b,
2017年为第一年,
则一年后,国内生产总值为:a +ab=a(1+b),
二年后,国内生产总值为:
a(1+)+a(1+b)b=a(1+b)2,
三年后,国内生产总值为:
a(1+b)2+a(1+b)2b=a(1+b)3,
······
则x年后,国内生产总值:
y=a(1+b)x (x∈N*)
2. 某种产品的年销售量为 10 000 件,由于其他新产品的
出现,估计该产品的市场需求每年下降 10%. 写出x年
后,年销售量 y (单位:件) 和 x (单位:年) 之间的函
数关系式.
解 1年后销售量为: a-a·15% =a(1-15%);
2年后销售量为:
a(1-15%) -a(1-15%)·15%=a(1-15%)2;
3年后销售量为:
a(1-15%)2-a(1-15%)2·15%=a(1-15%)3;
······
x年后销售量为:y=a(1-15%)x =a·0.85x(x∈N*).
3. 某人向银行贷款 10 万元做生意,约定按利率 7% 的复
利计算利息,写出x年后,需要还款总数 y (单位:万
元) 和 x (单位:年) 之间的函数关系式,并用计算器计
算 5 年后的还款总额.
解 由题意可得,
一年后还款总额为:10+10×7%=10× (1+7%),
二年后还款总额为:
10× (1+7%)+10× (1+7%) ×7%=10× (1+7%)2,
三年后还款总额为:
10×(1+7%)2+10×(1+7%)2×7%=10×(1+7%)3,
······
又因为x年后,需要还款总额为y,
所以 y=10×(1+7%) =10×1.07x( x∈N*).
当x=5时,y=10×1.075≈14.03.
即5年后的还款总额约为14.03万元
习题 6.2
感受·理解
1. 某种细胞分裂时,由 1个分裂成 2 个,2个分裂成 4 个
·····依此类推,写出这样的一个细胞分裂 x 次后,得
到的细胞个数 y 与分裂次数 之间的函数关系式.
解 由题意知该函数模型为指数函数,
设 y=ax (a>0,a≠1);
∴当x=1时,y=2,
∴ a=2,∴y=2x(x∈N*).
2. 用清水漂洗衣服,每次能洗去污垢的. 设洗前衣服上
的污垢量为 1,写出衣服上存留的污垢量 y 与漂洗次
数 x 之间的函数关系式. 若要使存留的污垢不超过原
有的 1%,至少要漂洗几次
解 由条件知,每次存留的污垢是上一次存留污垢的,
故存留污垢 y 与漂洗次数 a 的函数关系式为:
y=()x (x∈N*).
若 y≤1%,则 ()x≤1%,
由()3 >1%,且()4<1%知,x≥4.
故至少要漂洗4次.
3. 比较下列各组数中两个数的大小:
(1) 1.7m,1.7m+l;
解 1.7m,1.7m+1可看作函数 y=1.7x 的两个函数值,
由于1.7>1,所以函数 y=1.7x 在R上单调递增,
由于m<m+1,所以1.7m<1.7m+1.
(2) 0.8-0.1,0.8-0.2;
解 0.8-0.1,0.8-0.2可看作函数 y=0.8x 的两个数值,
由于0.8<1,所以函数 y=0.8x在R上单调递减,
由于-0.1>-0.2,所以0.8-0.1<0.8-0.2.
(3) 0.9m,0.9m-1;
解 0.9m,0.9m-1 可看作函数 y=0.9x 的两个函数值,
由于0.9<1,所以函数 y=0.9x 在R上单调递减,
由于m>m-1,所以 0.9m<0.9m-1.
(4) 0.6181.9,0.6181.8.
解 0.6181.9,0.6181.8可看作函数 y=0.618x 的两个数值,
由于0.618<1,所以函数 y=0.618x在R上单调递减,
由于1.9>1.8,所以0.6181.9 < 0.6181.8.
4. 分别把下列各题中的 3 个数按从小到大的顺序用不等
号连接起来:
(1) 22.1,21.9,0.32.1;
解 22.1>1,21.9>1,0.32.1<1,
又 y=2x 在 R 上单调递增,
2.1>1.9,22.1>21.9,
因此 0.32.1<21.9<22.1.
(2) 22.5,2.50,()2.5;
(3) 0.80.8,0.80.9,1.20.8;
解 22.5>1,2.50=1,()2.5<1,因此 22.5<2.50<()2.5.
解 0.80.8<1,0.80.9<1,1.20.8>1,
又y=0.8x在R上单调递减,0.8<0.9,则0.80.9<0.80.8,
因此 0.80.9 <0.80.8 <1.20.8.
(4) () ,() ,() .
-
-
-
解 () =() >1, () =() <1, () >1,
又y=()x在R上单调递增, < ,则() < () ,
因此 () <() <() .
-
-
-
-
5. 设 m,n 为实数,已知下列不等式成立,试比较 m,n
的大小:
(1) 2m < 2n;
解 ∵ 2>1.
∴ y=2x 在R上是单调增函数,
∵ 2m<2n.
∴m<n;
(2) 0.2m < 0.2n;
解 ∵0<0.2<1,
∴y=0.2x 在R上是单调减函数,
又∵0.2m<0.2n.
∴m>n;
(3) am<an (0<a<1).
解 ∵0<a<1.
∴y=ax 在R上是单调减函数,
又∵ am<an
∴m>n.
6. 设 a 为实数,a>0,a≠1.已知下列不等式成立,求 a
的取值范围:
(1) a3< a2;
解:∵ a3<a2,
∴函数y=ax 在 R 上是减函数,∴0<a<1.
(2) a0.8< a0.5;
解:∵ a0.8<a0.5,
∴函数y=ax 在 R 上是减函数,∴0<a<1.
(3) a-2 > a-3;
解:∵ a-2>a-3,
∴函数y=ax 在 R 上是增函数,∴a>1.
(4) am > an (m>n).
解:∵ am>an,
∴函数y=ax 在 R 上是增函数,∴a>1.
7. 解下列方程:
(1) 2x=;
解 由2x=,可得2x=2 ,
由指数函数是单调函数可得 x=.
综上所述,结论是:方程 2x= 的解是 x=.
(2) 4x=8;
解 由4x=8,可得(22) x=23,即 22x=23,
由指数函数是单调函数可得 2x=3.
解得 x=.
(3) 2x=3x.
解 由2x=3x,可得 =1,即()x=1,
即 ()x = ()0 ,
由指数函数是单调函数可得 x=0.
8. 求满足下列条件的实数 x 的取值范围:
(1) 3x< 9;
(2) 2x > ;
解 由3x<9,得3x<32. ∴x<2;
解 由2x>,得 2x>2-3. ∴x>-3;
(3) ()x >;
(4) 3x >7x .
解 由()x >,得3-x>3 . ∴ -x> 则 x<-;
解 由3x>7x,根据幂函数的性质,可得 x<0.
9. 设 f(x)=3x,求证:
(1) f(x)f(y) = f(x+y);
解 ∵ f(x) =3x.
∴左边=3x·3y=3x+y,右边=3x+y,
即左边=右边,
∴原式得证.
(2) f(x)÷f(y) = f(x-y).
解 ∵ f(x)=3x,
∴左边==3x-y,右边= 3x-y,
即左边=右边,
∴ 原式得证.
10. (1) 一电子元件厂去年生产某种规格的电子元件 a 个,
计划从今年开始的m年内,每年生产此种规格电子
元件的产量比上一年增长 p%,试写出此种规格电子
元件的年产量随年数变化的函数关系式;
解 设从今年开始的第x年的电子元件的产量为y,去年电子元件的产量为a个,今年是第一年,
第一年电子元件的产量为:a+ap% = a(1+p%);
第二年电子元件的产量为:
a(1+p%)+a(1+p%)p% = a(1+p%)2
第三年电子元件的产量为:
a(1+p%)2+a(1+p%)p%=a(1+p%)3
······
所以 y=a(1+p%)x (0<x<m,x∈N);
(2) 一电子元件厂去年生产某种规格电子元件的成本是 a
元/个,计划从今年开始的 m 年内,每年生产此种规
格电子元件的单件成本比上一年下降 p%,试写出此
种规格电子元件的单件成本随年数变化的函数关系式.
解 设从今年开始的第x年的电子元件的单件成本为y,
去年电子元件的成本是a元/个,今年是第一年,
第一年电子元件的单件成本为:a-ap%=a(1-p%).0
第二年电子元件的单件成本为:
a(1-p%)-a(1-p%)p% = a(1-p%)2
第三年电子元件的单件成本为:
a(1-p%)2-a(1-p%)p% = a(1-p%)3
所以 y=a(1-p%)x (0<x≤m,x∈N)
11. 设 a,k 为实数,a>0,a≠1. 试根据如图所示的函数
y=ka-x的图象,求 k 和 a 的值.
解 函数 y=ka-x 的图象过点(0,8)和点(3,1),
代入得 ,解得 .
8=ka0
1=ka-3
k=8
a=2
12. 设 a,b 为实数,a>0,a≠1. 已知函数 y=ax+b的图
象如图所示,求 a,b 的取值范围.
解 ∵函数 y=ax+b 在R上单调递增,
∴a>1.
∴ a的取值范围是(1,+∞);
∵当x=0时,y=a0+b=1+b<0.
∴b<-1,
∴b的取值范围是(-∞,-1)
∴a的取值范围是(1,+∞);b的取值范围是(-∞,-1).
思考·运用
13. 设 a 为实数,已知函数 f(x)=a+ (x∈R)是奇数,
求 a 的值.
解 由题意函数 f(x)的定义域为R,
所以 f(0)=a+= a+=0,解得a=- ,
经检验,当a=-时, f(x)=-+是奇函数,
故a的值为-.
14. 已知函数 f(x)= ,试讨论函数 f(x) 的单调性.
解 ∵ f(x)=1-,设x1,x2∈R,x1<x2,得2x1 <2x2,
f(x1)-f(x2)= -= ,
∴f(x1)<f(x2),
故函数 f(x) 是增函数.
15. 已知 y=f(x) 是定义在 R 上的奇函数,当 x<0 时,
f(x)=1+2x,你能画出此函数的图象吗
解 先在坐标系中画出函数 y=2x的图像,再向上平移1个单位,取 y 轴左侧部分再作出关于原点的对称图形,所得图像就是函数 y=f(x) 的图像(包括原点),如图所示.
16. 有些家用电器(如冰箱等)使用了氟化物,氟化物的释
放破坏了大气上层的臭氧层,使臭氧含量 Q 呈指数
函数型变化,在氟化物排放量维持某种水平时,具
有关系式Q=Q0e-0.0025t,其中Q0是臭氧的初始量.
(1) 随时间 t 的增加,臭氧的含量是增加还是减少
(2) 试估计多少年以后将会有一半的臭氧消失.
(用计算器计算)
(1) 随时间 t 的增加,臭氧的含量是增加还是减少
解 对于函数Q=Q0e-0.0025t1,显然 Q>0,
任取 t1>t2,则 t2-t1<0,
则 = =e-0.0025(t1-t2) =e0.0025(t2-t1),
∵ t2- t1<0,∴ =e0.0025(t2-t1) <e0 =1,∴Q1<Q2,
因此随着时间t的增加,臭氧的含量是减少的.
(2) 试估计多少年以后将会有一半的臭氧消失.
(用计算器计算)
解:令=e-0.0025t=,
解得-0.0025t=ln≈-0.6931,
从而 t≈277.
∴估计277年以后将会有一半臭氧消失.
探究·拓展
17. 已知函数 f(x)=2x,对于任意的 x1,x2∈R,试比较
与f()的大小关系.
解 ∵ f(x)=2x,
∴ = ,f() =2 ,
则 -f() = -2
≥ -2 =2 -2 =0.
当且仅当2x1=2x2 时等号成立,即 x1=x2 时等号成立.
当 x1=x2时, = f();
当 x1≠x2时, > f().
本课结束
This lesson is over
THANKS!
第6章
幂函数指数函数和对数函数
6 . 2
指数函数
试考察下列问题:
(1) 在 4.1节研究细胞分裂时,得到函数 y=2x.
(2) 在4.2.2节的例10 中,得到函数y=0.999 879x.
(3) 庄子曰:“一尺之捶,日取其半,万世不竭” (“捶”同“棰”). 设经过的天数为 x (天),木棰剩余的长度为 y (尺),则有 y=()x.
●函数 y=2x,y=0.999 879x,y=()x具有什么共同特征
这些函数的表达式都是指数幂形式,底数为常数,指数为自变量,这样的函数称为指数函数.
庄子,战国中期著名的思想家、哲学家和文学家,是道家学派的主要代表人物之一,主要著作有《庄子》.
一、指数函数
一般地,
函数
y=ax (a>0,a≠1)
叫作指数函数(exponential function),它的定义域是 R .
【思考】
当指数函数的底数 a=0,a=1,a<0时,对自变量 x的取值有何影响
提示:(1) 如果a=0,当x>0时,ax恒等于0,没有研究的必要;当x≤0时,ax无意义.
(2) 如果a<0,例如y=(-4)x,这时对于x=,,该函数无意义.
(3) 如果 a=1,则 y=1x 是一个常量,没有研究的价值.
为了避免上述各种情况,所以规定 a>0,且a≠1.
在图6-2-1中,我们同时画出了指数函数 y=10x,y=2x和 y=()x 的图象. 观察图6-2-1,通过研究函数的定义域、值域、奇偶性、单调性等,我们可以发现指数函数的性质如表 6-2-1 所示.
二、指数函数 y=ax(a>0,a≠1)的图象与性质
a>1 0<a<1
图象
a>1 0<a<1
性质 (1) 定义域:________
(2) 值域: ______________
(3) 图象过定点_________,图象在 x 轴上方
(4)在(-∞,+∞) 上是增函数; 当x>0时,y>1; 当x<0时,0<y<1. 在(-∞,+∞)上是减函数;
当x>0时,0<y<1;
当x<0时,y>1.
R
(0,+∞)
(0,1)
注意:
在同一坐标系中有多个指数函数图象时,图象的相对位置与底数的大小有如下关系:
① 在y轴右侧,图象从上到下相应的底数由大变小:
② 在y轴左侧,图象从下到上相应的底数由大变小,即无论在y轴的左侧还是右侧,底数按逆时针方向变大.这一性质可通过令x=1时,y的取值去理解.
探 究
(1) 在画图过程中,你还发现了指数函数的其他性质吗
(2) 函数 y=2x与 y=()x的图象有怎样的关系 你能得到更般的结论吗
例 1
比较下列各组数中两个数的大小:
(1) 1.52.5,1.53.2;
解:考察指数函数 y=1.5x.
因为 1.5>1,
所以 y=1.5x在 R 上是增函数.
又因为2.5<3.2,所以 1.52.5<1.53.2.
(2) 0.5-1.2,0.5-1.5;
解:考察指数函数 y=0.5x.
因为 0<0.5<1,
所以 y=0.5x在 R 上是减函数.
又因为 -1.2>-1.5,
所以 0.5-1.2<0.5-1.5.
(3) 1.50.3 ,0.81.2.
解:考察指数函数 y=1.5x.
因为 1.5>1,
所以 y=1.5x在 R 上是增函数.
又因为0.3>0,所以 1.50.3>1.50>1.
同理 0.81.2<0.80=1,
故 1.50.3 > 0.81.2.
例 2
(1) 已知 3x≥30.5,求实数 的取值范围;
解:因为 3 > 1.
所以 指数函数 y=3x 在 R 上是增函数,
由 3x≥30.5 可得 x≥0.5.
故的取值范围为区间 [0.5,+∞).
(2) 已知 0.2x<25,求实数 x的取值范围.
解 因为 0<0.2x<1,
所以指数函数 y=0.2x 在 R 上是减函数,
因为 25 =()-2 = 0.2-2,
所以 0.2x < 0.2-2.
由此可得 x>-2.
故 x 的取值范围为区间(-2,+∞).
例 3
(1) y=2x-2; (2) y=2x+2.
说明下列函数的图象与指数函数 y=2x 的图象的关系并画出它们的示意图:
解 比较函数 y=2x与函数 y=2x-2,y=2x+2的取值关系,
列表如表 6-2-2 所示.
一般地,因为函数 y=2x-2中x=a+2对应的y值与函数 y=2x 中 x=a 对应的 y 值相等,所以将指数函数y=2x 的图象向平移2个单位长度,就得到函数 y=2x-2 的图象.
同样地,因为函数 y=2x+2 中 x=a-2 对应的y值与函数 y=2x 中 x=a 对应的 y 值相等,所以将指数函数y=2x的图象向左平移2个单位长度,就得到函数y=2x+2的图象.
这些函数的图象如图 6-2-2 所示.
思 考
函数 y=ax+h与函数 y=ax (a>0,a≠1,h≠0) 的图象之间有怎样的关系
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) y=x6 是指数函数. ( )
(2) 指数函数的图象都在x轴的上方. ( )
(3) 若指数函数 y=ax 是减函数,则0<a<1. ( )
2. 若函数 f(x)=(a2-3a+3)ax是指数函数,则 ( )
A. a=1或a=2 B. a=1
C. a=2 D. a>0且a≠1
C
解析
a2-3a+3=1,
解析:由指数函数的定义得 解得a=2.
a>0且a≠1,
3. 已知函数 f(x)=3x-()x,则 f(x) ( )
A. 是奇函数,且在R上是增函数
B. 是偶函数,且在R上是增函数
C. 是奇函数,且在R上是减函数
D. 是偶函数,且在R上是减函数
A
4. 函数 y=的定义域是 ( )
A. (-∞,0) B. (-∞,0]
C. [0,+∞) D. (0,+∞)
C
解析:由2x-1≥0得2x≥1,即 x≥0,
所以函数的定义域为[0,+∞).
解析
解析:由已知得 解得
所以 f(x) = ()x+3,
所以 f(-2) =()-2+3=4+3=7.
a=,
b=3,
a-1 +b=5,
a0+b=4,
5. 已知函数 f(x)=ax+b(a>0,且a≠1)经过点(-1,5),
(0,4),则 f(-2)的值为__________.
7
解析
【跟踪训练】
1. 函数 y=(a-2)2ax 是指数函数,则 ( )
A. a=1或a=3 B. a=1
C. a=3 D. a>0且a≠1
C
解析
(a-2)2=1,
解析:由指数函数定义知 解得 a=3.
a>0,且a≠1
2. 当x>0时,指数函数(a-1)x<1 恒成立,则实数 a 的
取值范围是 ( )
A. (2,+∞) B. (1,2)
C. (1,+∞) D. R
B
解析:因为当 x>0 时,(a-1)x<1恒成立,
所以0<a-1<1,即1<a<2.
解析
3. 函数 f(x) =()x 在区间 [-2,2] 上的最小值是 ( )
A. B. - C. 4 D. -4
A
解析:函数 f(x)=()x 在定义域R上单调递减,
所以 f(x) 在区间[-2,2]上的最小值是f(2)=()2= .
解析
4. 已知 a=30.2,b=0.2-3,c=(-3)0.2,则 a,b,c 的大
小关系为 ( )
A. a>b>c B. b>a>c
C. c>a>b D. b>c>a
B
解析:c <0,b=53>3,1<a<3,所以 b>a>c.
解析
5. 已知函数 f(x)=ax(a>0,且a≠1)的图象经过点(2,4),
则a=________,若 a2x+1<a3x-1,则x的取值范围是
____________.
2
x>2
解析:因为 f(x) 的图象经过点(2,4),
所以 a2=4,解得a=2,
若a2x+1<a3x-1,即22x+1<23x-1,
故 2x+1<3x-1,解得x>2.
解析
练 习
1. 下列各数中,哪些大于 1,哪些小于 1
() , () , () ,(0.16)0.2.
-
-
() > ()0=1;
() > ()0=1;
-
() < ()0=1;
-
(0.16)0.2 < (0.16)0=1.
2. 指出下列函数的单调性:
(1) y=5x;
解 ∵ y=5x ,x∈R,
∴根据指数函数的性质,5 > 1,
则函数在R上单调递增.
(2) y=()x;
解 ∵ y=()x ,x∈R,
∴根据指数函数的性质, 0<<1,
则函数在R上单调递增.
(3) y=0.5x;
解 ∵ y=0.5x,x∈R.
∴ 根据指数函数的性质0<0.5<1,
则函数在R上单调递减.
(4) y=-2x.
解 ∵ y=-2x,x∈R.
∴ y′=-2xln2<0 在 R 上恒成立.
则函数在 R 上单调递减.
3. 设 a 为实数如果指数函数 f(x)=(a-1)x是 R 上的减函
数,那么 a 的取值范围是( ).
A. a<2 B. a>2
C. 1<a<2 D. 0<a<1
C
4. 比较下列各组数中两个值的大小关系:
(1) 3.10.5 ,3.12.3 ;
(2) ()-1.5, ()-1.8;
解 ∵ y=3.1x 在 R 上单调递增,0.5<2.3,
∴ 3.10.5<3.12.3.
解 ∵ y=()x 在 R 上单调递增, -1.5>-1.8,
∴ ()-1.5> ()-1.8 .
(4) ()-0.3, ()-0.24;
(3) 0.62,0.63;
解 ∵ y=0.6x 在 R 上单调递减,2<3,
∴ 0.62 < 0.6 3.
解 ∵ y=()x 在 R 上单调递增, -0.3<-0.24,
∴ ()-0.3> ()-0.24 .
(5) 0.53.2,1.32.1;
(6) 2.3-2.5,0.2-0.1.
解 ∵ 0.53.2< 0.50=1,1.32.1>1.30=1,
∴ 0.53.2 < 1.32.1.
解 ∵ 2.3-2.5< 2.30=1,0.2-0.1>0.20=1,
∴ 2.3-2.5 < 0.2-0.1.
5. 分别根据下列条件确定正数 a 与 1 的大小关系:
(1) a < a ;
解 ∵ <,且 a < a ,
∴ 函数 y=ax 公在 R 上是增函数,故 a>1.
(2) a > a ;
解 ∵ >,且 a > a ,
∴ 函数 y=ax 公在 R 上是增函数,故 a>1.
(3) a > a ;
-
(4) a-0.5 <a -0.6.
解 ∵ -<,且 a < a ,
∴ 函数 y=ax 公在 R 上是减函数,故 0<a<1.
-
解 ∵ -0.5>-0.6,且 a-0.5< a-0.6 ,
∴ 函数 y=ax 公在 R 上是减函数,故 0<a<1.
6. 分别求满下列条件的实数 x 的取值范围:
(1) 2x > 8;
解 ∵ 2x>8,即2x>23,
∴ x>3,
∴满足 2x>8 的实数 x 的取值范围是(3,+∞).
(2) 3x < ;
解 ∵ 3x < ,即3x < 3-3,
∴ x < -3,
∴满足 3x< 的实数 x 的取值范围是(-∞,-3).
(3) ()x>;
解 ∵ ()x > ,即 ()x>2 = () ,
∴ x < -,
∴满足 ()x> 的实数 x 的取值范围是(-∞,-).
(4) 5x < 0.2.
解 ∵ 5x<0.2,即 5x< = 5-1,
∴ x <-3,
∴满足 5x<0.2 的实数 x 的取值范围是(-∞ ,-1).
7. 函数 y=2-x 的图象为 ( ).
A
例 4
某种放射性物质不断变化为其他物质,每经过1年,这种物质剩留的质量是原来的 84%.写出这种物质的剩留量关于时间的函数关系式.
解 设该物质最初的质量是 1,经过年剩留量是y.
经过1年,剩留量 y=1×0.84=0.841;
经过 2年,剩留量 y=0.84×0.84=0842;
......
一般地,经过 x 年,剩留量 y=0.84x(x>0,x∈N*).
例 5
某种储蓄按复利计算利息,若本金为 a 元,每期利率为r,设存期是 x (x∈N*),本利和(本金加上利息)为 y 元.
(1)写出本利和 y 随存期 x 变化的函数关系式;
(2)已知存入本金 1000 元,每期利率为 2.25%,试计算 5 期后的本利和.
(1) 写出本利和 y 随存期 x 变化的函数关系式;
解 已知本金为a元,利率为r,则1期后的本利和为
y=a-ar =a(1+r),
2 期后的本利和为y=a(1+r) +a(1+r)r=a(1+r)2,
3 期后的本利和为y=a(1+r)3,......
x 期后的本利和为y=a(1+r)x,x∈N*,
即本利和y随存期x变化的函数关系式为
y=a(1+r)x,x∈N*.
(2) 已知存入本金 1000 元,每期利率为 2.25%,试计算 5 期后的本利和.
解 将 a=1000(元),r=2.25%,x=5 代入上式,
得 y =1000×(1+2.25%)5
= 1000×1.02255 ≈ 1117.68(元),
即5期后的本利和约为 1117.68 元.
思 考
在例 5 中,请借助计算器解答下列问题:
(1) 第几期后的本利和超过本金的1.5倍
(2) 要使 10 期后的本利和翻一番,利率应为多少 (精确到 0.001)
例 6
2000~2002 年,我国国内生产总值年平均增长7.8%. 按照这个增长速度,画出从 2000 年开始我国年国内生产总值随时间变化的图象,并通过图象观察到 2016 年我国年国内生产总值约为 2000 年的多少倍 (结果取整数).
解 设 2000 年我国年国内生产总值是 1,x 年后我国年国内生产总值为 y .
因为国内生产总值年平均增长 7.8%,
所以从 2001 年开始,每年的国内生产总值是上一年的 1.078 倍,
则经过1年,y=1×1.078 =1.078;
经过2年,y=1.078×1.078= 1.0782;
经过3年,y=1.0782×1.078=1.0783;······
一般地,经过x年,我国年国内生产总值y=1.078x,
x ∈N*.
画出指数函数 y=1.078x 的图象,如图 6-2-3 所示从图象上看出,当x=16 时,y≈3.
答 到2016 年我国国内生产总值约为 2000 年的3倍.
练 习
1. 已知 2016 年我国国内生产总值为a,设以后每年的年
平均增长率为 b,试写出 x 年后国内生产总值 y 和 x
之间的函数关系式:
解 因为2016年国内生产总值为a,以后每年的年平均增长率为b,
2017年为第一年,
则一年后,国内生产总值为:a +ab=a(1+b),
二年后,国内生产总值为:
a(1+)+a(1+b)b=a(1+b)2,
三年后,国内生产总值为:
a(1+b)2+a(1+b)2b=a(1+b)3,
······
则x年后,国内生产总值:
y=a(1+b)x (x∈N*)
2. 某种产品的年销售量为 10 000 件,由于其他新产品的
出现,估计该产品的市场需求每年下降 10%. 写出x年
后,年销售量 y (单位:件) 和 x (单位:年) 之间的函
数关系式.
解 1年后销售量为: a-a·15% =a(1-15%);
2年后销售量为:
a(1-15%) -a(1-15%)·15%=a(1-15%)2;
3年后销售量为:
a(1-15%)2-a(1-15%)2·15%=a(1-15%)3;
······
x年后销售量为:y=a(1-15%)x =a·0.85x(x∈N*).
3. 某人向银行贷款 10 万元做生意,约定按利率 7% 的复
利计算利息,写出x年后,需要还款总数 y (单位:万
元) 和 x (单位:年) 之间的函数关系式,并用计算器计
算 5 年后的还款总额.
解 由题意可得,
一年后还款总额为:10+10×7%=10× (1+7%),
二年后还款总额为:
10× (1+7%)+10× (1+7%) ×7%=10× (1+7%)2,
三年后还款总额为:
10×(1+7%)2+10×(1+7%)2×7%=10×(1+7%)3,
······
又因为x年后,需要还款总额为y,
所以 y=10×(1+7%) =10×1.07x( x∈N*).
当x=5时,y=10×1.075≈14.03.
即5年后的还款总额约为14.03万元
习题 6.2
感受·理解
1. 某种细胞分裂时,由 1个分裂成 2 个,2个分裂成 4 个
·····依此类推,写出这样的一个细胞分裂 x 次后,得
到的细胞个数 y 与分裂次数 之间的函数关系式.
解 由题意知该函数模型为指数函数,
设 y=ax (a>0,a≠1);
∴当x=1时,y=2,
∴ a=2,∴y=2x(x∈N*).
2. 用清水漂洗衣服,每次能洗去污垢的. 设洗前衣服上
的污垢量为 1,写出衣服上存留的污垢量 y 与漂洗次
数 x 之间的函数关系式. 若要使存留的污垢不超过原
有的 1%,至少要漂洗几次
解 由条件知,每次存留的污垢是上一次存留污垢的,
故存留污垢 y 与漂洗次数 a 的函数关系式为:
y=()x (x∈N*).
若 y≤1%,则 ()x≤1%,
由()3 >1%,且()4<1%知,x≥4.
故至少要漂洗4次.
3. 比较下列各组数中两个数的大小:
(1) 1.7m,1.7m+l;
解 1.7m,1.7m+1可看作函数 y=1.7x 的两个函数值,
由于1.7>1,所以函数 y=1.7x 在R上单调递增,
由于m<m+1,所以1.7m<1.7m+1.
(2) 0.8-0.1,0.8-0.2;
解 0.8-0.1,0.8-0.2可看作函数 y=0.8x 的两个数值,
由于0.8<1,所以函数 y=0.8x在R上单调递减,
由于-0.1>-0.2,所以0.8-0.1<0.8-0.2.
(3) 0.9m,0.9m-1;
解 0.9m,0.9m-1 可看作函数 y=0.9x 的两个函数值,
由于0.9<1,所以函数 y=0.9x 在R上单调递减,
由于m>m-1,所以 0.9m<0.9m-1.
(4) 0.6181.9,0.6181.8.
解 0.6181.9,0.6181.8可看作函数 y=0.618x 的两个数值,
由于0.618<1,所以函数 y=0.618x在R上单调递减,
由于1.9>1.8,所以0.6181.9 < 0.6181.8.
4. 分别把下列各题中的 3 个数按从小到大的顺序用不等
号连接起来:
(1) 22.1,21.9,0.32.1;
解 22.1>1,21.9>1,0.32.1<1,
又 y=2x 在 R 上单调递增,
2.1>1.9,22.1>21.9,
因此 0.32.1<21.9<22.1.
(2) 22.5,2.50,()2.5;
(3) 0.80.8,0.80.9,1.20.8;
解 22.5>1,2.50=1,()2.5<1,因此 22.5<2.50<()2.5.
解 0.80.8<1,0.80.9<1,1.20.8>1,
又y=0.8x在R上单调递减,0.8<0.9,则0.80.9<0.80.8,
因此 0.80.9 <0.80.8 <1.20.8.
(4) () ,() ,() .
-
-
-
解 () =() >1, () =() <1, () >1,
又y=()x在R上单调递增, < ,则() < () ,
因此 () <() <() .
-
-
-
-
5. 设 m,n 为实数,已知下列不等式成立,试比较 m,n
的大小:
(1) 2m < 2n;
解 ∵ 2>1.
∴ y=2x 在R上是单调增函数,
∵ 2m<2n.
∴m<n;
(2) 0.2m < 0.2n;
解 ∵0<0.2<1,
∴y=0.2x 在R上是单调减函数,
又∵0.2m<0.2n.
∴m>n;
(3) am<an (0<a<1).
解 ∵0<a<1.
∴y=ax 在R上是单调减函数,
又∵ am<an
∴m>n.
6. 设 a 为实数,a>0,a≠1.已知下列不等式成立,求 a
的取值范围:
(1) a3< a2;
解:∵ a3<a2,
∴函数y=ax 在 R 上是减函数,∴0<a<1.
(2) a0.8< a0.5;
解:∵ a0.8<a0.5,
∴函数y=ax 在 R 上是减函数,∴0<a<1.
(3) a-2 > a-3;
解:∵ a-2>a-3,
∴函数y=ax 在 R 上是增函数,∴a>1.
(4) am > an (m>n).
解:∵ am>an,
∴函数y=ax 在 R 上是增函数,∴a>1.
7. 解下列方程:
(1) 2x=;
解 由2x=,可得2x=2 ,
由指数函数是单调函数可得 x=.
综上所述,结论是:方程 2x= 的解是 x=.
(2) 4x=8;
解 由4x=8,可得(22) x=23,即 22x=23,
由指数函数是单调函数可得 2x=3.
解得 x=.
(3) 2x=3x.
解 由2x=3x,可得 =1,即()x=1,
即 ()x = ()0 ,
由指数函数是单调函数可得 x=0.
8. 求满足下列条件的实数 x 的取值范围:
(1) 3x< 9;
(2) 2x > ;
解 由3x<9,得3x<32. ∴x<2;
解 由2x>,得 2x>2-3. ∴x>-3;
(3) ()x >;
(4) 3x >7x .
解 由()x >,得3-x>3 . ∴ -x> 则 x<-;
解 由3x>7x,根据幂函数的性质,可得 x<0.
9. 设 f(x)=3x,求证:
(1) f(x)f(y) = f(x+y);
解 ∵ f(x) =3x.
∴左边=3x·3y=3x+y,右边=3x+y,
即左边=右边,
∴原式得证.
(2) f(x)÷f(y) = f(x-y).
解 ∵ f(x)=3x,
∴左边==3x-y,右边= 3x-y,
即左边=右边,
∴ 原式得证.
10. (1) 一电子元件厂去年生产某种规格的电子元件 a 个,
计划从今年开始的m年内,每年生产此种规格电子
元件的产量比上一年增长 p%,试写出此种规格电子
元件的年产量随年数变化的函数关系式;
解 设从今年开始的第x年的电子元件的产量为y,去年电子元件的产量为a个,今年是第一年,
第一年电子元件的产量为:a+ap% = a(1+p%);
第二年电子元件的产量为:
a(1+p%)+a(1+p%)p% = a(1+p%)2
第三年电子元件的产量为:
a(1+p%)2+a(1+p%)p%=a(1+p%)3
······
所以 y=a(1+p%)x (0<x<m,x∈N);
(2) 一电子元件厂去年生产某种规格电子元件的成本是 a
元/个,计划从今年开始的 m 年内,每年生产此种规
格电子元件的单件成本比上一年下降 p%,试写出此
种规格电子元件的单件成本随年数变化的函数关系式.
解 设从今年开始的第x年的电子元件的单件成本为y,
去年电子元件的成本是a元/个,今年是第一年,
第一年电子元件的单件成本为:a-ap%=a(1-p%).0
第二年电子元件的单件成本为:
a(1-p%)-a(1-p%)p% = a(1-p%)2
第三年电子元件的单件成本为:
a(1-p%)2-a(1-p%)p% = a(1-p%)3
所以 y=a(1-p%)x (0<x≤m,x∈N)
11. 设 a,k 为实数,a>0,a≠1. 试根据如图所示的函数
y=ka-x的图象,求 k 和 a 的值.
解 函数 y=ka-x 的图象过点(0,8)和点(3,1),
代入得 ,解得 .
8=ka0
1=ka-3
k=8
a=2
12. 设 a,b 为实数,a>0,a≠1. 已知函数 y=ax+b的图
象如图所示,求 a,b 的取值范围.
解 ∵函数 y=ax+b 在R上单调递增,
∴a>1.
∴ a的取值范围是(1,+∞);
∵当x=0时,y=a0+b=1+b<0.
∴b<-1,
∴b的取值范围是(-∞,-1)
∴a的取值范围是(1,+∞);b的取值范围是(-∞,-1).
思考·运用
13. 设 a 为实数,已知函数 f(x)=a+ (x∈R)是奇数,
求 a 的值.
解 由题意函数 f(x)的定义域为R,
所以 f(0)=a+= a+=0,解得a=- ,
经检验,当a=-时, f(x)=-+是奇函数,
故a的值为-.
14. 已知函数 f(x)= ,试讨论函数 f(x) 的单调性.
解 ∵ f(x)=1-,设x1,x2∈R,x1<x2,得2x1 <2x2,
f(x1)-f(x2)= -= ,
∴f(x1)<f(x2),
故函数 f(x) 是增函数.
15. 已知 y=f(x) 是定义在 R 上的奇函数,当 x<0 时,
f(x)=1+2x,你能画出此函数的图象吗
解 先在坐标系中画出函数 y=2x的图像,再向上平移1个单位,取 y 轴左侧部分再作出关于原点的对称图形,所得图像就是函数 y=f(x) 的图像(包括原点),如图所示.
16. 有些家用电器(如冰箱等)使用了氟化物,氟化物的释
放破坏了大气上层的臭氧层,使臭氧含量 Q 呈指数
函数型变化,在氟化物排放量维持某种水平时,具
有关系式Q=Q0e-0.0025t,其中Q0是臭氧的初始量.
(1) 随时间 t 的增加,臭氧的含量是增加还是减少
(2) 试估计多少年以后将会有一半的臭氧消失.
(用计算器计算)
(1) 随时间 t 的增加,臭氧的含量是增加还是减少
解 对于函数Q=Q0e-0.0025t1,显然 Q>0,
任取 t1>t2,则 t2-t1<0,
则 = =e-0.0025(t1-t2) =e0.0025(t2-t1),
∵ t2- t1<0,∴ =e0.0025(t2-t1) <e0 =1,∴Q1<Q2,
因此随着时间t的增加,臭氧的含量是减少的.
(2) 试估计多少年以后将会有一半的臭氧消失.
(用计算器计算)
解:令=e-0.0025t=,
解得-0.0025t=ln≈-0.6931,
从而 t≈277.
∴估计277年以后将会有一半臭氧消失.
探究·拓展
17. 已知函数 f(x)=2x,对于任意的 x1,x2∈R,试比较
与f()的大小关系.
解 ∵ f(x)=2x,
∴ = ,f() =2 ,
则 -f() = -2
≥ -2 =2 -2 =0.
当且仅当2x1=2x2 时等号成立,即 x1=x2 时等号成立.
当 x1=x2时, = f();
当 x1≠x2时, > f().
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
