6.3 对数函数 课件(共115张PPT)
文档属性
| 名称 | 6.3 对数函数 课件(共115张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 69.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 00:00:00 | ||
图片预览










文档简介
(共115张PPT)
第6章
幂函数指数函数和对数函数
6 . 3
对数函数
我们知道,在某细胞分裂过程中,细胞个数 y 是分裂次数 的指数函数 y=2x,因此,知道x的值 (输入值是分裂次数),就能求出y的值 (输出值是细胞个数). 现在,我们来研究相反的问题:知道了细胞个数 y,如何确定分裂次数x
为了求 y=2x 中的x,我们将 y=2x 改写成对数式为
x=log2y .
对于每一个给定的y值,都有唯一的值与之对应把y看作自变量, 就是 y 的函数. 这样就得到了一个新的函数.
前面提到的放射性物质,经过的时间 x (单位:年) 与物质剩留量 y 的关系式为
y=0.84x
改写成对数式为
x=log0.84y.
类似地,y 是自变量,x 是 y 的函数.
习惯上,仍用 x 表示自变量,用 y 表示它的函数. 这样,上面两个函数就分别写成 y=log2x 和 y=log0.84x.
类似还可以得到函数 y=log3x,y=log x 等.
● 函数 y=log2x,y=log0.84x,y=log3x,y=log x 具有
什么共同特征
这些函数的表达式都是对数的形式,底数是常数,真数是自变量,这样的函数称为对数函数.
一、对数函数
一般地,
函数
y=logax (a>0,a≠1)
叫作对数函数,它的定义域是(0,+∞).
提示:① a>0,且 a≠1;
② logax 的系数为1;
③自变量x的系数为1.
【思考】
对数函数解析式有什么特征
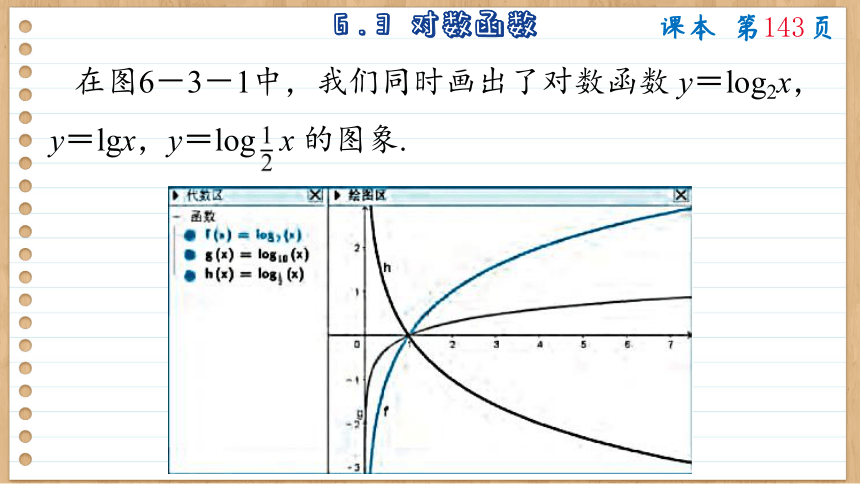
在图6-3-1中,我们同时画出了对数函数 y=log2x,y=lgx,y=log x 的图象.
观察图 6-3-1中的函数的图象,对照指数函数的性质,你发现对数函数 y=logax (a>0,a≠1) 有哪些性质
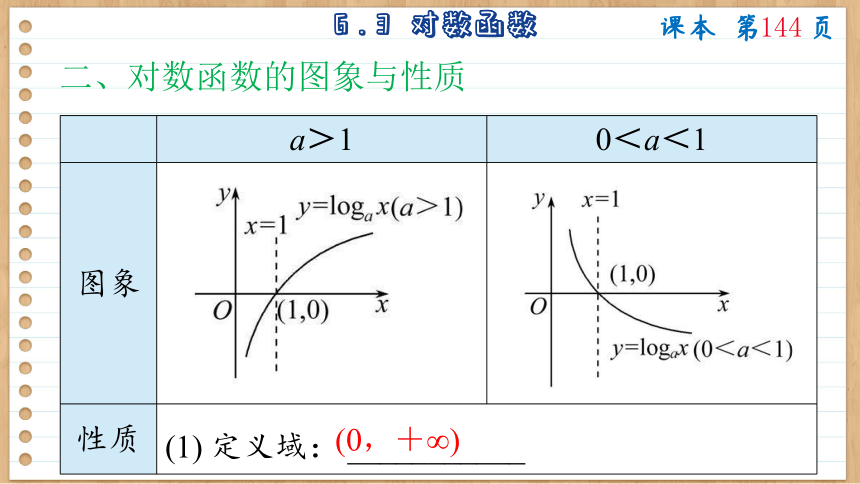
二、对数函数的图象与性质
a>1 0<a<1
图象
性质 (1) 定义域: ___________
(0,+∞)
a>1 0<a<1
性质 (2) 值域: R
(3) 图象过点(1,0)
(4) 在(0,+∞)上是增函数; 当0<x<1时,y<0; 当x>1时,y>0. 在(0,+∞)上是减函数;
当0<x<1时,y>0;
当x>1时,y<0.
【思考】
提示:当 x=1 时,loga1=0 恒成立,即对数函数的图象一定过点 (1,0) .
对于对数函数y=log2x,y=log3x,y=log x,y=log x,
···,为什么一定过点(1,0)
思 考
函数 y=logax 与函数 y=ax(a>0,a≠1)的定义域、值域之间有怎样的关系
画出下列两组函数的图象,并观察各组函数的图象,寻找它们之间的关系:
(1) y=2x,y=log2x;
(2) y=()x,y=log x.
由图可以看出,函数 y=2x与y=log2x 的图象关于直线 y=x 对称,函数 y=()x与 y=log x 的图象也关于直线 y=x 对称.
思 考
一般地,当a>0,a≠1时,函数 y=ax与 y=logax 的图象有怎样的关系
当 a>0,a≠1 时,y=logax 称为 y=ax 的反函数. 反之,y=ax 也称为 y=logax 的反函数.
一般地,如果函数 y=f(x) 存在反函数,那么它的反函数记作 y=f-1(x).
例 1
求下列函数的定义域:
(1) y=log0.2(4-x);
解: 当4-x>0,即x<4时,log0.2(4-x)有意义;
当 x≥4 时,log0.2(4-x)没有意义.
因此,函数 y=log0.2(4-x)的定义域是(-∞,4).
(2) y=loga (a>0,a≠1).
解:当>0,即 x>1时, loga有意义;
当 x≤1 时,loga 没有意义.
因此,函数 y=loga的定义域是(1,+∞).
例 2
比较下列各组数中两个数的大小:
(1) log23.4,log23.8;
解 考察对数函数 y=log2x.
因为 2>1,
所以 y=log2x 在区间(0,+∞)上是增函数.
又因为 0<3.4<3.8,
所以 log23.4<log23.8.
(2) log0.51.8,log0.52.1;
解 考察对数函数 y=log0.5x.
因为0<0.5<1,
所以 y=log0.5x 在区间(0,+∞)上是减函数.
又因为 0<1.8< 2.1,
所以 log0.51.8 > log0.52.1.
解 考察对数函数 y=log7x.
因为 7>1,
所以 y=log7x 在区间(0,+∞)上是增函数.
又因为 0<5<7,
所以 log75 < log77=1.
同理 log67 > log66=1,
所以 log75 < log67.
(3) 1og75,log67.
例 3
说明函数 y=log3(x+2) 与函数 y=log3x 的图的关系.
解 比较函数 y=log3(x+2)与 y =log3x 的取值关系,列表如表 6-3-2 所示.
一般地,函数 y=log3(x+2)中x=a-2 对应的 y 值与函数y=log3x中x=a对应的y值相等,则将对数函数 y=log3x 的图象向左平移2个单位长度,就得到函数y=log3(x+2) 的图象.
这两个函数的图象如图所示.
思 考
函数 y=log(x+b) 与函数 y=logax (a>0,a≠1,b≠0)的图象之间有怎样的关系
例 4
画出函数 y=log2∣x∣的图象,并根据图象写出函数的单调区间.
解:由于函数 y=f(x)=log2∣x∣满足对任意的 x∈(-8,0)∪(0,+∞) 都有
f(-x) = log2∣-x∣=log2∣x∣=f(x),
所以函数 y=log2∣x∣是偶函数,它的图象关于y轴对称.
当x>0时,log2∣x∣=lg2x. 因此,我们先画出函数 y=log2x (x>0)的图象C1,再作出 C1关于 y 轴对称的图象C2. C1和C2构成函数 y=log2∣x∣的图象,如图 6-3-4.
由图象可以知道,函数 y=log2∣x∣的减区间是(-∞ ,0),增区间是(0,+∞).
信息技术
在GGB中作出动态函数 y=ax与y=logax (a>0,a≠1)的图象,直观地理解第 145 页“思考”中的问题.
(1) 在输入框中输入“y=a∧x”,确认“创建滑动条:a”(图6-3-5)
(2) 在输入框中输入“y=log(a,x)”,敲回车确认;
(3) 拖动滑块a,观察两个图象的动态变化趋势 (图 6-3-6).
右击滑块 a 在“属性”中可设置参数 a 的范围及增量(每次变化的幅度).
练 习
1. 画出函数 y=log3x;与 y=log x 的图象,指出这两个函数图象之间的关系.
函数 y=log3x 在(0, +∞)上单调递增,且图象过点(1,0).
函数 y=log x 在(0,+∞)上单调递减,且图象过点(1,0).
log x=log3-1x=-log3x ,
两个函数的图象关于x轴对称
2. 求下列函数的定义域:
(1) y=log2(2x+1);
解 要使函数 y=log3(2x+1) 有意义,需满足2x+1>0,
解得 x>-,
故函数 y=log2(2x+1) 的定义域为(-,+∞);
(2) y=log0.5(2x-3)
解 要使函数y=log0.5(2x-3)有意义,需满足2x-3>0,
即 x>,
故函数 y=log0.5(2x-3)的定义域为(,+∞);
(3) y=log (2-x);
解 要使函数y=log (2-x) 有意义,
需满足2-x>0,
解得 x<2,
故函数 y= log (2-x)的定义域为(-∞ ,2);
(4) y=lg.
解 要使函数y=lg 有意义,需满足x-1>0,
解得 x>1,
故函数 y=lg 的定义域为(1,+∞);
3. 判断下列函数的单调性:
(1) y=log2x;
(2) y=log x;
解 ∵函数 y=log2x,x>0 的底数2>1,
∴该函数在 (0,+∞) 上单调递增;
解 ∵函数 y=log x,x>0 的底数0<<1,
∴该函数在 (0,+∞) 上单调递减;
(3) y=log7(2x+1);
解 ∵ 2x+1>0,∴x>-,
设 t=2x+1,则 y=log7t,t>-,
∵函数 t=2x+1 在(-,+∞)上单调递增,
且函数 y=log7t 在(0,+∞) 上单调递增,
∴由复合函数的单调性的“同增异减”性可得,
y=log7(2x+1)在(-,+∞)上单调递增;
(4) y=lg(3-2x).
解 ∵ 3-2x>0,∴x<,
设 t=3-2x,则 y=lgt,
∵函数 t=3-2x 在(-∞ ,)上单调递减,
且函数 y=lgt 在(0,+∞) 上单调递增,
∴由复合函数的单调性的“同增异减”性可得,
y=lg(3-2x)在(-∞ ,)上单调递减;
4. 比较下列各组数中两个数的大小:
(1) log35.4,log35.5;
(2) log π,log e;
解 ∵f(x)=log3x 在(0,+∞) 单调递增,且 5.4<5.5,
∴log35.4<log35.5;
解 ∵f(x)=log x 在(0,+∞) 单调递减,且 π>e,
∴log π<log e;
(3) lg 0.02,lg 3.12;
(4) ln 0.55,ln 0.56.
解 ∵f(x)=lgx 在(0,+∞) 单调递增,且 0.02<3.12,
∴lg0.02<lg3.12;
解 ∵f(x)=lnx 在(0,+∞) 单调递增,且 0.55<0.56,
∴ln0.55<ln0.56;
5. 解下列方程:
(1) log2(3x)=log2(2x+1);
解 ∵log2(3x)=log2(2a+1),
∴ 3x=2x+1,
即x=1.
(2) log5(2x+1) =log5(x2-2);
解 ∵ log5(2x+1)=log5(x2-2),
∴ 2x+1=x2-2,
∴ x=3 或 x=-1,
又∵真数都是大于0的,
当x=-1时,x2-2=-1<0.
∴x=-1舍去,即 x=3.
(3) lg = lg(x-1).
解 ∵lg = lg(x-1),
∴ = x-1 且x-1>0,
∴ x=2.
链 接
我们已经知道,函数 y=ax与y=logax (a>0,a≠1) 互为反函数. 一般地,设 A,B 分别为函数y=f(x)的定义域和值域,如果由函数y=f(x)可解得唯一 x=(y) 也是一个函数 (即对任意一个 y∈B,都有唯一的 x∈A 与之对应),那么就称函数 x=(y) 是函数 y=f(x) 的反函数,记作 x=f -1(y).
在 x=f-1(y)中,y 是自变量,x是y的函数. 习惯上改写成 y=f-1(x) (x∈B,y∈A) 的形式.
例如,求函数 y=3x+6 (x∈R) 的反函数,我们从 y=3x+6中解得 x=-2 (y∈R),它也是一个函数.这样,函数 y=3x+6 (x∈R) 的反函数是 y=-2(x∈R).
函数 y=f(x) 的定义域 A 恰好是它的反函数 y=f-1(x) 的值域,函数 y=f(x) 的值域 B 恰好是它的反函数 y=f-1(x) 的定义域.
函数 y=ax与 y=logax 的图象表明,互为反函数的两个函数的图象关于直线 y=x 对称.
你能求出函数 y=log2(-1<x<1)的反函数吗
【思考】
函数 f(x)=x2 有反函数吗 为什么
提示:没有.
若令 y=f(x)=1,则 x=±1,
即x值不唯一,不符合反函数的定义.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) y=logx5是对数函数. ( )
(2) 对数函数的图象都过定点 ( )
(3) 对数函数的图象都在 y 轴的右侧. ( )
2. 函数 y=log2x 在区间 (0,2]上的最大值是 ( )
A.2 B.1 C.0 D. -1
B
解析:函数 y=log2x 在(0,2]上递增,故 x=2时,y的值最大,最大值是1.
解析
3. 函数 y=log3x与 y=log x 的图象关于________对称.
x轴
解析
解析:函数 y=log3x与 y=log x 的图象关于x轴对称.
4. 若对数函数f(x)的图象过点(4,-2),则f(8)=______.
-3
解析
解析:由题意设 f(x)=logax,则f(4)=loga4=-2,
所以 a-2=4,故 a=,即 f(x)=log x,
所以 f(8)=log x=-3.
5. 函数 f(x)= 的定义域为__________.
[2,+∞)
解析
解析:要使函数 f(x) 有意义,则 log2x-1≥0,
解得x≥2,即函数 f(x) 的定义域为[2,+∞).
1. 已知对数函数的图象过点M(9,2),则此对数函数的解析式为 ( )
A. y=log2x B. y=log3x
C. y=log x D. y=log x
【跟踪训练】
B
解析:设函数 f(x)=logax (x>0,a>0且a≠1),因为对数函数的图象过点M(9,2),所以 2=loga9,所以a2=9,a>0,解得a=3.所以此对数函数的解析式为 y=log3x.
解析
2. 函数 f(x) =ln(1-x) 的定义域是 ( )
A. (0,1) B. [0,1)
C. (1,+∞) D. (-∞,1)
D
解析:要使 f(x) 有意义,则1-x>0,
所以 x<1,所以 f(x) 的定义域为(-∞,1).
解析
3. 如果函数 y=log2x 的图象经过点 A (4,y0),那么
y0=________.
解析:因为函数 y=log2x 的图象经过点 A(4,y0),
所以 y0=log24,所以 2y0=4=22,
所以 y0=2.
解析
2
4. 设函数 f(x)=logax,则 f(a+1) 与 f(2) 的大小关系是
_____________.
解析:当a>1时,a+1>2,f(x)=logax 是增函数,则 f(a+1)>f(2);
当0<a<1时,a+1<2,f(x)=logax 是减函数,
则f(a+1)>f(2).
综上,f(a+1)>f(2).
解析
f(a+1)>f(2)
5. 若log0.1(1-a)>log0.1(2a-1),则a的取值范围是
___________.
<a<1
解析
解析:因为 y=log0.1x 是减函数且定义域为(0,+∞),所以 0<1-a<2a-1,即 解得 <a<1.
1-a<2a-1,
1-a >0,
习题 6.3
感受·理解
1. 画出函数 y=log4x 与 y= log x 的图象,指出这两个函
数图象之间的关系,并指出这两个函数性质的相同点
与不同点.
解 函数 y=log4x 与 y=log x
图象如图所示:
两个函数图象关于x轴对称,
相同性质:两个图象都位于y轴的右侧,都经过点(1,0),
这说明两个函数定义域都是(0,+∞),
且当x=1时,y=0,都不具有奇偶性,
值域都是R;
不同性质: y=log4x 在定义域内单调递增;y=log x 在定义域内单调递减.
2. 求下列函数的定义域:
(1) y=log2(5x+2);
(2) y=log (x-3);
解 根据题意可得 5x+2>0,解得 x>-,
则函数的定义域为(-,+∞).
解 根据题意可得 x-3>0,解得 x>3,
则函数的定义域为(3,+∞).
(3) y=ln(3x-1);
解 根据题意可得 3x-1>0,解得 x>,
则函数的定义域为(,+∞).
(4) y=log
解 根据题意可得 >0,解得 x>,
则函数的定义域为(,+∞).
3. 比较下列各组数中两个数的大小:
(1) log57.8,log57.9;
解 ∵ y=log5x是(0,+∞)上的单调递增函数,
且0<7.8<7.9.
∴ log57.8 < log57.9.
(2) log0.33,log0.32;
解 ∵y=log0.3x是(0,+∞)上的单调递增函数,
且0<2<3.
∴ log0.33 < log0.32.
(3) ln0.32,lg2;
解 ∵ y=lnx 是 (0,+∞) 上的单调递增函数,
且0<0.32<1,
∴ ln0.32<ln1=0,
∵ y=lgx 是 (0,+∞) 上的单调递增函数,
且0<1<2,
∴lg2>lg1=0,
∴ln 0.32<lg2.
(4) log55,log58.
解 ∵y=log6x 是(0,+∞)上的单调递增函数,
且0<5<6,
∴log65<log66=1.
∵y=log7x 是(0,+∞)上的单调递增函数,
且0<7<8,
∴log78>log77=1,
∴ log65<log78.
4. 证明:函数 y=log0.5(3x-2)在定义域上是减函数.
解 函数 y=f(x)=log0.5(3x-2)的定义域为(,+∞).
任取 <x1<x2,
则 f(x1)-f(x2)=log0.5(3x1-2) - log0.5(3x2-2)
= log0.5,
∵ <x1<x2,
∴ 3x1-2 < 3x2-2,
∴0 < < 1,
∴ log0.5 >log0.51=0,
∴ f(x1) - f(x2) > 0,即 f(x1) > f(x2),
∴函数 y=log0.5(3x-2) 在定义域(,+∞)上为减函数.
5. 解下列方程:
(1) 33x+5= 27;
解 ∵33x+5=27=33,
∴ 3x+5=3,即 x=-.
(2) 22x = 12;
解 ∵22x=12,
∴ 2x=log212,即 x=1+log23.
(3) 31-x-2=0.
解 ∵31-x-2=0,
∴ 1-x=log32,即 x=log3.
6. 画出函数 y=log2(x+1)与 y=log2(x-1)的图象,并指
出这两个函数图象之间的关系.
解 画出函数 y=log2(x+1) 与 y=log2(x-1) 的图象,如图所示:
从图象发现将 y=log2(x+1) 图象向右平移2个单位得 y= log2(x-1)的图象
7. 比较 log25与log58 的大小.
解 构造函数 y=log2x,x∈(0,+∞),
∵ y=log2x 在(0,+∞) 上单调递增,且 5>4,
∴ log25 > 1og24 = 2,
构造函数 y=log5x,x∈(0,+∞),
∵y=log5x 在(0,+∞) 上单调递增,且5<8<25,
∴1=log55 < log58< log25=2. ∴log25>1og58.
8. 设a与b为实数,a>0,a≠1. 已知函数
y=loga(x+b) 的图象如图所示求a与b
的值.
解 由图知,函数图象过点 (- 2,0) 和 (0,2),
a>0 且a≠1
所以 loga(-2+b)=0,
logab=2
a>0 且a≠1
即 -2+b=1,
a2=b
解得 a=,b=3.
9. 已知 f(x)=log3x,求证:
(1) f(x)+f(y) =f(xy);
证明:∵f(x)=log3x,
∴f(y)=log3y,
∴ f(xy)=log3(xy)=log3x+log3y=f(x)+f(y),
∴f(x)+f(y)=f(xy).
综上所述,结论是: f(x)+f(y)=f(xy).
(2) f(x)-f(y)=f( ).
证明:∵f(x)=log3x,
∴f( )=log3 =log3x-log3y=f(x)-f(y) ,
∴f(x) - f(y)=f ( ).
综上所述,结论是: f(x) - f(y)=f ( ).
10. 证明:函数 f(x)=lg(-1<x<1) 是奇数.
解 函数 f(x) 的定义域为(-1,1),关于原点对称,
f(-x)=lg =lg()-1=-lg =-f(x),
∴函数 f(x)=lg (-1<x<1) 是奇函数.
思考·运用
11. 设 a,b,c,d 均为不等于 1 的正实数,如图,已知
函数 y=logax,y=logbx,y=logcx,y=logdx 的图象
分别是曲线 C1,C2,C3,C4,
试判断 0,1,a,b,c,d 的大
小关系,并用“<”连接起来.
解 当对数函数值为1时,底数与真数相等,这是对数的一条重要性质,
将对数与指数结合更好理解,将对数 y=logax (a>0且a≠1)变为指数形式,ay=x (a>0且a≠1),
当 y=1 时,可得 a=x;
接下来作出y=1的直线与其他对数图象的交点根据横坐标的先后顺序,即可得到a、b、c、d、1、0的大小关系.
作直线 y=1 分别与 y=logax,y=logbx,y=logcx,y=logcx 的交点为 (a,1),(b,1),(c,1),(d,1) .
结合图象知 0<b<a<l<d<c.
12. 解下列方程:
(1) 21-x= 5;
解 原方程化为:21-x= 2log25,
∴1-x=log25,
∴原方程的解为: x=1-log25;
(2) 2×5x+1-9=0.
解 原方程化为:5x-1== 5 ,
∴x-1=log5,
∴原方程的解为: x=1+log5;
log5
13. 解下列不等式:
(1) 5x+2>2;
解 不等式 5x+2>2可化为 x+2>log52,
解得 x>-2+1og52,
∴不等式的解集为{ x∣x>-2+log52};
(2) 33-x<6;
解 不等式 33-x<6 可化为 3-x<1og36,
解得 x>3-1og36,
∴不等式的解集为{x∣x>3-log36}.
(3) log3(x+2)>3;
(4) lg(x-1) <1.
解 不等式 log3(x+2)>3 可化为 x+2>33,解得 x>25,
∴ 不等式的解集为{x∣x>25};
解 不等式 lg(x-1)<1可化为 解得1<x<11,
∴不等式的解集为 {x∣l<x<11}.
x-1>0
x-1<10,
探究·拓展
14. 已知函数 f(x)=lgx,对于任意的 ,x1,x2∈(0,+∞),
试比较 与f()的大小.
解: == =lg,
f()=lg ,
∵ x1,x2∈(0,+∞)
∴ ≥ 当且仅当 x1=x2 时,等号成立,
又 f(x)=lgx 在区间 (0,+∞) 上是增函数,
∴ lg lg,
即 ≤ f().
15. (探究题) 对于等式 ab=c (a>0,a≠1),如果将a视为
自变量x,b视为常数,c为关于a (即x) 的函数,记为 y,
那么y ,是幂函数;如果将 a 视为常数,b 视为自变
量x,c 为关于b (即x) 的函数,记为y,那么y=ax,是
指数函数;如果将 a 视为常数,c 视为自变量x,为关
于c (即x) 的函数,记为y,那么y=logax,是对数函数.
事实上,由这个等式还可以得到更多的函数模型.
例如,如果 c 为常数e (e 自然对数的底),将 a 视为自变量x (x>0,x≠1),则b为x的函数,记为 y,那么xy=e.
(1) 试将y表示成x的函数 f(x);
(2) 研究函数 f(x)的性质.
你还能运用这个等式得到什么样的函数 这些函数分别具有哪些性质
解:(1)易知 f(x)=.
(2) 函数 f(x) 的定义域为:(0,1) ∪(1,+∞);
值域为:(-∞,0)∪(0,+∞).
单调性:在 (0,1) 上单调递减,
在 (1,+∞) 上单调递减.
函数1:在ab=c中,令 c=e,b=x 视为自变量(x≠0),a=y 为关于x的函数则 yx=e y=e (x≠0).
此函数的定义域为:(-∞,0)∪(0,+∞),
值域为:(0,1)∪(1,+∞).
在 (-8,0) 上单调递减,在(0,+∞) 上单调递减.
函数2:在 ab=c中,将c视为自变量x,b视为常数3,a=y(a>0,且a≠1) 视为关于x的函数.
则 y3=x,y=,
定义域为:(0,1)∪(1,+∞),
值域为:(0,1)∪(1,+∞),
在(0,1),(1,+∞) 上单调递增.
问题与探究
钢琴与指数曲线
钢琴是一种用琴槌击弦而振动发声的键盘乐器,最早的钢琴是意大利佛罗伦萨梅迪奇宫廷的乐师克里斯托弗里(1655-1731)于1711年制造的,钢琴的意大利文为 piano forte,由 piano(弱)和 forte(强)两字组合而成.钢琴在音量上可以奏出极大的层次变化,它的音域极为宽广,最多可以有 7 个八度并包括所有的半音. 它可演奏和弦与复调音乐,手法极为丰富.因此,钢琴有“乐器之王”的称号.
但是,你曾留心过三角钢琴的轮廓有一段奇妙的“曲线”吗 三角钢琴的轮廓上部为什么要制成这样形状的曲线
为了解释这一现象,我们应学会观察、调查和研究.
首先,从左往右逐个试弹所有琴键(包括所有白键和黑键),我们听到琴声逐渐由低到高,这是因为琴声的高低与琴弦振动的频率有关,而琴弦振动的频率又与琴弦的长度有关,粗略地说,琴弦长则振动慢,频率小,故发出的声音低;琴弦短,则振动快,频率大,故发出的声音高.
如图 1,在 88 键钢琴中,音域宽度自大字二组的 A2 至小字五组的 c5. 根据“十二平均律”的法则,任何两个相邻的键所发出的音相差半音阶(100 音分),它们的振动频率之比是一个常数 Q. 设最低的第一个音 A2 的频率是a,则第二个音#A2,的频率是 aQ,第三个音 B2的频率是aQ2······另外,音高每提高八度(如 A2到 A1),频率增大为原来的2倍,
而八度音域内包含 12 个半音(连续的 7个白键和 5个黑键),所以,第十三个音(A1)的频率是第一个音(A2)的频率的2倍.故
aQ12 = 2a,
即 Q12=2.
另一方面,弦振动的频率与弦长成反比. 所以,从左向右,相邻两弦的长度之比是常数 q=,从而有 q12 = .
设左边第一根弦的长度为 l ,则第二根弦的长度为 lg,第三根弦的长度为 lq2······如图 2,取第一根弦所在直线为 y 轴,各弦靠近键盘的端点所在直线为 x 轴建立坐标系,相邻两弦间的距离为长度单位这时,将弦的另一端点(上部) 连成光滑曲线,那么曲线上任意点的坐标 (x,y)都满足函数关系 y=lgx.
若令 c=logql,则 y=lqx 可化为 y=qx+c.
经过适当平移,就可知道光滑曲线是指数函数 y=qx 的图象——指数曲线.
我国明代律学家朱载靖是世界上最早从理论上研究十二平均律的学者,他通过计算,使用
≈ 1.059 463 094 359 295 264 561 825,
现在人们通常取 ≈1.059 463,由此可见他的计算值在当时是比较精确的.
生活中到处都有数学,我们要学会用数学的眼光观察世界,用数学这一强大工具发现自然界的奥秘. 只要我们深入调查研究. 就能发现许多问题是可以利用数学知识加以解决的. 例如,中小学学生身高与课桌椅高度的关系.
许多学校的课桌椅高度都是一样的. 无疑,高度一样的课桌椅不仅制作方便,而且摆放起来整齐、美观.
但是,同一高度的课桌椅不能完全适合身高不同的学生,从而给他们的身体发育带来不良影响. 因此,中小学学生的身高与课桌椅高度的关系就值得研究.
通过实地调查,研究你所在学校的学生身高与课桌椅高度的关系.
阅 读
“怎样解题”表
《怎样解题》是由美国数学家和数学教育家 G.波利亚所写的一部畅销书,“怎样解题表”是该书的精华. 波利亚将解题过程分成了四个步骤,解题时按这四个步骤去尝试,有利于学会解题,提升分析问题与解决问题的能力.
第一, 你必须弄清问题 弄清问题
未知数是什么 已知数据是什么 条件是什么
满足条件是否可能 要确定未知数,条件是否充分 或者它是否不充分 或者是多余的 或者是矛盾的
画张图,引入适当的符号.
把条件的各个部分分开,你能否把它们写下来
第二, 找出已知数与未知数之间的联系. 如果找不出直接的联系,你可能不得不考虑辅助问题. 你应该最终得出一个求解的计划 拟订计划。
你以前见过它吗 你是否见过相同的问题而形式稍有不同
你是否知道与此有关的问题 你是否知道一个可能用得上的定理
看着未知数!试想出一个具有相同未知数或相似未知数的熟悉的问题.
这里有一个与你现在的问题有关,且早已解决的问题.
你能不能利用它 你能利用它的结果吗 你能利用它的方法吗 为了能利用它,你是否应该引入某些辅助元素
你能不能重新叙述这个问题 你能不能用不同的方法重新叙述它
回到定义去.
如果你不能解决所提出的问题,可先解决一个与此有关的问题.你能不能想出一个更容易着手的有关问题 一个更普遍的问题 一个更特殊的问题 一个类似的问题 你能否解决这个问题的一部分 仅仅保持条件的一部分而舍去其余部分,这样对于未知数能确定到什么程度 它会怎样变化 你能不能从已知数据导出某些有用的东西 你能不能想出适合于确定未知数的其他数据 如果需要的话,你能不能改变未知数或数据,或者二者都改变,以使新未知数和新数据彼此更接近
你是否利用了所有的已知数据 你是否利用了整个条件 你是否考虑了包含在问题中的所有必要的概念
第三, 实施你的计划 实现计划
实现你的求解计划,检验每一步骤.
你能否清楚地看出这一步骤是正确的 你能否证明这一步骤是正确的
第四, 验算所得到的解 回顾反思
你能否检验这个论证 你能否用别的方法导出这个结果 你能否一下子看出它来
你能不能把这个结果或方法用于其他的问题
本课结束
This lesson is over
THANKS!
第6章
幂函数指数函数和对数函数
6 . 3
对数函数
我们知道,在某细胞分裂过程中,细胞个数 y 是分裂次数 的指数函数 y=2x,因此,知道x的值 (输入值是分裂次数),就能求出y的值 (输出值是细胞个数). 现在,我们来研究相反的问题:知道了细胞个数 y,如何确定分裂次数x
为了求 y=2x 中的x,我们将 y=2x 改写成对数式为
x=log2y .
对于每一个给定的y值,都有唯一的值与之对应把y看作自变量, 就是 y 的函数. 这样就得到了一个新的函数.
前面提到的放射性物质,经过的时间 x (单位:年) 与物质剩留量 y 的关系式为
y=0.84x
改写成对数式为
x=log0.84y.
类似地,y 是自变量,x 是 y 的函数.
习惯上,仍用 x 表示自变量,用 y 表示它的函数. 这样,上面两个函数就分别写成 y=log2x 和 y=log0.84x.
类似还可以得到函数 y=log3x,y=log x 等.
● 函数 y=log2x,y=log0.84x,y=log3x,y=log x 具有
什么共同特征
这些函数的表达式都是对数的形式,底数是常数,真数是自变量,这样的函数称为对数函数.
一、对数函数
一般地,
函数
y=logax (a>0,a≠1)
叫作对数函数,它的定义域是(0,+∞).
提示:① a>0,且 a≠1;
② logax 的系数为1;
③自变量x的系数为1.
【思考】
对数函数解析式有什么特征
在图6-3-1中,我们同时画出了对数函数 y=log2x,y=lgx,y=log x 的图象.
观察图 6-3-1中的函数的图象,对照指数函数的性质,你发现对数函数 y=logax (a>0,a≠1) 有哪些性质
二、对数函数的图象与性质
a>1 0<a<1
图象
性质 (1) 定义域: ___________
(0,+∞)
a>1 0<a<1
性质 (2) 值域: R
(3) 图象过点(1,0)
(4) 在(0,+∞)上是增函数; 当0<x<1时,y<0; 当x>1时,y>0. 在(0,+∞)上是减函数;
当0<x<1时,y>0;
当x>1时,y<0.
【思考】
提示:当 x=1 时,loga1=0 恒成立,即对数函数的图象一定过点 (1,0) .
对于对数函数y=log2x,y=log3x,y=log x,y=log x,
···,为什么一定过点(1,0)
思 考
函数 y=logax 与函数 y=ax(a>0,a≠1)的定义域、值域之间有怎样的关系
画出下列两组函数的图象,并观察各组函数的图象,寻找它们之间的关系:
(1) y=2x,y=log2x;
(2) y=()x,y=log x.
由图可以看出,函数 y=2x与y=log2x 的图象关于直线 y=x 对称,函数 y=()x与 y=log x 的图象也关于直线 y=x 对称.
思 考
一般地,当a>0,a≠1时,函数 y=ax与 y=logax 的图象有怎样的关系
当 a>0,a≠1 时,y=logax 称为 y=ax 的反函数. 反之,y=ax 也称为 y=logax 的反函数.
一般地,如果函数 y=f(x) 存在反函数,那么它的反函数记作 y=f-1(x).
例 1
求下列函数的定义域:
(1) y=log0.2(4-x);
解: 当4-x>0,即x<4时,log0.2(4-x)有意义;
当 x≥4 时,log0.2(4-x)没有意义.
因此,函数 y=log0.2(4-x)的定义域是(-∞,4).
(2) y=loga (a>0,a≠1).
解:当>0,即 x>1时, loga有意义;
当 x≤1 时,loga 没有意义.
因此,函数 y=loga的定义域是(1,+∞).
例 2
比较下列各组数中两个数的大小:
(1) log23.4,log23.8;
解 考察对数函数 y=log2x.
因为 2>1,
所以 y=log2x 在区间(0,+∞)上是增函数.
又因为 0<3.4<3.8,
所以 log23.4<log23.8.
(2) log0.51.8,log0.52.1;
解 考察对数函数 y=log0.5x.
因为0<0.5<1,
所以 y=log0.5x 在区间(0,+∞)上是减函数.
又因为 0<1.8< 2.1,
所以 log0.51.8 > log0.52.1.
解 考察对数函数 y=log7x.
因为 7>1,
所以 y=log7x 在区间(0,+∞)上是增函数.
又因为 0<5<7,
所以 log75 < log77=1.
同理 log67 > log66=1,
所以 log75 < log67.
(3) 1og75,log67.
例 3
说明函数 y=log3(x+2) 与函数 y=log3x 的图的关系.
解 比较函数 y=log3(x+2)与 y =log3x 的取值关系,列表如表 6-3-2 所示.
一般地,函数 y=log3(x+2)中x=a-2 对应的 y 值与函数y=log3x中x=a对应的y值相等,则将对数函数 y=log3x 的图象向左平移2个单位长度,就得到函数y=log3(x+2) 的图象.
这两个函数的图象如图所示.
思 考
函数 y=log(x+b) 与函数 y=logax (a>0,a≠1,b≠0)的图象之间有怎样的关系
例 4
画出函数 y=log2∣x∣的图象,并根据图象写出函数的单调区间.
解:由于函数 y=f(x)=log2∣x∣满足对任意的 x∈(-8,0)∪(0,+∞) 都有
f(-x) = log2∣-x∣=log2∣x∣=f(x),
所以函数 y=log2∣x∣是偶函数,它的图象关于y轴对称.
当x>0时,log2∣x∣=lg2x. 因此,我们先画出函数 y=log2x (x>0)的图象C1,再作出 C1关于 y 轴对称的图象C2. C1和C2构成函数 y=log2∣x∣的图象,如图 6-3-4.
由图象可以知道,函数 y=log2∣x∣的减区间是(-∞ ,0),增区间是(0,+∞).
信息技术
在GGB中作出动态函数 y=ax与y=logax (a>0,a≠1)的图象,直观地理解第 145 页“思考”中的问题.
(1) 在输入框中输入“y=a∧x”,确认“创建滑动条:a”(图6-3-5)
(2) 在输入框中输入“y=log(a,x)”,敲回车确认;
(3) 拖动滑块a,观察两个图象的动态变化趋势 (图 6-3-6).
右击滑块 a 在“属性”中可设置参数 a 的范围及增量(每次变化的幅度).
练 习
1. 画出函数 y=log3x;与 y=log x 的图象,指出这两个函数图象之间的关系.
函数 y=log3x 在(0, +∞)上单调递增,且图象过点(1,0).
函数 y=log x 在(0,+∞)上单调递减,且图象过点(1,0).
log x=log3-1x=-log3x ,
两个函数的图象关于x轴对称
2. 求下列函数的定义域:
(1) y=log2(2x+1);
解 要使函数 y=log3(2x+1) 有意义,需满足2x+1>0,
解得 x>-,
故函数 y=log2(2x+1) 的定义域为(-,+∞);
(2) y=log0.5(2x-3)
解 要使函数y=log0.5(2x-3)有意义,需满足2x-3>0,
即 x>,
故函数 y=log0.5(2x-3)的定义域为(,+∞);
(3) y=log (2-x);
解 要使函数y=log (2-x) 有意义,
需满足2-x>0,
解得 x<2,
故函数 y= log (2-x)的定义域为(-∞ ,2);
(4) y=lg.
解 要使函数y=lg 有意义,需满足x-1>0,
解得 x>1,
故函数 y=lg 的定义域为(1,+∞);
3. 判断下列函数的单调性:
(1) y=log2x;
(2) y=log x;
解 ∵函数 y=log2x,x>0 的底数2>1,
∴该函数在 (0,+∞) 上单调递增;
解 ∵函数 y=log x,x>0 的底数0<<1,
∴该函数在 (0,+∞) 上单调递减;
(3) y=log7(2x+1);
解 ∵ 2x+1>0,∴x>-,
设 t=2x+1,则 y=log7t,t>-,
∵函数 t=2x+1 在(-,+∞)上单调递增,
且函数 y=log7t 在(0,+∞) 上单调递增,
∴由复合函数的单调性的“同增异减”性可得,
y=log7(2x+1)在(-,+∞)上单调递增;
(4) y=lg(3-2x).
解 ∵ 3-2x>0,∴x<,
设 t=3-2x,则 y=lgt,
∵函数 t=3-2x 在(-∞ ,)上单调递减,
且函数 y=lgt 在(0,+∞) 上单调递增,
∴由复合函数的单调性的“同增异减”性可得,
y=lg(3-2x)在(-∞ ,)上单调递减;
4. 比较下列各组数中两个数的大小:
(1) log35.4,log35.5;
(2) log π,log e;
解 ∵f(x)=log3x 在(0,+∞) 单调递增,且 5.4<5.5,
∴log35.4<log35.5;
解 ∵f(x)=log x 在(0,+∞) 单调递减,且 π>e,
∴log π<log e;
(3) lg 0.02,lg 3.12;
(4) ln 0.55,ln 0.56.
解 ∵f(x)=lgx 在(0,+∞) 单调递增,且 0.02<3.12,
∴lg0.02<lg3.12;
解 ∵f(x)=lnx 在(0,+∞) 单调递增,且 0.55<0.56,
∴ln0.55<ln0.56;
5. 解下列方程:
(1) log2(3x)=log2(2x+1);
解 ∵log2(3x)=log2(2a+1),
∴ 3x=2x+1,
即x=1.
(2) log5(2x+1) =log5(x2-2);
解 ∵ log5(2x+1)=log5(x2-2),
∴ 2x+1=x2-2,
∴ x=3 或 x=-1,
又∵真数都是大于0的,
当x=-1时,x2-2=-1<0.
∴x=-1舍去,即 x=3.
(3) lg = lg(x-1).
解 ∵lg = lg(x-1),
∴ = x-1 且x-1>0,
∴ x=2.
链 接
我们已经知道,函数 y=ax与y=logax (a>0,a≠1) 互为反函数. 一般地,设 A,B 分别为函数y=f(x)的定义域和值域,如果由函数y=f(x)可解得唯一 x=(y) 也是一个函数 (即对任意一个 y∈B,都有唯一的 x∈A 与之对应),那么就称函数 x=(y) 是函数 y=f(x) 的反函数,记作 x=f -1(y).
在 x=f-1(y)中,y 是自变量,x是y的函数. 习惯上改写成 y=f-1(x) (x∈B,y∈A) 的形式.
例如,求函数 y=3x+6 (x∈R) 的反函数,我们从 y=3x+6中解得 x=-2 (y∈R),它也是一个函数.这样,函数 y=3x+6 (x∈R) 的反函数是 y=-2(x∈R).
函数 y=f(x) 的定义域 A 恰好是它的反函数 y=f-1(x) 的值域,函数 y=f(x) 的值域 B 恰好是它的反函数 y=f-1(x) 的定义域.
函数 y=ax与 y=logax 的图象表明,互为反函数的两个函数的图象关于直线 y=x 对称.
你能求出函数 y=log2(-1<x<1)的反函数吗
【思考】
函数 f(x)=x2 有反函数吗 为什么
提示:没有.
若令 y=f(x)=1,则 x=±1,
即x值不唯一,不符合反函数的定义.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) y=logx5是对数函数. ( )
(2) 对数函数的图象都过定点 ( )
(3) 对数函数的图象都在 y 轴的右侧. ( )
2. 函数 y=log2x 在区间 (0,2]上的最大值是 ( )
A.2 B.1 C.0 D. -1
B
解析:函数 y=log2x 在(0,2]上递增,故 x=2时,y的值最大,最大值是1.
解析
3. 函数 y=log3x与 y=log x 的图象关于________对称.
x轴
解析
解析:函数 y=log3x与 y=log x 的图象关于x轴对称.
4. 若对数函数f(x)的图象过点(4,-2),则f(8)=______.
-3
解析
解析:由题意设 f(x)=logax,则f(4)=loga4=-2,
所以 a-2=4,故 a=,即 f(x)=log x,
所以 f(8)=log x=-3.
5. 函数 f(x)= 的定义域为__________.
[2,+∞)
解析
解析:要使函数 f(x) 有意义,则 log2x-1≥0,
解得x≥2,即函数 f(x) 的定义域为[2,+∞).
1. 已知对数函数的图象过点M(9,2),则此对数函数的解析式为 ( )
A. y=log2x B. y=log3x
C. y=log x D. y=log x
【跟踪训练】
B
解析:设函数 f(x)=logax (x>0,a>0且a≠1),因为对数函数的图象过点M(9,2),所以 2=loga9,所以a2=9,a>0,解得a=3.所以此对数函数的解析式为 y=log3x.
解析
2. 函数 f(x) =ln(1-x) 的定义域是 ( )
A. (0,1) B. [0,1)
C. (1,+∞) D. (-∞,1)
D
解析:要使 f(x) 有意义,则1-x>0,
所以 x<1,所以 f(x) 的定义域为(-∞,1).
解析
3. 如果函数 y=log2x 的图象经过点 A (4,y0),那么
y0=________.
解析:因为函数 y=log2x 的图象经过点 A(4,y0),
所以 y0=log24,所以 2y0=4=22,
所以 y0=2.
解析
2
4. 设函数 f(x)=logax,则 f(a+1) 与 f(2) 的大小关系是
_____________.
解析:当a>1时,a+1>2,f(x)=logax 是增函数,则 f(a+1)>f(2);
当0<a<1时,a+1<2,f(x)=logax 是减函数,
则f(a+1)>f(2).
综上,f(a+1)>f(2).
解析
f(a+1)>f(2)
5. 若log0.1(1-a)>log0.1(2a-1),则a的取值范围是
___________.
<a<1
解析
解析:因为 y=log0.1x 是减函数且定义域为(0,+∞),所以 0<1-a<2a-1,即 解得 <a<1.
1-a<2a-1,
1-a >0,
习题 6.3
感受·理解
1. 画出函数 y=log4x 与 y= log x 的图象,指出这两个函
数图象之间的关系,并指出这两个函数性质的相同点
与不同点.
解 函数 y=log4x 与 y=log x
图象如图所示:
两个函数图象关于x轴对称,
相同性质:两个图象都位于y轴的右侧,都经过点(1,0),
这说明两个函数定义域都是(0,+∞),
且当x=1时,y=0,都不具有奇偶性,
值域都是R;
不同性质: y=log4x 在定义域内单调递增;y=log x 在定义域内单调递减.
2. 求下列函数的定义域:
(1) y=log2(5x+2);
(2) y=log (x-3);
解 根据题意可得 5x+2>0,解得 x>-,
则函数的定义域为(-,+∞).
解 根据题意可得 x-3>0,解得 x>3,
则函数的定义域为(3,+∞).
(3) y=ln(3x-1);
解 根据题意可得 3x-1>0,解得 x>,
则函数的定义域为(,+∞).
(4) y=log
解 根据题意可得 >0,解得 x>,
则函数的定义域为(,+∞).
3. 比较下列各组数中两个数的大小:
(1) log57.8,log57.9;
解 ∵ y=log5x是(0,+∞)上的单调递增函数,
且0<7.8<7.9.
∴ log57.8 < log57.9.
(2) log0.33,log0.32;
解 ∵y=log0.3x是(0,+∞)上的单调递增函数,
且0<2<3.
∴ log0.33 < log0.32.
(3) ln0.32,lg2;
解 ∵ y=lnx 是 (0,+∞) 上的单调递增函数,
且0<0.32<1,
∴ ln0.32<ln1=0,
∵ y=lgx 是 (0,+∞) 上的单调递增函数,
且0<1<2,
∴lg2>lg1=0,
∴ln 0.32<lg2.
(4) log55,log58.
解 ∵y=log6x 是(0,+∞)上的单调递增函数,
且0<5<6,
∴log65<log66=1.
∵y=log7x 是(0,+∞)上的单调递增函数,
且0<7<8,
∴log78>log77=1,
∴ log65<log78.
4. 证明:函数 y=log0.5(3x-2)在定义域上是减函数.
解 函数 y=f(x)=log0.5(3x-2)的定义域为(,+∞).
任取 <x1<x2,
则 f(x1)-f(x2)=log0.5(3x1-2) - log0.5(3x2-2)
= log0.5,
∵ <x1<x2,
∴ 3x1-2 < 3x2-2,
∴0 < < 1,
∴ log0.5 >log0.51=0,
∴ f(x1) - f(x2) > 0,即 f(x1) > f(x2),
∴函数 y=log0.5(3x-2) 在定义域(,+∞)上为减函数.
5. 解下列方程:
(1) 33x+5= 27;
解 ∵33x+5=27=33,
∴ 3x+5=3,即 x=-.
(2) 22x = 12;
解 ∵22x=12,
∴ 2x=log212,即 x=1+log23.
(3) 31-x-2=0.
解 ∵31-x-2=0,
∴ 1-x=log32,即 x=log3.
6. 画出函数 y=log2(x+1)与 y=log2(x-1)的图象,并指
出这两个函数图象之间的关系.
解 画出函数 y=log2(x+1) 与 y=log2(x-1) 的图象,如图所示:
从图象发现将 y=log2(x+1) 图象向右平移2个单位得 y= log2(x-1)的图象
7. 比较 log25与log58 的大小.
解 构造函数 y=log2x,x∈(0,+∞),
∵ y=log2x 在(0,+∞) 上单调递增,且 5>4,
∴ log25 > 1og24 = 2,
构造函数 y=log5x,x∈(0,+∞),
∵y=log5x 在(0,+∞) 上单调递增,且5<8<25,
∴1=log55 < log58< log25=2. ∴log25>1og58.
8. 设a与b为实数,a>0,a≠1. 已知函数
y=loga(x+b) 的图象如图所示求a与b
的值.
解 由图知,函数图象过点 (- 2,0) 和 (0,2),
a>0 且a≠1
所以 loga(-2+b)=0,
logab=2
a>0 且a≠1
即 -2+b=1,
a2=b
解得 a=,b=3.
9. 已知 f(x)=log3x,求证:
(1) f(x)+f(y) =f(xy);
证明:∵f(x)=log3x,
∴f(y)=log3y,
∴ f(xy)=log3(xy)=log3x+log3y=f(x)+f(y),
∴f(x)+f(y)=f(xy).
综上所述,结论是: f(x)+f(y)=f(xy).
(2) f(x)-f(y)=f( ).
证明:∵f(x)=log3x,
∴f( )=log3 =log3x-log3y=f(x)-f(y) ,
∴f(x) - f(y)=f ( ).
综上所述,结论是: f(x) - f(y)=f ( ).
10. 证明:函数 f(x)=lg(-1<x<1) 是奇数.
解 函数 f(x) 的定义域为(-1,1),关于原点对称,
f(-x)=lg =lg()-1=-lg =-f(x),
∴函数 f(x)=lg (-1<x<1) 是奇函数.
思考·运用
11. 设 a,b,c,d 均为不等于 1 的正实数,如图,已知
函数 y=logax,y=logbx,y=logcx,y=logdx 的图象
分别是曲线 C1,C2,C3,C4,
试判断 0,1,a,b,c,d 的大
小关系,并用“<”连接起来.
解 当对数函数值为1时,底数与真数相等,这是对数的一条重要性质,
将对数与指数结合更好理解,将对数 y=logax (a>0且a≠1)变为指数形式,ay=x (a>0且a≠1),
当 y=1 时,可得 a=x;
接下来作出y=1的直线与其他对数图象的交点根据横坐标的先后顺序,即可得到a、b、c、d、1、0的大小关系.
作直线 y=1 分别与 y=logax,y=logbx,y=logcx,y=logcx 的交点为 (a,1),(b,1),(c,1),(d,1) .
结合图象知 0<b<a<l<d<c.
12. 解下列方程:
(1) 21-x= 5;
解 原方程化为:21-x= 2log25,
∴1-x=log25,
∴原方程的解为: x=1-log25;
(2) 2×5x+1-9=0.
解 原方程化为:5x-1== 5 ,
∴x-1=log5,
∴原方程的解为: x=1+log5;
log5
13. 解下列不等式:
(1) 5x+2>2;
解 不等式 5x+2>2可化为 x+2>log52,
解得 x>-2+1og52,
∴不等式的解集为{ x∣x>-2+log52};
(2) 33-x<6;
解 不等式 33-x<6 可化为 3-x<1og36,
解得 x>3-1og36,
∴不等式的解集为{x∣x>3-log36}.
(3) log3(x+2)>3;
(4) lg(x-1) <1.
解 不等式 log3(x+2)>3 可化为 x+2>33,解得 x>25,
∴ 不等式的解集为{x∣x>25};
解 不等式 lg(x-1)<1可化为 解得1<x<11,
∴不等式的解集为 {x∣l<x<11}.
x-1>0
x-1<10,
探究·拓展
14. 已知函数 f(x)=lgx,对于任意的 ,x1,x2∈(0,+∞),
试比较 与f()的大小.
解: == =lg,
f()=lg ,
∵ x1,x2∈(0,+∞)
∴ ≥ 当且仅当 x1=x2 时,等号成立,
又 f(x)=lgx 在区间 (0,+∞) 上是增函数,
∴ lg lg,
即 ≤ f().
15. (探究题) 对于等式 ab=c (a>0,a≠1),如果将a视为
自变量x,b视为常数,c为关于a (即x) 的函数,记为 y,
那么y ,是幂函数;如果将 a 视为常数,b 视为自变
量x,c 为关于b (即x) 的函数,记为y,那么y=ax,是
指数函数;如果将 a 视为常数,c 视为自变量x,为关
于c (即x) 的函数,记为y,那么y=logax,是对数函数.
事实上,由这个等式还可以得到更多的函数模型.
例如,如果 c 为常数e (e 自然对数的底),将 a 视为自变量x (x>0,x≠1),则b为x的函数,记为 y,那么xy=e.
(1) 试将y表示成x的函数 f(x);
(2) 研究函数 f(x)的性质.
你还能运用这个等式得到什么样的函数 这些函数分别具有哪些性质
解:(1)易知 f(x)=.
(2) 函数 f(x) 的定义域为:(0,1) ∪(1,+∞);
值域为:(-∞,0)∪(0,+∞).
单调性:在 (0,1) 上单调递减,
在 (1,+∞) 上单调递减.
函数1:在ab=c中,令 c=e,b=x 视为自变量(x≠0),a=y 为关于x的函数则 yx=e y=e (x≠0).
此函数的定义域为:(-∞,0)∪(0,+∞),
值域为:(0,1)∪(1,+∞).
在 (-8,0) 上单调递减,在(0,+∞) 上单调递减.
函数2:在 ab=c中,将c视为自变量x,b视为常数3,a=y(a>0,且a≠1) 视为关于x的函数.
则 y3=x,y=,
定义域为:(0,1)∪(1,+∞),
值域为:(0,1)∪(1,+∞),
在(0,1),(1,+∞) 上单调递增.
问题与探究
钢琴与指数曲线
钢琴是一种用琴槌击弦而振动发声的键盘乐器,最早的钢琴是意大利佛罗伦萨梅迪奇宫廷的乐师克里斯托弗里(1655-1731)于1711年制造的,钢琴的意大利文为 piano forte,由 piano(弱)和 forte(强)两字组合而成.钢琴在音量上可以奏出极大的层次变化,它的音域极为宽广,最多可以有 7 个八度并包括所有的半音. 它可演奏和弦与复调音乐,手法极为丰富.因此,钢琴有“乐器之王”的称号.
但是,你曾留心过三角钢琴的轮廓有一段奇妙的“曲线”吗 三角钢琴的轮廓上部为什么要制成这样形状的曲线
为了解释这一现象,我们应学会观察、调查和研究.
首先,从左往右逐个试弹所有琴键(包括所有白键和黑键),我们听到琴声逐渐由低到高,这是因为琴声的高低与琴弦振动的频率有关,而琴弦振动的频率又与琴弦的长度有关,粗略地说,琴弦长则振动慢,频率小,故发出的声音低;琴弦短,则振动快,频率大,故发出的声音高.
如图 1,在 88 键钢琴中,音域宽度自大字二组的 A2 至小字五组的 c5. 根据“十二平均律”的法则,任何两个相邻的键所发出的音相差半音阶(100 音分),它们的振动频率之比是一个常数 Q. 设最低的第一个音 A2 的频率是a,则第二个音#A2,的频率是 aQ,第三个音 B2的频率是aQ2······另外,音高每提高八度(如 A2到 A1),频率增大为原来的2倍,
而八度音域内包含 12 个半音(连续的 7个白键和 5个黑键),所以,第十三个音(A1)的频率是第一个音(A2)的频率的2倍.故
aQ12 = 2a,
即 Q12=2.
另一方面,弦振动的频率与弦长成反比. 所以,从左向右,相邻两弦的长度之比是常数 q=,从而有 q12 = .
设左边第一根弦的长度为 l ,则第二根弦的长度为 lg,第三根弦的长度为 lq2······如图 2,取第一根弦所在直线为 y 轴,各弦靠近键盘的端点所在直线为 x 轴建立坐标系,相邻两弦间的距离为长度单位这时,将弦的另一端点(上部) 连成光滑曲线,那么曲线上任意点的坐标 (x,y)都满足函数关系 y=lgx.
若令 c=logql,则 y=lqx 可化为 y=qx+c.
经过适当平移,就可知道光滑曲线是指数函数 y=qx 的图象——指数曲线.
我国明代律学家朱载靖是世界上最早从理论上研究十二平均律的学者,他通过计算,使用
≈ 1.059 463 094 359 295 264 561 825,
现在人们通常取 ≈1.059 463,由此可见他的计算值在当时是比较精确的.
生活中到处都有数学,我们要学会用数学的眼光观察世界,用数学这一强大工具发现自然界的奥秘. 只要我们深入调查研究. 就能发现许多问题是可以利用数学知识加以解决的. 例如,中小学学生身高与课桌椅高度的关系.
许多学校的课桌椅高度都是一样的. 无疑,高度一样的课桌椅不仅制作方便,而且摆放起来整齐、美观.
但是,同一高度的课桌椅不能完全适合身高不同的学生,从而给他们的身体发育带来不良影响. 因此,中小学学生的身高与课桌椅高度的关系就值得研究.
通过实地调查,研究你所在学校的学生身高与课桌椅高度的关系.
阅 读
“怎样解题”表
《怎样解题》是由美国数学家和数学教育家 G.波利亚所写的一部畅销书,“怎样解题表”是该书的精华. 波利亚将解题过程分成了四个步骤,解题时按这四个步骤去尝试,有利于学会解题,提升分析问题与解决问题的能力.
第一, 你必须弄清问题 弄清问题
未知数是什么 已知数据是什么 条件是什么
满足条件是否可能 要确定未知数,条件是否充分 或者它是否不充分 或者是多余的 或者是矛盾的
画张图,引入适当的符号.
把条件的各个部分分开,你能否把它们写下来
第二, 找出已知数与未知数之间的联系. 如果找不出直接的联系,你可能不得不考虑辅助问题. 你应该最终得出一个求解的计划 拟订计划。
你以前见过它吗 你是否见过相同的问题而形式稍有不同
你是否知道与此有关的问题 你是否知道一个可能用得上的定理
看着未知数!试想出一个具有相同未知数或相似未知数的熟悉的问题.
这里有一个与你现在的问题有关,且早已解决的问题.
你能不能利用它 你能利用它的结果吗 你能利用它的方法吗 为了能利用它,你是否应该引入某些辅助元素
你能不能重新叙述这个问题 你能不能用不同的方法重新叙述它
回到定义去.
如果你不能解决所提出的问题,可先解决一个与此有关的问题.你能不能想出一个更容易着手的有关问题 一个更普遍的问题 一个更特殊的问题 一个类似的问题 你能否解决这个问题的一部分 仅仅保持条件的一部分而舍去其余部分,这样对于未知数能确定到什么程度 它会怎样变化 你能不能从已知数据导出某些有用的东西 你能不能想出适合于确定未知数的其他数据 如果需要的话,你能不能改变未知数或数据,或者二者都改变,以使新未知数和新数据彼此更接近
你是否利用了所有的已知数据 你是否利用了整个条件 你是否考虑了包含在问题中的所有必要的概念
第三, 实施你的计划 实现计划
实现你的求解计划,检验每一步骤.
你能否清楚地看出这一步骤是正确的 你能否证明这一步骤是正确的
第四, 验算所得到的解 回顾反思
你能否检验这个论证 你能否用别的方法导出这个结果 你能否一下子看出它来
你能不能把这个结果或方法用于其他的问题
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
