第二十九章 投影与视图 达标测评卷(含答案)
文档属性
| 名称 | 第二十九章 投影与视图 达标测评卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 05:24:36 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第二十九章 投影与视图达标测评卷
一、选择题(本题共计10小题,每题3分,共计30分)
1.下列投影现象属于平行投影的是 ( )
A.太阳光发出的光线所形成的投影
B.手电筒发出的光线所形成的投影
C.路灯发出的光线所形成的投影
D.台灯发出的光线所形成的投影
2.下面属于中心投影的是 ( )
A.太阳光下的树影 B.皮影戏—
C.月光下房屋的影子 D.海上日出
3.从早上太阳升起的某一时刻开始到晚上,旭日广场的旗杆在地面上的影子的变化规律是 ( )
A.先变长,后变短 B.先变短,后变长
C.方向改变,长短不变 D.以上都不正确
4.如图,属于“物体在太阳光下形成的影子”的图形是 ( )
5.如图,光线由上向下照射正五棱柱时的正投影是 ( )
6.如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为2:5,且三角板的一边长为8cm .则投影三角板的对应边长为 ( )
A.20 cm B.10 cm C.8 cm D.3. 2cm
7.如图,路灯距地面8米,身高1.6米的小明从距离灯底(点 O)20米的点A处,沿AO所在的直线行走12米到达点B时,小明身影长度 ( )
A.变长2.5米 B.变短2米
C.变短3米 D.变短2.5米
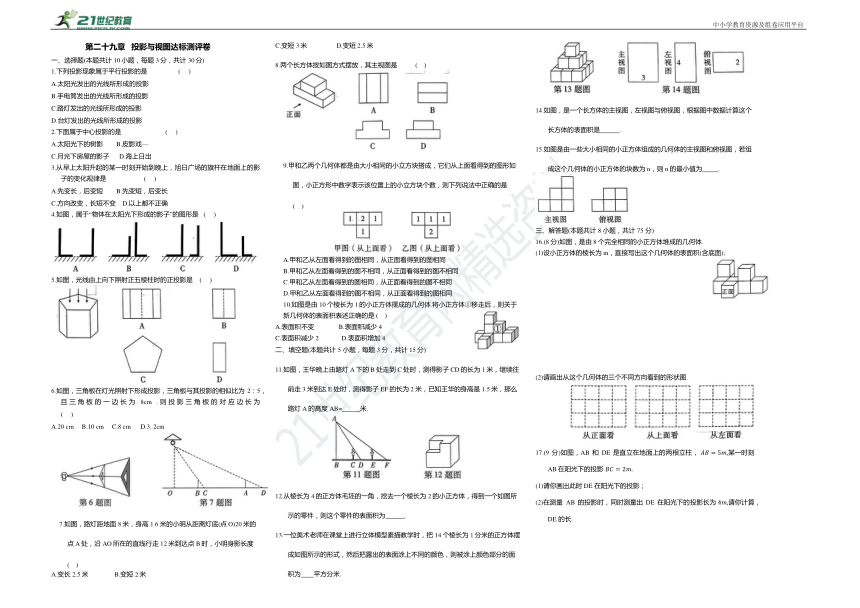
8.两个长方体按如图方式摆放,其主视图是 ( )
9.甲和乙两个几何体都是由大小相同的小立方块搭成,它们从上面看得到的图形如图,小正方形中数字表示该位置上的小立方块个数,则下列说法中正确的是 ( )
A.甲和乙从左面看得到的图相同,从正面看得到的图相同
B.甲和乙从左面看得到的图不相同,从正面看得到的图不相同
C.甲和乙从左面看得到的图相同,从正面看得到的图不相同
D.甲和乙从左面看得到的图不相同,从正面看得到的图相同
10.如图是由 10个棱长为1的小正方体摆成的几何体.将小正方体①移走后,则关于新几何体的表面积表述正确的是 ( )
A.表面积不变 B.表面积减少4
C.表面积减少2 D.表面积增加4
二、填空题(本题共计5 小题,每题3 分,共计15分)
11.如图,王华晚上由路灯A下的B处走到C 处时,测得影子 CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB= 米.
12.从棱长为4的正方体毛坯的一角,挖去一个棱长为2的小正方体,得到一个如图所示的零件,则这个零件的表面积为 .
13.一位美术老师在课堂上进行立体模型素描教学时,把14个棱长为1分米的正方体摆成如图所示的形式,然后把露出的表面涂上不同的颜色,则被涂上颜色部分的面积为 平方分米.
14.如图,是一个长方体的主视图,左视图与俯视图,根据图中数据计算这个长方体的表面积是 .
15.如图是由一些大小相同的小正方体组成的几何体的主视图和俯视图,若组成这个几何体的小正方体的块数为n,则n的最小值为 .
三、解答题(本题共计8 小题,共计75 分)
16.(8分)如图,是由8个完全相同的小正方体堆成的几何体.
(1)设小正方体的棱长为 m,直接写出这个几何体的表面积(含底面);
(2)请画出从这个几何体的三个不同方向看到的形状图.
17.(9分)如图,AB 和 DE是直立在地面上的两根立柱, 某一时刻AB在阳光下的投影
(1)请你画出此时 DE 在阳光下的投影;
(2)在测量AB的投影时,同时测量出 DE 在阳光下的投影长为 请你计算,DE 的长.
18.(9分)如图,身高1.5米的小明(AB)在太阳光下的影子AG长1.8米,此时,立柱CD的影子一部分落在地面CE上,一部分落在墙 EF 上.
(1)请你在墙上画出表示 CD 的部分影子 EH.;
(2)若量得( 米, 米,求立柱CD的高.
19.(10分)如图所示的是一个几何体的三视图.
(1)该几何体是 ;(填几何体的名称)
(2)求出这个几何体的体积.
20.(9 分)如图所示是一个几何体的主视图和俯视图,求该几何体的体积及其表面积(保留 π).
21.(10分)如图,是一个几何体从三个方向看所得到的形状图:
(1)写出这个几何体的名称;
(2)画出它的一种表面展开图;
(3)若从正面看长方形的高为3cm,从上面看三角形的边长为2cm ,求这个几何体的侧面积.
22.(9分)如图是一颗骰子的三种不同的放置方法.
(1)根据图中三种放置方法,推出“ ”处的点数;
(2)求这三个骰子下底面上的点数和.
23.(11 分)一个物体是由棱长为3c m的正方体模型堆砌而成的,其形状从三个方向看如图所示:
(1)请在从上面看到的形状图上标出每个位置中小正方体的个数;
(2)求出该物体的体积是多少;
(3)该物体的表面积是多少
1-10ABBDC ACDDC
11.6.
12.96 【解析】利用平移的方法,从棱长为4的正方体毛坯的一角,挖去一个棱长为2 的小正方体后所得几何体的表面积与原正方体的表面积相同.这个零件的表面积=6×4×4=96.
13.33 【解析】根据分析露出的面积为4×(1+2+3)+9=33(dm ),即涂上颜色的面积为33dm .故答案为33.
14.52
15.8 【解析】根据主视图和俯视图可知,该几何体中小正方体数最少的分布情况如下:
∴n=1+1+2+1+3=8.
故答案为8.
16.解:
(2)如图:
17.解:(1)连接AC,过点 D 作 DF∥AC,则 EF 为所求;
(2)∵AC∥DF,∴ ∠ACB=∠DFE,
又∠ABC=∠DEF=90°,
.. Rt△ABC∽Rt△DEF,
即 解得DE=10,
即 DE 的长为 10 m.
18.解:(1)如图,线段 EH为所求;
(2)过点E作EM∥BG,交CD于点M,则四边形 DHEM 是平行四边形,
即 DM=EH=1.5米,
解得 CM=1,
∴CD=CM+DM=1+1.5=2.5(米),
故立柱 CD 的高为2.5 米.
19.解:(1)由三视图可知该几何体的形状是三棱柱,故答案为三棱柱;
(2)由俯视图可知该三棱柱底面是等腰三角形,由主视图可知底面三角形底边为1+1=2,三棱柱高为2,
由左视图可知底面三角形高为1,故该几何体的体积为
20.解:由主视图和俯视图可知,该几何体是一个组合体,其上部分是一个圆柱,下部分是一个长方体,∴其体积为 30×25×40=3200π+30000(cm ),其表面积为S=(30×40 +30×25+40×25)×2+32×20π=5900 +640π(cm ).
21.解:(1)这个几何体的名称是正三棱柱;
(2)表面展开图如图所示:(答案不唯一,画出其中正确的一种即可)
(3)3×3×2=18(cm ).
∴这个几何体的侧面积为18 cm .
22.解:(1)由左侧两个图形可得,与2相邻的面为3,4,5,6,
∴2 的对面是1,即第一个图的下底面为1,又由第一个和第三个图可得,与6相邻的面为2,4,5,
∴第一个图的左面是4,后面为3,
∴结合第一个和第三个图可得“ ”处的点数为2;
(2)由第一个图可知,4的对面是5,
∴第二个图和第三个图的下底面都为5,
∴这三个骰子下底面上的点数和为1+5+5=11.
23.解:(1)如图所示:
(2)3×3×3×10=270(cm ),
答:该物体的体积是270 cm ;
(3)(6+6+6)×3×3×2=324(cm ),
答:该物体的表面积是324 cm .
第二十九章 投影与视图达标测评卷
一、选择题(本题共计10小题,每题3分,共计30分)
1.下列投影现象属于平行投影的是 ( )
A.太阳光发出的光线所形成的投影
B.手电筒发出的光线所形成的投影
C.路灯发出的光线所形成的投影
D.台灯发出的光线所形成的投影
2.下面属于中心投影的是 ( )
A.太阳光下的树影 B.皮影戏—
C.月光下房屋的影子 D.海上日出
3.从早上太阳升起的某一时刻开始到晚上,旭日广场的旗杆在地面上的影子的变化规律是 ( )
A.先变长,后变短 B.先变短,后变长
C.方向改变,长短不变 D.以上都不正确
4.如图,属于“物体在太阳光下形成的影子”的图形是 ( )
5.如图,光线由上向下照射正五棱柱时的正投影是 ( )
6.如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为2:5,且三角板的一边长为8cm .则投影三角板的对应边长为 ( )
A.20 cm B.10 cm C.8 cm D.3. 2cm
7.如图,路灯距地面8米,身高1.6米的小明从距离灯底(点 O)20米的点A处,沿AO所在的直线行走12米到达点B时,小明身影长度 ( )
A.变长2.5米 B.变短2米
C.变短3米 D.变短2.5米
8.两个长方体按如图方式摆放,其主视图是 ( )
9.甲和乙两个几何体都是由大小相同的小立方块搭成,它们从上面看得到的图形如图,小正方形中数字表示该位置上的小立方块个数,则下列说法中正确的是 ( )
A.甲和乙从左面看得到的图相同,从正面看得到的图相同
B.甲和乙从左面看得到的图不相同,从正面看得到的图不相同
C.甲和乙从左面看得到的图相同,从正面看得到的图不相同
D.甲和乙从左面看得到的图不相同,从正面看得到的图相同
10.如图是由 10个棱长为1的小正方体摆成的几何体.将小正方体①移走后,则关于新几何体的表面积表述正确的是 ( )
A.表面积不变 B.表面积减少4
C.表面积减少2 D.表面积增加4
二、填空题(本题共计5 小题,每题3 分,共计15分)
11.如图,王华晚上由路灯A下的B处走到C 处时,测得影子 CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB= 米.
12.从棱长为4的正方体毛坯的一角,挖去一个棱长为2的小正方体,得到一个如图所示的零件,则这个零件的表面积为 .
13.一位美术老师在课堂上进行立体模型素描教学时,把14个棱长为1分米的正方体摆成如图所示的形式,然后把露出的表面涂上不同的颜色,则被涂上颜色部分的面积为 平方分米.
14.如图,是一个长方体的主视图,左视图与俯视图,根据图中数据计算这个长方体的表面积是 .
15.如图是由一些大小相同的小正方体组成的几何体的主视图和俯视图,若组成这个几何体的小正方体的块数为n,则n的最小值为 .
三、解答题(本题共计8 小题,共计75 分)
16.(8分)如图,是由8个完全相同的小正方体堆成的几何体.
(1)设小正方体的棱长为 m,直接写出这个几何体的表面积(含底面);
(2)请画出从这个几何体的三个不同方向看到的形状图.
17.(9分)如图,AB 和 DE是直立在地面上的两根立柱, 某一时刻AB在阳光下的投影
(1)请你画出此时 DE 在阳光下的投影;
(2)在测量AB的投影时,同时测量出 DE 在阳光下的投影长为 请你计算,DE 的长.
18.(9分)如图,身高1.5米的小明(AB)在太阳光下的影子AG长1.8米,此时,立柱CD的影子一部分落在地面CE上,一部分落在墙 EF 上.
(1)请你在墙上画出表示 CD 的部分影子 EH.;
(2)若量得( 米, 米,求立柱CD的高.
19.(10分)如图所示的是一个几何体的三视图.
(1)该几何体是 ;(填几何体的名称)
(2)求出这个几何体的体积.
20.(9 分)如图所示是一个几何体的主视图和俯视图,求该几何体的体积及其表面积(保留 π).
21.(10分)如图,是一个几何体从三个方向看所得到的形状图:
(1)写出这个几何体的名称;
(2)画出它的一种表面展开图;
(3)若从正面看长方形的高为3cm,从上面看三角形的边长为2cm ,求这个几何体的侧面积.
22.(9分)如图是一颗骰子的三种不同的放置方法.
(1)根据图中三种放置方法,推出“ ”处的点数;
(2)求这三个骰子下底面上的点数和.
23.(11 分)一个物体是由棱长为3c m的正方体模型堆砌而成的,其形状从三个方向看如图所示:
(1)请在从上面看到的形状图上标出每个位置中小正方体的个数;
(2)求出该物体的体积是多少;
(3)该物体的表面积是多少
1-10ABBDC ACDDC
11.6.
12.96 【解析】利用平移的方法,从棱长为4的正方体毛坯的一角,挖去一个棱长为2 的小正方体后所得几何体的表面积与原正方体的表面积相同.这个零件的表面积=6×4×4=96.
13.33 【解析】根据分析露出的面积为4×(1+2+3)+9=33(dm ),即涂上颜色的面积为33dm .故答案为33.
14.52
15.8 【解析】根据主视图和俯视图可知,该几何体中小正方体数最少的分布情况如下:
∴n=1+1+2+1+3=8.
故答案为8.
16.解:
(2)如图:
17.解:(1)连接AC,过点 D 作 DF∥AC,则 EF 为所求;
(2)∵AC∥DF,∴ ∠ACB=∠DFE,
又∠ABC=∠DEF=90°,
.. Rt△ABC∽Rt△DEF,
即 解得DE=10,
即 DE 的长为 10 m.
18.解:(1)如图,线段 EH为所求;
(2)过点E作EM∥BG,交CD于点M,则四边形 DHEM 是平行四边形,
即 DM=EH=1.5米,
解得 CM=1,
∴CD=CM+DM=1+1.5=2.5(米),
故立柱 CD 的高为2.5 米.
19.解:(1)由三视图可知该几何体的形状是三棱柱,故答案为三棱柱;
(2)由俯视图可知该三棱柱底面是等腰三角形,由主视图可知底面三角形底边为1+1=2,三棱柱高为2,
由左视图可知底面三角形高为1,故该几何体的体积为
20.解:由主视图和俯视图可知,该几何体是一个组合体,其上部分是一个圆柱,下部分是一个长方体,∴其体积为 30×25×40=3200π+30000(cm ),其表面积为S=(30×40 +30×25+40×25)×2+32×20π=5900 +640π(cm ).
21.解:(1)这个几何体的名称是正三棱柱;
(2)表面展开图如图所示:(答案不唯一,画出其中正确的一种即可)
(3)3×3×2=18(cm ).
∴这个几何体的侧面积为18 cm .
22.解:(1)由左侧两个图形可得,与2相邻的面为3,4,5,6,
∴2 的对面是1,即第一个图的下底面为1,又由第一个和第三个图可得,与6相邻的面为2,4,5,
∴第一个图的左面是4,后面为3,
∴结合第一个和第三个图可得“ ”处的点数为2;
(2)由第一个图可知,4的对面是5,
∴第二个图和第三个图的下底面都为5,
∴这三个骰子下底面上的点数和为1+5+5=11.
23.解:(1)如图所示:
(2)3×3×3×10=270(cm ),
答:该物体的体积是270 cm ;
(3)(6+6+6)×3×3×2=324(cm ),
答:该物体的表面积是324 cm .
