7.1 角与弧度 课件(共110张PPT)
文档属性
| 名称 | 7.1 角与弧度 课件(共110张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 67.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 21:42:33 | ||
图片预览











文档简介
(共110张PPT)
第7章
三角函数
7 . 1
角与弧度
我们已经学习过一些角,如锐角、直角、钝角、平角、周角. 利用这些角,我们已能表示圆周上某些点 P. 但要表示圆周上周而复始地运动着的点,仅有这些角是不够的. 如点 P 绕圆心旋转一周半,所在位置怎样用角来表示
在生活中,也有类似情形. 如“游乐园的摩天轮旋转了两周半”为了精确地刻画旋转程度,我们需要引入一个角,来量化“两周半”.
● 旋转两周半是转了怎样的一个角
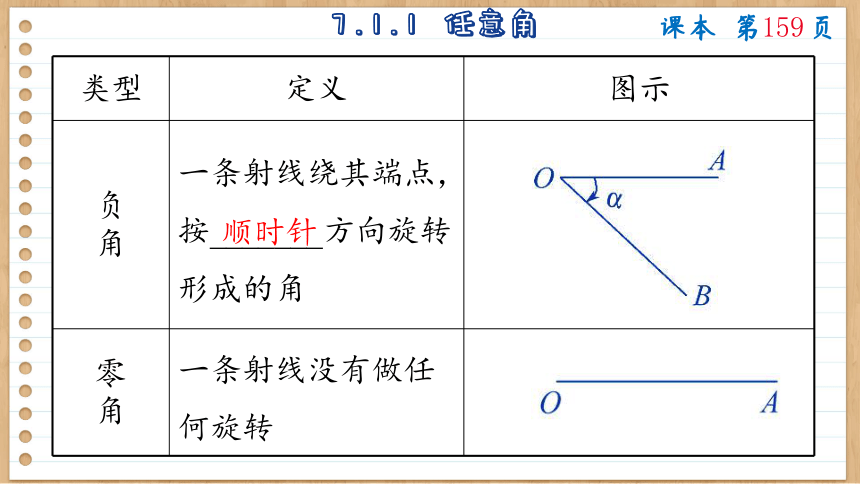
7.1.1 任意角
一个角可以看作平面内一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形.
射线的端点称为角的顶点,射线旋转的开始位置和终止位置称为角的始边和终边.
如图 7-1-1所示,射线 OA 绕端点O,按头所示方向旋转到OB 便形成角α. 点O是角α 的顶点,射线 OA 和 OB 分别是α 的始边和终边.
因此,361°就是旋转一周后紧接
着又旋转了1°所形成的角;720°就
是旋转两周所形成的角;旋转两周半,
就是旋转了 900°的角.
一、任意角
(1) 角的分类
类型 定义 图示
正 角 一条射线绕其端点,按_______方向旋转形成的角
逆时针
类型 定义 图示
负 角 一条射线绕其端点, 按_______方向旋转 形成的角
零 角 一条射线没有做任 何旋转
顺时针
(2) 本质:
将初中所学的锐角、直角、钝角、平角和周角等推广到任意角.
例如图中的 α=420°,β=-150°.
(3) 应用:可以定义任意的旋转角.
对于两个任意角 α,β,将角 α 的终边旋转角β (当β是正角时,按逆时针方向旋转;当β是负角时,按顺时针方向旋转;当 β是零角时不旋转),这时终边所对应的角称为α与β的和,记作 α+β. 射线 OA绕端点O 分别按逆时针方向、顺时针方向旋转相同的量所成的两个角称为互为相反角.角 α 的相反角记为-α,于是有
α-β=α+(-β).
二、象限角
角的顶点为坐标原点,角的始边为x轴_______,建立平面直角坐标系,这样,角的终边(除端点外) 在第几象限,就说这个角是______________.如果角的终边在坐标轴上,称这个角为轴线角.
正半轴
第几象限角
思 考
(1) -300°,-150°,-60°,60°,210°,300°,420°角分别是第几象限角 其中哪些角的终边相同
(2) 具有相同终边的角彼此之间有什
么关系 你能写出与 60°角终边相同
的角的集合吗 (图 7-1-4)
三、终边相同的角
(1) 定义:所有与角 α 终边相同的角,连同角 α 在内.
(2) 表示:集合 S={β∣β=α+k·360°,k∈Z}.
(3) 本质:表示成角 α 与整数个周角的和.
【思考】
反过来,若角α,β满足S={β∣β=α+k·360°,k∈Z}
时,角α,β是否是终边相同的角
提示:当角 α,β 满足S={β∣β=α+k·360°,k∈Z}时,表示角α与β相隔整数个周角,即角 α,β 终边相同.
例 1
在0°到 360°的范围内,找出与下列各角终边相同的角,并分别判断它们是第几象限角:
(1) 650°; (2) -150°; (3) -990°15′.
分析 只需将这些角表示成 k·360°+α (0°<α<360°)的形式,然后根据 α 来确定它们所在的象限.
(1) 650°;
(2) -150°;
解 因为650°=360°+290°,
所以 650°的角与 290°的角终边相同,是第四象限角.
解 因为-150°=-360°+210°,
所以-150°的角与210°的角终边相同,是第三象限角.
(3) -990°15′.
解 因为-990°15′=-3×360°+89°45′,
所以-990°15′的角与 89°45′的角终边相同,
是第一象限角.
例 2
已知 α 与 240°角的终边相同,判断 是第几象限角.
解 由 α= k·360°+240°(k∈Z),可得
= k.180° + 120°(k∈Z).
若k为偶数,设 k=2n,n∈Z,则
= n.360° +120°(n∈Z).
若k为奇数,设 k=2n+1,n∈Z,则
= n.360° +300°(n∈Z),
从而与 300°角的终边相同,是第四象限角.
因此, 是第二或第四象限角.
思 考
(1) 终边落在x轴正半轴上的角的集合如何表示 终边落在 x轴上的角的集合如何表示
(2) 终边落在坐标轴上的角的集合如何表示
(3) 若α是第三象限角,则一是第几象限角
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 经过1小时,时针转过30°. ( )
(2) 终边与始边重合的角是零角. ( )
(3) 第二象限的角是钝角. ( )
2. 与 45°角终边相同的角是 ( )
A. -45° B. 225° C. 395° D. -315°
D
解析:与45°角终边相同的角可以表示为 45°+k·360°,
k∈Z,结合四个选项可以发现只有答案D符合题意.
解析
3. 已知 0°≤α<360°,且 α 与600°角终边相同,则
α=______,它是第______象限角.
240°
三
解析:因为600°=360°+240°,所以240°角与600°角终边相同,且0°≤240°<360°,故α=240°,它是第三象限角.
解析
【跟踪训练】
1. 在下列说法中,正确的是 ( )
①时钟经过两个小时,时针转过的角是60°;
② 钝角一定大于锐角;
③ 射线OA绕端点O按逆时针旋转一周所成的角是0°;
④ - 2 000°是第二象限角.
A.①② B.③④ C.①③ D.②④
D
2. 179°角是 ( )
A. 第一象限角 B.第二象限角
C. 第三象限角 D.第四象限角
B
解析:179°是第二象限角.
解析
3.与-457°角终边相同的角的集合是 ( )
A.{α|α=k·360°+457°,k∈Z}
B.{α|α=k·360°+97°,k∈Z}
C.{α|α=k·360°+263°,k∈Z}
D.{α|α=k·360°-263°,k∈Z}
C
解析:-457°=-2×360°+263°,所以与-457°角终边相同的角的集合是{α|α=k·360°+263°,k∈Z}.
解析
4. 若角α=m·360°+60°,β=k·360°+120°(m,k∈Z),则角α与β的终边的位置关系是 ( )
A.重合 B.关于原点对称
C.关于x轴对称 D.关于y轴对称
D
解析:角α的终边和60°角的终边相同,角β的终边与120°角终边相同,因为180°-120°=60°,所以角α与β的终边的位置关系是关于y轴对称.
解析
5. 2 021°角是第________象限角.
三
解析:因为2 021°=5×360°+221°,因为221°角在第三象限,所以2 021°是第三象限角.
解析
练 习
1. (口答) 写出 3 个与 60°角终边相同的角:
___________________________.
420°;780°;1140°
2. (口答)下列角中哪些角与 30°角的终边相同:
(1) 210°;(2) -330°;
解 (1) 210°-30°=180°,所以210°与30角的终边不相同.
(2) -330°-30°=-360°,所以-330°与30°角的终边相同.
(3) 390°; (4) 750°.
(3) 390°- 30°=360°,所以390°与30°角的终边相同.
(4) 750°-30°=720°=360°×2,所以750°与30°角的终边相同.
3. 分别写出满足下面条件的角的集合:
(1) 终边为 y 轴负轴;
解 终边落在 y 轴负半轴的角的集合可表示为:{x∣x=-+2kπ,k∈Z}.
(2) 终边落在坐标轴上.
解 终边在x轴上的角的集合为{α∣α=kπ,k∈Z},
终边在y轴上的角的集合为{α∣α=kπ+,k∈Z},
故终边在坐标轴上的角的集合为
{α∣α =,n∈Z}.
4. 分别作出下列各角的终边,并指出它们是第几象限角:
(1) 330°;
解 330°-360° = -30°,是第四象限角,
如图:
(2) -200°;
解 -200°+360°=160°,是第二象限角,
如图:
(3) 945°;
解 945°-360°×3=-135°,是第三象限角,
如图:
(4) -650°.
解 -650°+360°×2=70°,是第一象限角,
如图:
5. 在0°到360°的范围内,找出与下列各角终边相同的角,并判断它们是第几象限角:
(1) -55°;
解 -55°=305°- 360°,
270° < 305° < 360°,
∴在0°到360°的范围内与该角终边相同的角为305°,且为第四象限.
(2) 395°8′;
解 ∵ 395°8′=35°8′ +360°,
0°< 35°8′<90°,
∴ 在0°到360°的范围内与该角终边相同的角为35°8′,且为第一象限.
(3) 1 563°.
解 ∵ 1563°=123°+4×360°,
90°< 123°<180°,
∴ 在0°到360°的范围内与该角终边相同的角为123°,且为第二象限.
6.下列命题中正确的是 ( ).
A. 第一象限角一定不是负角
B. 小于 90°的角一定是锐角
C. 钝角一定是第二象限角
D. 第一象限角一定是锐角
C
7. 求出与下列各角终边相同的最小正角和最大负角:
(1) 1 140°;
解 与1140°终边相同的角可表示为:
{α∣α= k·360°+60°,k∈Z}.
则当k=-1时, α=-1×360°+60°=-300°,
此时为最大的负角,
当 k=0 时, α=0×360°+60°=60°,此时为最小的正角.
(2)1 680;
解 与1680°终边相同的角可表示为:
{α∣α = k·360° + 240°,k∈Z}.
则当k=-1时, α=-1×360°+240°=-120°, 此时为最大的负角.
当 k=0 时, α=0×360°+240°=240°,此时为最小的正角.
(3) -1290°;
解 与-1290°终边相同的角可表示为
{α∣α=k·360° -210°,k∈Z}.
则当k=0时,α=0×360°-210°=-210°,
此时为最大的负角.
当k=1时, α=1×360°-210°=150°,此时为最小的正角.
(4) -1 510°.
解 与-1510°终边相同的角可表示为
{α∣α = k·360°- 70°,k∈Z}.
则当k=0时, α=0×360°-70°=-70°,此时为最大的负角.
当k=1时, α=1×360°-70°=290°,此时为最小的正角.
8. 已知 α 是第四象限角,分别确定-α ,180° +α ,
180°-α 是第几象限角.
解 ∵ α 是第四象限角,
∴ k·360°-90°< α < k·360°,k∈Z,
∴ -k·360°<-α <-k·360°+90°,k∈Z,
故-α 是第一象限角;
k·360°+ 90°<α+180°<k·360+180°,k∈Z,
故 180°+α 是第二象限角;
-k·360°+180°<180°-α < k·360+270°,k∈Z,故 180°-α 是第三象限角.
7.1.2 弧度制
在本章引言中,我们曾考虑用有序数对 (r,α) 或 (r,l) 来表示点P,那么,
● r,l 与 α 之间具有怎样的关系呢
一、角度制
我们已学习过角的度量,规定周角的 为 1 度的角,这种用度作为单位来度量角的单位制叫作角度制.
二、弧度制
(1) 弧度制
①1弧度的角:长度等于__________的弧所对的圆心角叫做1弧度的角.
②表示方法:1弧度记作1 rad.
半径长
上述规定基于下面的基本事实:
假设角 α 作为圆心角所在的圆有两个,其半径分别为r1,r2,所对应的弧长分别为l1,l2(图 7-1- 6),
则 =.
上式表明,角 α 的弧度数由角 α 的大小唯一确定,而与其为圆心角所在圆的大小(半径)无关.
这种用弧度作为角的单位来度量角的单位制称为弧度制.
正角的弧度数是正数,负角的弧度数是负数,零角的弧度数为0.
(2) 角的弧度数的计算
在半径为r的圆中,弧长为l的弧所对的圆心角为α rad,那么,|α|=___.
(3) 本质:
角的两种不同的度量模式,适用情况不同,而且弧度是表示角的默认单位.
(4) 应用:
角度制更容易理解和运算,与小学、初中知识更容易衔接;
弧度制表示角应用更广泛,与实数一一对应.
【思考】
初中学习的角度制是怎样定义的 1°角是多少
提示:定义:用度为单位来度量角的单位制;
1度的角:周角的 为1度角,记作1°.
三、角度制与弧度制的换算
角度化弧度 弧度化角度
360°=____ rad 2π rad=______
180°=___ rad π rad= ______
1°=rad≈0.017 45 rad 1 rad=()°≈57.30°
度数×=弧度数 弧度数×()°=度数
2π
360°
π
180°
图 7-1-9 给出了一些角的弧度数与角度数之间的关系.
用弧度表示角的大小时,只要不引起误解,可以省略单位. 例如l rad,2 rad,π rad,可分别写成 1,2,π.
【思考】
角度制、弧度制都是角的度量制,那么它们之间换算的关键是什么
提示:计算时,我们要特别注意 π rad = 180°,用这个公式进行互化即可.
例 3
把下列各角从弧度化为度:
(1) ; (2) 3.5.
解:(1) rad = × = 108°.
(2) 3.5 rad = 3.5×≈ 200.54°
例 4
把下列各角从度化为弧度:
(1) 252°; (2) 11°15′.
解: (1) 252°= 252× rad = rad.
(2) 11°15′=11. 25°=11. 25×rad=rad.
如图 7-1-10,设长度为 r 的线段 OA 绕端点 O 旋转形成角 α ( α 为任意角,单位为弧度).
四、扇形的弧长和面积公式
设扇形的半径为R,弧长为l,α 为其圆心角,则
(1) 弧长公式:l=____.
(2) 扇形面积公式:S=_____=______.
lR
αR2
αR
【思考】
初中学过的半径为r,圆心角为n°的扇形弧长、面积公式分别是什么
提示:半径为r,圆心角为n°的扇形弧长公式为l=,扇形面积公式为 S扇= .
例 5
已知扇形的周长为 8 cm,圆心角为 2 rad,求该扇形的面积.
解 设扇形的半径为r,弧长为 l,则有
2r+l=8, r=2,
解得
l=2r, l=4.
故扇形的面积为 S=rl=4 (cm2).
引入弧度制后,在∣θ∣=中,不妨取 r=l (这时的圆也称单位圆),那么当θ为正角时, θ 的弧度数即为其所对应的弧长l的数量;当θ为负角时, θ 的弧度数即为其所对应的弧长 l 的数量的相反数;当 θ 为零角时, θ 的弧度数为 0 .
角的概念推广以后,在弧度制下,角的集合与弧度数的集合之间建立起一一对应关系,即角的集合与实数集 R 之间建立起一一对应关系:每一个角都对应唯一的一个实数;反过来,每一个实数也都对应唯一的一个角.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 1弧度就是1°的圆心角所对的弧. ( )
(2)“1弧度的角”的大小和所在圆的半径大小有关.
( )
(3) 1弧度的角是周角的 . ( )
2. 将角1 080°化为弧度制等于 ( )
A. 1 080 B. C. D. 6π
D
解析:1 080°= 180°×6,所以1 080°化为弧度制是6π.
解析
3. 半径为2,圆心角为 的扇形的面积是________.
解析:由已知得 S扇=× ×22= .
解析
【跟踪训练】
1.下列说法中,错误的是 ( )
A.半圆弧所对的圆心角是π rad
B.周角的大小等于2π
C.1弧度的圆心角所对的弧长等于该圆的半径
D.长度等于半径的弦所对的圆心角的大小是1弧度
D
解析:根据弧度的定义及角度与弧度的换算知A,B,C 均正确,D错误.
解析
2. 1 920°的角化为弧度数为 ( )
A. rad B. rad
C. π rad D. π rad
D
解析:因为1°= rad,
所以1 920°=1 920×= π rad.
解析
3. 时钟的分针在1点到3点20分这段时间里转过的弧度为 ( )
A. π B. -π C. π D. -π
B
解析:显然分针在1点到3点20分这段时间里,顺时针转过了周,转过的弧度为-×2π =-π.
解析
4. 若某扇形的弧长为,圆心角为,则该扇形的半径是 ( )
A. B. C.1 D.2
D
解析:设扇形的半径为r,因为扇形的弧长为,圆心角为,所以由扇形的弧长公式可得:= ×r,解得r=2.
解析
解析:150°=150×=,半径 R=10 cm,
所以 l=αR=×10= (cm).
5. 在直径为20 cm的圆中,150°的圆心角所对的弧长为________.
解析
练 习
1. (口答) 把下列各角从度化为弧度:
(1) 180°; (2) 90°; (3) 45°;
(1) 180°=π;
(2) 90° =90 × =;
(3) 45° =45 × =;
(4) 30°; (5) 120°; (6) 270°.
(4) 30°=30× =;
(5) 120°=120 ×=;
(6) 270° =270 × =;
2. (口答) 把下列各角从弧度化为度:
(1) 2π; (2) ; (3) ; (4) π.
(1) 2π= 2π × =360°;
(2) = ×=90°;
(3) = ×=30°;
(4) =×=120°;
3. 把下列各角从度化为弧度:
(1) 75°;(2) -210°; (3) 135°; (4) 22°30′.
(1) 75°=75× =;
(2) -210°=-210×=-;
(3) 135°=135× =;
(4) 22°30′=22.5°=22.5× =;
4. 把下列各角从弧度化为度:
(1) ; (2) π; (3) -π; (4) -12π.
(1) =× =15°;
(2) = ×=72°;
(3) -=-×=-240°;
(4) -12π=-12π×= - 2160°.
5. 写出与下面的角终边相同的角的集合:
(1) ; (2) .
解 (1) 与终边相同的角的集合为:
{α∣α =2kπ+,k∈Z};
(2) 与终边相同的角的集合为:
{α∣α =2kπ+,k∈Z}.
6. 分别用弧度制表示下列角的集合:
(1) 终边落在 x 轴上的角;
(2) 终边落在 y 轴上的角.
解 (1) 终边落在x轴上的角: {α∣α=kπ,k ∈Z}.
(2) 终边落在y轴上的角: {α∣α=kπ+ ,k ∈Z}.
7. 若 α=-6,则角 α 的终边在 ( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限
A
8. 已知半径为 240 mm的圆上,有一段弧的长是 500 mm,
求此弧所对的圆心角的弧度数.
解 首先设该弧所对的圆心角的度数为α ,代入弧长计算公式可得 240α = 500,然后可求得 α = rad.
习题 7.1
感受·理解
1. 在0°到 360°范内,找出与下列各角终相同的角,
并指出它们是第几象限角:
(1) -265°; (2) 3 900°;
(3) -840°10′; (4) 560°24′.
(1) -265°;
(2) 3 900°;
解 ∵-265°=-360°+95°,95°是第二象限的角,
∴-265°是第二象限的角;
解 ∵3900°=3600°+300°,300°是第四象限的角,
∴3900°是第四象限的角;
(3) -840°10′;
(4) 560°24′.
解 ∵-840°10′=-1080°+239°50′,
239°50′是第三象限的角,
∴ -840°10′是第三象限的角;
解 ∵560°24′=360°+200°24′,
200°24′是第三象限的角,
∴ 560°24′是第三象限的角;
2. 分别写出与下列各角终边相同的角的集合,并把集合
中适合 -360°≤α≤360°的元素α写出来:
(1) 60°;
(2) -75°;
解 由题意可知: A={x∣x = k·360°+60°,k∈Z},
当k=0, -1时, α=60°, -300°.
解 由题意可知: B={x∣x = k·360°-75°,k∈Z},
当k=0, 1时, α=-75°, 285°.
(3) 90°;
(4) -180°.
解 由题意可知: C={x∣x = k·360°+90°,k∈Z},
当k=0, -1时, α=90°, -270°.
解 由题意可知: D={x∣x =k·360°-180°,k∈Z},
当k=0, 1时, α=-180°, 180°.
3. 分别把下列各角从度化为弧度:
(1) 12°30′;
(2) -200°;
解 12°30′ = 12.5°=·π =;
解 -200°=·π = - ;
(3) 355°;
(4) -186°45′.
解 355°=·π =;
解 -186°45′=-186.75°=·π =-;
4. 分别把下列各角从弧度化为度:
(1)-; (2) ; (3) ; (4) 1.4.
解 (1) - ·=-75°;
(2) =480°;
(3) = · = ;
(4) 1.4=1.4· = .
5. 终边落在直线 y=x 上的角的集合如何表示
解 终边落在直线 y=x 上的角的集合为与 , 同终边的角组成的集合,
与同终边的角可表示为: +2kπ,k∈Z,
与同终边的角可表示为: +2kπ= +π+2kπ = +(2k+1)π ,k∈Z,
所以终边落在直线y=x上的角的集合为{α|α=+kπ,k∈Z}.
6. 把下列各角化成 α+2kπ (0≤α<2,k∈Z)的形式,并
分别指出它们是第几象限角:
(1) ; (2) -1500°;
(1) =2π+,是第四象限角.
(2) -1500°= -1800°+300°= -10π+,是第四象限角.
(3) -=-4π+,是第三象限角;
(4) 672°=360°+312°=2π+,是第四象限角;
(3) -; (4) 672°.
7. 如果 α 与120°角终边相同,那么是第几象限角
解 ∵ α与120°终边相同,
∴ α=120°+k·360°(k∈Z),
∴ =60°+k·180°(k∈Z),
当k=2n(n∈Z)时, 为第一象限角,
当 k=2n+1 (n∈Z) 时,
=60°+(2n+1)·180°= 240°+n·360°,
为第三象限角.
∴ 为第一或第三象限角.
8. 已知扇形的半径为 10 cm,圆心角为 60°,求扇形的
弧长和面积.
解 ∵扇形的半径 r=10,圆心角α=60°=,
∴弧长:l=rα=10×= (cm).
面积:S=lr =××10= (cm2).
9. 蒸汽机飞轮的直径为 1.2 m,以300 r/min(转/分)的速度
作逆时针旋转,求:
(1)飞轮1s 内转过的弧度数;
解 ∵ 飞轮转速 300 r/min (转/分) = 5r/s (转/秒),
而且飞轮作逆时针旋转,
∴ 它每 1s 转过的弧度数为 5×2π=10π.
(2) 轮周上一点 1s 内所经过的路程.
解 轮上一点每 1s 所转过的弧长为:
L= αr = 10π×0.6 =6π米
思考·运用
10. 已知 α=,角 β 的终边与角 α 的终边关于直线 y=x
对称,求 β 的集合.
解 当 β∈[0,2π) 时,
∵∠α=,且角β的终边与∠α 的终边关于直线 y=x 对称,可得β=,
故当β∈R时,角β的取值集合是{β|β =+2kπ, k∈Z}.
11. 如图,写出终边落在阴影部分的角的集合(包括边界).
根据边界来确定角的集合,得:{θ∣kπ+≤θ≤kπ+ k∈Z}
根据边界来确定角的集合,得:{θ∣2kπ-≤θ≤2kπ+ k∈Z}
探究·拓展
12. 设 θ 是第一象限角,试探究:
(1) 2θ 一定不是第几象限角
解 ∵ θ是第一象限角,
∴ 2kπ <θ<2kπ+,k∈Z;
∴ 4kπ<2θ<4kπ+π, k∈Z;
∴ 2θ不是第三、四象限角;
(2) 是第几象限角
解 ∵2kπ<θ<2kπ+,k∈Z;
∴ <<+,k∈Z;
∴ k=0时,0<<,是第一象限角;
k=1时, <<,是第二象限角;
k=2时, <<,是第二象限角;
k=3时, <<,是第一象限角;
综上, 是第一、二、三象限角.
本课结束
This lesson is over
THANKS!
第7章
三角函数
7 . 1
角与弧度
我们已经学习过一些角,如锐角、直角、钝角、平角、周角. 利用这些角,我们已能表示圆周上某些点 P. 但要表示圆周上周而复始地运动着的点,仅有这些角是不够的. 如点 P 绕圆心旋转一周半,所在位置怎样用角来表示
在生活中,也有类似情形. 如“游乐园的摩天轮旋转了两周半”为了精确地刻画旋转程度,我们需要引入一个角,来量化“两周半”.
● 旋转两周半是转了怎样的一个角
7.1.1 任意角
一个角可以看作平面内一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形.
射线的端点称为角的顶点,射线旋转的开始位置和终止位置称为角的始边和终边.
如图 7-1-1所示,射线 OA 绕端点O,按头所示方向旋转到OB 便形成角α. 点O是角α 的顶点,射线 OA 和 OB 分别是α 的始边和终边.
因此,361°就是旋转一周后紧接
着又旋转了1°所形成的角;720°就
是旋转两周所形成的角;旋转两周半,
就是旋转了 900°的角.
一、任意角
(1) 角的分类
类型 定义 图示
正 角 一条射线绕其端点,按_______方向旋转形成的角
逆时针
类型 定义 图示
负 角 一条射线绕其端点, 按_______方向旋转 形成的角
零 角 一条射线没有做任 何旋转
顺时针
(2) 本质:
将初中所学的锐角、直角、钝角、平角和周角等推广到任意角.
例如图中的 α=420°,β=-150°.
(3) 应用:可以定义任意的旋转角.
对于两个任意角 α,β,将角 α 的终边旋转角β (当β是正角时,按逆时针方向旋转;当β是负角时,按顺时针方向旋转;当 β是零角时不旋转),这时终边所对应的角称为α与β的和,记作 α+β. 射线 OA绕端点O 分别按逆时针方向、顺时针方向旋转相同的量所成的两个角称为互为相反角.角 α 的相反角记为-α,于是有
α-β=α+(-β).
二、象限角
角的顶点为坐标原点,角的始边为x轴_______,建立平面直角坐标系,这样,角的终边(除端点外) 在第几象限,就说这个角是______________.如果角的终边在坐标轴上,称这个角为轴线角.
正半轴
第几象限角
思 考
(1) -300°,-150°,-60°,60°,210°,300°,420°角分别是第几象限角 其中哪些角的终边相同
(2) 具有相同终边的角彼此之间有什
么关系 你能写出与 60°角终边相同
的角的集合吗 (图 7-1-4)
三、终边相同的角
(1) 定义:所有与角 α 终边相同的角,连同角 α 在内.
(2) 表示:集合 S={β∣β=α+k·360°,k∈Z}.
(3) 本质:表示成角 α 与整数个周角的和.
【思考】
反过来,若角α,β满足S={β∣β=α+k·360°,k∈Z}
时,角α,β是否是终边相同的角
提示:当角 α,β 满足S={β∣β=α+k·360°,k∈Z}时,表示角α与β相隔整数个周角,即角 α,β 终边相同.
例 1
在0°到 360°的范围内,找出与下列各角终边相同的角,并分别判断它们是第几象限角:
(1) 650°; (2) -150°; (3) -990°15′.
分析 只需将这些角表示成 k·360°+α (0°<α<360°)的形式,然后根据 α 来确定它们所在的象限.
(1) 650°;
(2) -150°;
解 因为650°=360°+290°,
所以 650°的角与 290°的角终边相同,是第四象限角.
解 因为-150°=-360°+210°,
所以-150°的角与210°的角终边相同,是第三象限角.
(3) -990°15′.
解 因为-990°15′=-3×360°+89°45′,
所以-990°15′的角与 89°45′的角终边相同,
是第一象限角.
例 2
已知 α 与 240°角的终边相同,判断 是第几象限角.
解 由 α= k·360°+240°(k∈Z),可得
= k.180° + 120°(k∈Z).
若k为偶数,设 k=2n,n∈Z,则
= n.360° +120°(n∈Z).
若k为奇数,设 k=2n+1,n∈Z,则
= n.360° +300°(n∈Z),
从而与 300°角的终边相同,是第四象限角.
因此, 是第二或第四象限角.
思 考
(1) 终边落在x轴正半轴上的角的集合如何表示 终边落在 x轴上的角的集合如何表示
(2) 终边落在坐标轴上的角的集合如何表示
(3) 若α是第三象限角,则一是第几象限角
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 经过1小时,时针转过30°. ( )
(2) 终边与始边重合的角是零角. ( )
(3) 第二象限的角是钝角. ( )
2. 与 45°角终边相同的角是 ( )
A. -45° B. 225° C. 395° D. -315°
D
解析:与45°角终边相同的角可以表示为 45°+k·360°,
k∈Z,结合四个选项可以发现只有答案D符合题意.
解析
3. 已知 0°≤α<360°,且 α 与600°角终边相同,则
α=______,它是第______象限角.
240°
三
解析:因为600°=360°+240°,所以240°角与600°角终边相同,且0°≤240°<360°,故α=240°,它是第三象限角.
解析
【跟踪训练】
1. 在下列说法中,正确的是 ( )
①时钟经过两个小时,时针转过的角是60°;
② 钝角一定大于锐角;
③ 射线OA绕端点O按逆时针旋转一周所成的角是0°;
④ - 2 000°是第二象限角.
A.①② B.③④ C.①③ D.②④
D
2. 179°角是 ( )
A. 第一象限角 B.第二象限角
C. 第三象限角 D.第四象限角
B
解析:179°是第二象限角.
解析
3.与-457°角终边相同的角的集合是 ( )
A.{α|α=k·360°+457°,k∈Z}
B.{α|α=k·360°+97°,k∈Z}
C.{α|α=k·360°+263°,k∈Z}
D.{α|α=k·360°-263°,k∈Z}
C
解析:-457°=-2×360°+263°,所以与-457°角终边相同的角的集合是{α|α=k·360°+263°,k∈Z}.
解析
4. 若角α=m·360°+60°,β=k·360°+120°(m,k∈Z),则角α与β的终边的位置关系是 ( )
A.重合 B.关于原点对称
C.关于x轴对称 D.关于y轴对称
D
解析:角α的终边和60°角的终边相同,角β的终边与120°角终边相同,因为180°-120°=60°,所以角α与β的终边的位置关系是关于y轴对称.
解析
5. 2 021°角是第________象限角.
三
解析:因为2 021°=5×360°+221°,因为221°角在第三象限,所以2 021°是第三象限角.
解析
练 习
1. (口答) 写出 3 个与 60°角终边相同的角:
___________________________.
420°;780°;1140°
2. (口答)下列角中哪些角与 30°角的终边相同:
(1) 210°;(2) -330°;
解 (1) 210°-30°=180°,所以210°与30角的终边不相同.
(2) -330°-30°=-360°,所以-330°与30°角的终边相同.
(3) 390°; (4) 750°.
(3) 390°- 30°=360°,所以390°与30°角的终边相同.
(4) 750°-30°=720°=360°×2,所以750°与30°角的终边相同.
3. 分别写出满足下面条件的角的集合:
(1) 终边为 y 轴负轴;
解 终边落在 y 轴负半轴的角的集合可表示为:{x∣x=-+2kπ,k∈Z}.
(2) 终边落在坐标轴上.
解 终边在x轴上的角的集合为{α∣α=kπ,k∈Z},
终边在y轴上的角的集合为{α∣α=kπ+,k∈Z},
故终边在坐标轴上的角的集合为
{α∣α =,n∈Z}.
4. 分别作出下列各角的终边,并指出它们是第几象限角:
(1) 330°;
解 330°-360° = -30°,是第四象限角,
如图:
(2) -200°;
解 -200°+360°=160°,是第二象限角,
如图:
(3) 945°;
解 945°-360°×3=-135°,是第三象限角,
如图:
(4) -650°.
解 -650°+360°×2=70°,是第一象限角,
如图:
5. 在0°到360°的范围内,找出与下列各角终边相同的角,并判断它们是第几象限角:
(1) -55°;
解 -55°=305°- 360°,
270° < 305° < 360°,
∴在0°到360°的范围内与该角终边相同的角为305°,且为第四象限.
(2) 395°8′;
解 ∵ 395°8′=35°8′ +360°,
0°< 35°8′<90°,
∴ 在0°到360°的范围内与该角终边相同的角为35°8′,且为第一象限.
(3) 1 563°.
解 ∵ 1563°=123°+4×360°,
90°< 123°<180°,
∴ 在0°到360°的范围内与该角终边相同的角为123°,且为第二象限.
6.下列命题中正确的是 ( ).
A. 第一象限角一定不是负角
B. 小于 90°的角一定是锐角
C. 钝角一定是第二象限角
D. 第一象限角一定是锐角
C
7. 求出与下列各角终边相同的最小正角和最大负角:
(1) 1 140°;
解 与1140°终边相同的角可表示为:
{α∣α= k·360°+60°,k∈Z}.
则当k=-1时, α=-1×360°+60°=-300°,
此时为最大的负角,
当 k=0 时, α=0×360°+60°=60°,此时为最小的正角.
(2)1 680;
解 与1680°终边相同的角可表示为:
{α∣α = k·360° + 240°,k∈Z}.
则当k=-1时, α=-1×360°+240°=-120°, 此时为最大的负角.
当 k=0 时, α=0×360°+240°=240°,此时为最小的正角.
(3) -1290°;
解 与-1290°终边相同的角可表示为
{α∣α=k·360° -210°,k∈Z}.
则当k=0时,α=0×360°-210°=-210°,
此时为最大的负角.
当k=1时, α=1×360°-210°=150°,此时为最小的正角.
(4) -1 510°.
解 与-1510°终边相同的角可表示为
{α∣α = k·360°- 70°,k∈Z}.
则当k=0时, α=0×360°-70°=-70°,此时为最大的负角.
当k=1时, α=1×360°-70°=290°,此时为最小的正角.
8. 已知 α 是第四象限角,分别确定-α ,180° +α ,
180°-α 是第几象限角.
解 ∵ α 是第四象限角,
∴ k·360°-90°< α < k·360°,k∈Z,
∴ -k·360°<-α <-k·360°+90°,k∈Z,
故-α 是第一象限角;
k·360°+ 90°<α+180°<k·360+180°,k∈Z,
故 180°+α 是第二象限角;
-k·360°+180°<180°-α < k·360+270°,k∈Z,故 180°-α 是第三象限角.
7.1.2 弧度制
在本章引言中,我们曾考虑用有序数对 (r,α) 或 (r,l) 来表示点P,那么,
● r,l 与 α 之间具有怎样的关系呢
一、角度制
我们已学习过角的度量,规定周角的 为 1 度的角,这种用度作为单位来度量角的单位制叫作角度制.
二、弧度制
(1) 弧度制
①1弧度的角:长度等于__________的弧所对的圆心角叫做1弧度的角.
②表示方法:1弧度记作1 rad.
半径长
上述规定基于下面的基本事实:
假设角 α 作为圆心角所在的圆有两个,其半径分别为r1,r2,所对应的弧长分别为l1,l2(图 7-1- 6),
则 =.
上式表明,角 α 的弧度数由角 α 的大小唯一确定,而与其为圆心角所在圆的大小(半径)无关.
这种用弧度作为角的单位来度量角的单位制称为弧度制.
正角的弧度数是正数,负角的弧度数是负数,零角的弧度数为0.
(2) 角的弧度数的计算
在半径为r的圆中,弧长为l的弧所对的圆心角为α rad,那么,|α|=___.
(3) 本质:
角的两种不同的度量模式,适用情况不同,而且弧度是表示角的默认单位.
(4) 应用:
角度制更容易理解和运算,与小学、初中知识更容易衔接;
弧度制表示角应用更广泛,与实数一一对应.
【思考】
初中学习的角度制是怎样定义的 1°角是多少
提示:定义:用度为单位来度量角的单位制;
1度的角:周角的 为1度角,记作1°.
三、角度制与弧度制的换算
角度化弧度 弧度化角度
360°=____ rad 2π rad=______
180°=___ rad π rad= ______
1°=rad≈0.017 45 rad 1 rad=()°≈57.30°
度数×=弧度数 弧度数×()°=度数
2π
360°
π
180°
图 7-1-9 给出了一些角的弧度数与角度数之间的关系.
用弧度表示角的大小时,只要不引起误解,可以省略单位. 例如l rad,2 rad,π rad,可分别写成 1,2,π.
【思考】
角度制、弧度制都是角的度量制,那么它们之间换算的关键是什么
提示:计算时,我们要特别注意 π rad = 180°,用这个公式进行互化即可.
例 3
把下列各角从弧度化为度:
(1) ; (2) 3.5.
解:(1) rad = × = 108°.
(2) 3.5 rad = 3.5×≈ 200.54°
例 4
把下列各角从度化为弧度:
(1) 252°; (2) 11°15′.
解: (1) 252°= 252× rad = rad.
(2) 11°15′=11. 25°=11. 25×rad=rad.
如图 7-1-10,设长度为 r 的线段 OA 绕端点 O 旋转形成角 α ( α 为任意角,单位为弧度).
四、扇形的弧长和面积公式
设扇形的半径为R,弧长为l,α 为其圆心角,则
(1) 弧长公式:l=____.
(2) 扇形面积公式:S=_____=______.
lR
αR2
αR
【思考】
初中学过的半径为r,圆心角为n°的扇形弧长、面积公式分别是什么
提示:半径为r,圆心角为n°的扇形弧长公式为l=,扇形面积公式为 S扇= .
例 5
已知扇形的周长为 8 cm,圆心角为 2 rad,求该扇形的面积.
解 设扇形的半径为r,弧长为 l,则有
2r+l=8, r=2,
解得
l=2r, l=4.
故扇形的面积为 S=rl=4 (cm2).
引入弧度制后,在∣θ∣=中,不妨取 r=l (这时的圆也称单位圆),那么当θ为正角时, θ 的弧度数即为其所对应的弧长l的数量;当θ为负角时, θ 的弧度数即为其所对应的弧长 l 的数量的相反数;当 θ 为零角时, θ 的弧度数为 0 .
角的概念推广以后,在弧度制下,角的集合与弧度数的集合之间建立起一一对应关系,即角的集合与实数集 R 之间建立起一一对应关系:每一个角都对应唯一的一个实数;反过来,每一个实数也都对应唯一的一个角.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 1弧度就是1°的圆心角所对的弧. ( )
(2)“1弧度的角”的大小和所在圆的半径大小有关.
( )
(3) 1弧度的角是周角的 . ( )
2. 将角1 080°化为弧度制等于 ( )
A. 1 080 B. C. D. 6π
D
解析:1 080°= 180°×6,所以1 080°化为弧度制是6π.
解析
3. 半径为2,圆心角为 的扇形的面积是________.
解析:由已知得 S扇=× ×22= .
解析
【跟踪训练】
1.下列说法中,错误的是 ( )
A.半圆弧所对的圆心角是π rad
B.周角的大小等于2π
C.1弧度的圆心角所对的弧长等于该圆的半径
D.长度等于半径的弦所对的圆心角的大小是1弧度
D
解析:根据弧度的定义及角度与弧度的换算知A,B,C 均正确,D错误.
解析
2. 1 920°的角化为弧度数为 ( )
A. rad B. rad
C. π rad D. π rad
D
解析:因为1°= rad,
所以1 920°=1 920×= π rad.
解析
3. 时钟的分针在1点到3点20分这段时间里转过的弧度为 ( )
A. π B. -π C. π D. -π
B
解析:显然分针在1点到3点20分这段时间里,顺时针转过了周,转过的弧度为-×2π =-π.
解析
4. 若某扇形的弧长为,圆心角为,则该扇形的半径是 ( )
A. B. C.1 D.2
D
解析:设扇形的半径为r,因为扇形的弧长为,圆心角为,所以由扇形的弧长公式可得:= ×r,解得r=2.
解析
解析:150°=150×=,半径 R=10 cm,
所以 l=αR=×10= (cm).
5. 在直径为20 cm的圆中,150°的圆心角所对的弧长为________.
解析
练 习
1. (口答) 把下列各角从度化为弧度:
(1) 180°; (2) 90°; (3) 45°;
(1) 180°=π;
(2) 90° =90 × =;
(3) 45° =45 × =;
(4) 30°; (5) 120°; (6) 270°.
(4) 30°=30× =;
(5) 120°=120 ×=;
(6) 270° =270 × =;
2. (口答) 把下列各角从弧度化为度:
(1) 2π; (2) ; (3) ; (4) π.
(1) 2π= 2π × =360°;
(2) = ×=90°;
(3) = ×=30°;
(4) =×=120°;
3. 把下列各角从度化为弧度:
(1) 75°;(2) -210°; (3) 135°; (4) 22°30′.
(1) 75°=75× =;
(2) -210°=-210×=-;
(3) 135°=135× =;
(4) 22°30′=22.5°=22.5× =;
4. 把下列各角从弧度化为度:
(1) ; (2) π; (3) -π; (4) -12π.
(1) =× =15°;
(2) = ×=72°;
(3) -=-×=-240°;
(4) -12π=-12π×= - 2160°.
5. 写出与下面的角终边相同的角的集合:
(1) ; (2) .
解 (1) 与终边相同的角的集合为:
{α∣α =2kπ+,k∈Z};
(2) 与终边相同的角的集合为:
{α∣α =2kπ+,k∈Z}.
6. 分别用弧度制表示下列角的集合:
(1) 终边落在 x 轴上的角;
(2) 终边落在 y 轴上的角.
解 (1) 终边落在x轴上的角: {α∣α=kπ,k ∈Z}.
(2) 终边落在y轴上的角: {α∣α=kπ+ ,k ∈Z}.
7. 若 α=-6,则角 α 的终边在 ( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限
A
8. 已知半径为 240 mm的圆上,有一段弧的长是 500 mm,
求此弧所对的圆心角的弧度数.
解 首先设该弧所对的圆心角的度数为α ,代入弧长计算公式可得 240α = 500,然后可求得 α = rad.
习题 7.1
感受·理解
1. 在0°到 360°范内,找出与下列各角终相同的角,
并指出它们是第几象限角:
(1) -265°; (2) 3 900°;
(3) -840°10′; (4) 560°24′.
(1) -265°;
(2) 3 900°;
解 ∵-265°=-360°+95°,95°是第二象限的角,
∴-265°是第二象限的角;
解 ∵3900°=3600°+300°,300°是第四象限的角,
∴3900°是第四象限的角;
(3) -840°10′;
(4) 560°24′.
解 ∵-840°10′=-1080°+239°50′,
239°50′是第三象限的角,
∴ -840°10′是第三象限的角;
解 ∵560°24′=360°+200°24′,
200°24′是第三象限的角,
∴ 560°24′是第三象限的角;
2. 分别写出与下列各角终边相同的角的集合,并把集合
中适合 -360°≤α≤360°的元素α写出来:
(1) 60°;
(2) -75°;
解 由题意可知: A={x∣x = k·360°+60°,k∈Z},
当k=0, -1时, α=60°, -300°.
解 由题意可知: B={x∣x = k·360°-75°,k∈Z},
当k=0, 1时, α=-75°, 285°.
(3) 90°;
(4) -180°.
解 由题意可知: C={x∣x = k·360°+90°,k∈Z},
当k=0, -1时, α=90°, -270°.
解 由题意可知: D={x∣x =k·360°-180°,k∈Z},
当k=0, 1时, α=-180°, 180°.
3. 分别把下列各角从度化为弧度:
(1) 12°30′;
(2) -200°;
解 12°30′ = 12.5°=·π =;
解 -200°=·π = - ;
(3) 355°;
(4) -186°45′.
解 355°=·π =;
解 -186°45′=-186.75°=·π =-;
4. 分别把下列各角从弧度化为度:
(1)-; (2) ; (3) ; (4) 1.4.
解 (1) - ·=-75°;
(2) =480°;
(3) = · = ;
(4) 1.4=1.4· = .
5. 终边落在直线 y=x 上的角的集合如何表示
解 终边落在直线 y=x 上的角的集合为与 , 同终边的角组成的集合,
与同终边的角可表示为: +2kπ,k∈Z,
与同终边的角可表示为: +2kπ= +π+2kπ = +(2k+1)π ,k∈Z,
所以终边落在直线y=x上的角的集合为{α|α=+kπ,k∈Z}.
6. 把下列各角化成 α+2kπ (0≤α<2,k∈Z)的形式,并
分别指出它们是第几象限角:
(1) ; (2) -1500°;
(1) =2π+,是第四象限角.
(2) -1500°= -1800°+300°= -10π+,是第四象限角.
(3) -=-4π+,是第三象限角;
(4) 672°=360°+312°=2π+,是第四象限角;
(3) -; (4) 672°.
7. 如果 α 与120°角终边相同,那么是第几象限角
解 ∵ α与120°终边相同,
∴ α=120°+k·360°(k∈Z),
∴ =60°+k·180°(k∈Z),
当k=2n(n∈Z)时, 为第一象限角,
当 k=2n+1 (n∈Z) 时,
=60°+(2n+1)·180°= 240°+n·360°,
为第三象限角.
∴ 为第一或第三象限角.
8. 已知扇形的半径为 10 cm,圆心角为 60°,求扇形的
弧长和面积.
解 ∵扇形的半径 r=10,圆心角α=60°=,
∴弧长:l=rα=10×= (cm).
面积:S=lr =××10= (cm2).
9. 蒸汽机飞轮的直径为 1.2 m,以300 r/min(转/分)的速度
作逆时针旋转,求:
(1)飞轮1s 内转过的弧度数;
解 ∵ 飞轮转速 300 r/min (转/分) = 5r/s (转/秒),
而且飞轮作逆时针旋转,
∴ 它每 1s 转过的弧度数为 5×2π=10π.
(2) 轮周上一点 1s 内所经过的路程.
解 轮上一点每 1s 所转过的弧长为:
L= αr = 10π×0.6 =6π米
思考·运用
10. 已知 α=,角 β 的终边与角 α 的终边关于直线 y=x
对称,求 β 的集合.
解 当 β∈[0,2π) 时,
∵∠α=,且角β的终边与∠α 的终边关于直线 y=x 对称,可得β=,
故当β∈R时,角β的取值集合是{β|β =+2kπ, k∈Z}.
11. 如图,写出终边落在阴影部分的角的集合(包括边界).
根据边界来确定角的集合,得:{θ∣kπ+≤θ≤kπ+ k∈Z}
根据边界来确定角的集合,得:{θ∣2kπ-≤θ≤2kπ+ k∈Z}
探究·拓展
12. 设 θ 是第一象限角,试探究:
(1) 2θ 一定不是第几象限角
解 ∵ θ是第一象限角,
∴ 2kπ <θ<2kπ+,k∈Z;
∴ 4kπ<2θ<4kπ+π, k∈Z;
∴ 2θ不是第三、四象限角;
(2) 是第几象限角
解 ∵2kπ<θ<2kπ+,k∈Z;
∴ <<+,k∈Z;
∴ k=0时,0<<,是第一象限角;
k=1时, <<,是第二象限角;
k=2时, <<,是第二象限角;
k=3时, <<,是第一象限角;
综上, 是第一、二、三象限角.
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
