8.1 二分法与求方程近似解 课件(共110张PPT) 2023-2024学年高一数学苏教版(2019)必修第一册
文档属性
| 名称 | 8.1 二分法与求方程近似解 课件(共110张PPT) 2023-2024学年高一数学苏教版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 69.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 23:40:16 | ||
图片预览











文档简介
(共110张PPT)
第8章
函数应用
8 . 1
二分法与求方程近似解
函数是研究事物变化过程的数学模型,而方程刻画的则是相等关系成立的某种状态.我们可以从事物变化过程中考察某个状态,也可以通过对若干状态的考察来认识变化的过程,这样就产生了函数与方程的思想. 本节将着重研究函数与方程的关系.
● 函数与方程有什么关系
● 如何运用函数的知识研究方程的解
8.1.1
函数的零点
前面我们学习过,使二次函数 y=ax2+bx+c (a,b,c ∈R,a≠0) 的值为0的实数 x 称为二次函数 y=ax2+bx+c 的零点.
因此,二次函数 y=ax2+bx+c 的零点就是关于 x 的一元二次方程 ax2+bx+c=0 的实数解,也是二次函数y=ax2+bx+c 的图象与 x 轴交点的横坐标.
一、函数的零点
(1) 概念:
一般地,我们把使函数 y=f(x) 的值为0的_______称为函数 y=f(x) 的零点.
实数 x
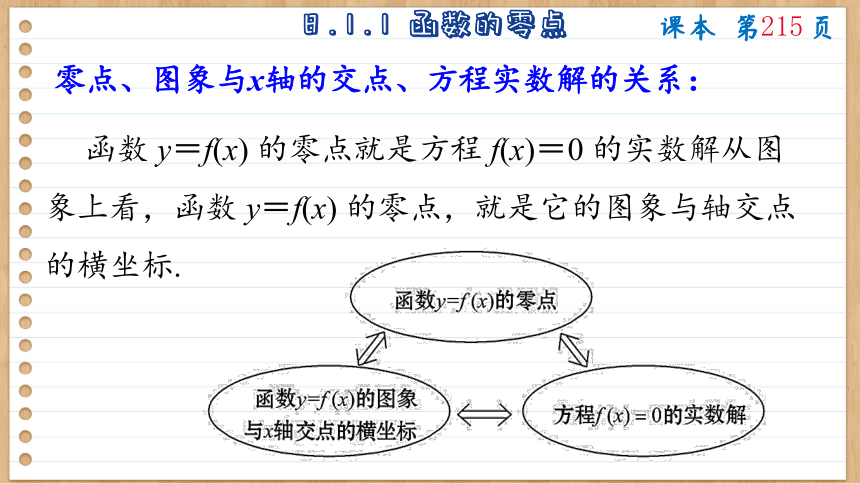
零点、图象与x轴的交点、方程实数解的关系:
函数 y=f(x) 的零点就是方程 f(x)=0 的实数解从图象上看,函数 y=f(x) 的零点,就是它的图象与轴交点的横坐标.
(2) 本质:
方程 f(x)=0 的根、函数 y=f(x) 的图象与 x 轴的公共点的横坐标.
(3) 应用:
利用零点、图象与 x 轴的交点、方程实数解的关系,实现三种问题的相互转化.
【思考】
函数的零点是点吗
提示:不是,是使 f(x)=0 的实数x,是方程 f(x)=0 的根.
对于函数 f(x)=x2-2x-1在区间(2,3)上是否存在零点这个问题,可以通过解方程或观察函数图象的方法来解决,我们还可以进行下面的思考:
如图,因为 f(2)=-1<0,f(3)=2>0,而二次函数 f(x)=x2-2x-1 在区间[2,3] 上的图象是不间断的,这表明此函数图象在区间(2,3)上一定穿过 x 轴,即函数在区间(2,3)上存在零点.
二、函数零点范围的判定
(1)条件:函数 y=f(x) 在区间 [a,b] 上的图象是一条不
间断的曲线,且有_____________;
(2) 结论:函数 y=f(x) 在区间 (a,b) 上有零点.
(3) 本质:利用函数的性质判断零点的存在性.
(4) 应用:判断零点的存在性、求参数的范围等.
f(a)f(b)<0
【思考】
函数 y=f(x) 在区间 (a,b) 上有零点,是不是一定有f(a)f(b)<0?
提示:不一定,如f(x)=x2 在区间(-1,1) 上有零点0,
但是 f(-1)f(1) =1×1=1>0.
例 1
证明:函数 f(x)=x3+x2+1 在区间(-2,-1)上存在零点.
解:因为
f(-2)=(-2)3+(-2)2+1=-3<0,
f(-1)=(-1)3+(-1)2+1=1>0.
且函数 f(x)在区间[-2,-1]上的图象是不间断的,所以函数 f(x)在区间(-2,-1)上存在零点.
例 2
求证:函数 f(x)=2x+2x-3 有零点.
解: 因为
f(0)=20+2×0-3=-2<0,
f(1)=21+2×1-3=1>0,
且函数 f(x) 在区间[0,1] 上的图象是不间断的,所以函数 f(x)=2x+2x-3在区间(0,1)上有零点,从而函数 f(x) =2x+2x-3 有零点.
思 考
如果 x0 是二次函数 y=f(x) 的零点,且 m<x0<n,那么f(m)f(n)<0一定成立吗
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1)函数 y=f(x) 在区间 [a,b] 上的图象是一条连续不断的曲线,且有 f(a)f(b)<0,则函数在区间(a,b)内有唯一的零点. ( )
(2) 若函数y=f(x)在区间(a,b)上f(a)·f(b)>0,则在区间(a,b)内一定没有零点. ( )
(3) 函数 f(x) =x2-x+1有零点. ( )
2. 已知定义在R上的函数f(x)的图象是连续的,且其中的四组对应值如表,那么在下列区间中,函数f(x)不一定存在零点的是 ( )
A.(1,2) B.[1,3] C.[2,5) D.(3,5)
x 1 2 3 5
f(x) 3 -1 2 0
D
解析
解析:由题表可知,f(1)=3,f(2)=-1,f(3)=2,f(5)=0.
由f(1) f(2)<0,可知函数f(x)在(1,2)上一定有零点;
则函数 f(x) 在 [1,3] 上一定有零点;
由f(2) f(3) <0,可知函数f(x)在(2,3)上一定有零点,则函数f(x)在[2,5)上一定有零点;
由f(3)>0,f(5)=0,可知f(x)在(3,5)上不一定有零点.
所以函数f(x)不一定存在零点的区间是(3,5).
3. 函数 f(x)=lnx-6 的零点是________.
e6
解析:令 f(x) =ln x-6=0,则 ln x=6,解得 x=e6.
解析
【跟踪训练】
1. 函数 f(x)=log2(2x+1) 的零点是 ( )
A.1 B.0 C.(0,0) D.(1,1)
B
解析:令 log2(2x+1)= 0,解得 x=0.
解析
2. 已知 m 是函数 f(x)=-2x+2 的零点,则实数 m∈
( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
B
解析:由 f(x)=-2x+2=0可得,+2=2x.
作出函数 y=+2 与 y=2x 的图象如图所示.
当0<x<1时,f(x)>0 恒成立,没有零点,
因为f(1) =1>0,f(2)=-2<0,故在 (1,2)
上有零点,结合图象可知,当x>2时,+2<2x,
即 y=+2恒在y=2x的下方.故 m∈(1,2).
解析
解析:函数 f(x)=ex+3x+1 是连续函数,
因为f(-1) = e-1-3+1<0, f(-) = e - +1>0
故函数的零点所在的区间为(-1,-)
-
3. 函数 f(x)=ex+3x+1 的零点所在的区间为( )
A. (-2,-1) B. (-1,-)
C. (-,0) D. (0,)
B
解析
4. 函数 y=x2-bx+1有一个零点,则b=________.
±2
解析:因为函数有一个零点,所以 Δ=b2-4=0,
所以 b=±2.
解析
解析:显然 x=0 不是函数F(x)的零点,令F(x)=xf(x)-1=0,则f(x)=.故函数 F(x) 的零点个数即为函数
f(x)的图象与函数g(x)=的图象的交点个
数,在同一坐标系中作两函数图象如图:
由图可知,函数f(x)与函数g(x)的图象有5
个交点,即函数F(x)有5个零点.
5. 已知函数 f(x)=|x2-5|-2,则函数F(x)=xf(x) -1的零
点的个数为________.
解析
5
练 习
1. 画出函数y=x2+x-2的图象,并指出函数y=x2+x-2
的零点.
由题可知该函数为二次函数,表示的图象是抛物线,其中a=1>0,抛物线开口向上,对称轴 x=-=-,顶点坐标(-,-),与x轴交点(-2,0),(1,0),
画出函数大致草图如下:
由图象可知:
函数 y=x2+x-2 的零点为 x=1或 x=-2.
2. 求下列函数的零点:
(1) y=2x+3;
解 由 y=0 得 2x+3=0,解得 x=-,
所以函数的零点是-.
(2) y=x2+4x;
解 由 y=0 得 x2+4x=0,解得 x=0或 x=-4,
所以函数的零点是0或-4.
解 由 y=0 得 3x-9=0,解得 x=2,
所以函数的零点是 2.
(3) y=3x-9;
(4) y=log x.
解 由 y=0 得 log x =0,解得 x=1,
所以函数的零点是 1 .
3. 已知数 f(x)=3x-x2,那么方程 f(x)=0 在区间[-1,0]
上有实数解吗 为什么
4. 证明:(1)函数 f(x) =x2+6x+4 有两个不同的零点;
证明:
方程 x2+6x+4=0的判别式 =62-4×4 =20>0,
∴方程 f(x)=0 有两个不同的实数解,
∴ 函数 f(x)=x2+6x+4 有两个不同的零点.
(2) 函数 f(x)=x3+3x-1 在区间(0,1)上有零点.
证明:∵ f(0)=03+3×0-1=-1<0,
f(1)=13+3×1-1=3>0,
且函数f(x)在区间[0,1] 上的图象是不间断的,
∴ f(x) 在区间 (0,1) 上有零点.
5. 函数 f(x)=4x3+x-15 在区间 [1,2] 上是否存在零点
为什么
解 函数 f(x)=4x3+x-15在区间[1,2]上存在零点,
∵ f(1)=-10<0,f(2)=19>0.
∴ f(1)f(2)<0
又∵函数 f(x)=4x3+x-15的图象在区间[1,2]上是一条连续不断的曲线
∴函数 f(x)=4x3+x-15在区间[1,2] 上存在零点.
6. 求证:函数 f(x)=2x+x 在 R 上有零点.
8.1.2
用二分法求方程的近似解
对于方程 lg x=3-x,要求出这个方程的解是较为困难的.我们能否求出这个方程的近似解呢
让我们先从熟悉的一元二次方程开始研究.
例如,求方程 x2-2x-1=0 的实数解就是求函数 f(x) =x2-2x-1 的零点. 根据图8-1-2,我们发现 f(2)<0,f(3)>0.
这表明此函数图象在区间 (2,3) 上有零点,即方程 f(x)=0 在区间(2,3)上有实数解. 又因为在区间(2,3)上函数 f(x) 单调递增,所以方程 x2-2x-1=0 在区间(2,3)上有唯一实数解 x1.
计算得f() =>0,发现 x1∈(2,2.5) ,这样可以进一步缩小 x1 所在的区间.
思 考
你能把此方程的一个根 x1 限制在更小的区间内吗
下面我们利用计算工具来求方程 x2-2x-1=0 的一个近似解(精确到 0.1). 设 f(x)=x2-2x-1,先画出函数的图象.
▲ 图中负号“-”表示此点所对应的函数值为负,正号“+”表示此点所对应的函数值为正,下同.
因为
f(2) =-1<0,f(3)=2>0,
所以在区间(2,3)上,方程x2-2x-1=0有一解,记为x1.
取2与3的平均数2.5.
因为f(2.5)=0.25>0,所以2<x<2.5.
再取2与2.5的平均数2.25.
因为 f(2.25) =-0.43750,所以2.25< x1<2.5.
如此继续下去,得
f(2)<0,f(3)>0 x1∈(2,3),
f(2)<0,f(2.5)>0 x1∈(2,2.5),
f(2.25)<0,f(2.5)>0 x1∈(2.25,2.5),
f(2.375)<0,f(2.5)>0 x1∈(2.375,2.5),
f(2.375)<0,f(2.437 5)>0 x1∈(2.375,2.437 5).
因为 2.375 与 2.437 5 精确到 0.1的近似值都为 2.4,所以此方程的近似解为
x1≈2.4.
利用同样的方法,还可以求出方程的另一个近似解.
二分法
像上面这种求方程近似解的方法称为二分法,它是求一元方程近似解的常用方法.
运用二分法的前提是要先判断某解所在的区间.
例 3
利用计算器,求方程 lg x=3-x 的近似解
(精确到 0.1).
分析 求方程 lg x=3-x 的解可以转化为求函数 f(x)=lg x+x-3 的零点,故可以利用二分法求出题中方程的近似解.
解 分别画出函数 y=lg x 和 y=3-x 的图象,如图所示.
在两个函数图象的交点处,函数值相等. 因此,这个点的横坐标就是方程 lgx=3-x 的解由函数 y=lgx 与 y=3-x 的图象可以发现,方程 lg x=3-x 有唯一解,记为x1,并这个解在区间 (2,3) 内.
设 f(x)=lgx+x-3,用计算器计算,得
f(2)<0,f(3)>0 x1∈(2,3),
f(2.5)<0,f(3)>0 x1∈(2.5,3),
f(2.5)<0,f(2.75)>0 x1∈(2.5,2.75),
f(2.5)<0,f(2.625)>0 x1∈(2.5,2.625),
f(2.562 5)<0,f(2.625)>0 x1∈(2.562 5,2.625).
因为 2.5625与2.625 精确到0.1的近似值都为 2.6,以原方程的近似解为
x1≈2.6.
例 4
利用计算器,求方程 sin x=1-x 的近似解 (精确到 0.1)
解:因为方程 sin x=1-x 可化为 x+sinx-1=0,所以原方程的解即函数 f(x)=x+sinx-1的零点.
先画出函数 y=sinx与函数 y=1-x 的图象,如图 8-1-4 所示.
观察图象,因为
f(0)=-1<0,f(1)=sin1>0,
所以函数 f(x)的零点在区间 (0,1) 内,记为 x0.
取0和1的平均数 0.5,因为
f(0.5)=sin0.5-0.5=-0.020 57<0,
所以动 x0∈ (0.5,1).
取 0.5和1的平均数 0.75,因为
f(0.75)-sin0.75-0.25=0.43164>0,
所以 x0∈(0.5,0.75).
取0.5和0.75的平均数 0.625,因为
f(0.625)=sin0.625-0.375=0.210 10>0,
所以 x0∈(0.5,0.625).
取0.5和0.625的平均数 0.562 5,因为
f(0.562 5)=sin0.562 5-0.437 5=0.095 80>0,
所以 x0∈ (0.5,0.562 5).
取0.5和0.5625的平均数0.53125,因为
f(0.531 25) =sin0.531 25-0.68 75=0.037 86>0,
所以 x0∈(0.5,0.531 25).
因为0.5和0.531 25 精确到 0.1的近似数都是0.5,所以区间(0.5,0.531 25)内的所有数精确到 0.1的近似数都是 0.5,从而 x0≈0.5. 因此,方程 sinx=1-x 的近似解(精确到 0.1)为0.5.
用二分法求方程的一个近似解的操作流程是:
在以上操作过程中,如果存在 c,使得 f(x)=0,那么 c 就是方程 f(x)=0 的一个精确解.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 任何函数的零点都可以用二分法求得. ( )
(2)用二分法求出的函数零点就是精确值. ( )
2. 下列图象与 x 轴均有交点,其中不能用二分法求函数零点的是 ( )
A
解析:只有A中图象与x轴交点两侧的函数值不变号,都是正值,因此不能用二分法.
解析
3. 若函数 f(x)=x3+x2-2x-2的一个零点(正数)附近的函数值用二分法逐次计算,参考数据如表:
x 1 1.5 1.25 1.375 1.4375
f(x) -2 0.625 -0.984 -0.260 0.162
则方程 x3+x2-2x-2=0的一个近似解(精确到0.1)为________.
x≈1.4
解析
解析 因为f(1)f(1.5)<0,所以x0∈(1,1.5);
因为 f(1.437 5)≈0.162>0,
又 f(1.375)≈-0.260<0,
所以 x0∈(1.375,1.437 5),
因为1.375与1.437 5精确到0.1的近似值都是1.4,
所以原方程的近似解为x≈1.4.
【跟踪训练】
1. 用二分法求函数 y=f(x) 在区间 [2,4] 上的唯一零点的近似值时,验证 f(2)·f(4)<0,取区间 (2,4) 的中点 x1==3,计算得 f(2)·f(x1)<0,则此时零点x0所在的区间是( )
A.(2,4) B.(2,3) C.(3,4) D.无法确定
B
解析
解析:由题意可知:对于函数 y=f(x) 在区间 [2,4] 上,有f(2)·f(4)<0,
所以函数在 (2,4) 上有零点.
取区间的中点 x1==3,
因为计算得 f(2)·f(x1)<0,
所以利用函数的零点存在定理得,函数在(2,3)上有零点.
2. 用二分法求函数 f(x)=3x-x-4 的一个零点,其参考数据如下:
f(1.6000)≈0.200 f(1.5875)≈0.133 f(1.5750)≈0.067
f(1.5625)≈0.003 f(1.5562)≈-0.029 f(1.5500)≈-0.060
据此数据,可得方程 3x-x-4=0 的一个近似解 (精确到0.01)为________.
x≈1.56
解析
解析 f(1.562 5)≈0.003>0,f(1.556 2)≈-0.029<0,
方程3x-x-4=0 的一个近似解在(1.556 2,1.562 5)上,
所以精确到0.01的近似解为 x≈1.56.
3. 用二分法求方程 x3-2x-5=0 在区间[2,3]内的实根,
取区间中点x0=2.5,那么下一个有根区间为_______.
(2,2.5)
解析:因为 f(2)<0,f(2.5)>0,f(3)>0,
所以 f(2)f(2.5)<0,f(2.5)f(3) >0.
所以下一个有根区间应为 (2,2.5).
解析
练 习
1. 利用计算器,求方程 x3+3x -1=0 在区间(0,1)上的
近似解 (精确到0.1).
解 设 f(x)=x3+3x-1,
因为 f(0)=0+3×0-1 =-1<0,
f(1)=13+3×1-1=3>0,
取区间 (0,1) 的中点 x1==0.5,
因为 f(0.5)=0.53+3×0.5-1>0.625>0,
所以 f(0)·f(0.5)<0,
因为 ∣0-0.5∣=0.5>0.1,
所以取区间 (0,0.5) 的中点x2= =0.25,
因为 f(0.25)=0.253+3×0.25-1≈-0.23<0,
所以 f(0.25)·f(0.5)<0,
因为 ∣0.25-0.5∣=0.5>0.1,
所以取区间 (0.25,0.5) 的中点 x3= =0.375,
因为 f(0.375)=0.3753+3×0.375-1≈0.18 >0,
所以 f(0.25)·f(0.375)<0,
因为 ∣0.25-0.375∣=0.125>0.1,
所以取区间(0.25,0.375)的中点 x4==0.31.
因为 f(0.31)=0.313+3×0.0.31-1>-0.04<0,
所以 f(0.31)·f(0.375)<0,
因为 ∣0.31-0.375∣=0.065<0.1,
又因为函数 f(x) 在区间 (0.31,0.375) 上连续,
所以方程x3+3x-1=0在区间 (0,1) 上的近似解为0.3.
2. 利用计算器,求方程lgx=1-2x的近似解 (精确到0.1).
解 令f(x)=lgx+2x-1,则 f()=lg<0, f(1)=1>0.
所以函数 f(x)=lgx+2-1在区间(,1)上存在零点,
因为 f()=lg+≈0.375,
所以函数 f(x)=lgx+2x-1在区间(, )上存在零点,
因为 f()=lg+≈0.0459,
所以函数 f(x)=lgx+2x-1在区间(, )上存在零点,
因为 f()=lg+≈-0.1249,
所以函数 f(x)=lgx+2x-1在区间(, )上存在零点,
因为 -= =0.0625<0.1,
所以可取(, )中的数作为方程的近似解,
例如0.6,因此0.6是方程 lgx=1-2x的近似解.
3. 用自己的语言叙述用二分法求方程近似解的基本步骤.
① 给定区间[a,b],验证f(a)·f(b)<0,给定精确度,
② 求区间[a,b]的中点c,
③ 若 f(c)=0,则c就是函数的零点,
若f(a)·f(c)<0,则令b=c (此时零点 x0∈(a,c)),
若f(b)·f(c)<0,则令a=c (此时零点 x0∈(c,b)),
④ 判断是否达到精确度,即若∣b-a∣<,
则得到零点近似值a或b,否则重复② - ④.
4. 用两种方法解方程 2x2=3x-1.
5. 利用计算器,求方程 x3=2x+1 的近似解(精确到0.1).
因为-0.625≈-0.6,-0.5625≈-0.6,
所以取x2=-0.6
因为1.5625 ≈ 1.6,
所以取x3 ≈ 1.6.
综上,方程x3=2x+1的近似解是 x1=1.0,x2≈-0.6,x3≈1.6.
6. 利用计算器,求方程 x-cosx=0 的近似解(精确到0.1).
解:设 f(x)=x-cosx,方程的解为x0,用计算器计算得
f(0)<0,f(1)>0 x0 ∈(0,1),
f(0.5)<0,f(1)>0 x0 ∈(0.5,1),
f(0.5)<0,f(0.75)>0 x0∈( 0.5,0.75 ),
f(0.625)<0,f(0.75)>0 x0∈(0.625,0.75),
f(0.6875)<0,f(0.75)>0 x0∈(0.6875,0.75),
f(0.71875)<0,f(0.75)>0 x0∈(0.71875 ,0.75),
f(0.734 375)<0,f(0.75)>0 x0∈(0.734 375,0.75 ),
f(0.734 375)<0,f(0.742 187 5)>0
x0∈(0.734 375,0.742 187 5)
∵ 0.734375和0.742 1875 精确到0.1 的近似值都是 0.7,
∴x≈0.7.
习题 8.1
感受·理解
1. 说明下列函数在给定的区间上存在零点:
(1) f(x)= lgx+2x-5,(1,3);
(2) f(x)= 2x+x2-7,(1,2);
(3) f(x)= x3+x-1,(0,1);
(4) f(x)= 2x+sinx-l,(0,π).
(1) f(x)= lgx+2x-5,(1,3);
(2) f(x)= 2x+x2-7,(1,2);
(3) f(x)= x3+x-1,(0,1);
(4) f(x)= 2x+sinx-l,(0,π).
2. 求证:方程 x2+x+1=0 没有实数根.
3. 设m为实数若函数 y=mx2-6x+2 的图象与x轴只有1个
公共点,求m的值.
4. 设 k 为实数,若方程 4(x2-3x) +k-3=0没有实数根,
求的取值范围.
5. 求证:方程 5x2+7x-1=0 的根一个在区间(-2,-1)
内,另一个在区间(0,1)内.
证明:设 f(x)=5x2+7x-1,则二次函数f(x)是定义域R上的连续函数,
计算 f(-2)· f(-1)=(20-14-1) ×(5-7-1)<0,
所以 f(x) 的一个零点在区间(-2,1)内,
计算 f(0)·f(1)=(0+0-1) ×(5+7-1) <0,
所以f(x)的一个零点在区间 (0,1)内;
所以方程 5x2+7x-1=0的根一个在区间(-2,-1)内,另一个在区间(0,1)内.
6. 利用计算器,求方程 x2-2x-2=0 的近似解
(精确到0.1).
解 由条件x2-2x-2=0 两个根设为 x1,x2,
则x1+x2=2,
设函数为f(x)=x2-2x-2,设函数的零点为x0,
因为 f(0)=-2<0,f(-1)=1>0,
则 x0∈(-1,0) ,
取(-1,0)的中间值-0.5,所以f(-0.5) =-0.75<0,
则f(-0.5)f(-1)<0,则 x0∈(-1,-0.5),
取 (-1,-0.5)中间值-0.75,
计算得 f(-0.75)=0.0625>0,
所以 f(-0.75)f(-0.5)<0,则 x0∈(-0.75, -0.5),
取(-0.75, -0.5)中间值-0.625,
计算得 f(-0.625)=-0.3594<0,
所以 f(-0.75)f(-0.625)<0,则x0∈(-0.75,-0.625),
取(-0.75,-0.625)中间值-0.6875,
计算得 f(-0.6875) =-0.1523<0,
所以 f(-0.75)f(-0.6875)<0,则x0∈(-0.75,-0.6875),
因为∣-0.75-(-0.6875)∣=0.0625<0.1,
则方程 x2-2x-2=0的近似解为x1≈-0.7,
同理可得方程另一个近似解为x2≈2.7,
则方程两个近似解为-0.7和2.7.
7. 用多种方法解方程 x2=3x+10.
解法1:方程 x2=3x+10可化为 x2-3x-10=0,
即 (x+2)(x-5) =0,
∴x1=-2,x2=5.
解法2:方程 x2=3x+10 可化为 x2-3x-10=0,
∴ =b2-4ac= (-3)2-4×1× (-10)
=9+40=49,
∵ x=,
x1= = = = -2,
x2= = = = 5,
∴ x1=-2,x2=5.
思考·运用
8. 设 m 为实数,若方程 7x2-(m+13)x-m-2=0 的一
个根在区间 (0,1) 内,另一个根在区间 (1,2) 内,
求 m 的取值范围.
解 设 f(x)=7x2-(m+13)x-m-2,
∵方程 7x2-(m+13)x- m-2=0的一个根在区间(0,1)内,另一个根在区间(1,2)内,
解得-4<m<-2,
∴ m的取值范围是(-4,-2).
9. 设 k 为实数,若函数 f(x)=x2-2x+k 在区间[-1,0]
上有零点,求 k 的取值范围.
解 f(x)=0等价于k=2x-x2 ,
构造函数 g(x)=2x-x2 ,x∈[-1,0],
故只需要k的范围是函数g(x)的值域,
即原函数 f(x) 在区间 [-1,0] 上有零点,
g′(x) = 2xln2-2x,g′′(x) = 2x(ln2)2-2,
显然 g′′(x) 在区间[-1,0]上单调递增,
故 g′′(x) ≤ g′′(0)=(ln2)2 - 2<0,
所以 g′(x) 在区间[-1,0]上单调递减,
g′(x)≥g′(0) = ln2>0,
所以 g(x) 在区间[-1,0] 上单调递增,g(0)=1,
g(-1)=-1=-,故g(x)∈[-,1],
即k的取值范围为[-,1].
10. 设 a 为实数,函数 f(x)=x2-ax-1,且函数 f(x) 在区
间 [-1,2] 上有唯的零点,求 a 的取值范围.
解 ∵ =(-a)2-4×(-1) =a2+4>0,
∴ 方程f(a)=0有两个不等实根.
①当 f(-1)=0时,1+a-1=a=0.
此时f(a)=x2-1.
令 f(x)=0,解得 x=-1或 x=1,
此时 f(x) 在区间[-1,2] 上有两个零点,不合题意,舍掉.
② 当f(2)=0时,4-2a-1=3-2a=0,
解得 a=,
此时 f(x)=x2-x-1.
令 f(x)=0,解得 x=-或x=2,
此时 f(x) 在区间[-1,2] 上有两个零点,不合题意,舍去.
③ 若函数 f(x) 在区间(-1,2)上有唯一的零点,
则只需 f(-1)·f(2)<0,
即a(3-2a)<0,即a(2a-3)>0,
解得 a<0 或 a>,
故a的取值范围是{x∣a<0或a>}.
11. 利用计算器,求下列方程的近似解 (精确到 0.1):
(1) lg(2x) =-x+1;
(2) 3x =x+4;
(3) 2x-cosx -1=0.
(1) lg(2x) =-x+1;
解 设函数 f(x)=lg(2x)+x-1,
则 f(0.7)=lg1.4+0.7-1≈-0.15<0,
f(0.75)=lg1.5+0.75-1≈-0.07<0,
f(0.8)=lg1.6+0.8-1≈0.004>0,
所以f(x)=lg(2x)+x-1=0,
即方程 lg(2x)=-x+1的解约为0.8.
(2) 3x =x+4;
解 设函数 f(x)=3x-x-4,
则f(-4.0)=3-4.0 +4.0-4≈0.012>0,
f(-3.95)=3-3.95+3.95-4≈-0.037<0,
f(1.55)=31.55-1.55-4≈-0.060<0,
f(1.60)=31.60 -1.60-4≈0.20>0,
所以 f(x)=3x-x-4=0,即方程 3x=x+4的两个解约为-4.0和1.6.
(3) 2x-cosx -1=0.
解 设函数 f(x) =2x-cos x -1,
则f(0.8) =1.6-cos0.8-1≈-0.10<0,
f(0.85) =1.7-cos0.85-1≈0.04>0,
所以方程 2x-cosx-1=0 的解约为0.8.
探究·拓展
12. 已知定义在 R 上的函数 y=f(x)的图象是一条不间断的
曲线,f(a)≠f(b),其中a<b,设 F(x)=f(x)-,
求证:函数 F(x) 在区间 (a,b) 上有零点.
证明:∵ f(x) 在(a,b)上不间断,
∴ F(x)=f(x) - 在 (a,b)上连续.
本课结束
This lesson is over
THANKS!
第8章
函数应用
8 . 1
二分法与求方程近似解
函数是研究事物变化过程的数学模型,而方程刻画的则是相等关系成立的某种状态.我们可以从事物变化过程中考察某个状态,也可以通过对若干状态的考察来认识变化的过程,这样就产生了函数与方程的思想. 本节将着重研究函数与方程的关系.
● 函数与方程有什么关系
● 如何运用函数的知识研究方程的解
8.1.1
函数的零点
前面我们学习过,使二次函数 y=ax2+bx+c (a,b,c ∈R,a≠0) 的值为0的实数 x 称为二次函数 y=ax2+bx+c 的零点.
因此,二次函数 y=ax2+bx+c 的零点就是关于 x 的一元二次方程 ax2+bx+c=0 的实数解,也是二次函数y=ax2+bx+c 的图象与 x 轴交点的横坐标.
一、函数的零点
(1) 概念:
一般地,我们把使函数 y=f(x) 的值为0的_______称为函数 y=f(x) 的零点.
实数 x
零点、图象与x轴的交点、方程实数解的关系:
函数 y=f(x) 的零点就是方程 f(x)=0 的实数解从图象上看,函数 y=f(x) 的零点,就是它的图象与轴交点的横坐标.
(2) 本质:
方程 f(x)=0 的根、函数 y=f(x) 的图象与 x 轴的公共点的横坐标.
(3) 应用:
利用零点、图象与 x 轴的交点、方程实数解的关系,实现三种问题的相互转化.
【思考】
函数的零点是点吗
提示:不是,是使 f(x)=0 的实数x,是方程 f(x)=0 的根.
对于函数 f(x)=x2-2x-1在区间(2,3)上是否存在零点这个问题,可以通过解方程或观察函数图象的方法来解决,我们还可以进行下面的思考:
如图,因为 f(2)=-1<0,f(3)=2>0,而二次函数 f(x)=x2-2x-1 在区间[2,3] 上的图象是不间断的,这表明此函数图象在区间(2,3)上一定穿过 x 轴,即函数在区间(2,3)上存在零点.
二、函数零点范围的判定
(1)条件:函数 y=f(x) 在区间 [a,b] 上的图象是一条不
间断的曲线,且有_____________;
(2) 结论:函数 y=f(x) 在区间 (a,b) 上有零点.
(3) 本质:利用函数的性质判断零点的存在性.
(4) 应用:判断零点的存在性、求参数的范围等.
f(a)f(b)<0
【思考】
函数 y=f(x) 在区间 (a,b) 上有零点,是不是一定有f(a)f(b)<0?
提示:不一定,如f(x)=x2 在区间(-1,1) 上有零点0,
但是 f(-1)f(1) =1×1=1>0.
例 1
证明:函数 f(x)=x3+x2+1 在区间(-2,-1)上存在零点.
解:因为
f(-2)=(-2)3+(-2)2+1=-3<0,
f(-1)=(-1)3+(-1)2+1=1>0.
且函数 f(x)在区间[-2,-1]上的图象是不间断的,所以函数 f(x)在区间(-2,-1)上存在零点.
例 2
求证:函数 f(x)=2x+2x-3 有零点.
解: 因为
f(0)=20+2×0-3=-2<0,
f(1)=21+2×1-3=1>0,
且函数 f(x) 在区间[0,1] 上的图象是不间断的,所以函数 f(x)=2x+2x-3在区间(0,1)上有零点,从而函数 f(x) =2x+2x-3 有零点.
思 考
如果 x0 是二次函数 y=f(x) 的零点,且 m<x0<n,那么f(m)f(n)<0一定成立吗
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1)函数 y=f(x) 在区间 [a,b] 上的图象是一条连续不断的曲线,且有 f(a)f(b)<0,则函数在区间(a,b)内有唯一的零点. ( )
(2) 若函数y=f(x)在区间(a,b)上f(a)·f(b)>0,则在区间(a,b)内一定没有零点. ( )
(3) 函数 f(x) =x2-x+1有零点. ( )
2. 已知定义在R上的函数f(x)的图象是连续的,且其中的四组对应值如表,那么在下列区间中,函数f(x)不一定存在零点的是 ( )
A.(1,2) B.[1,3] C.[2,5) D.(3,5)
x 1 2 3 5
f(x) 3 -1 2 0
D
解析
解析:由题表可知,f(1)=3,f(2)=-1,f(3)=2,f(5)=0.
由f(1) f(2)<0,可知函数f(x)在(1,2)上一定有零点;
则函数 f(x) 在 [1,3] 上一定有零点;
由f(2) f(3) <0,可知函数f(x)在(2,3)上一定有零点,则函数f(x)在[2,5)上一定有零点;
由f(3)>0,f(5)=0,可知f(x)在(3,5)上不一定有零点.
所以函数f(x)不一定存在零点的区间是(3,5).
3. 函数 f(x)=lnx-6 的零点是________.
e6
解析:令 f(x) =ln x-6=0,则 ln x=6,解得 x=e6.
解析
【跟踪训练】
1. 函数 f(x)=log2(2x+1) 的零点是 ( )
A.1 B.0 C.(0,0) D.(1,1)
B
解析:令 log2(2x+1)= 0,解得 x=0.
解析
2. 已知 m 是函数 f(x)=-2x+2 的零点,则实数 m∈
( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
B
解析:由 f(x)=-2x+2=0可得,+2=2x.
作出函数 y=+2 与 y=2x 的图象如图所示.
当0<x<1时,f(x)>0 恒成立,没有零点,
因为f(1) =1>0,f(2)=-2<0,故在 (1,2)
上有零点,结合图象可知,当x>2时,+2<2x,
即 y=+2恒在y=2x的下方.故 m∈(1,2).
解析
解析:函数 f(x)=ex+3x+1 是连续函数,
因为f(-1) = e-1-3+1<0, f(-) = e - +1>0
故函数的零点所在的区间为(-1,-)
-
3. 函数 f(x)=ex+3x+1 的零点所在的区间为( )
A. (-2,-1) B. (-1,-)
C. (-,0) D. (0,)
B
解析
4. 函数 y=x2-bx+1有一个零点,则b=________.
±2
解析:因为函数有一个零点,所以 Δ=b2-4=0,
所以 b=±2.
解析
解析:显然 x=0 不是函数F(x)的零点,令F(x)=xf(x)-1=0,则f(x)=.故函数 F(x) 的零点个数即为函数
f(x)的图象与函数g(x)=的图象的交点个
数,在同一坐标系中作两函数图象如图:
由图可知,函数f(x)与函数g(x)的图象有5
个交点,即函数F(x)有5个零点.
5. 已知函数 f(x)=|x2-5|-2,则函数F(x)=xf(x) -1的零
点的个数为________.
解析
5
练 习
1. 画出函数y=x2+x-2的图象,并指出函数y=x2+x-2
的零点.
由题可知该函数为二次函数,表示的图象是抛物线,其中a=1>0,抛物线开口向上,对称轴 x=-=-,顶点坐标(-,-),与x轴交点(-2,0),(1,0),
画出函数大致草图如下:
由图象可知:
函数 y=x2+x-2 的零点为 x=1或 x=-2.
2. 求下列函数的零点:
(1) y=2x+3;
解 由 y=0 得 2x+3=0,解得 x=-,
所以函数的零点是-.
(2) y=x2+4x;
解 由 y=0 得 x2+4x=0,解得 x=0或 x=-4,
所以函数的零点是0或-4.
解 由 y=0 得 3x-9=0,解得 x=2,
所以函数的零点是 2.
(3) y=3x-9;
(4) y=log x.
解 由 y=0 得 log x =0,解得 x=1,
所以函数的零点是 1 .
3. 已知数 f(x)=3x-x2,那么方程 f(x)=0 在区间[-1,0]
上有实数解吗 为什么
4. 证明:(1)函数 f(x) =x2+6x+4 有两个不同的零点;
证明:
方程 x2+6x+4=0的判别式 =62-4×4 =20>0,
∴方程 f(x)=0 有两个不同的实数解,
∴ 函数 f(x)=x2+6x+4 有两个不同的零点.
(2) 函数 f(x)=x3+3x-1 在区间(0,1)上有零点.
证明:∵ f(0)=03+3×0-1=-1<0,
f(1)=13+3×1-1=3>0,
且函数f(x)在区间[0,1] 上的图象是不间断的,
∴ f(x) 在区间 (0,1) 上有零点.
5. 函数 f(x)=4x3+x-15 在区间 [1,2] 上是否存在零点
为什么
解 函数 f(x)=4x3+x-15在区间[1,2]上存在零点,
∵ f(1)=-10<0,f(2)=19>0.
∴ f(1)f(2)<0
又∵函数 f(x)=4x3+x-15的图象在区间[1,2]上是一条连续不断的曲线
∴函数 f(x)=4x3+x-15在区间[1,2] 上存在零点.
6. 求证:函数 f(x)=2x+x 在 R 上有零点.
8.1.2
用二分法求方程的近似解
对于方程 lg x=3-x,要求出这个方程的解是较为困难的.我们能否求出这个方程的近似解呢
让我们先从熟悉的一元二次方程开始研究.
例如,求方程 x2-2x-1=0 的实数解就是求函数 f(x) =x2-2x-1 的零点. 根据图8-1-2,我们发现 f(2)<0,f(3)>0.
这表明此函数图象在区间 (2,3) 上有零点,即方程 f(x)=0 在区间(2,3)上有实数解. 又因为在区间(2,3)上函数 f(x) 单调递增,所以方程 x2-2x-1=0 在区间(2,3)上有唯一实数解 x1.
计算得f() =>0,发现 x1∈(2,2.5) ,这样可以进一步缩小 x1 所在的区间.
思 考
你能把此方程的一个根 x1 限制在更小的区间内吗
下面我们利用计算工具来求方程 x2-2x-1=0 的一个近似解(精确到 0.1). 设 f(x)=x2-2x-1,先画出函数的图象.
▲ 图中负号“-”表示此点所对应的函数值为负,正号“+”表示此点所对应的函数值为正,下同.
因为
f(2) =-1<0,f(3)=2>0,
所以在区间(2,3)上,方程x2-2x-1=0有一解,记为x1.
取2与3的平均数2.5.
因为f(2.5)=0.25>0,所以2<x<2.5.
再取2与2.5的平均数2.25.
因为 f(2.25) =-0.43750,所以2.25< x1<2.5.
如此继续下去,得
f(2)<0,f(3)>0 x1∈(2,3),
f(2)<0,f(2.5)>0 x1∈(2,2.5),
f(2.25)<0,f(2.5)>0 x1∈(2.25,2.5),
f(2.375)<0,f(2.5)>0 x1∈(2.375,2.5),
f(2.375)<0,f(2.437 5)>0 x1∈(2.375,2.437 5).
因为 2.375 与 2.437 5 精确到 0.1的近似值都为 2.4,所以此方程的近似解为
x1≈2.4.
利用同样的方法,还可以求出方程的另一个近似解.
二分法
像上面这种求方程近似解的方法称为二分法,它是求一元方程近似解的常用方法.
运用二分法的前提是要先判断某解所在的区间.
例 3
利用计算器,求方程 lg x=3-x 的近似解
(精确到 0.1).
分析 求方程 lg x=3-x 的解可以转化为求函数 f(x)=lg x+x-3 的零点,故可以利用二分法求出题中方程的近似解.
解 分别画出函数 y=lg x 和 y=3-x 的图象,如图所示.
在两个函数图象的交点处,函数值相等. 因此,这个点的横坐标就是方程 lgx=3-x 的解由函数 y=lgx 与 y=3-x 的图象可以发现,方程 lg x=3-x 有唯一解,记为x1,并这个解在区间 (2,3) 内.
设 f(x)=lgx+x-3,用计算器计算,得
f(2)<0,f(3)>0 x1∈(2,3),
f(2.5)<0,f(3)>0 x1∈(2.5,3),
f(2.5)<0,f(2.75)>0 x1∈(2.5,2.75),
f(2.5)<0,f(2.625)>0 x1∈(2.5,2.625),
f(2.562 5)<0,f(2.625)>0 x1∈(2.562 5,2.625).
因为 2.5625与2.625 精确到0.1的近似值都为 2.6,以原方程的近似解为
x1≈2.6.
例 4
利用计算器,求方程 sin x=1-x 的近似解 (精确到 0.1)
解:因为方程 sin x=1-x 可化为 x+sinx-1=0,所以原方程的解即函数 f(x)=x+sinx-1的零点.
先画出函数 y=sinx与函数 y=1-x 的图象,如图 8-1-4 所示.
观察图象,因为
f(0)=-1<0,f(1)=sin1>0,
所以函数 f(x)的零点在区间 (0,1) 内,记为 x0.
取0和1的平均数 0.5,因为
f(0.5)=sin0.5-0.5=-0.020 57<0,
所以动 x0∈ (0.5,1).
取 0.5和1的平均数 0.75,因为
f(0.75)-sin0.75-0.25=0.43164>0,
所以 x0∈(0.5,0.75).
取0.5和0.75的平均数 0.625,因为
f(0.625)=sin0.625-0.375=0.210 10>0,
所以 x0∈(0.5,0.625).
取0.5和0.625的平均数 0.562 5,因为
f(0.562 5)=sin0.562 5-0.437 5=0.095 80>0,
所以 x0∈ (0.5,0.562 5).
取0.5和0.5625的平均数0.53125,因为
f(0.531 25) =sin0.531 25-0.68 75=0.037 86>0,
所以 x0∈(0.5,0.531 25).
因为0.5和0.531 25 精确到 0.1的近似数都是0.5,所以区间(0.5,0.531 25)内的所有数精确到 0.1的近似数都是 0.5,从而 x0≈0.5. 因此,方程 sinx=1-x 的近似解(精确到 0.1)为0.5.
用二分法求方程的一个近似解的操作流程是:
在以上操作过程中,如果存在 c,使得 f(x)=0,那么 c 就是方程 f(x)=0 的一个精确解.
【基础小测】
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 任何函数的零点都可以用二分法求得. ( )
(2)用二分法求出的函数零点就是精确值. ( )
2. 下列图象与 x 轴均有交点,其中不能用二分法求函数零点的是 ( )
A
解析:只有A中图象与x轴交点两侧的函数值不变号,都是正值,因此不能用二分法.
解析
3. 若函数 f(x)=x3+x2-2x-2的一个零点(正数)附近的函数值用二分法逐次计算,参考数据如表:
x 1 1.5 1.25 1.375 1.4375
f(x) -2 0.625 -0.984 -0.260 0.162
则方程 x3+x2-2x-2=0的一个近似解(精确到0.1)为________.
x≈1.4
解析
解析 因为f(1)f(1.5)<0,所以x0∈(1,1.5);
因为 f(1.437 5)≈0.162>0,
又 f(1.375)≈-0.260<0,
所以 x0∈(1.375,1.437 5),
因为1.375与1.437 5精确到0.1的近似值都是1.4,
所以原方程的近似解为x≈1.4.
【跟踪训练】
1. 用二分法求函数 y=f(x) 在区间 [2,4] 上的唯一零点的近似值时,验证 f(2)·f(4)<0,取区间 (2,4) 的中点 x1==3,计算得 f(2)·f(x1)<0,则此时零点x0所在的区间是( )
A.(2,4) B.(2,3) C.(3,4) D.无法确定
B
解析
解析:由题意可知:对于函数 y=f(x) 在区间 [2,4] 上,有f(2)·f(4)<0,
所以函数在 (2,4) 上有零点.
取区间的中点 x1==3,
因为计算得 f(2)·f(x1)<0,
所以利用函数的零点存在定理得,函数在(2,3)上有零点.
2. 用二分法求函数 f(x)=3x-x-4 的一个零点,其参考数据如下:
f(1.6000)≈0.200 f(1.5875)≈0.133 f(1.5750)≈0.067
f(1.5625)≈0.003 f(1.5562)≈-0.029 f(1.5500)≈-0.060
据此数据,可得方程 3x-x-4=0 的一个近似解 (精确到0.01)为________.
x≈1.56
解析
解析 f(1.562 5)≈0.003>0,f(1.556 2)≈-0.029<0,
方程3x-x-4=0 的一个近似解在(1.556 2,1.562 5)上,
所以精确到0.01的近似解为 x≈1.56.
3. 用二分法求方程 x3-2x-5=0 在区间[2,3]内的实根,
取区间中点x0=2.5,那么下一个有根区间为_______.
(2,2.5)
解析:因为 f(2)<0,f(2.5)>0,f(3)>0,
所以 f(2)f(2.5)<0,f(2.5)f(3) >0.
所以下一个有根区间应为 (2,2.5).
解析
练 习
1. 利用计算器,求方程 x3+3x -1=0 在区间(0,1)上的
近似解 (精确到0.1).
解 设 f(x)=x3+3x-1,
因为 f(0)=0+3×0-1 =-1<0,
f(1)=13+3×1-1=3>0,
取区间 (0,1) 的中点 x1==0.5,
因为 f(0.5)=0.53+3×0.5-1>0.625>0,
所以 f(0)·f(0.5)<0,
因为 ∣0-0.5∣=0.5>0.1,
所以取区间 (0,0.5) 的中点x2= =0.25,
因为 f(0.25)=0.253+3×0.25-1≈-0.23<0,
所以 f(0.25)·f(0.5)<0,
因为 ∣0.25-0.5∣=0.5>0.1,
所以取区间 (0.25,0.5) 的中点 x3= =0.375,
因为 f(0.375)=0.3753+3×0.375-1≈0.18 >0,
所以 f(0.25)·f(0.375)<0,
因为 ∣0.25-0.375∣=0.125>0.1,
所以取区间(0.25,0.375)的中点 x4==0.31.
因为 f(0.31)=0.313+3×0.0.31-1>-0.04<0,
所以 f(0.31)·f(0.375)<0,
因为 ∣0.31-0.375∣=0.065<0.1,
又因为函数 f(x) 在区间 (0.31,0.375) 上连续,
所以方程x3+3x-1=0在区间 (0,1) 上的近似解为0.3.
2. 利用计算器,求方程lgx=1-2x的近似解 (精确到0.1).
解 令f(x)=lgx+2x-1,则 f()=lg<0, f(1)=1>0.
所以函数 f(x)=lgx+2-1在区间(,1)上存在零点,
因为 f()=lg+≈0.375,
所以函数 f(x)=lgx+2x-1在区间(, )上存在零点,
因为 f()=lg+≈0.0459,
所以函数 f(x)=lgx+2x-1在区间(, )上存在零点,
因为 f()=lg+≈-0.1249,
所以函数 f(x)=lgx+2x-1在区间(, )上存在零点,
因为 -= =0.0625<0.1,
所以可取(, )中的数作为方程的近似解,
例如0.6,因此0.6是方程 lgx=1-2x的近似解.
3. 用自己的语言叙述用二分法求方程近似解的基本步骤.
① 给定区间[a,b],验证f(a)·f(b)<0,给定精确度,
② 求区间[a,b]的中点c,
③ 若 f(c)=0,则c就是函数的零点,
若f(a)·f(c)<0,则令b=c (此时零点 x0∈(a,c)),
若f(b)·f(c)<0,则令a=c (此时零点 x0∈(c,b)),
④ 判断是否达到精确度,即若∣b-a∣<,
则得到零点近似值a或b,否则重复② - ④.
4. 用两种方法解方程 2x2=3x-1.
5. 利用计算器,求方程 x3=2x+1 的近似解(精确到0.1).
因为-0.625≈-0.6,-0.5625≈-0.6,
所以取x2=-0.6
因为1.5625 ≈ 1.6,
所以取x3 ≈ 1.6.
综上,方程x3=2x+1的近似解是 x1=1.0,x2≈-0.6,x3≈1.6.
6. 利用计算器,求方程 x-cosx=0 的近似解(精确到0.1).
解:设 f(x)=x-cosx,方程的解为x0,用计算器计算得
f(0)<0,f(1)>0 x0 ∈(0,1),
f(0.5)<0,f(1)>0 x0 ∈(0.5,1),
f(0.5)<0,f(0.75)>0 x0∈( 0.5,0.75 ),
f(0.625)<0,f(0.75)>0 x0∈(0.625,0.75),
f(0.6875)<0,f(0.75)>0 x0∈(0.6875,0.75),
f(0.71875)<0,f(0.75)>0 x0∈(0.71875 ,0.75),
f(0.734 375)<0,f(0.75)>0 x0∈(0.734 375,0.75 ),
f(0.734 375)<0,f(0.742 187 5)>0
x0∈(0.734 375,0.742 187 5)
∵ 0.734375和0.742 1875 精确到0.1 的近似值都是 0.7,
∴x≈0.7.
习题 8.1
感受·理解
1. 说明下列函数在给定的区间上存在零点:
(1) f(x)= lgx+2x-5,(1,3);
(2) f(x)= 2x+x2-7,(1,2);
(3) f(x)= x3+x-1,(0,1);
(4) f(x)= 2x+sinx-l,(0,π).
(1) f(x)= lgx+2x-5,(1,3);
(2) f(x)= 2x+x2-7,(1,2);
(3) f(x)= x3+x-1,(0,1);
(4) f(x)= 2x+sinx-l,(0,π).
2. 求证:方程 x2+x+1=0 没有实数根.
3. 设m为实数若函数 y=mx2-6x+2 的图象与x轴只有1个
公共点,求m的值.
4. 设 k 为实数,若方程 4(x2-3x) +k-3=0没有实数根,
求的取值范围.
5. 求证:方程 5x2+7x-1=0 的根一个在区间(-2,-1)
内,另一个在区间(0,1)内.
证明:设 f(x)=5x2+7x-1,则二次函数f(x)是定义域R上的连续函数,
计算 f(-2)· f(-1)=(20-14-1) ×(5-7-1)<0,
所以 f(x) 的一个零点在区间(-2,1)内,
计算 f(0)·f(1)=(0+0-1) ×(5+7-1) <0,
所以f(x)的一个零点在区间 (0,1)内;
所以方程 5x2+7x-1=0的根一个在区间(-2,-1)内,另一个在区间(0,1)内.
6. 利用计算器,求方程 x2-2x-2=0 的近似解
(精确到0.1).
解 由条件x2-2x-2=0 两个根设为 x1,x2,
则x1+x2=2,
设函数为f(x)=x2-2x-2,设函数的零点为x0,
因为 f(0)=-2<0,f(-1)=1>0,
则 x0∈(-1,0) ,
取(-1,0)的中间值-0.5,所以f(-0.5) =-0.75<0,
则f(-0.5)f(-1)<0,则 x0∈(-1,-0.5),
取 (-1,-0.5)中间值-0.75,
计算得 f(-0.75)=0.0625>0,
所以 f(-0.75)f(-0.5)<0,则 x0∈(-0.75, -0.5),
取(-0.75, -0.5)中间值-0.625,
计算得 f(-0.625)=-0.3594<0,
所以 f(-0.75)f(-0.625)<0,则x0∈(-0.75,-0.625),
取(-0.75,-0.625)中间值-0.6875,
计算得 f(-0.6875) =-0.1523<0,
所以 f(-0.75)f(-0.6875)<0,则x0∈(-0.75,-0.6875),
因为∣-0.75-(-0.6875)∣=0.0625<0.1,
则方程 x2-2x-2=0的近似解为x1≈-0.7,
同理可得方程另一个近似解为x2≈2.7,
则方程两个近似解为-0.7和2.7.
7. 用多种方法解方程 x2=3x+10.
解法1:方程 x2=3x+10可化为 x2-3x-10=0,
即 (x+2)(x-5) =0,
∴x1=-2,x2=5.
解法2:方程 x2=3x+10 可化为 x2-3x-10=0,
∴ =b2-4ac= (-3)2-4×1× (-10)
=9+40=49,
∵ x=,
x1= = = = -2,
x2= = = = 5,
∴ x1=-2,x2=5.
思考·运用
8. 设 m 为实数,若方程 7x2-(m+13)x-m-2=0 的一
个根在区间 (0,1) 内,另一个根在区间 (1,2) 内,
求 m 的取值范围.
解 设 f(x)=7x2-(m+13)x-m-2,
∵方程 7x2-(m+13)x- m-2=0的一个根在区间(0,1)内,另一个根在区间(1,2)内,
解得-4<m<-2,
∴ m的取值范围是(-4,-2).
9. 设 k 为实数,若函数 f(x)=x2-2x+k 在区间[-1,0]
上有零点,求 k 的取值范围.
解 f(x)=0等价于k=2x-x2 ,
构造函数 g(x)=2x-x2 ,x∈[-1,0],
故只需要k的范围是函数g(x)的值域,
即原函数 f(x) 在区间 [-1,0] 上有零点,
g′(x) = 2xln2-2x,g′′(x) = 2x(ln2)2-2,
显然 g′′(x) 在区间[-1,0]上单调递增,
故 g′′(x) ≤ g′′(0)=(ln2)2 - 2<0,
所以 g′(x) 在区间[-1,0]上单调递减,
g′(x)≥g′(0) = ln2>0,
所以 g(x) 在区间[-1,0] 上单调递增,g(0)=1,
g(-1)=-1=-,故g(x)∈[-,1],
即k的取值范围为[-,1].
10. 设 a 为实数,函数 f(x)=x2-ax-1,且函数 f(x) 在区
间 [-1,2] 上有唯的零点,求 a 的取值范围.
解 ∵ =(-a)2-4×(-1) =a2+4>0,
∴ 方程f(a)=0有两个不等实根.
①当 f(-1)=0时,1+a-1=a=0.
此时f(a)=x2-1.
令 f(x)=0,解得 x=-1或 x=1,
此时 f(x) 在区间[-1,2] 上有两个零点,不合题意,舍掉.
② 当f(2)=0时,4-2a-1=3-2a=0,
解得 a=,
此时 f(x)=x2-x-1.
令 f(x)=0,解得 x=-或x=2,
此时 f(x) 在区间[-1,2] 上有两个零点,不合题意,舍去.
③ 若函数 f(x) 在区间(-1,2)上有唯一的零点,
则只需 f(-1)·f(2)<0,
即a(3-2a)<0,即a(2a-3)>0,
解得 a<0 或 a>,
故a的取值范围是{x∣a<0或a>}.
11. 利用计算器,求下列方程的近似解 (精确到 0.1):
(1) lg(2x) =-x+1;
(2) 3x =x+4;
(3) 2x-cosx -1=0.
(1) lg(2x) =-x+1;
解 设函数 f(x)=lg(2x)+x-1,
则 f(0.7)=lg1.4+0.7-1≈-0.15<0,
f(0.75)=lg1.5+0.75-1≈-0.07<0,
f(0.8)=lg1.6+0.8-1≈0.004>0,
所以f(x)=lg(2x)+x-1=0,
即方程 lg(2x)=-x+1的解约为0.8.
(2) 3x =x+4;
解 设函数 f(x)=3x-x-4,
则f(-4.0)=3-4.0 +4.0-4≈0.012>0,
f(-3.95)=3-3.95+3.95-4≈-0.037<0,
f(1.55)=31.55-1.55-4≈-0.060<0,
f(1.60)=31.60 -1.60-4≈0.20>0,
所以 f(x)=3x-x-4=0,即方程 3x=x+4的两个解约为-4.0和1.6.
(3) 2x-cosx -1=0.
解 设函数 f(x) =2x-cos x -1,
则f(0.8) =1.6-cos0.8-1≈-0.10<0,
f(0.85) =1.7-cos0.85-1≈0.04>0,
所以方程 2x-cosx-1=0 的解约为0.8.
探究·拓展
12. 已知定义在 R 上的函数 y=f(x)的图象是一条不间断的
曲线,f(a)≠f(b),其中a<b,设 F(x)=f(x)-,
求证:函数 F(x) 在区间 (a,b) 上有零点.
证明:∵ f(x) 在(a,b)上不间断,
∴ F(x)=f(x) - 在 (a,b)上连续.
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
