8.2 函数与数学模型 课件(共120张PPT) 2023-2024学年高一数学苏教版(2019)必修第一册
文档属性
| 名称 | 8.2 函数与数学模型 课件(共120张PPT) 2023-2024学年高一数学苏教版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 71.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-22 23:41:48 | ||
图片预览










文档简介
(共120张PPT)
第8章
函数应用
8 . 2
函数与数学模型
函数可以刻画事物变化过程中有依赖关系的两个变量之间的关系,我们能运用函数的概念与性质有效地解决问题.
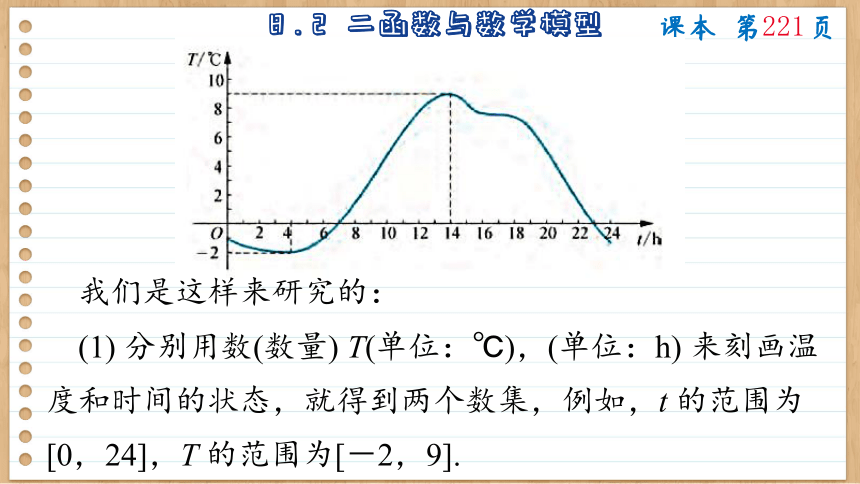
例如,要研究气温的变化规律,从气象台温度记录仪上收集到如下信息 (图 8-2-1),怎样来研究气温的变化状况呢
我们是这样来研究的:
(1) 分别用数(数量) T(单位:℃),(单位:h) 来刻画温度和时间的状态,就得到两个数集,例如,t 的范围为[0,24],T 的范围为[-2,9].
●不同的数学模型之间有什么区别
●怎样建立函数模型去解决实际问题
8.2.1
几个函数模型的比较
不同的函数模型可以刻画不同的自然现象,不同函数的“变化趋势”也不同. 对不同函数的“变化趋势”的研究和比较,可以加深我们对自然现象的理解.
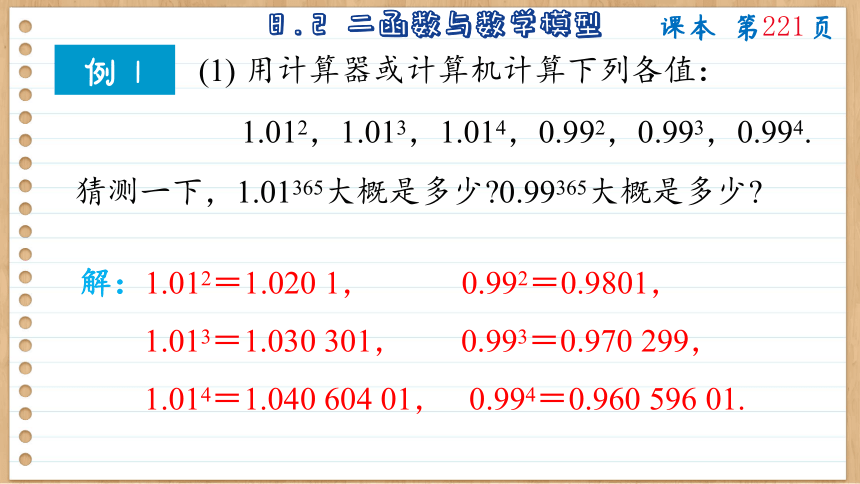
例 1
(1) 用计算器或计算机计算下列各值:
1.012,1.013,1.014,0.992,0.993,0.994.
解:1.012=1.020 1, 0.992=0.9801,
1.013=1.030 301, 0.993=0.970 299,
1.014=1.040 604 01, 0.994=0.960 596 01.
猜测一下,1.01365大概是多少 0.99365大概是多少
(2) 用计算器或计算机计算下列各值:
1.12,1.13,1.14,0.9,0.92,0.94.
猜测一下,1.1100大概是多少 1.1260大概是多少
猜测一下,0.9100大概是多少 0.91000大概是多少
解:1.12=1.21, 0.92=0.81,
1.013=1.030 301, 0.993=0.970 299,
1.014=1.040 604 01, 0.994=0.960 596 01.
(3) 用计算器或计算机计算一下(1)(2)中的结果,与你的猜测进行比较,谈谈你对“指数爆炸”的理解.
解:1.01365≈37.8, 0.99365≈0.03,
1.1100≈13 781, 0.9100≈2.656×10-5,
1.1260≈57 822 669 934,
0.91000≈1.748×10 -46.
一、“指数爆炸”的含义:
指数函数 y=ax(a>0且a≠1)随着x的增大
a>1时 y______,且增大的速度越来越_____,呈“______”的趋势
0<a<1时 y_______,并逐步趋向于______
增大
快
爆炸
减小
0
例 2
(1) 在同一个直角坐标系中画出下列 4 个函数在区间(0,+∞) 上的图象:
y=2x,y=x2,y=x0.5,y= log2x.
结合这 4 个函数的图象,比较它们随着 x 的增大函数值增长的快慢,并指出:当x 的值足够大(x>16)的时候,这4 个函数的值的大小关系;
解 这4个函数的图象如图8-2-2所示.
由图8-2-2可知:
当0<x<2时,0<x<2<4;
当x=2时,2x=x2=4;
当2<x<4时,4<2<x<16;
当x=4时,2x=x2=16;
当x>4时,16<x2<2.
对应地,当 0<x<4时,0<log2x<x0.5<2;
当x=4时,x0.5-log2x=2;
当4<x<16时,2<x0.5<log2x<4;
当x=16时,x0.5=log2x=4;
当x>16 时,x0.5>log2x.
可以发现:当 x 的值足够大(x>16)时,这 4 个函数值的大小关系是
2x>x2>x0.5>log2x.
(2) 先想象下列两组函数图象之间的关系,再用数值验算,提出更一般的猜想.
① y=1.01x与y=x100;② y=x0.25与y=lgx.
解 ①可以想象,在区间 (0,+∞) 上,函数 y=1.01x 与 y=x10 的图象都是随着 x 的增大而上升的,函数值的大小有如下特征:
当0<x<1时,1.01x>x10;
当2≤x≤9000时,1.01x<x10,
例如,当 x=9 000时,
1.019000 ≈7.8×1038,9 00010≈3.5×1039,
显然 1.019000 <9 00010;
当 x ≥ 10 000 时,1.01x>x10,
例如,当x=10000时,
1.0110000≈1.6×1043,10 00010 ≈ 1040,
显然 1.0110000 > 10 00010.
②可以想象,在区间 (0, +∞) 上,函数 y=x与y=lgx的图象都是随着x 的增大而上升的,函数值的大小有如下特征:
当0<x<10时,x0.1>1>lg x;
当30≤x<1010时,x0.1<lgx,
例如,当x=30时,300.1≈1.405 1,lg 30≈1.477 1,
显然 300.1 < lg 30;
当 x=10 时,x0.1=lgx=10;
当 x>10 时,x0.1>lg x,
例如,当x=1011 时,(1011)0.1≈12.59,lg1011≈11,
显然(1011)0.1>lg1011.
因此,我们可以得到更一般的猜想:
对于指数函数 y=a (a>1),幂函数 y=xa(a>0)和对数函数y=logax (a>1),当x足够大时,总有
ax>xa>logax.
(3) 借助图形计算器或计算机,作出下列两组函数的图象,验证你在(2)中的猜想.
① y=2x与y=x100;②y=x0.25与y=log2x.
解 借助图形计算器或计算机,观察函数 y=2x,y=x100 的图象(图 8-2-3),可以发现:当x的值从 0 开始增大时,随着 x 的增大,当0≤x≤1时,2x>x100;之后很快有 2x<x100,直到 x>997 时,总有2x>x100.
同样,借助图形计算器或计算机,观察函数 y=x0.25,y=log2x 的图象(图8-2-4),可以发现:当从4 开始增大时,一直有x0.25<log2x,直到x>65536时,总有 x0.25>log2x.
由此,我们进一步验证了(2) 中的猜想:当 足够大时,总有
ax>xa>logax.
二、三种函数的增长速度的比较
对于指数函数 y=ax(a>1),幂函数 y=xα (α>0) 和对数函数 y=logax (a>1),当 x 足够大时,总有_______________.
ax>xα>logax
(1)本质:
通过数据运算、图象的变化归纳出三种函数的增长特点和增长速度的差异.
(2)应用:
根据现实的增长情况,选择合适的函数模型刻画其变化规律.
【思考】
在三种函数增长关系的结论中,怎样理解“总会存在一个x0”
提示:因为三种函数增长速度不同,当自变量逐渐增大时,三种函数以不同的速度增加. 使函数值相等的值可视为临界点就是x0,因此可以理解为自变量足够大时一定会出现x0.当然x0不唯一,比x0大的任意一个实数也可以作为x0.
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 函数 y=log x 的衰减速度越来越慢. ( )
(2) 增长速度不变的函数模型是一次函数模型. ( )
(3) 对应任意 x∈(0,+∞),总有2x>x2. ( )
【基础小测】
2. 小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间后,为了赶时间加快速度行驶. 与以上事件吻合得最好的图象是 ( )
C
解析:小明匀速运动时,所得图象为一条直线,且距离学校越来越近,故排除A.因交通堵塞停留了一段时间,与学校的距离不变,故排除D.后来为了赶时间加快速度行驶,故排除B.
解析
3. 有一组实验数据如表所示:
x 1 2 3 4 5
y 1.5 5.9 13.4 24.1 37
下列所给函数模型较适合的是 ( )
A. y=logax (a>1) B. y=ax+b (a>1)
C. y=ax2+b (a>0) D. y=a+b(a>0)
C
解析:通过所给数据可知y随x增大,其增长速度越来越快,而A,D中的函数增长速度越来越慢,B中的函数增长速度保持不变.
解析
【跟踪训练】
1. 下列函数中,随x的增大,增长速度最快的是 ( )
A. y=100 B. y=100x
C. y=1.01x D. y=log2x
C
解析:结合函数 y=100,y=100x,y=1.01x及 y=log2x 的图象可知,随着x的增大,增长速度最快的是 y=1.01x.
解析
2. 如图,点M为 ABCD的边AB上一动点,过点M作直线l垂直于AB,且直线l与 ABCD的另一边交于点N. 当点M从A→B匀速运动时,设点M的运动
时间为t,△AMN的面积为S,能大致
反映S与t的函数关系的图象是( )
C
解析
解析 假设∠A=45°,AD=2,AB=4,点M的速度为1,则当0≤t≤2时,
AM=MN=t,则 S=t2,为二次函数;当2≤t≤4时,S=t,为一次函数.
3. 三个变量 y1,y2,y3 随着变量x的变化情况如表:
x 1 3 5 7 9 11
y1 5 135 625 1 715 3 645 6 655
y2 5 29 245 2 189 19 685 177 149
y3 5 6.10 6.61 6.985 7.2 7.4
则关于x分别呈对数函数、指数函数、幂函数变化的变量依次为 ( )
A. y1,y2,y3 B. y2,y1,y3 C.y3,y2,y1 D.y1,y3,y2
C
解析
解析 通过指数函数、对数函数、幂函数等不同函数模型的增长规律比较可知,对数函数的增长速度越来越慢,y3随x的变化符合此规律;指数函数的增长速度越来越快,y2随x的变化符合此规律;幂函数的增长速度介于指数函数与对数函数之间,y1随x的变化符合此规律.
4. 函数 y=x2与函数 y=x lg x在区间 (0,+∞) 上增长较
快的一个是___________.
y=x2
解析:当x变大时,x 比 lg x 增长要快,
所以 x2 要比 x lg x 增长的要快.
解析
5. 某电脑公司六年来电脑年产量y(台)与生产时间x(年)的函数关系如图.有下列说法:
① 前三年产量增长速度越来越快;
② 前三年产量增长速度越来越慢;
③ 后三年这种产品停止生产;
④ 后三年产量保持不变.其中说法正确的是_______.(填序号)
②④
练 习
1. 利用计算器或计算机,计算下表中与 的值对应的函数
y=0.99x与 y=1.01x 的 值 (精确到 0.000 1):
x 10 20 100 365 730
y=0.99x 0.9044 0.8179 0.3660 0.0255 0.0007
y=1.01x 1.1046 1.2202 2.7048 37.7834 1427.5879
2. 利用图形计算器或计算机,在同一个直角坐标系中画出下列各组两个函数在区间 (0, +∞) 上的图象,并结合函数的图象,比较它们随着 x 的增大函数值增长的快慢,并指出当 x 的值足够大的时候,这两个函数值的大小关系.
(1) y=10x,y=x100;
(2) y=x0.6,y=log1.5x;
(3) y=1.01x,y=x2;
(4) y=x-2,y=2-x.
(1) y=10x,y=x100;
解 y=10x 红色图象,y=x100蓝色图象.
在 (0,+∞) 上,y=10x的图象初期在 y=x100 的图象的上方,
随着x的增大图象变化到 y=x100 的图象的下方,
当x的值足够大,图象又变化到 y=x100 的图象的上方,
即相对于 y=x100来说,y=10x的图象增长的速度先快后慢,
当x的值足够大,y=10x的图象增长的速度越来越快,并远远超过 y=x100 的增长速度.
(2) y=x0.6,y=log1.5x;
解 y=x0.6 红色图象,y=log1.5x蓝色图象.
在(0,+∞)上,y=x0.6 的图象起点高,所以初期图象在 y=log1.5x 的上方,
相对于 y =log1.5x 来说,y=x0.6 的图象增长的速度先慢后快,
随着的增大,y=x0.6 的图象变化到 y=log1.5x 的图象的下方,
当x的值足够大,图象又变化到y=log1.5x的图象的上方.
解 y=1.01x 红色图象,y=x2 蓝色图象.
(3) y=1.01x,y=x2;
在(0, +∞)上,y=1.01x 的图象初期在 y 的图象的上方,随着x的增大图象变化到 y=x2 的图象的下方,
当 x 的值足够大,图象又变化到 y=x2 的图象的上方,
即相对于 y=x2 来说,y=1.01x 的图象增长的速度先快后慢,
当x的值足够大,y=1.01x 的图象增长的速度越来越快,并远远超过 y=x2 的增长速度.
(4) y=x-2,y=2-x.
解 y=x-2红色图象,y=2-x 蓝色图象.
y=x-2和 y=2-x在 (0,+∞) 上都是单调递减的函数,y=2-x的图象初期在 y=x-2 的图象的下方,
随着x的增大图象变化到y=x-2的图象的上方,
当x的值足够大,图象又变化到 y=x-2 的图象的下方,
即相对于y=x-2来说, y=2-x的图象减小的速度先慢后快,
当x的值足够大, y=2-x 的图象减小的速度越来越快,并远远超过 y=x-2 的减小速度.
8.2.2
函数的实际应用
函数是描述客观世界变化规律的基本数学模型,是研究变量之间依赖关系的有效工具. 利用函数模型可以处理生产、生活中许多实际问题.
●怎样建立函数模型,解决实际问题
●怎样选择合适的数学模型刻画客观世界的变化规律
例 3
某计算机集团公司生产某种型号计算机的固定成本为200 万元,生产每台计算机的可变成本为 3 000 元,每台计算机的售价为5 000 元.分别写出总成本 C (单位:万元)单位成本 P (单位:万元)、销售收入 R (单位:万元)以及利润 L (单位:万元)关于总产量 x (单位:台)的函数关系式.
解:总成本与总产量的关系为
C=200+0.3x,x∈N*.
单位成本与总产量的关系为
P=200x+0.3,x∈N*.
销售收入与总产量的关系为
R=0.5x,x∈N*.
利润与总产量的关系为
L=R-C=0.2x-200,x∈N*.
例 4
物体在常温下的温度变化可以用牛顿冷却规律来描述设物体的初始温度是 T0,经过一定时间 t 后的温度是T,则T-Ta= (T0-Ta)() ,其中 Ta表示环境温度,h称为半衰期. 现有一杯用 88℃ 热水冲的速溶
咖啡,放在 24 ℃的房间中,如果咖啡降温到
40℃ 需要 20 min,那么降温到 35 ℃,需要
多长时间(结果精确到0.1)
解:由题意知 40-24 = (88-24)() ,
即 = () .
解得 h = 10,故 T-24 =(88 - 24)· () ,
当T=35时,代入上式,得35-24=(88-24)·() ,
即 () =.
两边取对数,用计算器求得 t≈25.4.
因此,约需要 25.4 min 咖啡可降温到 35℃.
例 5
在经济学中,函数 f(x) 的边际函数 Mf(x) 定义为 Mf(x) = f(x+1)-f(x). 某公司每月最多生产100 台报警系统装置,生产 x 台(x∈N*) 的收入函数为 R(x)=3000x-20x (单位:元),其成本函数为 C(x)=500x+4000 (单位:元),利润是收入与成本之差.
(1) 求利润函数 P(x) 及边际利润函数 MP(x);
(2) 利润函数 P(x) 与边际利润函数 MP(x) 是否具有相同的最大值
(1) 求利润函数 P(x) 及边际利润函数 MP(x);
解 由题意知,x∈[1,100],且 x∈N*.
P(x)=R(x)-C(x)=3000x-20x2-(500x+4 000)
=-20x2+2500x-4000,
MP(x)=P(x+1)-P(x)
=-20(x+1)2+2 500(x+1) -4000-
(-20x2+2500x-4 000)
= 2 480-40x.
(2) 利润函数 P(x) 与边际利润函数 MP(x) 是否具有相同的最大值
解 P(x)=-20(x-)2+74 125,
当 x=62或 x=63 时, P(x) 的最大值为 74 120(元).
因为MP(x)=2480-40x 是减函数,
所以,当x=1时,MP(x)的最大值为 2 440(元).
因此,利润函数 P(x)与边际利润函数 MP(x)不具有相同的最大值.
例5 中边际利润函数 MP(x) 当1时取最大值,说明生产第二台与生产第一台的总利润差最大,即生产第二台报警系统装置利润最大.
MP(x)=2480-40x 是减函数,说明随着产量的增加,每台利润与前一台利润相比在减少.
通过上述 3个例子,我们可以看出,解决实际问题通常按
的程序进行,其中建立数学模型是关键.
练 习
1. 某地高山上温度从山脚起每升高 100 m 降低 0.6℃.
已知山顶的温度是14.6 ℃ ,山脚的温度是 26 ℃.
问:此山有多高
解 设从山脚起每升高x百米时,温度为y摄氏度根据题意得 y=26-0.6x,山顶温度是14.6摄氏度,代入得14.6=26-0.6x.
∴x=19 (百米),
∴山的相对高度是1900米.
2. 某车站有快、慢两种车,始发站距终点站 7.2km,慢
车到终点站需16 min,快车比慢车晚发车 3 min,且行
驶 10 min 后到达终点站. 试分别写出两车所行路程关
于慢车行驶时间的函数关系式. 两车在何时相遇 相遇
时距始发站多远
解 慢车所行路程 y1与时间 x的函数关系式为 y1 = 0.45x (0 <x≤16),
快车所行路程 y2 与慢车行驶时间 x 的函数关系式为
0,0 < x ≤ 3
y = 0.72x-3,3<x≤13,
7.2,13<x≤16
设两车在慢车出发 x min 时相遇,则 y1=y2,即 0.45x = 0.72(x-3),解得 x=8,此时y1=y2=3.6.
即两车在慢车出发 8 min 时相遇,相遇时距始发站 3.6 km.
3. 经市场调查,某商品在过去 100 天内的销售量(单位:
件) 和价格 (单位:元) 均为时间 (单位:天) 的函数,且
销售量近似地满足 g(t)=-t+ (1≤t≤100,t∈N).
前 40 天价格为 f(t)= t+22 (1≤t≤40,t∈N),后 60 天价格为 f(t)=-+52 (41≤t≤100,t∈N).试写出该种商品的日销售额 S 与时间 t 的函数关系.
解 根据题意,得 S=f(t)·g(t)=
(t+22) (-t+),(1≤t≤40),
(1≤t≤40,t∈N)
(-t+22) (-t+),(41≤t≤100),
(1≤t≤40,t∈N)
-(t2-21t-9592),(1 ≤ t ≤ 40,t∈N).
化简得 S=
(t2-213t-11336),(41≤t≤100,t∈N).
4. 某店从水果批发市场购得椰子两筐,连同运费总共花了 300 元,回来后发现有 12 个是坏的,不能将它们出售,余下的椰子按每个高出成本价 1元售出售完后共赚得 78 元. 问:这两椰子原来共有多少个
解 设这两筐椰子原来共有x个,则每个椰子的成本价为元,销售价格为+1元,销售量为(x-12)个,
根据题意有[()+1](x-12) -300 =78,即300 - - 12-300 =78
化简整理得 x2-90x-3600=0,
解得 x1=120,x2=30(不合题意,舍去)
故这两筐椰子原来共有120个.
5. 已知镭经过 100 年剩留原来的 95.76%,设质量为1的镭经过年后的剩留量为y,则 x,y的函数关系是怎样的 试写出.
解 设镭的年衰减率为r,镭开始的质量为1,
则一年后镭的剩留量为:1-1×r=1-r,
二年后镭的剩留量为:(1-r)-(1-r)r=(1-r)2,
三年后镭的剩留量为: (1-r)2-(1-r)2r=(1-r)3,
······
经过 x 年后镭的剩留量为 y,
所以 y=(1-r)x,
又因为镭经过100年剩留原来的 95.76%,
所以 0.9576=(1-r)100,
所以 1-r=0.9576 ,
所以 y=(0.9576 )x=0.9576 (x∈N*).
习题 8.2
感受·理解
1. 已知某产品今年年产量是 m 件,计划以后每年的产量
比上一年增加 20%,写出 x 年后该产品的年产量 y 与
x 之间的函数关系式.
解 1年后,年产量为 y=m·(1+20%)=1.2m (件);
2年后,年产量为 y=1.2m·(1+20%)=1.22m (件);
3年后,年产量为 y=1.22m·(1+20%)=1.23m (件);
······
x年后年产量为 y=m·1.2x(件).
所以x年后该产品的年产量y与x之间的函数关系式为y=m·12x(x∈N*)
2. 销售甲、乙两种商品所得利润分别是 P (单位:万元)
和 Q (单位:万元),它们与投入资金 t (单位:万元)
的关系有经验公式 P=t,Q=. 今将 3 万元资金
投入经营甲、乙两种商品,其中对甲种商品投资(单
位:万元),试建立总利润 y(单位:万元)关于 x 的函
数关系式.
解 由题意可知,总利润 y=P+Q,
对甲种商品投资(万元),则对乙种商品投资
(3-x)(万元),
∴y=x+,其中 x∈[0,3],
即总利润y关于x的函数关系式为
y=x+, x∈[0,3].
3. 一种放射性元素,最初质量为1000g,按每年10%衰减.
(1) 写出 x 年后这种放射性元素质量 y 与 之间的函数
关系式;
(2) 求这种放射性元素的半衰期(放射性物质的质量衰
减为原来的一半所需要的时间). (精确到 0.1)
(1) 写出 x 年后这种放射性元素质量 y 与 之间的函数
关系式;
解 最初的质量为1000g,
经过1年,y=1000(1-10%) =1000×0.9,
经过2年,y=1000(1-10%)2=1000×0.92,
经过x年,y=1000(1-10%)3=1000×0.9x,
所以年x后这种放射性元素质量y与x之间的函数关系是
y=1000×0.9x,x>0.
(2) 求这种放射性元素的半衰期(放射性物质的质量衰
减为原来的一半所需要的时间). (精确到 0.1)
解 1000×0.9x=500,x>0,
两边取常用对数 xlg0.9=lg0.5,
解得 x=≈ ≈6.5(年).
即这种放射性元素的半衰期约为6.5年.
思考·运用
4. 某工厂第一季度某产品月生产量分别为 10 000 件、
12 000 件13 000 件为了估测以后每个月的产量,以这
3 个月的产量为依据,用一个函数模拟该产品的月产
量 y (单位:件) 与月份 x 的关系. 模拟函数可以选用二
次函数或函数 y=abx+c(其中a,b,c 为常数)已知4月
份的产量为13 600件,问:用以上哪个函数作为模拟
函数较好 为什么
解 选二次函数作为模拟函数时,设 f(x)=px2+qx+r (p≠ 0).
p+q+r=10000
由已知 4p+2p+r=12000,
9p+3q+r=13000
p=-500
解得 q=3500,
r=7000
故 f(x)=-500x2+3500x+7000.
f(x)=500x+3500x+7000.
f(4)=-500×4+3500×4+7000=13000(件).
选指数型函数 g(x)=abx+c(a≠0) 作为模拟函数时,
ab+c=10000
由已知 ab2+c=12000,
ab3+c=13000
a=-8000
解得 b=0.5,
c=14000
故 g(x)=-8000×0.5x+14000.
g(4)=-8000×0.54+14000=13500 (件)
经比较可知,13500件比13000件更接近于4月份的产量13600件,
故选用指数型函数 y=- 8000×0.5x+14000 作为模拟函数较好.
5. 甲、乙两家电子商店同时上市一批移动硬盘原价 800 元/个. 为了促销,甲商店推出如下优惠政策:买 1个,单价为 780 元;买 2个,单价为 760元······依此类推,每多买1个,则单价减少 20 元,但价格底线为440 元/个商店一律按原价的 75%降价促销. 某单位需购买一批该型号的移动硬盘问:选择去哪一家商店购买,才能使得花费较少
解:设单位购买x个移动硬盘,去甲、乙两商店购买花费分别为 y甲,y乙,800-20x> 440,解得 x≤18.
当1≤x≤18时,则 y=(800-20x)x;
当x>18时,y甲=440x,
(800-20x)x;(1≤x≤18),
∴ y甲=
440x,(x>18).
y乙=800×0.75x=600x,
当x=10时,y甲=y乙;
当1≤x≤10时,y甲-y乙=200x-20x2=20x(10-x)>0,
∴ y甲> y乙.
当x>10时, y甲-y乙=20x(10-x)<0,∴ y甲< y乙.
综上可知:当个数大于10个时,在甲商店买便宜;当个数小于10个时,在乙商店买便宜;当买10个时,两商店一样.
6. 某建材实验室在做陶粒混凝土强度实验中,考察每立方米混凝土的水泥用量 x (单位:kg) 对 28 天后的混凝土抗压强度 y (单位:kg/m) 的影响,测得如下数据:
试建立适当的数学模型回答以下问题:
(1) 每立方米混凝土中增加 1 kg 水泥时,可提高抗压强度多少
解:画出散点图,如图所示
由散点图可设函数解析式为y=kx+b.
取(160,58.3),(260,89.7) 代入解得
k=0.314,b=8.06,
所以近似方程为y=0.314x+8.06,
所以每立方米混凝土中增加1kg水泥时,可提高抗压强度0.314 kg/m2;
(2) 当 x=225 (kg) 时,y 的预测值是多少
解 当x=225(kg) 时,
y=0.314×225+8.06=78.71kg/m2,
即y的预测值是78.71kg/m2.
7. 某公司今年头 6 个月的月利润如下表所示:
假定短期内利润增长基本符合对数规律,预测一下今年 7,8 两个月的月利润各是多少.
解:由题意设利润随月份增长的函数解析式为
y=klogax+b,
∵ 当x=1时,y=b=29.9,
当x=6时,y=kloga6+29.9=73.4,
∴ =43.5,
∴k= ,
故y=klogax+b=· +29.9 = +29.9,
当x=7时,y= +29.9≈77.1,
当x=8时,y= +29.9≈80.3,
所以今年7,8两个月的月利润各是77.1,80.3万元.
探究·拓展
8. (写作题) 到学校附近的农村、工厂、商店、机关作调
查,了解函数模型在生产生活中的应用,收集一些生
活中的函数模型 (指数函数、对数函数幂函数分段函
数等) 实例,并做出分析,写成调查报告.
解 我国现有人口约13亿.如果今后能将人口平均增长率控制在1%,x为年份,y(亿)为人口数.
指数函数:那么经过20年后,我国人口最多为多少亿
y=13×(1+1%)x=13×1.01x,
当 x=20 时,y=13×1.0120 ≈16(亿).
对数函数:那么经过几年后,我国人口将达到18亿
x=log1.01() = ≈33(年).
幂函数:我国现有人口约13亿,经过20年后,我国人口将达到16亿,求今后每年人口平均增长率 a 应控制在多少
y=13(1-a)x即(1+a)20=,解得 a≈1%,
分段函数:某城市出租汽车收费标准为:当行程不超过3km时,收费7元;行程超过3km,但不超过10km时,在收费7元的基础上,超过3km的部分每公里收费1.0元,不足1km的按1km算;超过10km时,超过部分除每公里收费1.0元外,再加收50%的回程空驶费,求车费 y (元) 与路程 x (km) 之间的函数解析式
设 z 为大于等于 x 的最小整数,则由题意得:
7,(0<x≤3)
y= 7+(z-3),(3<x≤10)
7+(10-3)+1.5(z-10),(x>10),
7,(0<x≤3)
即 y= 4+z,(3<x≤10)
1.5z-1,(x>10),
应用与建模
体重与脉搏
问题 生物学家认为,睡眠中的恒温动物依然会消耗体内能量,主要是为了保持体温.研究表明,消耗的能量 E 与通过心脏的血流量Q成正比. 根据生物学常识知道,动物的体重与体积成正比,表1给出了一些动物体重与脉搏率对应的数据.
(1) 根据生物学常识,给出血流量与体重之间关系的数学模型;
(2) 建立脉搏率与体重关系的数学模型;
(3) 根据表 1,作出动物的体重和脉搏率的散点图,验证所建立的数学模型.
简化假设 为了建立数学模型,需要了解一些生物学概念,例如,血流量 Q 是单位时间流过的血量,脉博率 f 是单位时间心跳的次数;还需要知道一些生物学假设,例如,心脏每次收缩挤压出来的血量 q 与心脏大小成正比,动物心脏的大小与这个动物体积的大小成正比.
建立模型 (1) 因为动物体温通过身体表面散发热量,表面积越大,散发的热量越多,保持体温需要的能量也就越大,所以动物体内消耗的能量 E 与身体的表面积 S 成正比,即 E=p1S.
又因为动物体内消耗的能量 E 与通过心脏的血流量 Q 成正比,即 E=p2Q. 由此可得 Q=S,其中 p1,p2 和 p为均为正的比例系数.
另一方面,体积 V 与体重 W 成正比,即 V=r1W.
又因为表面积 S 大约与体积 V 的 次方成正比,即 S= r2V . 由此可得 S=rW ,其中r1,r2,r 为正的比例系数.
因此,血流量与体重关系的数学模型为
Q=k1W ,
其中 k1 为正的比例系数.
(2)根据脉搏率的定义 f=,再根据生物学假设 q=cW (c为正的比例系数),可得 f= =. 因此,脉搏率与体重关系的数学模型为
f=kW ,
其中k为正的待定系数.
-
(3) 我们用 Excel作出数据的散点图:在工作表中输入数据,选中数据区,按“插入/图表/散点图”的顺序作出散点图(图 1).
右击数据点,选择“添加趋势线”,在 6 种类型中分别选择指数幂、二次多项式等趋势线,根据显示的“R平方值”,选择最大的一个.
因此,采用幂函数模型,在“选项”中选定“显示公式”和“显示 R平方值”复选框,得到图 2.
可以看出,得到的拟合模型 f=1790.9 W-0.298 与(2)中建立的数学模型接近.
回顾与评价
(1) 脉搏率与体重关系的数学模型说明,恒温动物体重越大,脉搏率越低;脉搏率与体重的 次方成反比.
表 1中的数据基本上反映了这个关系.
(2) 当所给的数据差异较大时,可以对已知数据取对数,从而使变换后的数据变得“均匀”,有利于发现趋势或规律.
本例中将体重 W 与脉搏率分别取自然对数后作出的散点图如图 3 所示. 直观地看出,变换后的数据点分布均匀,并近似地在一条直线上.
(3) 数据拟合是研究变量之间的关系,并给出近似数学表达式的一种方法. 根据拟合模型,我们还可以对某变量进行预测或控制. 在解决数据拟合问题时,首先应作出数据的散点图,然后通过观察散点的趋势选用相应的模型进行拟合. 为使散点图更清晰,可将数据适当简化或变换.
练 习
下表给出了八大行星与冥王星离太阳的距离和它们运行的周期,试建立这两组数据之间的关系.
解:在Excel表格中作出散点图,添加趋势线显示公式(模拟函数),
一次函数模型为 y=14.928x-4584.3,二次函数模型为 y=0.0015x2+6.410 9x-799.11.
阅 读
G大调的正弦函数
音乐,是人类精神通过无意识计算而获得的愉悦享受.
——G莱布尼茨
传说毕达哥拉斯很喜欢弹古希腊的七弦琴,他发现,当弦的粗细不变时,拨弄弦弹出的声音音高取决于各弦的长度,当弦的长度成简单的整数比时,它就发出和谐的声音.
从那时起,音乐的研究与数学连成了一体,数学家和音乐家都试图弄清音乐声音的本质,扩大音乐与数学两者之间的联系.
先考虑由音叉发出的简单的声音.
数学家研究发现,音叉发出的声音(音叉附近空气分子的振动)可以用函数模型 y=Asin ωt (A>0>0)来刻画,这是一个周期函数,最小正周期为.
有些声音悦耳动听,有些声音则叫人无法忍受. 同一个音符,为什么小提琴和钢琴发出的声音传到耳朵里会有不同的效果呢 观察发现,所有声音的图象都呈现周期性.
我们可以用小提琴和单簧管的声音图象加以证实,也可以用 father 一词中a 的声音的图象来证实,如图1所示.
如图 1所示的这种具有周期性的声音,在整体上来说是悦耳的称为音乐声音.
1807年,法国著名数学家傅里叶 (Fourier.1768-1830) 用一个幼粹的数学定理表述了这种规则特征:代表任何周期性声音的公式是形如 Asinωt 的简单正弦函数之和,而且这些正弦函数的频率都是其中一个最小频率的整数倍. 比如说图1中的小提琴的声音图象公式基本上是
y=0.06sin1000πt-0.02sin2 000πt-0.0lsin3 000πt.
首先,这个公式是简单的正弦表达式之和:其次,第 1项的频率是500,第2项的频率是1000,第3项的频率是1500. 因此,第2项和第3项的频率是最低频率的整数倍,这些简单三角函数的图象如图 2 所示.
例如,一个音质与上面的小提琴音质完全相同的声音,能够由 3个具有适当相关音量的、每个频率分别为 500,1 000,1500 的音叉同时发声而产生.因此,从理论上来讲,完全可以由音叉来演奏贝多芬第九交响曲.
通过傅里叶定理,我们明白了一般的音乐声音的数学特征:各种声音都可以归于一些简单声音的基本组合,而这些简单声音在数学上又不会比简单的三角函数更复杂.
上面简单的描述表明,数学已经深深地渗入到音乐领域中了
本课结束
This lesson is over
THANKS!
第8章
函数应用
8 . 2
函数与数学模型
函数可以刻画事物变化过程中有依赖关系的两个变量之间的关系,我们能运用函数的概念与性质有效地解决问题.
例如,要研究气温的变化规律,从气象台温度记录仪上收集到如下信息 (图 8-2-1),怎样来研究气温的变化状况呢
我们是这样来研究的:
(1) 分别用数(数量) T(单位:℃),(单位:h) 来刻画温度和时间的状态,就得到两个数集,例如,t 的范围为[0,24],T 的范围为[-2,9].
●不同的数学模型之间有什么区别
●怎样建立函数模型去解决实际问题
8.2.1
几个函数模型的比较
不同的函数模型可以刻画不同的自然现象,不同函数的“变化趋势”也不同. 对不同函数的“变化趋势”的研究和比较,可以加深我们对自然现象的理解.
例 1
(1) 用计算器或计算机计算下列各值:
1.012,1.013,1.014,0.992,0.993,0.994.
解:1.012=1.020 1, 0.992=0.9801,
1.013=1.030 301, 0.993=0.970 299,
1.014=1.040 604 01, 0.994=0.960 596 01.
猜测一下,1.01365大概是多少 0.99365大概是多少
(2) 用计算器或计算机计算下列各值:
1.12,1.13,1.14,0.9,0.92,0.94.
猜测一下,1.1100大概是多少 1.1260大概是多少
猜测一下,0.9100大概是多少 0.91000大概是多少
解:1.12=1.21, 0.92=0.81,
1.013=1.030 301, 0.993=0.970 299,
1.014=1.040 604 01, 0.994=0.960 596 01.
(3) 用计算器或计算机计算一下(1)(2)中的结果,与你的猜测进行比较,谈谈你对“指数爆炸”的理解.
解:1.01365≈37.8, 0.99365≈0.03,
1.1100≈13 781, 0.9100≈2.656×10-5,
1.1260≈57 822 669 934,
0.91000≈1.748×10 -46.
一、“指数爆炸”的含义:
指数函数 y=ax(a>0且a≠1)随着x的增大
a>1时 y______,且增大的速度越来越_____,呈“______”的趋势
0<a<1时 y_______,并逐步趋向于______
增大
快
爆炸
减小
0
例 2
(1) 在同一个直角坐标系中画出下列 4 个函数在区间(0,+∞) 上的图象:
y=2x,y=x2,y=x0.5,y= log2x.
结合这 4 个函数的图象,比较它们随着 x 的增大函数值增长的快慢,并指出:当x 的值足够大(x>16)的时候,这4 个函数的值的大小关系;
解 这4个函数的图象如图8-2-2所示.
由图8-2-2可知:
当0<x<2时,0<x<2<4;
当x=2时,2x=x2=4;
当2<x<4时,4<2<x<16;
当x=4时,2x=x2=16;
当x>4时,16<x2<2.
对应地,当 0<x<4时,0<log2x<x0.5<2;
当x=4时,x0.5-log2x=2;
当4<x<16时,2<x0.5<log2x<4;
当x=16时,x0.5=log2x=4;
当x>16 时,x0.5>log2x.
可以发现:当 x 的值足够大(x>16)时,这 4 个函数值的大小关系是
2x>x2>x0.5>log2x.
(2) 先想象下列两组函数图象之间的关系,再用数值验算,提出更一般的猜想.
① y=1.01x与y=x100;② y=x0.25与y=lgx.
解 ①可以想象,在区间 (0,+∞) 上,函数 y=1.01x 与 y=x10 的图象都是随着 x 的增大而上升的,函数值的大小有如下特征:
当0<x<1时,1.01x>x10;
当2≤x≤9000时,1.01x<x10,
例如,当 x=9 000时,
1.019000 ≈7.8×1038,9 00010≈3.5×1039,
显然 1.019000 <9 00010;
当 x ≥ 10 000 时,1.01x>x10,
例如,当x=10000时,
1.0110000≈1.6×1043,10 00010 ≈ 1040,
显然 1.0110000 > 10 00010.
②可以想象,在区间 (0, +∞) 上,函数 y=x与y=lgx的图象都是随着x 的增大而上升的,函数值的大小有如下特征:
当0<x<10时,x0.1>1>lg x;
当30≤x<1010时,x0.1<lgx,
例如,当x=30时,300.1≈1.405 1,lg 30≈1.477 1,
显然 300.1 < lg 30;
当 x=10 时,x0.1=lgx=10;
当 x>10 时,x0.1>lg x,
例如,当x=1011 时,(1011)0.1≈12.59,lg1011≈11,
显然(1011)0.1>lg1011.
因此,我们可以得到更一般的猜想:
对于指数函数 y=a (a>1),幂函数 y=xa(a>0)和对数函数y=logax (a>1),当x足够大时,总有
ax>xa>logax.
(3) 借助图形计算器或计算机,作出下列两组函数的图象,验证你在(2)中的猜想.
① y=2x与y=x100;②y=x0.25与y=log2x.
解 借助图形计算器或计算机,观察函数 y=2x,y=x100 的图象(图 8-2-3),可以发现:当x的值从 0 开始增大时,随着 x 的增大,当0≤x≤1时,2x>x100;之后很快有 2x<x100,直到 x>997 时,总有2x>x100.
同样,借助图形计算器或计算机,观察函数 y=x0.25,y=log2x 的图象(图8-2-4),可以发现:当从4 开始增大时,一直有x0.25<log2x,直到x>65536时,总有 x0.25>log2x.
由此,我们进一步验证了(2) 中的猜想:当 足够大时,总有
ax>xa>logax.
二、三种函数的增长速度的比较
对于指数函数 y=ax(a>1),幂函数 y=xα (α>0) 和对数函数 y=logax (a>1),当 x 足够大时,总有_______________.
ax>xα>logax
(1)本质:
通过数据运算、图象的变化归纳出三种函数的增长特点和增长速度的差异.
(2)应用:
根据现实的增长情况,选择合适的函数模型刻画其变化规律.
【思考】
在三种函数增长关系的结论中,怎样理解“总会存在一个x0”
提示:因为三种函数增长速度不同,当自变量逐渐增大时,三种函数以不同的速度增加. 使函数值相等的值可视为临界点就是x0,因此可以理解为自变量足够大时一定会出现x0.当然x0不唯一,比x0大的任意一个实数也可以作为x0.
1. 辨析记忆(对的打“ ”,错的打“ ”)
(1) 函数 y=log x 的衰减速度越来越慢. ( )
(2) 增长速度不变的函数模型是一次函数模型. ( )
(3) 对应任意 x∈(0,+∞),总有2x>x2. ( )
【基础小测】
2. 小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间后,为了赶时间加快速度行驶. 与以上事件吻合得最好的图象是 ( )
C
解析:小明匀速运动时,所得图象为一条直线,且距离学校越来越近,故排除A.因交通堵塞停留了一段时间,与学校的距离不变,故排除D.后来为了赶时间加快速度行驶,故排除B.
解析
3. 有一组实验数据如表所示:
x 1 2 3 4 5
y 1.5 5.9 13.4 24.1 37
下列所给函数模型较适合的是 ( )
A. y=logax (a>1) B. y=ax+b (a>1)
C. y=ax2+b (a>0) D. y=a+b(a>0)
C
解析:通过所给数据可知y随x增大,其增长速度越来越快,而A,D中的函数增长速度越来越慢,B中的函数增长速度保持不变.
解析
【跟踪训练】
1. 下列函数中,随x的增大,增长速度最快的是 ( )
A. y=100 B. y=100x
C. y=1.01x D. y=log2x
C
解析:结合函数 y=100,y=100x,y=1.01x及 y=log2x 的图象可知,随着x的增大,增长速度最快的是 y=1.01x.
解析
2. 如图,点M为 ABCD的边AB上一动点,过点M作直线l垂直于AB,且直线l与 ABCD的另一边交于点N. 当点M从A→B匀速运动时,设点M的运动
时间为t,△AMN的面积为S,能大致
反映S与t的函数关系的图象是( )
C
解析
解析 假设∠A=45°,AD=2,AB=4,点M的速度为1,则当0≤t≤2时,
AM=MN=t,则 S=t2,为二次函数;当2≤t≤4时,S=t,为一次函数.
3. 三个变量 y1,y2,y3 随着变量x的变化情况如表:
x 1 3 5 7 9 11
y1 5 135 625 1 715 3 645 6 655
y2 5 29 245 2 189 19 685 177 149
y3 5 6.10 6.61 6.985 7.2 7.4
则关于x分别呈对数函数、指数函数、幂函数变化的变量依次为 ( )
A. y1,y2,y3 B. y2,y1,y3 C.y3,y2,y1 D.y1,y3,y2
C
解析
解析 通过指数函数、对数函数、幂函数等不同函数模型的增长规律比较可知,对数函数的增长速度越来越慢,y3随x的变化符合此规律;指数函数的增长速度越来越快,y2随x的变化符合此规律;幂函数的增长速度介于指数函数与对数函数之间,y1随x的变化符合此规律.
4. 函数 y=x2与函数 y=x lg x在区间 (0,+∞) 上增长较
快的一个是___________.
y=x2
解析:当x变大时,x 比 lg x 增长要快,
所以 x2 要比 x lg x 增长的要快.
解析
5. 某电脑公司六年来电脑年产量y(台)与生产时间x(年)的函数关系如图.有下列说法:
① 前三年产量增长速度越来越快;
② 前三年产量增长速度越来越慢;
③ 后三年这种产品停止生产;
④ 后三年产量保持不变.其中说法正确的是_______.(填序号)
②④
练 习
1. 利用计算器或计算机,计算下表中与 的值对应的函数
y=0.99x与 y=1.01x 的 值 (精确到 0.000 1):
x 10 20 100 365 730
y=0.99x 0.9044 0.8179 0.3660 0.0255 0.0007
y=1.01x 1.1046 1.2202 2.7048 37.7834 1427.5879
2. 利用图形计算器或计算机,在同一个直角坐标系中画出下列各组两个函数在区间 (0, +∞) 上的图象,并结合函数的图象,比较它们随着 x 的增大函数值增长的快慢,并指出当 x 的值足够大的时候,这两个函数值的大小关系.
(1) y=10x,y=x100;
(2) y=x0.6,y=log1.5x;
(3) y=1.01x,y=x2;
(4) y=x-2,y=2-x.
(1) y=10x,y=x100;
解 y=10x 红色图象,y=x100蓝色图象.
在 (0,+∞) 上,y=10x的图象初期在 y=x100 的图象的上方,
随着x的增大图象变化到 y=x100 的图象的下方,
当x的值足够大,图象又变化到 y=x100 的图象的上方,
即相对于 y=x100来说,y=10x的图象增长的速度先快后慢,
当x的值足够大,y=10x的图象增长的速度越来越快,并远远超过 y=x100 的增长速度.
(2) y=x0.6,y=log1.5x;
解 y=x0.6 红色图象,y=log1.5x蓝色图象.
在(0,+∞)上,y=x0.6 的图象起点高,所以初期图象在 y=log1.5x 的上方,
相对于 y =log1.5x 来说,y=x0.6 的图象增长的速度先慢后快,
随着的增大,y=x0.6 的图象变化到 y=log1.5x 的图象的下方,
当x的值足够大,图象又变化到y=log1.5x的图象的上方.
解 y=1.01x 红色图象,y=x2 蓝色图象.
(3) y=1.01x,y=x2;
在(0, +∞)上,y=1.01x 的图象初期在 y 的图象的上方,随着x的增大图象变化到 y=x2 的图象的下方,
当 x 的值足够大,图象又变化到 y=x2 的图象的上方,
即相对于 y=x2 来说,y=1.01x 的图象增长的速度先快后慢,
当x的值足够大,y=1.01x 的图象增长的速度越来越快,并远远超过 y=x2 的增长速度.
(4) y=x-2,y=2-x.
解 y=x-2红色图象,y=2-x 蓝色图象.
y=x-2和 y=2-x在 (0,+∞) 上都是单调递减的函数,y=2-x的图象初期在 y=x-2 的图象的下方,
随着x的增大图象变化到y=x-2的图象的上方,
当x的值足够大,图象又变化到 y=x-2 的图象的下方,
即相对于y=x-2来说, y=2-x的图象减小的速度先慢后快,
当x的值足够大, y=2-x 的图象减小的速度越来越快,并远远超过 y=x-2 的减小速度.
8.2.2
函数的实际应用
函数是描述客观世界变化规律的基本数学模型,是研究变量之间依赖关系的有效工具. 利用函数模型可以处理生产、生活中许多实际问题.
●怎样建立函数模型,解决实际问题
●怎样选择合适的数学模型刻画客观世界的变化规律
例 3
某计算机集团公司生产某种型号计算机的固定成本为200 万元,生产每台计算机的可变成本为 3 000 元,每台计算机的售价为5 000 元.分别写出总成本 C (单位:万元)单位成本 P (单位:万元)、销售收入 R (单位:万元)以及利润 L (单位:万元)关于总产量 x (单位:台)的函数关系式.
解:总成本与总产量的关系为
C=200+0.3x,x∈N*.
单位成本与总产量的关系为
P=200x+0.3,x∈N*.
销售收入与总产量的关系为
R=0.5x,x∈N*.
利润与总产量的关系为
L=R-C=0.2x-200,x∈N*.
例 4
物体在常温下的温度变化可以用牛顿冷却规律来描述设物体的初始温度是 T0,经过一定时间 t 后的温度是T,则T-Ta= (T0-Ta)() ,其中 Ta表示环境温度,h称为半衰期. 现有一杯用 88℃ 热水冲的速溶
咖啡,放在 24 ℃的房间中,如果咖啡降温到
40℃ 需要 20 min,那么降温到 35 ℃,需要
多长时间(结果精确到0.1)
解:由题意知 40-24 = (88-24)() ,
即 = () .
解得 h = 10,故 T-24 =(88 - 24)· () ,
当T=35时,代入上式,得35-24=(88-24)·() ,
即 () =.
两边取对数,用计算器求得 t≈25.4.
因此,约需要 25.4 min 咖啡可降温到 35℃.
例 5
在经济学中,函数 f(x) 的边际函数 Mf(x) 定义为 Mf(x) = f(x+1)-f(x). 某公司每月最多生产100 台报警系统装置,生产 x 台(x∈N*) 的收入函数为 R(x)=3000x-20x (单位:元),其成本函数为 C(x)=500x+4000 (单位:元),利润是收入与成本之差.
(1) 求利润函数 P(x) 及边际利润函数 MP(x);
(2) 利润函数 P(x) 与边际利润函数 MP(x) 是否具有相同的最大值
(1) 求利润函数 P(x) 及边际利润函数 MP(x);
解 由题意知,x∈[1,100],且 x∈N*.
P(x)=R(x)-C(x)=3000x-20x2-(500x+4 000)
=-20x2+2500x-4000,
MP(x)=P(x+1)-P(x)
=-20(x+1)2+2 500(x+1) -4000-
(-20x2+2500x-4 000)
= 2 480-40x.
(2) 利润函数 P(x) 与边际利润函数 MP(x) 是否具有相同的最大值
解 P(x)=-20(x-)2+74 125,
当 x=62或 x=63 时, P(x) 的最大值为 74 120(元).
因为MP(x)=2480-40x 是减函数,
所以,当x=1时,MP(x)的最大值为 2 440(元).
因此,利润函数 P(x)与边际利润函数 MP(x)不具有相同的最大值.
例5 中边际利润函数 MP(x) 当1时取最大值,说明生产第二台与生产第一台的总利润差最大,即生产第二台报警系统装置利润最大.
MP(x)=2480-40x 是减函数,说明随着产量的增加,每台利润与前一台利润相比在减少.
通过上述 3个例子,我们可以看出,解决实际问题通常按
的程序进行,其中建立数学模型是关键.
练 习
1. 某地高山上温度从山脚起每升高 100 m 降低 0.6℃.
已知山顶的温度是14.6 ℃ ,山脚的温度是 26 ℃.
问:此山有多高
解 设从山脚起每升高x百米时,温度为y摄氏度根据题意得 y=26-0.6x,山顶温度是14.6摄氏度,代入得14.6=26-0.6x.
∴x=19 (百米),
∴山的相对高度是1900米.
2. 某车站有快、慢两种车,始发站距终点站 7.2km,慢
车到终点站需16 min,快车比慢车晚发车 3 min,且行
驶 10 min 后到达终点站. 试分别写出两车所行路程关
于慢车行驶时间的函数关系式. 两车在何时相遇 相遇
时距始发站多远
解 慢车所行路程 y1与时间 x的函数关系式为 y1 = 0.45x (0 <x≤16),
快车所行路程 y2 与慢车行驶时间 x 的函数关系式为
0,0 < x ≤ 3
y = 0.72x-3,3<x≤13,
7.2,13<x≤16
设两车在慢车出发 x min 时相遇,则 y1=y2,即 0.45x = 0.72(x-3),解得 x=8,此时y1=y2=3.6.
即两车在慢车出发 8 min 时相遇,相遇时距始发站 3.6 km.
3. 经市场调查,某商品在过去 100 天内的销售量(单位:
件) 和价格 (单位:元) 均为时间 (单位:天) 的函数,且
销售量近似地满足 g(t)=-t+ (1≤t≤100,t∈N).
前 40 天价格为 f(t)= t+22 (1≤t≤40,t∈N),后 60 天价格为 f(t)=-+52 (41≤t≤100,t∈N).试写出该种商品的日销售额 S 与时间 t 的函数关系.
解 根据题意,得 S=f(t)·g(t)=
(t+22) (-t+),(1≤t≤40),
(1≤t≤40,t∈N)
(-t+22) (-t+),(41≤t≤100),
(1≤t≤40,t∈N)
-(t2-21t-9592),(1 ≤ t ≤ 40,t∈N).
化简得 S=
(t2-213t-11336),(41≤t≤100,t∈N).
4. 某店从水果批发市场购得椰子两筐,连同运费总共花了 300 元,回来后发现有 12 个是坏的,不能将它们出售,余下的椰子按每个高出成本价 1元售出售完后共赚得 78 元. 问:这两椰子原来共有多少个
解 设这两筐椰子原来共有x个,则每个椰子的成本价为元,销售价格为+1元,销售量为(x-12)个,
根据题意有[()+1](x-12) -300 =78,即300 - - 12-300 =78
化简整理得 x2-90x-3600=0,
解得 x1=120,x2=30(不合题意,舍去)
故这两筐椰子原来共有120个.
5. 已知镭经过 100 年剩留原来的 95.76%,设质量为1的镭经过年后的剩留量为y,则 x,y的函数关系是怎样的 试写出.
解 设镭的年衰减率为r,镭开始的质量为1,
则一年后镭的剩留量为:1-1×r=1-r,
二年后镭的剩留量为:(1-r)-(1-r)r=(1-r)2,
三年后镭的剩留量为: (1-r)2-(1-r)2r=(1-r)3,
······
经过 x 年后镭的剩留量为 y,
所以 y=(1-r)x,
又因为镭经过100年剩留原来的 95.76%,
所以 0.9576=(1-r)100,
所以 1-r=0.9576 ,
所以 y=(0.9576 )x=0.9576 (x∈N*).
习题 8.2
感受·理解
1. 已知某产品今年年产量是 m 件,计划以后每年的产量
比上一年增加 20%,写出 x 年后该产品的年产量 y 与
x 之间的函数关系式.
解 1年后,年产量为 y=m·(1+20%)=1.2m (件);
2年后,年产量为 y=1.2m·(1+20%)=1.22m (件);
3年后,年产量为 y=1.22m·(1+20%)=1.23m (件);
······
x年后年产量为 y=m·1.2x(件).
所以x年后该产品的年产量y与x之间的函数关系式为y=m·12x(x∈N*)
2. 销售甲、乙两种商品所得利润分别是 P (单位:万元)
和 Q (单位:万元),它们与投入资金 t (单位:万元)
的关系有经验公式 P=t,Q=. 今将 3 万元资金
投入经营甲、乙两种商品,其中对甲种商品投资(单
位:万元),试建立总利润 y(单位:万元)关于 x 的函
数关系式.
解 由题意可知,总利润 y=P+Q,
对甲种商品投资(万元),则对乙种商品投资
(3-x)(万元),
∴y=x+,其中 x∈[0,3],
即总利润y关于x的函数关系式为
y=x+, x∈[0,3].
3. 一种放射性元素,最初质量为1000g,按每年10%衰减.
(1) 写出 x 年后这种放射性元素质量 y 与 之间的函数
关系式;
(2) 求这种放射性元素的半衰期(放射性物质的质量衰
减为原来的一半所需要的时间). (精确到 0.1)
(1) 写出 x 年后这种放射性元素质量 y 与 之间的函数
关系式;
解 最初的质量为1000g,
经过1年,y=1000(1-10%) =1000×0.9,
经过2年,y=1000(1-10%)2=1000×0.92,
经过x年,y=1000(1-10%)3=1000×0.9x,
所以年x后这种放射性元素质量y与x之间的函数关系是
y=1000×0.9x,x>0.
(2) 求这种放射性元素的半衰期(放射性物质的质量衰
减为原来的一半所需要的时间). (精确到 0.1)
解 1000×0.9x=500,x>0,
两边取常用对数 xlg0.9=lg0.5,
解得 x=≈ ≈6.5(年).
即这种放射性元素的半衰期约为6.5年.
思考·运用
4. 某工厂第一季度某产品月生产量分别为 10 000 件、
12 000 件13 000 件为了估测以后每个月的产量,以这
3 个月的产量为依据,用一个函数模拟该产品的月产
量 y (单位:件) 与月份 x 的关系. 模拟函数可以选用二
次函数或函数 y=abx+c(其中a,b,c 为常数)已知4月
份的产量为13 600件,问:用以上哪个函数作为模拟
函数较好 为什么
解 选二次函数作为模拟函数时,设 f(x)=px2+qx+r (p≠ 0).
p+q+r=10000
由已知 4p+2p+r=12000,
9p+3q+r=13000
p=-500
解得 q=3500,
r=7000
故 f(x)=-500x2+3500x+7000.
f(x)=500x+3500x+7000.
f(4)=-500×4+3500×4+7000=13000(件).
选指数型函数 g(x)=abx+c(a≠0) 作为模拟函数时,
ab+c=10000
由已知 ab2+c=12000,
ab3+c=13000
a=-8000
解得 b=0.5,
c=14000
故 g(x)=-8000×0.5x+14000.
g(4)=-8000×0.54+14000=13500 (件)
经比较可知,13500件比13000件更接近于4月份的产量13600件,
故选用指数型函数 y=- 8000×0.5x+14000 作为模拟函数较好.
5. 甲、乙两家电子商店同时上市一批移动硬盘原价 800 元/个. 为了促销,甲商店推出如下优惠政策:买 1个,单价为 780 元;买 2个,单价为 760元······依此类推,每多买1个,则单价减少 20 元,但价格底线为440 元/个商店一律按原价的 75%降价促销. 某单位需购买一批该型号的移动硬盘问:选择去哪一家商店购买,才能使得花费较少
解:设单位购买x个移动硬盘,去甲、乙两商店购买花费分别为 y甲,y乙,800-20x> 440,解得 x≤18.
当1≤x≤18时,则 y=(800-20x)x;
当x>18时,y甲=440x,
(800-20x)x;(1≤x≤18),
∴ y甲=
440x,(x>18).
y乙=800×0.75x=600x,
当x=10时,y甲=y乙;
当1≤x≤10时,y甲-y乙=200x-20x2=20x(10-x)>0,
∴ y甲> y乙.
当x>10时, y甲-y乙=20x(10-x)<0,∴ y甲< y乙.
综上可知:当个数大于10个时,在甲商店买便宜;当个数小于10个时,在乙商店买便宜;当买10个时,两商店一样.
6. 某建材实验室在做陶粒混凝土强度实验中,考察每立方米混凝土的水泥用量 x (单位:kg) 对 28 天后的混凝土抗压强度 y (单位:kg/m) 的影响,测得如下数据:
试建立适当的数学模型回答以下问题:
(1) 每立方米混凝土中增加 1 kg 水泥时,可提高抗压强度多少
解:画出散点图,如图所示
由散点图可设函数解析式为y=kx+b.
取(160,58.3),(260,89.7) 代入解得
k=0.314,b=8.06,
所以近似方程为y=0.314x+8.06,
所以每立方米混凝土中增加1kg水泥时,可提高抗压强度0.314 kg/m2;
(2) 当 x=225 (kg) 时,y 的预测值是多少
解 当x=225(kg) 时,
y=0.314×225+8.06=78.71kg/m2,
即y的预测值是78.71kg/m2.
7. 某公司今年头 6 个月的月利润如下表所示:
假定短期内利润增长基本符合对数规律,预测一下今年 7,8 两个月的月利润各是多少.
解:由题意设利润随月份增长的函数解析式为
y=klogax+b,
∵ 当x=1时,y=b=29.9,
当x=6时,y=kloga6+29.9=73.4,
∴ =43.5,
∴k= ,
故y=klogax+b=· +29.9 = +29.9,
当x=7时,y= +29.9≈77.1,
当x=8时,y= +29.9≈80.3,
所以今年7,8两个月的月利润各是77.1,80.3万元.
探究·拓展
8. (写作题) 到学校附近的农村、工厂、商店、机关作调
查,了解函数模型在生产生活中的应用,收集一些生
活中的函数模型 (指数函数、对数函数幂函数分段函
数等) 实例,并做出分析,写成调查报告.
解 我国现有人口约13亿.如果今后能将人口平均增长率控制在1%,x为年份,y(亿)为人口数.
指数函数:那么经过20年后,我国人口最多为多少亿
y=13×(1+1%)x=13×1.01x,
当 x=20 时,y=13×1.0120 ≈16(亿).
对数函数:那么经过几年后,我国人口将达到18亿
x=log1.01() = ≈33(年).
幂函数:我国现有人口约13亿,经过20年后,我国人口将达到16亿,求今后每年人口平均增长率 a 应控制在多少
y=13(1-a)x即(1+a)20=,解得 a≈1%,
分段函数:某城市出租汽车收费标准为:当行程不超过3km时,收费7元;行程超过3km,但不超过10km时,在收费7元的基础上,超过3km的部分每公里收费1.0元,不足1km的按1km算;超过10km时,超过部分除每公里收费1.0元外,再加收50%的回程空驶费,求车费 y (元) 与路程 x (km) 之间的函数解析式
设 z 为大于等于 x 的最小整数,则由题意得:
7,(0<x≤3)
y= 7+(z-3),(3<x≤10)
7+(10-3)+1.5(z-10),(x>10),
7,(0<x≤3)
即 y= 4+z,(3<x≤10)
1.5z-1,(x>10),
应用与建模
体重与脉搏
问题 生物学家认为,睡眠中的恒温动物依然会消耗体内能量,主要是为了保持体温.研究表明,消耗的能量 E 与通过心脏的血流量Q成正比. 根据生物学常识知道,动物的体重与体积成正比,表1给出了一些动物体重与脉搏率对应的数据.
(1) 根据生物学常识,给出血流量与体重之间关系的数学模型;
(2) 建立脉搏率与体重关系的数学模型;
(3) 根据表 1,作出动物的体重和脉搏率的散点图,验证所建立的数学模型.
简化假设 为了建立数学模型,需要了解一些生物学概念,例如,血流量 Q 是单位时间流过的血量,脉博率 f 是单位时间心跳的次数;还需要知道一些生物学假设,例如,心脏每次收缩挤压出来的血量 q 与心脏大小成正比,动物心脏的大小与这个动物体积的大小成正比.
建立模型 (1) 因为动物体温通过身体表面散发热量,表面积越大,散发的热量越多,保持体温需要的能量也就越大,所以动物体内消耗的能量 E 与身体的表面积 S 成正比,即 E=p1S.
又因为动物体内消耗的能量 E 与通过心脏的血流量 Q 成正比,即 E=p2Q. 由此可得 Q=S,其中 p1,p2 和 p为均为正的比例系数.
另一方面,体积 V 与体重 W 成正比,即 V=r1W.
又因为表面积 S 大约与体积 V 的 次方成正比,即 S= r2V . 由此可得 S=rW ,其中r1,r2,r 为正的比例系数.
因此,血流量与体重关系的数学模型为
Q=k1W ,
其中 k1 为正的比例系数.
(2)根据脉搏率的定义 f=,再根据生物学假设 q=cW (c为正的比例系数),可得 f= =. 因此,脉搏率与体重关系的数学模型为
f=kW ,
其中k为正的待定系数.
-
(3) 我们用 Excel作出数据的散点图:在工作表中输入数据,选中数据区,按“插入/图表/散点图”的顺序作出散点图(图 1).
右击数据点,选择“添加趋势线”,在 6 种类型中分别选择指数幂、二次多项式等趋势线,根据显示的“R平方值”,选择最大的一个.
因此,采用幂函数模型,在“选项”中选定“显示公式”和“显示 R平方值”复选框,得到图 2.
可以看出,得到的拟合模型 f=1790.9 W-0.298 与(2)中建立的数学模型接近.
回顾与评价
(1) 脉搏率与体重关系的数学模型说明,恒温动物体重越大,脉搏率越低;脉搏率与体重的 次方成反比.
表 1中的数据基本上反映了这个关系.
(2) 当所给的数据差异较大时,可以对已知数据取对数,从而使变换后的数据变得“均匀”,有利于发现趋势或规律.
本例中将体重 W 与脉搏率分别取自然对数后作出的散点图如图 3 所示. 直观地看出,变换后的数据点分布均匀,并近似地在一条直线上.
(3) 数据拟合是研究变量之间的关系,并给出近似数学表达式的一种方法. 根据拟合模型,我们还可以对某变量进行预测或控制. 在解决数据拟合问题时,首先应作出数据的散点图,然后通过观察散点的趋势选用相应的模型进行拟合. 为使散点图更清晰,可将数据适当简化或变换.
练 习
下表给出了八大行星与冥王星离太阳的距离和它们运行的周期,试建立这两组数据之间的关系.
解:在Excel表格中作出散点图,添加趋势线显示公式(模拟函数),
一次函数模型为 y=14.928x-4584.3,二次函数模型为 y=0.0015x2+6.410 9x-799.11.
阅 读
G大调的正弦函数
音乐,是人类精神通过无意识计算而获得的愉悦享受.
——G莱布尼茨
传说毕达哥拉斯很喜欢弹古希腊的七弦琴,他发现,当弦的粗细不变时,拨弄弦弹出的声音音高取决于各弦的长度,当弦的长度成简单的整数比时,它就发出和谐的声音.
从那时起,音乐的研究与数学连成了一体,数学家和音乐家都试图弄清音乐声音的本质,扩大音乐与数学两者之间的联系.
先考虑由音叉发出的简单的声音.
数学家研究发现,音叉发出的声音(音叉附近空气分子的振动)可以用函数模型 y=Asin ωt (A>0>0)来刻画,这是一个周期函数,最小正周期为.
有些声音悦耳动听,有些声音则叫人无法忍受. 同一个音符,为什么小提琴和钢琴发出的声音传到耳朵里会有不同的效果呢 观察发现,所有声音的图象都呈现周期性.
我们可以用小提琴和单簧管的声音图象加以证实,也可以用 father 一词中a 的声音的图象来证实,如图1所示.
如图 1所示的这种具有周期性的声音,在整体上来说是悦耳的称为音乐声音.
1807年,法国著名数学家傅里叶 (Fourier.1768-1830) 用一个幼粹的数学定理表述了这种规则特征:代表任何周期性声音的公式是形如 Asinωt 的简单正弦函数之和,而且这些正弦函数的频率都是其中一个最小频率的整数倍. 比如说图1中的小提琴的声音图象公式基本上是
y=0.06sin1000πt-0.02sin2 000πt-0.0lsin3 000πt.
首先,这个公式是简单的正弦表达式之和:其次,第 1项的频率是500,第2项的频率是1000,第3项的频率是1500. 因此,第2项和第3项的频率是最低频率的整数倍,这些简单三角函数的图象如图 2 所示.
例如,一个音质与上面的小提琴音质完全相同的声音,能够由 3个具有适当相关音量的、每个频率分别为 500,1 000,1500 的音叉同时发声而产生.因此,从理论上来讲,完全可以由音叉来演奏贝多芬第九交响曲.
通过傅里叶定理,我们明白了一般的音乐声音的数学特征:各种声音都可以归于一些简单声音的基本组合,而这些简单声音在数学上又不会比简单的三角函数更复杂.
上面简单的描述表明,数学已经深深地渗入到音乐领域中了
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
