人教版数学8年级下册 17.2 勾股定理的逆定理课时练(含答案)
文档属性
| 名称 | 人教版数学8年级下册 17.2 勾股定理的逆定理课时练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 127.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 10:47:13 | ||
图片预览



文档简介
17.2 勾股定理的逆定理
17.2.1 互逆命题与互逆定理
1.下列命题中,与“同旁内角互补,两直线平行”成为互逆定理的是( )
A.同旁内角不互补,两直线平行
B.同旁内角不互补,两直线不平行
C.两直线平行,同旁内角互补
D.两直线不平行,同旁内角不互补
2.命题“如果a>0,b>0,那么ab>0”的逆命题是 __________.
3.命题:若两个数相等,则它们的绝对值相等,它的逆命题是 __________.
4.“对顶角相等”这个命题的逆命题是__________.
5.命题“两直线平行,同位角相等”的逆命题是__________命题.(填“真”或“假”)
6.请写出一对是真命题的互逆命题:__________.
17.2.2 勾股定理的逆定理
1.下列各组数分别为一个三角形三边的长,其中能构成直角三角形的一组是( )
A.2,3,4 B.9,12,15 C.5,12,14 D.1,2,2
2.下列长度的三条线段能组成直角三角形的是( )
A.,, B.2,3,4
C.4,6,8 D.6,8,10
3.以下列各组数为边长,能构成直角三角形的是( )
A.1,2,3 B.1,, C.,, D.5,6,7
4.在△ABC中,若BC=24,AB=7,AC=25,则△ABC的形状是 __________.
5.如图,方格纸中每个小正方形的边长均为1,△ABC的顶点均为格点.判断△ABC的形状,并说明理由.
17.2.3 勾股数
1.下列各组数中,是勾股数的为( )
A.6,8,10 B.0.3,0.4,0.5 C.,1,1 D.2,3,4
2.下列选项中不是勾股数的是( )
A.7,24,25 B.4,5,6 C.3,4,5 D.9,12,15
3.有下列各组数:①3,4,5;②62,82,102;③0.5,1.2,1.3;④1,,.其中勾股数有( )
A.1组 B.2组 C.3组 D.4组
4.一组勾股数,若其中两个为15,8,则第三个数为 __________.
5.勾股数为一组连续自然数的是 __________.
6.古希腊的哲学家柏拉图曾指出,如果m表示大于1的整数,a=2m,b=m2﹣1,c=m2+1,那么a,b,c为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
17.2.4 勾股定理及其逆定理的综合运用
1.在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列条件中,能判定△ABC是直角三角形的是( )
A.a=2,b=3,c=4 B.a=2,b=5,c=5
C.a=5,b=8,c=10 D.a=7,b=24,c=25
2.已知△ABC的三边a=m2﹣1(m>1),b=2m,c=m2+1.
(1)求证:△ABC是直角三角形.
(2)利用第(1)题的结论,写出两个直角三角形的边长,要求它们的边长均为正整数.
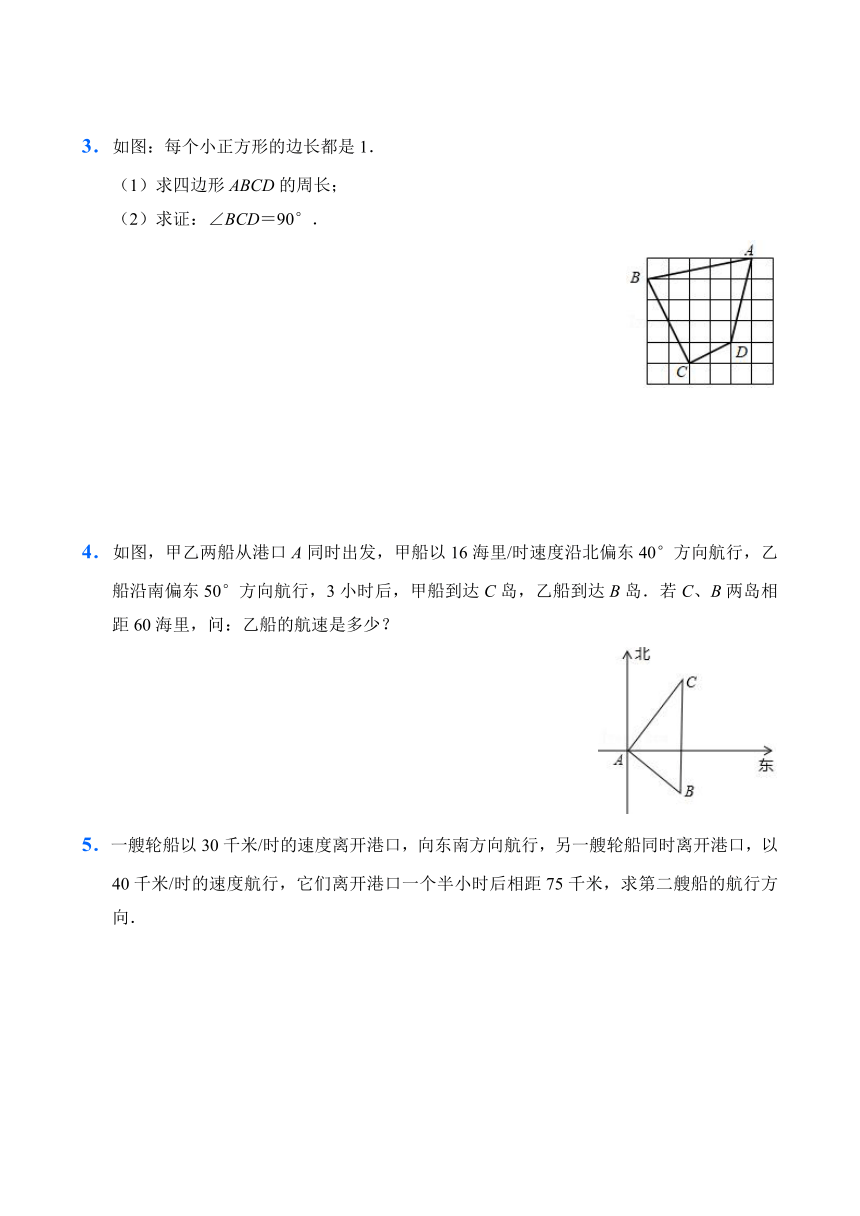
3.如图:每个小正方形的边长都是1.
(1)求四边形ABCD的周长;
(2)求证:∠BCD=90°.
4.如图,甲乙两船从港口A同时出发,甲船以16海里/时速度沿北偏东40°方向航行,乙船沿南偏东50°方向航行,3小时后,甲船到达C岛,乙船到达B岛.若C、B两岛相距60海里,问:乙船的航速是多少?
5.一艘轮船以30千米/时的速度离开港口,向东南方向航行,另一艘轮船同时离开港口,以40千米/时的速度航行,它们离开港口一个半小时后相距75千米,求第二艘船的航行方向.
参考答案及解析
17.2 勾股定理的逆定理
17.2.1 互逆命题与互逆定理
1.【答案】C
【解析】“同旁内角互补,两直线平行”的逆定理是两直线平行,同旁内角互补,故选C.
2.【答案】如果ab>0,那么a>0,b>0
【解析】略
3.【答案】绝对值相等的两个数相等
【解析】略
4.【答案】如果两个角相等,那么它们是对顶角
【解析】略
5.【答案】真
【解析】∵原命题的条件为:两直线平行,结论为:同位角相等.
∴其逆命题为:同位角相等,两直线平行.为真命题,故答案为:真.
6.【答案】直角三角形的两个锐角互余;有两个锐角互余的三角形是直角三角形(答案不唯一)
【解析】略
17.2.2 勾股定理的逆定理
1.【答案】B
【解析】A,22+32≠42,故A不符合题意;
B,92+122=152,故B符合题意;
C,52+122≠142,故C不符合题意;
D,12+22≠22,故D不符合题意.故选B.
2.【答案】D
【解析】A,()2+()2≠()2,故A不符合题意;
B,22+32≠42,故B不符合题意;
C,42+62≠82,故C不符合题意;
D,62+82=102,故D符合题意.故选D.
3.【答案】C
【解析】A,12+22≠32,故A不符合题意;
B,12+()2≠()2,故B不符合题意;
C,()2+()2=()2,故C符合题意;
D,52+62≠72,故D不符合题意.故选C.
4.【答案】直角三角形
【解析】∵△ABC中,BC=24,AB=7,AC=25,
∴72+242=252,即AC2=AB2+BC2,
∴△ABC是直角三角形.
故答案为:直角三角形.
5.【答案】△ABC是直角三角形,理由如下:
由题可得,AC2=22+42=20,BC2=22+12=5,AB2=32+42=25,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,且∠ACB=90°.
17.2.3 勾股数
1.【答案】A
【解析】A,∵62+82=102,∴是勾股数,符合题意;
B,∵0.3,0.4,0.5不是整数,∴不是勾股数,不符合题意;
C,∵不是整数,∴不是勾股数,不符合题意;
D,∵22+32≠42,∴不是勾股数,不符合题意.故选A.
2.【答案】B
【解析】A,,且7,24,25是正整数,,24,25是勾股数,A不符合题意;
B,,,5,6不是勾股数,B符合题意;
C,,且3,4,5是正整数,3,4,5是勾股数,C不符合题意;
D,,且9,12,15是正整数,9,12,15是勾股数,D不符合题意.故选B.
3.【答案】A
【解析】①32+42=52,是勾股数;
②(62)2+(82)2≠(102)2,不是勾股数;
③0.5,1.2,1.3不是整数,不是勾股数;
④1,,.不是整数,不是勾股数;
其中勾股数只有①,共1组,故选A.
4.【答案】17
【解析】设第三个数为x,∵15,8,x是一组勾股数,∴①x2+82=152,解得x=(不合题意,舍去),②152+82=x2,解得:x=17,故答案为:17.
5.【答案】3,4,5
【解析】设中间的数是x,那么前面的数就是x﹣1,后面的数是x+1,根据题意,得(x﹣1)2+x2=(x+1)2,解得x=0(舍去)或x=4;4﹣1=3,4+1=5.故答案为:3,4,5.
6.【答案】正确.理由如下:
∵m表示大于1的整数,
∴a,b,c都是正整数,且c是最大边,
∵(2m)2+(m2﹣1)2=(m2+1)2,
∴a2+b2=c2,即a,b,c为勾股数.
当m=3时,可得一组勾股数6,8,10.
17.2.4 勾股定理及其逆定理的综合运用
1.【答案】D
【解析】A,∵22+32=13≠42,∴A中的条件不能判定△ABC是直角三角形;
B,∵22+52=29≠52,∴B中的条件不能判定△ABC是直角三角形;
C,∵52+82=89≠102,∴C中的条件不能判定△ABC是直角三角形;
D,∵72+242=625=252,∴D中的条件可以判定△ABC是直角三角形.
故选D.
2.【答案】(1)∵△ABC的三边a=m2﹣1(m>1),b=2m,c=m2+1,
当m>1时,m2﹣1<m2+1,2m<m2+1,
∴(m2﹣1)2+(2m)2=m4+1﹣2m2+4m2=(m2+1)2,即a2+b2=c2,
∴△ABC是直角三角形;
(2)当m=2时,直角三角形的边长为3,4,5;
当m=3时,直角三角形的边长为8,6,10(答案不唯一).
3.【答案】(1)由题意可知AB,BC2,CD,AD,
∴四边形ABCD的周长为23;
(2)证明:连接BD.
∵BC=2,CD,BD5,
∴BC2+CD2=BD2,
∴△BCD是直角三角形,
∴∠BCD=90°.
4.【答案】∵甲船沿北偏东40°方向航行,乙船沿南偏东50°方向航行,
∴∠CAB=90°,
∵AB=16×3=48,BC=60,∴AC36,
∴乙船的航速是36÷3=12(海里/时)
答:乙船的航速是36÷3=12海里/时.
5.【答案】如图,根据题意,得
OA=30×1.5=45(千米),OB=40×1.5=60(千米),AB=75千米.
∵452+602=752,∴OA2+OB2=AB2,
∴∠AOB=90°,即第二艘船的航行方向与第一艘船的航行方向成90°,
∴第二艘船的航行方向为东北或西南方向.
17.2.1 互逆命题与互逆定理
1.下列命题中,与“同旁内角互补,两直线平行”成为互逆定理的是( )
A.同旁内角不互补,两直线平行
B.同旁内角不互补,两直线不平行
C.两直线平行,同旁内角互补
D.两直线不平行,同旁内角不互补
2.命题“如果a>0,b>0,那么ab>0”的逆命题是 __________.
3.命题:若两个数相等,则它们的绝对值相等,它的逆命题是 __________.
4.“对顶角相等”这个命题的逆命题是__________.
5.命题“两直线平行,同位角相等”的逆命题是__________命题.(填“真”或“假”)
6.请写出一对是真命题的互逆命题:__________.
17.2.2 勾股定理的逆定理
1.下列各组数分别为一个三角形三边的长,其中能构成直角三角形的一组是( )
A.2,3,4 B.9,12,15 C.5,12,14 D.1,2,2
2.下列长度的三条线段能组成直角三角形的是( )
A.,, B.2,3,4
C.4,6,8 D.6,8,10
3.以下列各组数为边长,能构成直角三角形的是( )
A.1,2,3 B.1,, C.,, D.5,6,7
4.在△ABC中,若BC=24,AB=7,AC=25,则△ABC的形状是 __________.
5.如图,方格纸中每个小正方形的边长均为1,△ABC的顶点均为格点.判断△ABC的形状,并说明理由.
17.2.3 勾股数
1.下列各组数中,是勾股数的为( )
A.6,8,10 B.0.3,0.4,0.5 C.,1,1 D.2,3,4
2.下列选项中不是勾股数的是( )
A.7,24,25 B.4,5,6 C.3,4,5 D.9,12,15
3.有下列各组数:①3,4,5;②62,82,102;③0.5,1.2,1.3;④1,,.其中勾股数有( )
A.1组 B.2组 C.3组 D.4组
4.一组勾股数,若其中两个为15,8,则第三个数为 __________.
5.勾股数为一组连续自然数的是 __________.
6.古希腊的哲学家柏拉图曾指出,如果m表示大于1的整数,a=2m,b=m2﹣1,c=m2+1,那么a,b,c为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
17.2.4 勾股定理及其逆定理的综合运用
1.在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列条件中,能判定△ABC是直角三角形的是( )
A.a=2,b=3,c=4 B.a=2,b=5,c=5
C.a=5,b=8,c=10 D.a=7,b=24,c=25
2.已知△ABC的三边a=m2﹣1(m>1),b=2m,c=m2+1.
(1)求证:△ABC是直角三角形.
(2)利用第(1)题的结论,写出两个直角三角形的边长,要求它们的边长均为正整数.
3.如图:每个小正方形的边长都是1.
(1)求四边形ABCD的周长;
(2)求证:∠BCD=90°.
4.如图,甲乙两船从港口A同时出发,甲船以16海里/时速度沿北偏东40°方向航行,乙船沿南偏东50°方向航行,3小时后,甲船到达C岛,乙船到达B岛.若C、B两岛相距60海里,问:乙船的航速是多少?
5.一艘轮船以30千米/时的速度离开港口,向东南方向航行,另一艘轮船同时离开港口,以40千米/时的速度航行,它们离开港口一个半小时后相距75千米,求第二艘船的航行方向.
参考答案及解析
17.2 勾股定理的逆定理
17.2.1 互逆命题与互逆定理
1.【答案】C
【解析】“同旁内角互补,两直线平行”的逆定理是两直线平行,同旁内角互补,故选C.
2.【答案】如果ab>0,那么a>0,b>0
【解析】略
3.【答案】绝对值相等的两个数相等
【解析】略
4.【答案】如果两个角相等,那么它们是对顶角
【解析】略
5.【答案】真
【解析】∵原命题的条件为:两直线平行,结论为:同位角相等.
∴其逆命题为:同位角相等,两直线平行.为真命题,故答案为:真.
6.【答案】直角三角形的两个锐角互余;有两个锐角互余的三角形是直角三角形(答案不唯一)
【解析】略
17.2.2 勾股定理的逆定理
1.【答案】B
【解析】A,22+32≠42,故A不符合题意;
B,92+122=152,故B符合题意;
C,52+122≠142,故C不符合题意;
D,12+22≠22,故D不符合题意.故选B.
2.【答案】D
【解析】A,()2+()2≠()2,故A不符合题意;
B,22+32≠42,故B不符合题意;
C,42+62≠82,故C不符合题意;
D,62+82=102,故D符合题意.故选D.
3.【答案】C
【解析】A,12+22≠32,故A不符合题意;
B,12+()2≠()2,故B不符合题意;
C,()2+()2=()2,故C符合题意;
D,52+62≠72,故D不符合题意.故选C.
4.【答案】直角三角形
【解析】∵△ABC中,BC=24,AB=7,AC=25,
∴72+242=252,即AC2=AB2+BC2,
∴△ABC是直角三角形.
故答案为:直角三角形.
5.【答案】△ABC是直角三角形,理由如下:
由题可得,AC2=22+42=20,BC2=22+12=5,AB2=32+42=25,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,且∠ACB=90°.
17.2.3 勾股数
1.【答案】A
【解析】A,∵62+82=102,∴是勾股数,符合题意;
B,∵0.3,0.4,0.5不是整数,∴不是勾股数,不符合题意;
C,∵不是整数,∴不是勾股数,不符合题意;
D,∵22+32≠42,∴不是勾股数,不符合题意.故选A.
2.【答案】B
【解析】A,,且7,24,25是正整数,,24,25是勾股数,A不符合题意;
B,,,5,6不是勾股数,B符合题意;
C,,且3,4,5是正整数,3,4,5是勾股数,C不符合题意;
D,,且9,12,15是正整数,9,12,15是勾股数,D不符合题意.故选B.
3.【答案】A
【解析】①32+42=52,是勾股数;
②(62)2+(82)2≠(102)2,不是勾股数;
③0.5,1.2,1.3不是整数,不是勾股数;
④1,,.不是整数,不是勾股数;
其中勾股数只有①,共1组,故选A.
4.【答案】17
【解析】设第三个数为x,∵15,8,x是一组勾股数,∴①x2+82=152,解得x=(不合题意,舍去),②152+82=x2,解得:x=17,故答案为:17.
5.【答案】3,4,5
【解析】设中间的数是x,那么前面的数就是x﹣1,后面的数是x+1,根据题意,得(x﹣1)2+x2=(x+1)2,解得x=0(舍去)或x=4;4﹣1=3,4+1=5.故答案为:3,4,5.
6.【答案】正确.理由如下:
∵m表示大于1的整数,
∴a,b,c都是正整数,且c是最大边,
∵(2m)2+(m2﹣1)2=(m2+1)2,
∴a2+b2=c2,即a,b,c为勾股数.
当m=3时,可得一组勾股数6,8,10.
17.2.4 勾股定理及其逆定理的综合运用
1.【答案】D
【解析】A,∵22+32=13≠42,∴A中的条件不能判定△ABC是直角三角形;
B,∵22+52=29≠52,∴B中的条件不能判定△ABC是直角三角形;
C,∵52+82=89≠102,∴C中的条件不能判定△ABC是直角三角形;
D,∵72+242=625=252,∴D中的条件可以判定△ABC是直角三角形.
故选D.
2.【答案】(1)∵△ABC的三边a=m2﹣1(m>1),b=2m,c=m2+1,
当m>1时,m2﹣1<m2+1,2m<m2+1,
∴(m2﹣1)2+(2m)2=m4+1﹣2m2+4m2=(m2+1)2,即a2+b2=c2,
∴△ABC是直角三角形;
(2)当m=2时,直角三角形的边长为3,4,5;
当m=3时,直角三角形的边长为8,6,10(答案不唯一).
3.【答案】(1)由题意可知AB,BC2,CD,AD,
∴四边形ABCD的周长为23;
(2)证明:连接BD.
∵BC=2,CD,BD5,
∴BC2+CD2=BD2,
∴△BCD是直角三角形,
∴∠BCD=90°.
4.【答案】∵甲船沿北偏东40°方向航行,乙船沿南偏东50°方向航行,
∴∠CAB=90°,
∵AB=16×3=48,BC=60,∴AC36,
∴乙船的航速是36÷3=12(海里/时)
答:乙船的航速是36÷3=12海里/时.
5.【答案】如图,根据题意,得
OA=30×1.5=45(千米),OB=40×1.5=60(千米),AB=75千米.
∵452+602=752,∴OA2+OB2=AB2,
∴∠AOB=90°,即第二艘船的航行方向与第一艘船的航行方向成90°,
∴第二艘船的航行方向为东北或西南方向.
