15.2 数据的表示 课件(共31张PPT)
文档属性
| 名称 | 15.2 数据的表示 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 08:25:04 | ||
图片预览










文档简介
(共31张PPT)
15.2 数据的表示
数学(华东师大版)
八年级 上册
第15章 数据的收集与表示
学习目标
1.理解扇形统计图的特点,会制作扇形统计图;
2.能够根据统计图中提供的信息作出合理的判断,并能用自己的语言清楚的表达出来;
3.学会对所收集到的数据进行统计表示;
4.学会用多种方法来表示数据;
温故知新
统计图:
扇形统计图
条形统计图
期中
30%
期末
60%
平时
10%
3
4
5
6
7
8
棵数
12
10
8
6
4
2
0
人
数
折线统计图
同学们我们生活在一个数据的时代,学会数据的收集和整理能够解决很多实际问题,回想一下在以前的学习中我们用过哪些统计图?
导入新课
条形统计图
折线统计图
扇形统计图
讲授新课
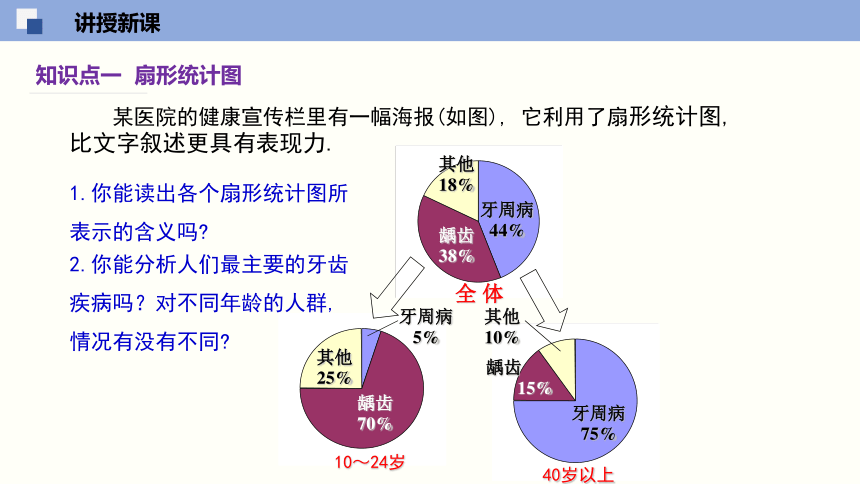
知识点一 扇形统计图
某医院的健康宣传栏里有一幅海报(如图), 它利用了扇形统计图, 比文字叙述更具有表现力.
其他
18%
牙周病
44%
龋齿
38%
其他
25%
龋齿
70%
牙周病
5%
牙周病
75%
龋齿
15%
其他
10%
全 体
10~24岁
40岁以上
1.你能读出各个扇形统计图所表示的含义吗
2.你能分析人们最主要的牙齿疾病吗?对不同年龄的人群, 情况有没有不同
讲授新课
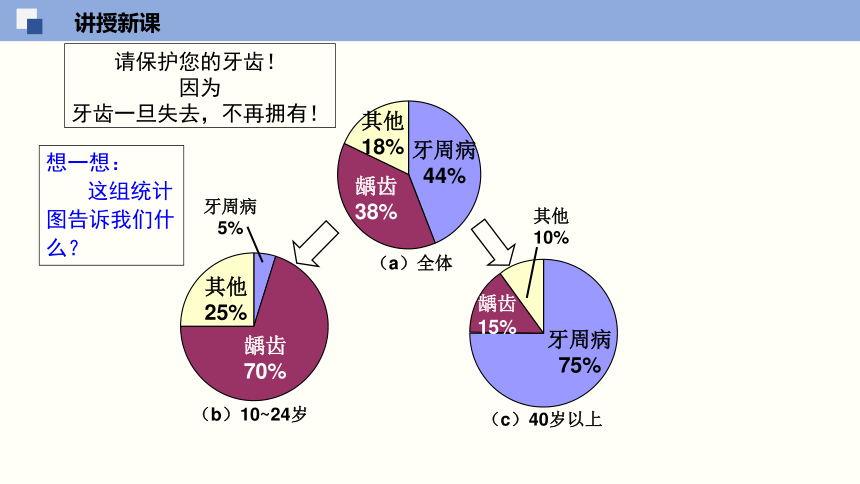
想一想:
这组统计图告诉我们什么?
请保护您的牙齿!
因为
牙齿一旦失去,不再拥有!
其他
18%
牙周病
44%
龋齿
38%
牙周病
75%
龋齿
15%
其他
10%
其他
25%
龋齿
70%
牙周病
5%
(a)全体
(b)10~24岁
(c)40岁以上
讲授新课
1.上图所示的每个圆中所有扇形表示的百分比之和为多少?
2.量一量,每个扇形的圆心角度数是多少
3.同一个扇形统计图中各扇形圆心角的大小与图上所标的相应百分比之间有什么关系?
4.如果不用量角器测量,你能根据百分比计算各个圆心角的度数吗?
根据统计图,回答下列问题:
因为扇形统计图可以清楚地告诉我们各部分数量占总数量的百分比,所以我们在表示各部分数量在总数量中所占份额时常常使用扇形统计图.
讲授新课
2.扇形代表
3.扇形的大小反映
1.圆代表
总体
总体中的不同部分
部分占总体的百分比的大小
用圆和扇形分别表示总体和各个组成部分数据的统计图叫做扇形统计图.
知识归纳
讲授新课
1.计算各部分数量占总数量的百分比: (部分÷总体)×100%
4.注明相应的百分比.各成分的名称可以注在图上,也可以用图例表明.
2.计算相应的扇形圆心角的度数:
3.画圆及扇形:
画适度大小的圆, 并按圆心角的度数度
量画出各部分扇形.
360° 百分比
绘制扇形统计图的一般步骤:
讲授新课
典例精析
【例1】根据下表,你能用扇形统计图把各大洲土地面积占全球土地总面积的百分比表示出来吗?有条件的话,请尝试用计算机中的Excel软件帮你作图.(精确到0.1%)
洲名 亚洲 非洲 欧洲 北美洲 南美洲 大洋洲 南极洲
土地面积 (万平方千米) 4400 3020 1016 2422.8 1797 897 1400
七大洲土地面积表
讲授新课
洲名 亚洲 非洲 欧洲 北美洲 南美洲 大洋洲 南极洲
土地面积 (万平方千米) 4400 3020 1016 2422.8 1797 897 1400
七大洲土地面积表
29.4%
20.2%
6.8%
16.2%
12.0%
6.0%
9.4%
讲授新课
知识点二 利用统计图表传递信息
(1)中国体育健儿在该届奥运会上共获得多少枚奖牌?获得的金牌数在总金牌数中占多大的比例?
(2)从所获奖牌的总数看,和最近几届奥运会相比,中国体育健儿在本届奥运会上的成绩如何?
讲授新课
(1)中国体育健儿在该届奥运会上共获得多少枚奖牌?获得的金牌数在总金牌数中占多大的比例?(总金牌数302枚)
代表团 金牌 银牌 铜牌 总计
美国 29届 36 38 36 110
30届 46 29 29 104
中国 29届 51 21 28 100
30届 38 27 23 88
俄罗斯 29届 23 21 29 73
30届 24 26 32 82
英国 29届 19 13 15 47
30届 29 17 19 65
奥运奖牌榜(第29、30届)
约占该届奥运会总金牌数302枚的13% .
中国体育健儿在第30届奥运会上共获得88枚奖牌,其中金牌38枚;
讲授新课
代表团 金牌 银牌 铜牌 总计
美国 29届 36 38 36 110
30届 46 29 29 104
中国 29届 51 21 28 100
30届 38 27 23 88
俄罗斯 29届 23 21 29 73
30届 24 26 32 82
英国 29届 19 13 15 47
30届 29 17 19 65
奥运奖牌榜(第29、30届)
(1)中国体育健儿在该届奥运会上共获得多少枚奖牌?获得的金牌数在总金牌数中占多大的比例?
讲授新课
(1)中国体育健儿在该届奥运会上共获得多少枚奖牌?获得的金牌数在总金牌数中占多大的比例?
15%
13%
54%
讲授新课
(2)从所获奖牌的总数看,和最近几届奥运会相比,中国体育健儿在本届奥运会上的成绩如何?
届数 金牌 银牌 铜牌 总计
24 5 11 12 28
25 16 22 16 54
26 16 22 12 50
27 28 16 15 59
28 32 17 14 63
29 51 21 28 100
30 38 27 23 88
中国奥运奖牌数回眸
讲授新课
思 考
(1)在图中用一条折线将七届奥运会的数据连起来了,请问介于相邻两届之间的六条线段是否表示某种意思?连线是为了显示什么?
中国代表团奖牌数量随着时间的变化规律
(2)与第29届北京奥运会相比,我国代表团在这一届获得的奖牌总数有所下降,你怎么解释这个结果呢?
讲授新课
思 考
下面两图传达的信息对你的分析有帮助吗
讲授新课
概括
条形统计图是用宽度相同的条形的高低或长短来表示数据特征的统计图,它可以直观地反映出数据的数量特征.
如果有两个研究对象,常常把这两个对象的相应数据并列表示在同一幅条形统计图中.
讲授新课
概括
扇形统计图是用整个圆代表所研究的总体,用圆中各个扇形代表组成总体的各个部分,扇形圆心角的大小反映出各组成部分的数量在总数量中所占份额的大小.
讲授新课
概括
折线统计图是用折线表示数量变化规律的统计图. 如果关注的是某种现象随时间变化而发生的变化,常常以时间为水平放置的数轴,以折线的起伏直观地反映出数量随时间所发生的相应变化.
当堂检测
1、下列说法错误的是( )
A.频率分布反映了一组数据落在各个小组范围内的比例大小
B.频数是一组数据中,落在各个小组内的数据
C.频数分布表中,各小组频数之和等于样本的总数
D.频率分布表中,各小组的频率之和为1
【详解】解:A、频率分布反映了一组数据落在各个小组范围内的比例大小,原说法正确,不符合题意;
B、频数是一组数据中,落在各个小组内的数据的个数,原说法错误,符合题意;
C、频数分布表中,各小组频数之和等于样本的总数,原说法正确,不符合题意;
D、频率分布表中,各小组的频率之和为,原说法正确,不符合题意.
故选B.
当堂检测
2、“世界杯”期间,小军调查了全班同学对A、B、C、D四位足球明星的喜欢程度,将结果制成统计图(如图),最受学生喜欢的明星的频率是________.
【详解】解:,
∴最受学生喜欢的明星的频率是0.5,
故答案为:0.5.
【点睛】本题主要考查了求频率,频数分布直方图,熟知频率=频数÷总数是解题的关键.
当堂检测
3.在列频率分布表时,得到一组数据中某一个数据的频数是12,频率是0.2,那么这个数据组中共有________个数据.
【详解】解:12÷0.2=60(个),
∴这个数据组中共有60个数据,
故答案为:60.
当堂检测
4.为了了解学生在家做家务情况,某校对部分学生进行抽样调查,并绘制了如图所示的频数分布直方图(每组数据含最小值,不含最大值).如果该校有1500名学生,估计该校平均每周做家务的时间少于2小时的学生人数约是______人.
【详解】解:如果该校有1500名学生,估计该校平均每周做家务的时间少于2小时的学生人数约是1500×,
故答案为:720.
当堂检测
5.2022年10月12日,“天宫课堂”第三课开讲,为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),A组:75≤x≤80,B组:80≤x≤85,C组:85≤x≤90,D组:90≤x≤95,E组:95≤x≤100,并绘制了如下不完整的统计图.请结合统计图,解答下列问题:
(1)频数分布直方图中m=__________;
(2)补全学生成绩频数分布直方图;
(3)若成绩在90分及以上为优秀,学校共有4500名学生,估计该校成绩优秀的学生有多少人?
当堂检测
【详解】(1)解:本次调查一共随机抽取的学生总人数为:96÷24%=400(名),
∴B组的人数为:400×15%=60(名),
∴m=60.
故答案为:60.
(2)解:E组的人数为:400-20-60-96-144=80(人).
补全学生成绩额数分布直方图如下:
(3)解:4500×(人).
∴估计该校成绩优秀的学生有2520人.
当堂检测
6.某中学八年级共有400名学生,学校为了增强学生的国防意识,在本年级进行了一次国防知识测验.为了了解这次测验的成绩状况,从中抽取了50名学生的成绩,将所得数据整理后,画出频数分布直方图如图所示.
(1)图中第五个小组的频数是多少?
(2)第四小组和第五个小组的频率各是多少?
(3)这次测验中,八年级全体学生成绩在59.5—69.5中的人数约是多少?
当堂检测
【详解】(1)解:由图可知,第四个小组的频数是13,
∴第五个小组的频数:50-5-9-13×2=10.
(2)解:第四小组的频率:,
第五小组的频率:;
(3)解:400×(人),
答:八年级全体学生成绩在59.5—69.5中的人数约是72人.
课堂小结
扇形统计图
注意:(1)各个扇形所占的百分比之和为1;
(2)各个扇形的圆心角度数之和为360°;
(3)画扇形时勿将圆心角与百分比相混淆.
绘制扇形统计图的步骤
谢 谢~
15.2 数据的表示
数学(华东师大版)
八年级 上册
第15章 数据的收集与表示
学习目标
1.理解扇形统计图的特点,会制作扇形统计图;
2.能够根据统计图中提供的信息作出合理的判断,并能用自己的语言清楚的表达出来;
3.学会对所收集到的数据进行统计表示;
4.学会用多种方法来表示数据;
温故知新
统计图:
扇形统计图
条形统计图
期中
30%
期末
60%
平时
10%
3
4
5
6
7
8
棵数
12
10
8
6
4
2
0
人
数
折线统计图
同学们我们生活在一个数据的时代,学会数据的收集和整理能够解决很多实际问题,回想一下在以前的学习中我们用过哪些统计图?
导入新课
条形统计图
折线统计图
扇形统计图
讲授新课
知识点一 扇形统计图
某医院的健康宣传栏里有一幅海报(如图), 它利用了扇形统计图, 比文字叙述更具有表现力.
其他
18%
牙周病
44%
龋齿
38%
其他
25%
龋齿
70%
牙周病
5%
牙周病
75%
龋齿
15%
其他
10%
全 体
10~24岁
40岁以上
1.你能读出各个扇形统计图所表示的含义吗
2.你能分析人们最主要的牙齿疾病吗?对不同年龄的人群, 情况有没有不同
讲授新课
想一想:
这组统计图告诉我们什么?
请保护您的牙齿!
因为
牙齿一旦失去,不再拥有!
其他
18%
牙周病
44%
龋齿
38%
牙周病
75%
龋齿
15%
其他
10%
其他
25%
龋齿
70%
牙周病
5%
(a)全体
(b)10~24岁
(c)40岁以上
讲授新课
1.上图所示的每个圆中所有扇形表示的百分比之和为多少?
2.量一量,每个扇形的圆心角度数是多少
3.同一个扇形统计图中各扇形圆心角的大小与图上所标的相应百分比之间有什么关系?
4.如果不用量角器测量,你能根据百分比计算各个圆心角的度数吗?
根据统计图,回答下列问题:
因为扇形统计图可以清楚地告诉我们各部分数量占总数量的百分比,所以我们在表示各部分数量在总数量中所占份额时常常使用扇形统计图.
讲授新课
2.扇形代表
3.扇形的大小反映
1.圆代表
总体
总体中的不同部分
部分占总体的百分比的大小
用圆和扇形分别表示总体和各个组成部分数据的统计图叫做扇形统计图.
知识归纳
讲授新课
1.计算各部分数量占总数量的百分比: (部分÷总体)×100%
4.注明相应的百分比.各成分的名称可以注在图上,也可以用图例表明.
2.计算相应的扇形圆心角的度数:
3.画圆及扇形:
画适度大小的圆, 并按圆心角的度数度
量画出各部分扇形.
360° 百分比
绘制扇形统计图的一般步骤:
讲授新课
典例精析
【例1】根据下表,你能用扇形统计图把各大洲土地面积占全球土地总面积的百分比表示出来吗?有条件的话,请尝试用计算机中的Excel软件帮你作图.(精确到0.1%)
洲名 亚洲 非洲 欧洲 北美洲 南美洲 大洋洲 南极洲
土地面积 (万平方千米) 4400 3020 1016 2422.8 1797 897 1400
七大洲土地面积表
讲授新课
洲名 亚洲 非洲 欧洲 北美洲 南美洲 大洋洲 南极洲
土地面积 (万平方千米) 4400 3020 1016 2422.8 1797 897 1400
七大洲土地面积表
29.4%
20.2%
6.8%
16.2%
12.0%
6.0%
9.4%
讲授新课
知识点二 利用统计图表传递信息
(1)中国体育健儿在该届奥运会上共获得多少枚奖牌?获得的金牌数在总金牌数中占多大的比例?
(2)从所获奖牌的总数看,和最近几届奥运会相比,中国体育健儿在本届奥运会上的成绩如何?
讲授新课
(1)中国体育健儿在该届奥运会上共获得多少枚奖牌?获得的金牌数在总金牌数中占多大的比例?(总金牌数302枚)
代表团 金牌 银牌 铜牌 总计
美国 29届 36 38 36 110
30届 46 29 29 104
中国 29届 51 21 28 100
30届 38 27 23 88
俄罗斯 29届 23 21 29 73
30届 24 26 32 82
英国 29届 19 13 15 47
30届 29 17 19 65
奥运奖牌榜(第29、30届)
约占该届奥运会总金牌数302枚的13% .
中国体育健儿在第30届奥运会上共获得88枚奖牌,其中金牌38枚;
讲授新课
代表团 金牌 银牌 铜牌 总计
美国 29届 36 38 36 110
30届 46 29 29 104
中国 29届 51 21 28 100
30届 38 27 23 88
俄罗斯 29届 23 21 29 73
30届 24 26 32 82
英国 29届 19 13 15 47
30届 29 17 19 65
奥运奖牌榜(第29、30届)
(1)中国体育健儿在该届奥运会上共获得多少枚奖牌?获得的金牌数在总金牌数中占多大的比例?
讲授新课
(1)中国体育健儿在该届奥运会上共获得多少枚奖牌?获得的金牌数在总金牌数中占多大的比例?
15%
13%
54%
讲授新课
(2)从所获奖牌的总数看,和最近几届奥运会相比,中国体育健儿在本届奥运会上的成绩如何?
届数 金牌 银牌 铜牌 总计
24 5 11 12 28
25 16 22 16 54
26 16 22 12 50
27 28 16 15 59
28 32 17 14 63
29 51 21 28 100
30 38 27 23 88
中国奥运奖牌数回眸
讲授新课
思 考
(1)在图中用一条折线将七届奥运会的数据连起来了,请问介于相邻两届之间的六条线段是否表示某种意思?连线是为了显示什么?
中国代表团奖牌数量随着时间的变化规律
(2)与第29届北京奥运会相比,我国代表团在这一届获得的奖牌总数有所下降,你怎么解释这个结果呢?
讲授新课
思 考
下面两图传达的信息对你的分析有帮助吗
讲授新课
概括
条形统计图是用宽度相同的条形的高低或长短来表示数据特征的统计图,它可以直观地反映出数据的数量特征.
如果有两个研究对象,常常把这两个对象的相应数据并列表示在同一幅条形统计图中.
讲授新课
概括
扇形统计图是用整个圆代表所研究的总体,用圆中各个扇形代表组成总体的各个部分,扇形圆心角的大小反映出各组成部分的数量在总数量中所占份额的大小.
讲授新课
概括
折线统计图是用折线表示数量变化规律的统计图. 如果关注的是某种现象随时间变化而发生的变化,常常以时间为水平放置的数轴,以折线的起伏直观地反映出数量随时间所发生的相应变化.
当堂检测
1、下列说法错误的是( )
A.频率分布反映了一组数据落在各个小组范围内的比例大小
B.频数是一组数据中,落在各个小组内的数据
C.频数分布表中,各小组频数之和等于样本的总数
D.频率分布表中,各小组的频率之和为1
【详解】解:A、频率分布反映了一组数据落在各个小组范围内的比例大小,原说法正确,不符合题意;
B、频数是一组数据中,落在各个小组内的数据的个数,原说法错误,符合题意;
C、频数分布表中,各小组频数之和等于样本的总数,原说法正确,不符合题意;
D、频率分布表中,各小组的频率之和为,原说法正确,不符合题意.
故选B.
当堂检测
2、“世界杯”期间,小军调查了全班同学对A、B、C、D四位足球明星的喜欢程度,将结果制成统计图(如图),最受学生喜欢的明星的频率是________.
【详解】解:,
∴最受学生喜欢的明星的频率是0.5,
故答案为:0.5.
【点睛】本题主要考查了求频率,频数分布直方图,熟知频率=频数÷总数是解题的关键.
当堂检测
3.在列频率分布表时,得到一组数据中某一个数据的频数是12,频率是0.2,那么这个数据组中共有________个数据.
【详解】解:12÷0.2=60(个),
∴这个数据组中共有60个数据,
故答案为:60.
当堂检测
4.为了了解学生在家做家务情况,某校对部分学生进行抽样调查,并绘制了如图所示的频数分布直方图(每组数据含最小值,不含最大值).如果该校有1500名学生,估计该校平均每周做家务的时间少于2小时的学生人数约是______人.
【详解】解:如果该校有1500名学生,估计该校平均每周做家务的时间少于2小时的学生人数约是1500×,
故答案为:720.
当堂检测
5.2022年10月12日,“天宫课堂”第三课开讲,为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),A组:75≤x≤80,B组:80≤x≤85,C组:85≤x≤90,D组:90≤x≤95,E组:95≤x≤100,并绘制了如下不完整的统计图.请结合统计图,解答下列问题:
(1)频数分布直方图中m=__________;
(2)补全学生成绩频数分布直方图;
(3)若成绩在90分及以上为优秀,学校共有4500名学生,估计该校成绩优秀的学生有多少人?
当堂检测
【详解】(1)解:本次调查一共随机抽取的学生总人数为:96÷24%=400(名),
∴B组的人数为:400×15%=60(名),
∴m=60.
故答案为:60.
(2)解:E组的人数为:400-20-60-96-144=80(人).
补全学生成绩额数分布直方图如下:
(3)解:4500×(人).
∴估计该校成绩优秀的学生有2520人.
当堂检测
6.某中学八年级共有400名学生,学校为了增强学生的国防意识,在本年级进行了一次国防知识测验.为了了解这次测验的成绩状况,从中抽取了50名学生的成绩,将所得数据整理后,画出频数分布直方图如图所示.
(1)图中第五个小组的频数是多少?
(2)第四小组和第五个小组的频率各是多少?
(3)这次测验中,八年级全体学生成绩在59.5—69.5中的人数约是多少?
当堂检测
【详解】(1)解:由图可知,第四个小组的频数是13,
∴第五个小组的频数:50-5-9-13×2=10.
(2)解:第四小组的频率:,
第五小组的频率:;
(3)解:400×(人),
答:八年级全体学生成绩在59.5—69.5中的人数约是72人.
课堂小结
扇形统计图
注意:(1)各个扇形所占的百分比之和为1;
(2)各个扇形的圆心角度数之和为360°;
(3)画扇形时勿将圆心角与百分比相混淆.
绘制扇形统计图的步骤
谢 谢~
