13.2 三角形全等的判定(第5课时) 课件(共28张PPT)
文档属性
| 名称 | 13.2 三角形全等的判定(第5课时) 课件(共28张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 00:00:00 | ||
图片预览





文档简介
13.2 三角形全等的判定
第5课时 HL证全等
数学(华东师大版)
八年级 上册
第13章 全等三角形
学习目标
1、已知斜边、直角边会画直角三角形,经历画直角三角形探究得到“H.L.”定理,体会“H.L.”的合理性;
2、掌握“H.L.”定理,能正确应用“H.L.”定理证明两个三角形全等;
3、能正确应用所学的全等三角形的判定定理解决问题;
温故知新
问题:证明一般三角形全等有哪些方法?
1. 两边及其夹角分别相等的两个三角形全等.
简记为 S.A.S.(或边角边)
2.两角及其夹边分别相等的两个三角形全等.
简记为 A.S.A.(或角边角)
温故知新
3.两角分别相等且其中一组等角的对边相等的两个三角形全等.
简记为 A.A.S.(或角角边).
4.三边分别相等的两个三角形全等.
简记为 S.S.S.(或边边边)
导入新课
A
B
O
N
M
P
∟
∟
?
?
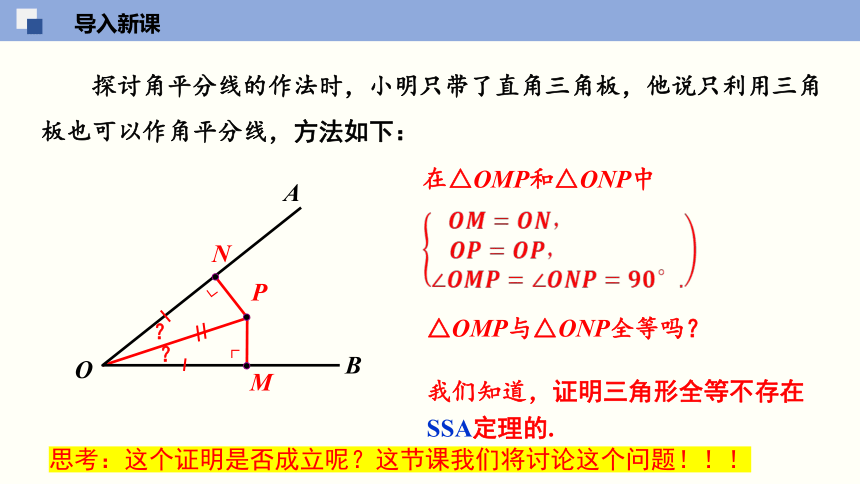
在△OMP和△ONP中
△OMP与△ONP全等吗?
????????=????????,??????????????????????????=????????,???????????????????∠????????????=∠????????????=????????°.
?
探讨角平分线的作法时,小明只带了直角三角板,他说只利用三角板也可以作角平分线,方法如下:
我们知道,证明三角形全等不存在SSA定理的.
思考:这个证明是否成立呢?这节课我们将讨论这个问题!!!
讲授新课
知识点一 利用“H.L.”判定直角三角形全等
舞台背景的形状是两个直角三角形,工作人员想知道两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住,无法测量.
(1) 你能帮他想个办法吗?
根据“S.A.S.”可测量其余两边与这两边的夹角.
根据“A.S.A.”,“A.A.S.”可测量对应一边和一锐角.
讲授新课
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等.于是,他就肯定“两个直角三角形是全等的”.
你相信这个结论吗?
(2)如果他只带一个卷尺,能完成这个任务吗?
下面,让我们来验证这个结论.
斜边和一条直角边对应相等→两个直角三角形全等?.
讲授新课
2 cm
3 cm
步骤:
1.画一条线段AB,使它等于2cm;
2.画∠MAB=90°(用量角器或三角尺);
3.以点B为圆心、3cm长为半径画圆弧,交射线AM于C;
△ABC即为所求.
M
A
B
C
把你画的直角三角形与其他同学画的直角三角形相比较,它们全等吗?
做一做
如图,已知两条线段,试画一个直角三角形,使长的线段为其斜边、短的线段为其一条直角边.
4.连结BC.
讲授新课
知识要点
“斜边直角边”判定方法
文字语言:
斜边和一条直角边分别相等的两个直角三角形全等
(简写成“斜边直角边”或“H.L.”).
几何语言:
A
B
C
A ′
B′
C ′
∴在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (H.L.).
∵∠C=∠C′=90°,
“S.S.A.”可以判定两个直角三角形全等,但是“边边”指的是斜边和一直角边,而“角”指的是直角.
AB=A′B′,
BC=B′C′,
讲授新课
典例精析
【例1】如图,已知 AC = BD,∠C = ∠D = 90°.求证: BC = AD.
证明: ∵∠C = ∠D = 90°(已知),
∴△ABC与△BAD 都是直角三角形(直角三角形的定义).
在Rt△ABC 与 Rt△BAD 中,
∵AB = BA (公共边),
AC = BD (已知),
∴Rt△ABC ≌ Rt△BAD (H.L.)
BC = AD (全等三角形的对应边相等).
讲授新课
1. 一般三角形的全等与直角三角形的全等是从一般到特殊的关系,二者之间的联系为: 一般三角形的判定方法同样适用于直角三角形.
2.判定一般三角形的全等与直角三角形的全等的区别:
(1)一般三角形全等的条件“S.S.S.”在直角三角形中被“H.L.”代替,无需找第三条边对应相等;
(2)“两边及其中一边的对角对应相等”不能判定一般三角形全等,但能判定直角三角形全等.
讲授新课
练一练
如图,在△ABC中,D为 BC 的中点,DE⊥AB,DF⊥AC,点 E、F 为垂足,DE = DF. 求证:△BED≌△CFD.
证明: ∵ DE ⊥ AB,DF ⊥ AC,
∴ ∠BED = ∠CFD = 90°,
∴△BED 与△CFD 都是直角三角形.
∵D 为 BC 的中点,
∴BD = CD .
在 Rt△BED 与 Rt△CFD 中,
∵BD = CD ,DE = DF,
∴Rt△BED ≌ Rt△CFD (H.L.).
讲授新课
2. 如图,AC = AD,∠C =∠D = 90°.求证: BC = BD.
证明:在Rt△ACB 和Rt△ADB 中,
∵AB=AB,AC=AD ,
∴Rt△ACB≌ Rt△ADB (H.L.).
∴BC = BD .
讲授新课
如图,有两个长度相同的滑梯,左边滑梯的高度 AC 与右边滑梯水平方向的跨度 DF 相等,两个滑梯的倾斜角∠B 与 ∠F 的大小有什么关系?说说你的想法和理由.
解: ∠B+∠F = 90°.
可以利用已知条件证明
Rt△ABC ≌ Rt△DEF (H.L.),
∴∠B =∠DEF,
∴∠B+∠F = 90°.
讲授新课
4. 如图,在△ABC中,AB = AC,AD是边 BC 上的高.
求证:(1)BD = DC;(2)∠BAD = ∠CAD.
证明: ∵AD 是 BC 边上的高,
∴∠ADB =∠ADC=90°.
在Rt△ADB 和Rt△ADC 中,
AB=AC,AD = AD,
∴Rt△ADB ≌ Rt△ADC (H.L.),
∴BD = DC,∠BAD =∠CAD .
讲授新课
5、一名工作人员不慎将一块三角形模具打碎成两块,他是否可以只带其中一块碎片到商店去,就能配一块与原来一样的三角形模具呢?他该带哪块去呢?请用数学知识解释你的结论.
解:可以.带右边的一块去.这样可以根据三角形全等的判定方法可知,具有全等的 3 个条件,即 A.S.A.
当堂检测
1、已知:如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°,
求证:②AO﹦BO,CO=DO.
A
D
C
B
②证明:在△AOC 和△BOD 中,
O
∠????=∠????已知,??????????????????∠????????????=∠????????????(对顶角相等),????????????=????????已证.??????????????????????
?
∴△AOC≌△BOD(AAS)
∴AO﹦BO,CO=DO(全等三角形对应边相等).
当堂检测
A
D
C
B
2.如图,AB⊥BD,CD⊥DB,AD=BC.求证:AB=CD,AD//BC.
证明:∵ AB⊥BD,CD⊥DB(已知),
∴∠ABD=∠CDB=90° (垂直定义).
在Rt△ABD和Rt△CDB中
????????=??????????(公共边)?,????????=????????(已知)?,???????
∴Rt△ABD≌Rt△CDB(HL).
∴∠ADB=∠CBD, AB=CD
(全等三角形对应边、对应角相等) .
∴ AD//BC(内错角相等,两直线平行) .
?
当堂检测
3.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,
AC=AE. 求证:BC=BE.
E
D
A
C
B
F
证明:∵ AD,AF分别是△ABC和△ABE的高,
∴∠ADB=∠AFB=90°
在Rt△ADC和Rt△AFE中, ????????=????????,????????=????????,?
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
在Rt△ADB和Rt△AFB中, ????????=????????,????????=????????,?
∴Rt△ADB≌Rt△AFB(HL).
∴BD=BF.
∴BD-CD=BF-EF.即BC=BE.
?
当堂检测
4. 如图所示,BE⊥AC,CF⊥AB,垂足分别是E、F.若BE=CF,则图中全等三角形有( )
A. 1对 B. 2对 C. 3对 D. 4对
C
A
F
C
B
E
根据全等的条件将全等的三角形一一列出即可;
当堂检测
5. 如图,已知AC⊥BD于点P,AP=CP,请增加一个条件,使△ABP≌△CDP(不能添加辅助线).
A
B
C
D
P
(1)若以“SAS”为依据,则可添加条件___________;
(2)若以“HL”为依据,则可添加条件___________ ;
(3)若以“ASA”为依据,则可添加条件__________ ;
(4)若以“AAS”为依据,则可添加条件___________.
BP=DP
AB=CD
∠A=∠C
∠B=∠D
当堂检测
6.如图,在四边形ABCD中,AB=AD,CA平分∠BCD,AE⊥BC于点E,AF⊥CD交CD的延长线于点F.
求证:△ABE≌△ADF.
A
D
C
B
F
E
证明:∵CA平分∠BCD,
∴∠ACE=∠ACF.
∵AE⊥BC于点E,AF⊥CD交CD的延长线于点F,
∴∠AEC=∠AFC=90°.
又∵AC=AC,
∴△ACE≌△ACF(AAS),
∴AE=AF.
在Rt△ABE和Rt△ADF中,
????????=????????,????????=????????,?
∴Rt△ABE≌Rt△ADF(HL).
?
当堂检测
7.如图,已知AD,BC相交于点O,AB=CD,AM⊥BC于点M,DN⊥BC于点N,BN=CM.
(1)求证:△ABM≌△DCN.
O
C
A
D
B
M
N
(1)证明:∵BN=CM
∴BN+MN=CM+MN,即:BM=CN,
∵AM⊥BC,DN⊥BC,
∴∠AMN=∠DNC=90°,
在Rt△ABM和Rt △ DCN中:
????????=????????,????????=????????,?
∴△ABM≌△DCN(HL);
?
当堂检测
O
C
A
D
B
M
N
(2)解:OA=OD,理由如下:
∵△ABM≌△DCN,
∴AM=DN,
在△AMO和△DNO中:
∠????????????=∠????????????=????????°,∠????????????=∠????????????,????????????=????????.??????????????????????
∴△AMO≌△DNO(AAS),
∴OA=OD.
?
(2)试猜想OA与OD的大小关系,并说明理由.
当堂检测
2.有一Rt△ABC,∠C=90°,AC=10cm,BC=5cm,线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AM上运动,问P点运动到AC上什么位置时,△ABC才能和△APQ全等?
B
C
A
P
Q
M
5cm
5cm
解:(1)当P运动到AP=BC时,
∵∠C=∠QAP=90°.
在Rt△ABC与Rt△QPA中,
????????=????????,????????=????????,??
∴Rt△ABC≌Rt△QPA(HL),
∴AP=BC=5cm;
?
第二种情况:
当堂检测
B
C
A
(P)
Q
M
10cm
5cm
(2)当P运动到与C点重合时,AP=AC.
在Rt△ABC与Rt△QPA中,
????????=????????,????????=????????,?
∴Rt△QAP≌Rt△BCA(HL),
∴AP=AC=10cm,
∴当AP=5cm或10cm时,
△ABC才能和△APQ全等.
?
第二种情况:
课堂小结
斜边直角边
判定定理
形式
斜边和一条直角边分别相等的两个直角三角形全等
H.L.(斜边直角边),存在于直角三角形中
判定直角三角形全等与判定一般三角形全等的联系与区别
应用
用H.L.解决问题
谢 谢~
第5课时 HL证全等
数学(华东师大版)
八年级 上册
第13章 全等三角形
学习目标
1、已知斜边、直角边会画直角三角形,经历画直角三角形探究得到“H.L.”定理,体会“H.L.”的合理性;
2、掌握“H.L.”定理,能正确应用“H.L.”定理证明两个三角形全等;
3、能正确应用所学的全等三角形的判定定理解决问题;
温故知新
问题:证明一般三角形全等有哪些方法?
1. 两边及其夹角分别相等的两个三角形全等.
简记为 S.A.S.(或边角边)
2.两角及其夹边分别相等的两个三角形全等.
简记为 A.S.A.(或角边角)
温故知新
3.两角分别相等且其中一组等角的对边相等的两个三角形全等.
简记为 A.A.S.(或角角边).
4.三边分别相等的两个三角形全等.
简记为 S.S.S.(或边边边)
导入新课
A
B
O
N
M
P
∟
∟
?
?
在△OMP和△ONP中
△OMP与△ONP全等吗?
????????=????????,??????????????????????????=????????,???????????????????∠????????????=∠????????????=????????°.
?
探讨角平分线的作法时,小明只带了直角三角板,他说只利用三角板也可以作角平分线,方法如下:
我们知道,证明三角形全等不存在SSA定理的.
思考:这个证明是否成立呢?这节课我们将讨论这个问题!!!
讲授新课
知识点一 利用“H.L.”判定直角三角形全等
舞台背景的形状是两个直角三角形,工作人员想知道两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住,无法测量.
(1) 你能帮他想个办法吗?
根据“S.A.S.”可测量其余两边与这两边的夹角.
根据“A.S.A.”,“A.A.S.”可测量对应一边和一锐角.
讲授新课
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等.于是,他就肯定“两个直角三角形是全等的”.
你相信这个结论吗?
(2)如果他只带一个卷尺,能完成这个任务吗?
下面,让我们来验证这个结论.
斜边和一条直角边对应相等→两个直角三角形全等?.
讲授新课
2 cm
3 cm
步骤:
1.画一条线段AB,使它等于2cm;
2.画∠MAB=90°(用量角器或三角尺);
3.以点B为圆心、3cm长为半径画圆弧,交射线AM于C;
△ABC即为所求.
M
A
B
C
把你画的直角三角形与其他同学画的直角三角形相比较,它们全等吗?
做一做
如图,已知两条线段,试画一个直角三角形,使长的线段为其斜边、短的线段为其一条直角边.
4.连结BC.
讲授新课
知识要点
“斜边直角边”判定方法
文字语言:
斜边和一条直角边分别相等的两个直角三角形全等
(简写成“斜边直角边”或“H.L.”).
几何语言:
A
B
C
A ′
B′
C ′
∴在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (H.L.).
∵∠C=∠C′=90°,
“S.S.A.”可以判定两个直角三角形全等,但是“边边”指的是斜边和一直角边,而“角”指的是直角.
AB=A′B′,
BC=B′C′,
讲授新课
典例精析
【例1】如图,已知 AC = BD,∠C = ∠D = 90°.求证: BC = AD.
证明: ∵∠C = ∠D = 90°(已知),
∴△ABC与△BAD 都是直角三角形(直角三角形的定义).
在Rt△ABC 与 Rt△BAD 中,
∵AB = BA (公共边),
AC = BD (已知),
∴Rt△ABC ≌ Rt△BAD (H.L.)
BC = AD (全等三角形的对应边相等).
讲授新课
1. 一般三角形的全等与直角三角形的全等是从一般到特殊的关系,二者之间的联系为: 一般三角形的判定方法同样适用于直角三角形.
2.判定一般三角形的全等与直角三角形的全等的区别:
(1)一般三角形全等的条件“S.S.S.”在直角三角形中被“H.L.”代替,无需找第三条边对应相等;
(2)“两边及其中一边的对角对应相等”不能判定一般三角形全等,但能判定直角三角形全等.
讲授新课
练一练
如图,在△ABC中,D为 BC 的中点,DE⊥AB,DF⊥AC,点 E、F 为垂足,DE = DF. 求证:△BED≌△CFD.
证明: ∵ DE ⊥ AB,DF ⊥ AC,
∴ ∠BED = ∠CFD = 90°,
∴△BED 与△CFD 都是直角三角形.
∵D 为 BC 的中点,
∴BD = CD .
在 Rt△BED 与 Rt△CFD 中,
∵BD = CD ,DE = DF,
∴Rt△BED ≌ Rt△CFD (H.L.).
讲授新课
2. 如图,AC = AD,∠C =∠D = 90°.求证: BC = BD.
证明:在Rt△ACB 和Rt△ADB 中,
∵AB=AB,AC=AD ,
∴Rt△ACB≌ Rt△ADB (H.L.).
∴BC = BD .
讲授新课
如图,有两个长度相同的滑梯,左边滑梯的高度 AC 与右边滑梯水平方向的跨度 DF 相等,两个滑梯的倾斜角∠B 与 ∠F 的大小有什么关系?说说你的想法和理由.
解: ∠B+∠F = 90°.
可以利用已知条件证明
Rt△ABC ≌ Rt△DEF (H.L.),
∴∠B =∠DEF,
∴∠B+∠F = 90°.
讲授新课
4. 如图,在△ABC中,AB = AC,AD是边 BC 上的高.
求证:(1)BD = DC;(2)∠BAD = ∠CAD.
证明: ∵AD 是 BC 边上的高,
∴∠ADB =∠ADC=90°.
在Rt△ADB 和Rt△ADC 中,
AB=AC,AD = AD,
∴Rt△ADB ≌ Rt△ADC (H.L.),
∴BD = DC,∠BAD =∠CAD .
讲授新课
5、一名工作人员不慎将一块三角形模具打碎成两块,他是否可以只带其中一块碎片到商店去,就能配一块与原来一样的三角形模具呢?他该带哪块去呢?请用数学知识解释你的结论.
解:可以.带右边的一块去.这样可以根据三角形全等的判定方法可知,具有全等的 3 个条件,即 A.S.A.
当堂检测
1、已知:如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°,
求证:②AO﹦BO,CO=DO.
A
D
C
B
②证明:在△AOC 和△BOD 中,
O
∠????=∠????已知,??????????????????∠????????????=∠????????????(对顶角相等),????????????=????????已证.??????????????????????
?
∴△AOC≌△BOD(AAS)
∴AO﹦BO,CO=DO(全等三角形对应边相等).
当堂检测
A
D
C
B
2.如图,AB⊥BD,CD⊥DB,AD=BC.求证:AB=CD,AD//BC.
证明:∵ AB⊥BD,CD⊥DB(已知),
∴∠ABD=∠CDB=90° (垂直定义).
在Rt△ABD和Rt△CDB中
????????=??????????(公共边)?,????????=????????(已知)?,???????
∴Rt△ABD≌Rt△CDB(HL).
∴∠ADB=∠CBD, AB=CD
(全等三角形对应边、对应角相等) .
∴ AD//BC(内错角相等,两直线平行) .
?
当堂检测
3.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,
AC=AE. 求证:BC=BE.
E
D
A
C
B
F
证明:∵ AD,AF分别是△ABC和△ABE的高,
∴∠ADB=∠AFB=90°
在Rt△ADC和Rt△AFE中, ????????=????????,????????=????????,?
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
在Rt△ADB和Rt△AFB中, ????????=????????,????????=????????,?
∴Rt△ADB≌Rt△AFB(HL).
∴BD=BF.
∴BD-CD=BF-EF.即BC=BE.
?
当堂检测
4. 如图所示,BE⊥AC,CF⊥AB,垂足分别是E、F.若BE=CF,则图中全等三角形有( )
A. 1对 B. 2对 C. 3对 D. 4对
C
A
F
C
B
E
根据全等的条件将全等的三角形一一列出即可;
当堂检测
5. 如图,已知AC⊥BD于点P,AP=CP,请增加一个条件,使△ABP≌△CDP(不能添加辅助线).
A
B
C
D
P
(1)若以“SAS”为依据,则可添加条件___________;
(2)若以“HL”为依据,则可添加条件___________ ;
(3)若以“ASA”为依据,则可添加条件__________ ;
(4)若以“AAS”为依据,则可添加条件___________.
BP=DP
AB=CD
∠A=∠C
∠B=∠D
当堂检测
6.如图,在四边形ABCD中,AB=AD,CA平分∠BCD,AE⊥BC于点E,AF⊥CD交CD的延长线于点F.
求证:△ABE≌△ADF.
A
D
C
B
F
E
证明:∵CA平分∠BCD,
∴∠ACE=∠ACF.
∵AE⊥BC于点E,AF⊥CD交CD的延长线于点F,
∴∠AEC=∠AFC=90°.
又∵AC=AC,
∴△ACE≌△ACF(AAS),
∴AE=AF.
在Rt△ABE和Rt△ADF中,
????????=????????,????????=????????,?
∴Rt△ABE≌Rt△ADF(HL).
?
当堂检测
7.如图,已知AD,BC相交于点O,AB=CD,AM⊥BC于点M,DN⊥BC于点N,BN=CM.
(1)求证:△ABM≌△DCN.
O
C
A
D
B
M
N
(1)证明:∵BN=CM
∴BN+MN=CM+MN,即:BM=CN,
∵AM⊥BC,DN⊥BC,
∴∠AMN=∠DNC=90°,
在Rt△ABM和Rt △ DCN中:
????????=????????,????????=????????,?
∴△ABM≌△DCN(HL);
?
当堂检测
O
C
A
D
B
M
N
(2)解:OA=OD,理由如下:
∵△ABM≌△DCN,
∴AM=DN,
在△AMO和△DNO中:
∠????????????=∠????????????=????????°,∠????????????=∠????????????,????????????=????????.??????????????????????
∴△AMO≌△DNO(AAS),
∴OA=OD.
?
(2)试猜想OA与OD的大小关系,并说明理由.
当堂检测
2.有一Rt△ABC,∠C=90°,AC=10cm,BC=5cm,线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AM上运动,问P点运动到AC上什么位置时,△ABC才能和△APQ全等?
B
C
A
P
Q
M
5cm
5cm
解:(1)当P运动到AP=BC时,
∵∠C=∠QAP=90°.
在Rt△ABC与Rt△QPA中,
????????=????????,????????=????????,??
∴Rt△ABC≌Rt△QPA(HL),
∴AP=BC=5cm;
?
第二种情况:
当堂检测
B
C
A
(P)
Q
M
10cm
5cm
(2)当P运动到与C点重合时,AP=AC.
在Rt△ABC与Rt△QPA中,
????????=????????,????????=????????,?
∴Rt△QAP≌Rt△BCA(HL),
∴AP=AC=10cm,
∴当AP=5cm或10cm时,
△ABC才能和△APQ全等.
?
第二种情况:
课堂小结
斜边直角边
判定定理
形式
斜边和一条直角边分别相等的两个直角三角形全等
H.L.(斜边直角边),存在于直角三角形中
判定直角三角形全等与判定一般三角形全等的联系与区别
应用
用H.L.解决问题
谢 谢~
