5.2 平行线(第3课时) 课件(共33张PPT)
文档属性
| 名称 | 5.2 平行线(第3课时) 课件(共33张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 08:29:06 | ||
图片预览








文档简介
数学(华东师大版)
七年级 上册
第5章 相交线与平行线
5.2 平行线
第3课时 平行线的性质
学习目标
1.掌握平行线的性质,会运用两条直线是平行判断角相等或互补;
2.能够根据平行线的性质进行简单的推理.
温故知新
两直线平行
1.同位角相等
2.内错角相等
3.同旁内角互补
问题 平行线的判定方法是什么?
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
导入新课
水下的潜艇通过潜望镜观察水面上的情况
潜望镜的原理如图所示,只要保证如图中所示两个平面镜平行放置,我们就可以看到下面直接看不到的情况了。
你能数学知识来解释吗?
讲授新课
知识点一 平行线的性质
7
1
2
3
4
5
6
8
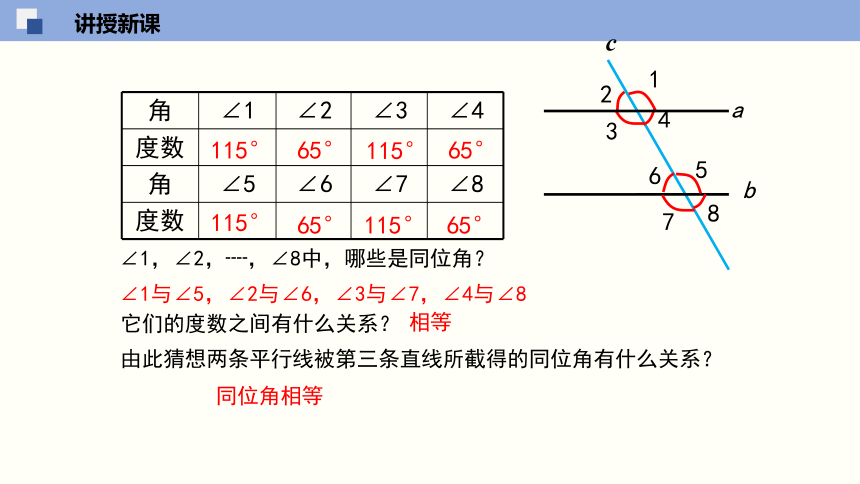
探究 画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角. 度量所形成的8个角的度数,把结果填入下表:
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
a
b
c
115°
115°
115°
115°
65°
65°
65°
65°
讲授新课
7
1
2
3
4
5
6
8
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
a
b
c
115°
115°
115°
115°
65°
65°
65°
65°
∠1,∠2,┈,∠8中,哪些是同位角?
它们的度数之间有什么关系?
由此猜想两条平行线被第三条直线所截得的同位角有什么关系?
∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8
相等
同位角相等
讲授新课
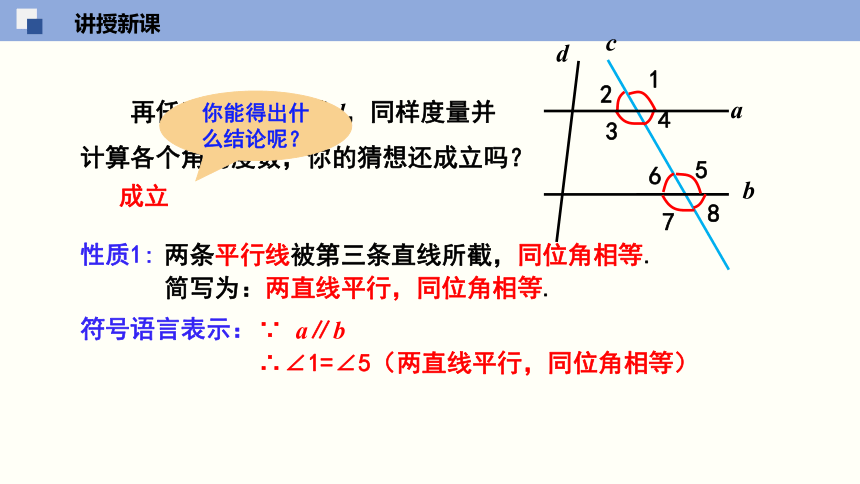
再任意画一条截线d,同样度量并计算各个角的度数,你的猜想还成立吗?
7
1
2
3
4
5
6
8
a
b
c
d
成立
你能得出什么结论呢?
性质1:
两条平行线被第三条直线所截,同位角相等.
简写为:两直线平行,同位角相等.
符号语言表示:
∵ a∥b
∴∠1=∠5(两直线平行,同位角相等)
讲授新课
思考:上一节中,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”,类似的,你能由性质1,推出两条平行线被第三条直线截得的内错角之间的关系吗?
如图,已知a//b,那么?1与?2相等吗?为什么?
∵a∥b(已知)
∴∠2=∠3 (两直线平行,同位角相等)
∵∠1=∠3 (对顶角相等)
∴∠1=∠2 (等量代换)
b
1
2
a
c
3
∠1=∠2 理由如下:
解:
你能得出什么结论呢?
讲授新课
性质2:
两条平行线被第三条直线所截,内错角相等.
简写为:两直线平行,内错角相等.
符号语言表示:
∵ a∥b
∴∠1=∠2(两直线平行,内错角相等)
b
1
2
a
c
3
讲授新课
如图,已知a//b,那么?2与?4有什么关系呢?为什么?
∴?2+?4=180°(等量代换)
思考:
类似的,已知两直线平行,能否得到同旁内角之间的数量关系?
? 2和?4互补.理由如下:
解:
b
1
2
a
c
3
∵a//b(已知)
∴?2=?3(两直线平行,同位角相等)
∵?3+?4=180°(邻补角定义)
4
你能得出什么结论呢?
讲授新课
b
1
2
a
c
3
4
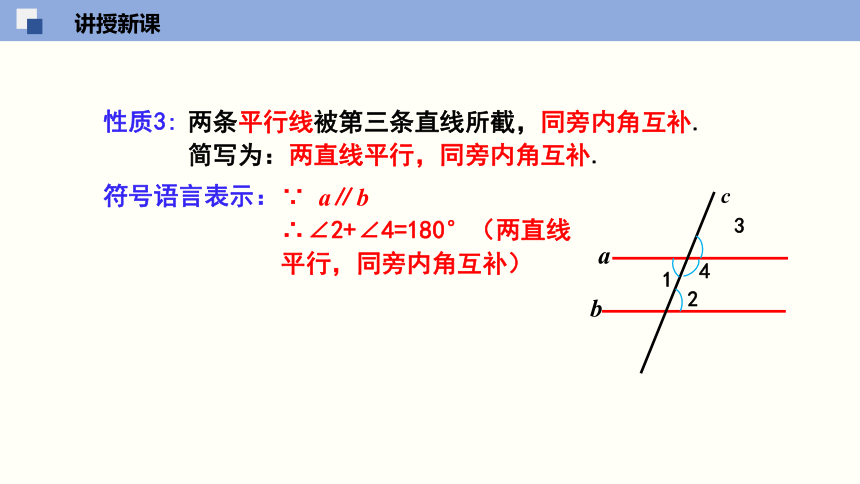
性质3:
两条平行线被第三条直线所截,同旁内角互补.
简写为:两直线平行,同旁内角互补.
符号语言表示:
∵ a∥b
∴∠2+∠4=180°(两直线平行,同旁内角互补)
讲授新课
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
讨论:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?(分组讨论)
讲授新课
平行线的性质:
1. 两直线平行,同位角相等.
2. 两直线平行,内错角相等.
3. 两直线平行,同旁内角互补.
知识概括
讲授新课
典例精析
【例1】如图,AB∥CD直角三角尺的直角顶点在CD上,如果∠1=28°,那么∠2的度数为(????)
A.28° B.62° C.56° D.72°
讲授新课
【详解】解:如图:
∵∠EFG=90°,∠1=28°,
∠3=∠EFG-∠1=62°
∵AB∥CD,
∴∠2=∠3=62°
故选:B.
讲授新课
【例2】如图,直线a∥b,一块含60°角的直角三角板如图放置,若∠1=13°,则∠2的度数为(????).
A.45° B.47° C.55° D.57°
讲授新课
【详解】过点B作BD∥a,
∴∠CBD=∠2,
∵a∥b,
∴BD∥b,
又∵∠1=13°,
∴∠1=∠ABD=13°,
∵∠ABC=60°,
∴∠DBC=60°-13°=47°,
∴∠2=47°.
故选:B.
讲授新课
【例3】如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于(????)
A.50° B.60° C.65° D.90°
讲授新课
【详解】解:∵AB∥CD,
∴∠BEF+∠1=180°,
∵∠1=50°,
∴∠BEF=130°,
∵EG平分∠BEF,
∴∠BEG=12∠????????????=65°,
∴∠2=∠BEG=65°,
故选:C.
?
讲授新课
练一练
1.如图,直线a,b被直线l所截,如果a∥b,∠1=120°,那么∠2=___________度.
【详解】解:∵a∥b,∠1=120°,
∴∠3=∠1=120°,
∴∠2=180°-120°=60°.
故答案为:60.
讲授新课
2.如图,AB∥CD∥EF,∠A=54°,∠C=26°,则∠AFC=________ .
【详解】解:∵AB∥EF,∠A=54°,
∴∠A=∠AEF=54°,
∵CD∥EF,∠C=26°,
∴∠C=∠CFE=26°,
∴∠AFC=∠AFE-∠CFE=28°,
故答案为:28°.
讲授新课
3.如图,已知AB∥CD,∠B=150°,∠D=130°,那么∠E=_____度.
【详解】解:过点E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠1+∠B=180°,∠2+∠D=180°,
∵∠B=150°,∠D=130°,
∴∠1=30°,∠2=50°,
∴∠BED=∠1+∠2=80°.
故答案为:80.
当堂检测
1. 如图,若AB∥CD,则下列结论一定成立的是( )
A.∠1=∠2
B. AD∥BC
C. ∠B=∠D
D. ∠3=∠4
D
当堂检测
2.如图,已知CD∥BE,∠1=68°,那么∠B的度数为( )
A. 68°
B. 102°
C. 110°
D. 112°
D
当堂检测
3.如图,若∠A+∠ABC=180°,则下列结论正确的是( )
A.∠1=∠2
B. ∠2=∠3
C. ∠1=∠3
D. ∠2=∠4
D
当堂检测
4. 一小区大门的栏杆如图,当栏杆抬起时,BA垂直于地面AE,CD平行于地面AE,则∠ABC+∠BCD的度数为( )
A. 180° B. 270° C. 300° D. 360°
B
当堂检测
5. 如图,已知∠A=∠1,∠C=∠F.求证:BC∥EF.
证明:∵∠A=∠1(已知)
∴AC∥DF(同位角相等,两直线平行)
∴∠C=∠BGD(两直线平行,同位角相等)
又∵∠C=∠F(已知)
∴∠BGD=∠F(等量代换)
∴BC∥EF(同位角相等,两直线平行)
当堂检测
∴∠ABD=∠BDC(两直线平行,内错角相等)
证明:∵AB∥CD(已知)
∵AE∥BD( 已知)
∴∠BDC=∠E (两直线平行,同位角相等)
∴∠ABD=∠E(等量代换)
6.如图,已知:AB∥CD,AE∥BD,试说明∠ABD=∠E.
当堂检测
7. 如图,已知AD∥BC,∠1=∠2,试说明:∠3+∠4=180°.
解:因为AD∥BC(已知),
所以∠1=∠3(两直线平行,内错角相等).
因为∠1=∠2(已知),
所以∠2=∠3(等量代换).
所以BE∥DF(同位角相等,两直线平行).
所以∠3+∠4=180°(两直线平行,同旁内角互补).
当堂检测
8.如图,已知点A、D在直线EF上,∠1+∠2=180°,DB平分∠ADC,AD∥BC.
(1)求证:AB∥DC ;
(2)若∠DAB=128°,求∠DBC的度数.
当堂检测
【详解】(1)证明:∵∠1+∠2=180°,∠1+∠DAB=180°,∠2+∠ADC=180°
∴∠BAD+∠CDA=180°,
∴AB∥DC;
(2)解:∵∠BAD+∠CDA=180°,∠DAB=128°,
∴∠ADC=180°-128°=52°,
∵DB平分∠ADC,
∴∠ADB=∠BDC=12∠????????????=26°,
∵AD∥BC,
∴∠DBC=∠ADB=26°.
?
课堂小结
平行线的性质
平行线的判定
平行线的性质
性质1:两直线平行,同位角相等
性质2:两直线平行,内错角相等
性质3:两直线平行,同旁内角互补
应用:求角的度数,说明角相等或互补
互逆
谢 谢~
七年级 上册
第5章 相交线与平行线
5.2 平行线
第3课时 平行线的性质
学习目标
1.掌握平行线的性质,会运用两条直线是平行判断角相等或互补;
2.能够根据平行线的性质进行简单的推理.
温故知新
两直线平行
1.同位角相等
2.内错角相等
3.同旁内角互补
问题 平行线的判定方法是什么?
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
导入新课
水下的潜艇通过潜望镜观察水面上的情况
潜望镜的原理如图所示,只要保证如图中所示两个平面镜平行放置,我们就可以看到下面直接看不到的情况了。
你能数学知识来解释吗?
讲授新课
知识点一 平行线的性质
7
1
2
3
4
5
6
8
探究 画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角. 度量所形成的8个角的度数,把结果填入下表:
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
a
b
c
115°
115°
115°
115°
65°
65°
65°
65°
讲授新课
7
1
2
3
4
5
6
8
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
a
b
c
115°
115°
115°
115°
65°
65°
65°
65°
∠1,∠2,┈,∠8中,哪些是同位角?
它们的度数之间有什么关系?
由此猜想两条平行线被第三条直线所截得的同位角有什么关系?
∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8
相等
同位角相等
讲授新课
再任意画一条截线d,同样度量并计算各个角的度数,你的猜想还成立吗?
7
1
2
3
4
5
6
8
a
b
c
d
成立
你能得出什么结论呢?
性质1:
两条平行线被第三条直线所截,同位角相等.
简写为:两直线平行,同位角相等.
符号语言表示:
∵ a∥b
∴∠1=∠5(两直线平行,同位角相等)
讲授新课
思考:上一节中,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”,类似的,你能由性质1,推出两条平行线被第三条直线截得的内错角之间的关系吗?
如图,已知a//b,那么?1与?2相等吗?为什么?
∵a∥b(已知)
∴∠2=∠3 (两直线平行,同位角相等)
∵∠1=∠3 (对顶角相等)
∴∠1=∠2 (等量代换)
b
1
2
a
c
3
∠1=∠2 理由如下:
解:
你能得出什么结论呢?
讲授新课
性质2:
两条平行线被第三条直线所截,内错角相等.
简写为:两直线平行,内错角相等.
符号语言表示:
∵ a∥b
∴∠1=∠2(两直线平行,内错角相等)
b
1
2
a
c
3
讲授新课
如图,已知a//b,那么?2与?4有什么关系呢?为什么?
∴?2+?4=180°(等量代换)
思考:
类似的,已知两直线平行,能否得到同旁内角之间的数量关系?
? 2和?4互补.理由如下:
解:
b
1
2
a
c
3
∵a//b(已知)
∴?2=?3(两直线平行,同位角相等)
∵?3+?4=180°(邻补角定义)
4
你能得出什么结论呢?
讲授新课
b
1
2
a
c
3
4
性质3:
两条平行线被第三条直线所截,同旁内角互补.
简写为:两直线平行,同旁内角互补.
符号语言表示:
∵ a∥b
∴∠2+∠4=180°(两直线平行,同旁内角互补)
讲授新课
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
讨论:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?(分组讨论)
讲授新课
平行线的性质:
1. 两直线平行,同位角相等.
2. 两直线平行,内错角相等.
3. 两直线平行,同旁内角互补.
知识概括
讲授新课
典例精析
【例1】如图,AB∥CD直角三角尺的直角顶点在CD上,如果∠1=28°,那么∠2的度数为(????)
A.28° B.62° C.56° D.72°
讲授新课
【详解】解:如图:
∵∠EFG=90°,∠1=28°,
∠3=∠EFG-∠1=62°
∵AB∥CD,
∴∠2=∠3=62°
故选:B.
讲授新课
【例2】如图,直线a∥b,一块含60°角的直角三角板如图放置,若∠1=13°,则∠2的度数为(????).
A.45° B.47° C.55° D.57°
讲授新课
【详解】过点B作BD∥a,
∴∠CBD=∠2,
∵a∥b,
∴BD∥b,
又∵∠1=13°,
∴∠1=∠ABD=13°,
∵∠ABC=60°,
∴∠DBC=60°-13°=47°,
∴∠2=47°.
故选:B.
讲授新课
【例3】如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于(????)
A.50° B.60° C.65° D.90°
讲授新课
【详解】解:∵AB∥CD,
∴∠BEF+∠1=180°,
∵∠1=50°,
∴∠BEF=130°,
∵EG平分∠BEF,
∴∠BEG=12∠????????????=65°,
∴∠2=∠BEG=65°,
故选:C.
?
讲授新课
练一练
1.如图,直线a,b被直线l所截,如果a∥b,∠1=120°,那么∠2=___________度.
【详解】解:∵a∥b,∠1=120°,
∴∠3=∠1=120°,
∴∠2=180°-120°=60°.
故答案为:60.
讲授新课
2.如图,AB∥CD∥EF,∠A=54°,∠C=26°,则∠AFC=________ .
【详解】解:∵AB∥EF,∠A=54°,
∴∠A=∠AEF=54°,
∵CD∥EF,∠C=26°,
∴∠C=∠CFE=26°,
∴∠AFC=∠AFE-∠CFE=28°,
故答案为:28°.
讲授新课
3.如图,已知AB∥CD,∠B=150°,∠D=130°,那么∠E=_____度.
【详解】解:过点E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠1+∠B=180°,∠2+∠D=180°,
∵∠B=150°,∠D=130°,
∴∠1=30°,∠2=50°,
∴∠BED=∠1+∠2=80°.
故答案为:80.
当堂检测
1. 如图,若AB∥CD,则下列结论一定成立的是( )
A.∠1=∠2
B. AD∥BC
C. ∠B=∠D
D. ∠3=∠4
D
当堂检测
2.如图,已知CD∥BE,∠1=68°,那么∠B的度数为( )
A. 68°
B. 102°
C. 110°
D. 112°
D
当堂检测
3.如图,若∠A+∠ABC=180°,则下列结论正确的是( )
A.∠1=∠2
B. ∠2=∠3
C. ∠1=∠3
D. ∠2=∠4
D
当堂检测
4. 一小区大门的栏杆如图,当栏杆抬起时,BA垂直于地面AE,CD平行于地面AE,则∠ABC+∠BCD的度数为( )
A. 180° B. 270° C. 300° D. 360°
B
当堂检测
5. 如图,已知∠A=∠1,∠C=∠F.求证:BC∥EF.
证明:∵∠A=∠1(已知)
∴AC∥DF(同位角相等,两直线平行)
∴∠C=∠BGD(两直线平行,同位角相等)
又∵∠C=∠F(已知)
∴∠BGD=∠F(等量代换)
∴BC∥EF(同位角相等,两直线平行)
当堂检测
∴∠ABD=∠BDC(两直线平行,内错角相等)
证明:∵AB∥CD(已知)
∵AE∥BD( 已知)
∴∠BDC=∠E (两直线平行,同位角相等)
∴∠ABD=∠E(等量代换)
6.如图,已知:AB∥CD,AE∥BD,试说明∠ABD=∠E.
当堂检测
7. 如图,已知AD∥BC,∠1=∠2,试说明:∠3+∠4=180°.
解:因为AD∥BC(已知),
所以∠1=∠3(两直线平行,内错角相等).
因为∠1=∠2(已知),
所以∠2=∠3(等量代换).
所以BE∥DF(同位角相等,两直线平行).
所以∠3+∠4=180°(两直线平行,同旁内角互补).
当堂检测
8.如图,已知点A、D在直线EF上,∠1+∠2=180°,DB平分∠ADC,AD∥BC.
(1)求证:AB∥DC ;
(2)若∠DAB=128°,求∠DBC的度数.
当堂检测
【详解】(1)证明:∵∠1+∠2=180°,∠1+∠DAB=180°,∠2+∠ADC=180°
∴∠BAD+∠CDA=180°,
∴AB∥DC;
(2)解:∵∠BAD+∠CDA=180°,∠DAB=128°,
∴∠ADC=180°-128°=52°,
∵DB平分∠ADC,
∴∠ADB=∠BDC=12∠????????????=26°,
∵AD∥BC,
∴∠DBC=∠ADB=26°.
?
课堂小结
平行线的性质
平行线的判定
平行线的性质
性质1:两直线平行,同位角相等
性质2:两直线平行,内错角相等
性质3:两直线平行,同旁内角互补
应用:求角的度数,说明角相等或互补
互逆
谢 谢~
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
