13.5 逆命题与逆定理(第3课时) 课件(共28张PPT)
文档属性
| 名称 | 13.5 逆命题与逆定理(第3课时) 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 08:33:39 | ||
图片预览





文档简介
数学(华东师大版)
八年级 上册
13.5 逆命题与逆定理
第3课时 角平分线
第13章 全等三角形
学习目标
1、会叙述角平分线的性质及判定;
2、能利用三角形全等,证明角平分线的性质定理,理解和掌握角平分线性质定理和它的逆定理.能应用这两个性质解决一些简单的实际问题;
3、经历探索、猜想、证明的过程,进一步发展学生的推理证明意识和能力.
温故知新
如图,你能画出∠AOB的对称轴吗?
射线OC就是的∠AOB的对称轴,也是角平分线.
A
O
B
C
导入新课
在一个三角形居住区内修有一个学校P,P到AB、BC、CA三边的距离都相等,请在三角形居住区内标出学校P的位置,P在何处?
A
B
C
问题情境
讲授新课
知识点一 角平分线的性质定理
如图,点P是∠AOB的角平分线OC上的任意一点,且PD⊥OA于点D,PE⊥OB于点E,将∠AOB沿OC对折,你发现了什么?如何表达,并简述你的证明过程.
对折后PD、PE能够完全重合,PD=PE.
角是轴对称图形吗?它的对称轴是什么?
D
P
A
C
B
E
O
讲授新课
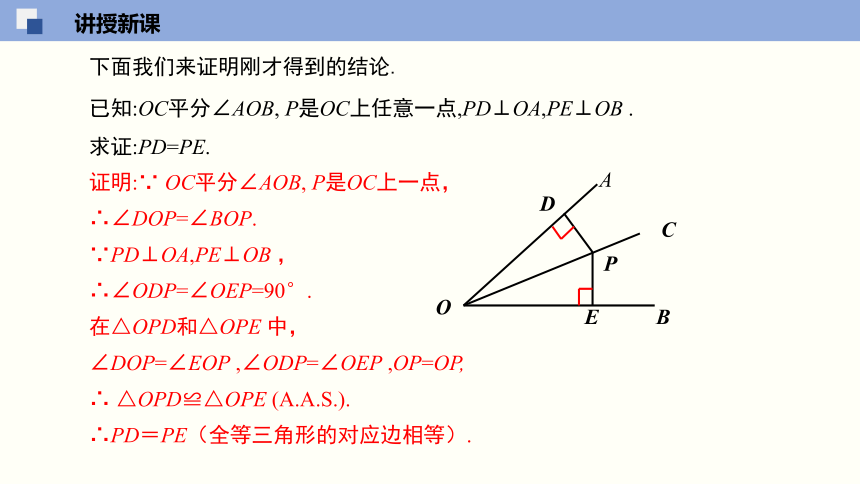
下面我们来证明刚才得到的结论.
D
P
A
C
B
E
O
已知:OC平分∠AOB, P是OC上任意一点,PD⊥OA,PE⊥OB .
求证:PD=PE.
证明:∵ OC平分∠AOB, P是OC上一点,
∴∠DOP=∠BOP.
∵PD⊥OA,PE⊥OB ,
∴∠ODP=∠OEP=90°.
在△OPD和△OPE 中,
∠DOP=∠EOP ,∠ODP=∠OEP ,OP=OP,
∴ △OPD≌△OPE (A.A.S.).
∴PD=PE(全等三角形的对应边相等).
讲授新课
由上面证明,我们得到角平分线的性质定理:
角平分线上的点到角两边的距离相等.
几何语言描述:
∵ OC平分∠AOB,
且PD⊥OA, PE⊥OB.
∴ PD= PE.
应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
定理的作用:
证明线段相等.
讲授新课
典例精析
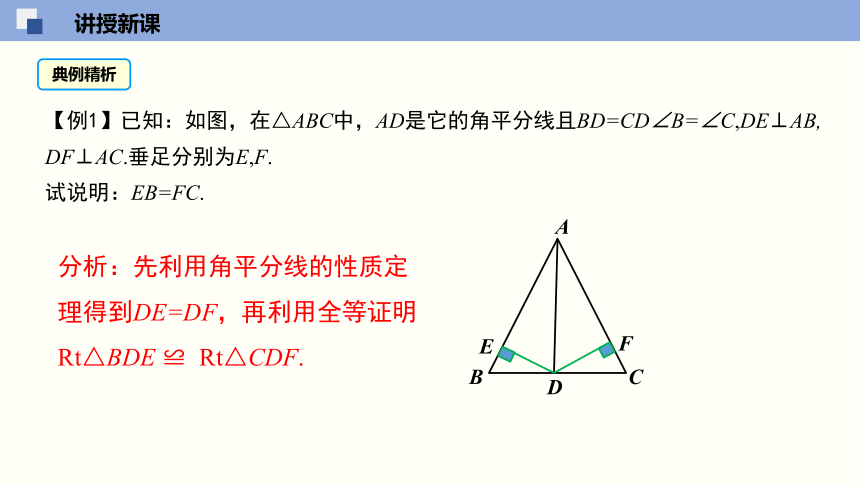
【例1】已知:如图,在△ABC中,AD是它的角平分线且BD=CD∠B=∠C,DE⊥AB, DF⊥AC.垂足分别为E,F.
试说明:EB=FC.
A
B
C
D
E
F
分析:先利用角平分线的性质定理得到DE=DF,再利用全等证明Rt△BDE ≌ Rt△CDF.
讲授新课
A
B
C
D
E
F
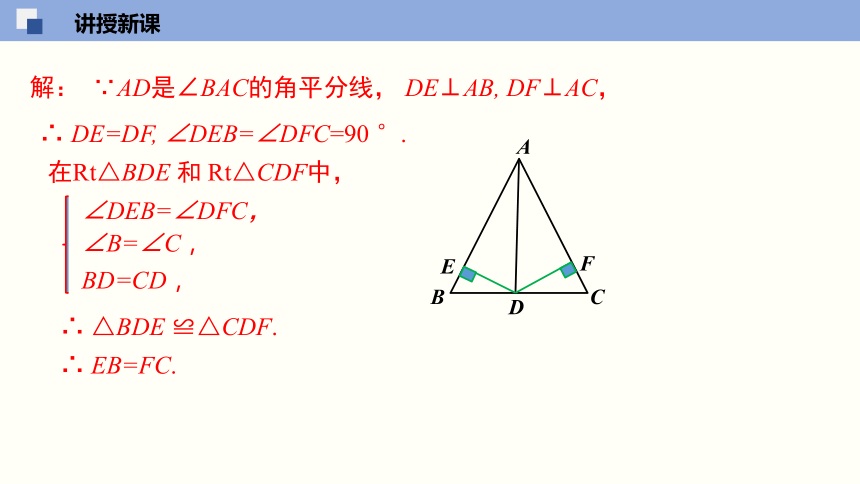
解: ∵AD是∠BAC的角平分线, DE⊥AB, DF⊥AC,
∴ DE=DF, ∠DEB=∠DFC=90 °.
在Rt△BDE 和 Rt△CDF中,
∴ △BDE ≌△CDF.
∴ EB=FC.
BD=CD,
∠B=∠C,
∠DEB=∠DFC,
讲授新课
练一练
(1)∵ 如图,AD平分∠BAC(已知)
∴ = ,( ).
角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
1、判断下列的写法是否正确?
理由:
没有垂直,不能确定BD、CD是点D到角两边的距离.
讲授新课
(2)∵ 如图, DC⊥AC,DB⊥AB (已知).
∴ = ,
( )
角内任意一条线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
理由:
无法确定点D在∠BAC的平分线上.
在角平分线上和垂直这两个条件缺一不可.
讲授新课
知识点二 角平分线的判定定理
这一定理描述了角平分线的性质,那么反过来会有什么结果呢?
写出性质定理及其逆命题的条件和结论,你有什么发现?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
t条 件
结 论
性质定理
逆命题
一个点在角的平分线上
这个点到这个角两边的距离相等
一个点到角两边的距离相等
这个点在这个角的平分线上
想想看,这个逆命题是否是一个真命题?你能证明吗?
讲授新课
逆命题 如果一个点到角两边的距离相等,那么这个点在这个角的平分线上.
分析:为了证明点P在∠AOB的平分线上,可以先作射线OP,然后证明Rt△PDO≌Rt△PEO,从而得到∠AOP=∠BOP.
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE.
求证:点P在∠AOB的角平分线上.
B
A
D
O
P
E
讲授新课
证明:
作射线OP,
在Rt△PDO和Rt△PEO 中,
(全等三角形的对应角相等).
OP=OP(公共边),
PD= PE(已知),
∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°,
∴Rt△PDO≌Rt△PEO( H.L.).
∴∠AOP=∠BOP
B
A
D
O
P
E
∴点P在∠AOB的平分线上.
讲授新课
判定定理:
角的内部到角两边距离相等的点在角的平分线上.
应用所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边距离相等.
定理的作用:判断点在角平分线上.
应用格式:
∵ PD⊥OA,PE⊥OB,PD=PE,
∴点P 在∠AOB的平分线上.
D
P
A
C
B
E
O
角平分线的判定定理与性质定理互为逆定理.
讲授新课
利用尺规作三角形的三条角平分线,你发现了什么?
发现:三角形的三条角平分线交于一点.
做一做
怎样证明这个结论呢?
A
B
C
P
N
M
讲授新课
点拨:要证明三角形的三条角平分线相交于一点,只要证明其中两条角平分线的交点一定在第三条角平分线上即可.思路可表示如下:
试试看,你会写出证明过程吗?
AP是∠BAC的平分线
BP是∠ABC的平分线
PI=PH
PG=PI
PH=PG
点P在∠BCA的平分线上
A
B
C
P
F
H
D
E
I
G
讲授新课
典例精析
【例2】如图,BD⊥AC,CE⊥AB,垂足分别为点D和点E,BD与CE相交于点F,BF=CF. 求证:点F在∠BAC的平分线上.
证明:∵BD⊥AC,CE⊥AB,
∴∠CDF=∠BEF=90 °.
在△CDF和△BEF中,
∵∠CDF=∠BEF=90 °,∠CFD=∠BFE,BF=CF,
∴△CDF≌△BEF( A.A.S.),
∴DF=EF,
∴点F在∠BAC的平分线上.
A
B
C
D
F
E
讲授新课
练一练
1.如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F. 求证:点F在∠DAE的平分线上.
A
B
C
D
E
F
证明:作FG⊥AC,FH⊥BC,FM⊥AB﹐垂足分别为G、H 、M .
G
H
M
∵ CF平分∠ECB,BF平分∠CBD
∴ FG=FH=FM
∴点F在∠DAE的平分线上.
讲授新课
2、如图所示,在△ABC中,BD=CD,∠ABD=∠ACD.
求证:AD平分∠BAC.
A
B
C
D
M
N
证明:如图,过点D作DM⊥AB于点M,DN⊥AC于点N,则∠BMD=∠CND=90°.在△BDM和△CDN中,
∠????????????=∠????????????,∠????????????=∠????????????,????????=????????,
∴△BDM≌△CDN(AAS).
∴DM=DN.又∵DM⊥AB,DN⊥AC,
∴AD平分∠BAC.
?
当堂检测
1. 如图,P是∠AOB的平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
A.2 B.3 C. 1 D.4
D
E
O
B
A
●
D
P
C
当堂检测
2. 如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.
下列结论中不一定成立的是( )
A.PA=PB B.PO平分∠APB
C.OA=OB D.AB垂直平分OP
D
O
●
B
P
A
当堂检测
3.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,若AB=6 cm,则△DBE的周长是_____
6 cm
A
C
D
B
E
当堂检测
4.如图,AD为△ABC的角平分线,DF⊥AC于点F,∠B=90°,DE=DC.
求证:BE=FC.
B
A
D
C
E
F
证明:∵∠B=90°,
∴BD⊥AB.又∵AD为△ABC的角平分线,且DF⊥AC,
∴DB=DF.在Rt△BDE和Rt△FDC中,
????????=????????,????????=????????,
∴Rt△BDE≌Rt△FDC(HL).∴BE=FC.
?
当堂检测
5、已知:如图,P是OC上一点,PD⊥OA于点D,PE⊥OB于点E,F、G分别是OA、OB上的点,且PF=PG,DF=EG.
求证:OC是∠AOB的平分线.
O
B
A
E
C
D
P
F
G
证明:∵PD⊥OA,PE⊥OB,
∴∠PDF=∠PEG=90°.
在Rt△PFD和Rt△PGE中,
????????=????????,????????=????????,
∴Rt△PFD≌Rt△PGE(HL),
∴PD=PE.
∵P是OC上点,PD⊥OA,PE⊥OB,
∴OC是∠AOB的平分线.
?
当堂检测
6.已知:如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上,BD=DF.
求证:CF=EB.
证明:∵AD平分∠CAB,
DE⊥AB,∠C=90°(已知),
∴ CD=DE (角平分线的性质).
在Rt△CDF和Rt△EDB中,
CD=ED(已证),
DF=DB (已知),
∴ Rt△CDF≌Rt△EDB (H.L.).
∴ CF=EB(全等三角形的对应边相等).
C
F
A
E
D
B
课堂小结
角平分线的性质及判定
性质定理:角平分线上的点到角两边的距离相等.
判定定理:角的内部到角两边距离相等的点在角的平分线上.
谢 谢~
八年级 上册
13.5 逆命题与逆定理
第3课时 角平分线
第13章 全等三角形
学习目标
1、会叙述角平分线的性质及判定;
2、能利用三角形全等,证明角平分线的性质定理,理解和掌握角平分线性质定理和它的逆定理.能应用这两个性质解决一些简单的实际问题;
3、经历探索、猜想、证明的过程,进一步发展学生的推理证明意识和能力.
温故知新
如图,你能画出∠AOB的对称轴吗?
射线OC就是的∠AOB的对称轴,也是角平分线.
A
O
B
C
导入新课
在一个三角形居住区内修有一个学校P,P到AB、BC、CA三边的距离都相等,请在三角形居住区内标出学校P的位置,P在何处?
A
B
C
问题情境
讲授新课
知识点一 角平分线的性质定理
如图,点P是∠AOB的角平分线OC上的任意一点,且PD⊥OA于点D,PE⊥OB于点E,将∠AOB沿OC对折,你发现了什么?如何表达,并简述你的证明过程.
对折后PD、PE能够完全重合,PD=PE.
角是轴对称图形吗?它的对称轴是什么?
D
P
A
C
B
E
O
讲授新课
下面我们来证明刚才得到的结论.
D
P
A
C
B
E
O
已知:OC平分∠AOB, P是OC上任意一点,PD⊥OA,PE⊥OB .
求证:PD=PE.
证明:∵ OC平分∠AOB, P是OC上一点,
∴∠DOP=∠BOP.
∵PD⊥OA,PE⊥OB ,
∴∠ODP=∠OEP=90°.
在△OPD和△OPE 中,
∠DOP=∠EOP ,∠ODP=∠OEP ,OP=OP,
∴ △OPD≌△OPE (A.A.S.).
∴PD=PE(全等三角形的对应边相等).
讲授新课
由上面证明,我们得到角平分线的性质定理:
角平分线上的点到角两边的距离相等.
几何语言描述:
∵ OC平分∠AOB,
且PD⊥OA, PE⊥OB.
∴ PD= PE.
应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
定理的作用:
证明线段相等.
讲授新课
典例精析
【例1】已知:如图,在△ABC中,AD是它的角平分线且BD=CD∠B=∠C,DE⊥AB, DF⊥AC.垂足分别为E,F.
试说明:EB=FC.
A
B
C
D
E
F
分析:先利用角平分线的性质定理得到DE=DF,再利用全等证明Rt△BDE ≌ Rt△CDF.
讲授新课
A
B
C
D
E
F
解: ∵AD是∠BAC的角平分线, DE⊥AB, DF⊥AC,
∴ DE=DF, ∠DEB=∠DFC=90 °.
在Rt△BDE 和 Rt△CDF中,
∴ △BDE ≌△CDF.
∴ EB=FC.
BD=CD,
∠B=∠C,
∠DEB=∠DFC,
讲授新课
练一练
(1)∵ 如图,AD平分∠BAC(已知)
∴ = ,( ).
角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
1、判断下列的写法是否正确?
理由:
没有垂直,不能确定BD、CD是点D到角两边的距离.
讲授新课
(2)∵ 如图, DC⊥AC,DB⊥AB (已知).
∴ = ,
( )
角内任意一条线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
理由:
无法确定点D在∠BAC的平分线上.
在角平分线上和垂直这两个条件缺一不可.
讲授新课
知识点二 角平分线的判定定理
这一定理描述了角平分线的性质,那么反过来会有什么结果呢?
写出性质定理及其逆命题的条件和结论,你有什么发现?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
t条 件
结 论
性质定理
逆命题
一个点在角的平分线上
这个点到这个角两边的距离相等
一个点到角两边的距离相等
这个点在这个角的平分线上
想想看,这个逆命题是否是一个真命题?你能证明吗?
讲授新课
逆命题 如果一个点到角两边的距离相等,那么这个点在这个角的平分线上.
分析:为了证明点P在∠AOB的平分线上,可以先作射线OP,然后证明Rt△PDO≌Rt△PEO,从而得到∠AOP=∠BOP.
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE.
求证:点P在∠AOB的角平分线上.
B
A
D
O
P
E
讲授新课
证明:
作射线OP,
在Rt△PDO和Rt△PEO 中,
(全等三角形的对应角相等).
OP=OP(公共边),
PD= PE(已知),
∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°,
∴Rt△PDO≌Rt△PEO( H.L.).
∴∠AOP=∠BOP
B
A
D
O
P
E
∴点P在∠AOB的平分线上.
讲授新课
判定定理:
角的内部到角两边距离相等的点在角的平分线上.
应用所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边距离相等.
定理的作用:判断点在角平分线上.
应用格式:
∵ PD⊥OA,PE⊥OB,PD=PE,
∴点P 在∠AOB的平分线上.
D
P
A
C
B
E
O
角平分线的判定定理与性质定理互为逆定理.
讲授新课
利用尺规作三角形的三条角平分线,你发现了什么?
发现:三角形的三条角平分线交于一点.
做一做
怎样证明这个结论呢?
A
B
C
P
N
M
讲授新课
点拨:要证明三角形的三条角平分线相交于一点,只要证明其中两条角平分线的交点一定在第三条角平分线上即可.思路可表示如下:
试试看,你会写出证明过程吗?
AP是∠BAC的平分线
BP是∠ABC的平分线
PI=PH
PG=PI
PH=PG
点P在∠BCA的平分线上
A
B
C
P
F
H
D
E
I
G
讲授新课
典例精析
【例2】如图,BD⊥AC,CE⊥AB,垂足分别为点D和点E,BD与CE相交于点F,BF=CF. 求证:点F在∠BAC的平分线上.
证明:∵BD⊥AC,CE⊥AB,
∴∠CDF=∠BEF=90 °.
在△CDF和△BEF中,
∵∠CDF=∠BEF=90 °,∠CFD=∠BFE,BF=CF,
∴△CDF≌△BEF( A.A.S.),
∴DF=EF,
∴点F在∠BAC的平分线上.
A
B
C
D
F
E
讲授新课
练一练
1.如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F. 求证:点F在∠DAE的平分线上.
A
B
C
D
E
F
证明:作FG⊥AC,FH⊥BC,FM⊥AB﹐垂足分别为G、H 、M .
G
H
M
∵ CF平分∠ECB,BF平分∠CBD
∴ FG=FH=FM
∴点F在∠DAE的平分线上.
讲授新课
2、如图所示,在△ABC中,BD=CD,∠ABD=∠ACD.
求证:AD平分∠BAC.
A
B
C
D
M
N
证明:如图,过点D作DM⊥AB于点M,DN⊥AC于点N,则∠BMD=∠CND=90°.在△BDM和△CDN中,
∠????????????=∠????????????,∠????????????=∠????????????,????????=????????,
∴△BDM≌△CDN(AAS).
∴DM=DN.又∵DM⊥AB,DN⊥AC,
∴AD平分∠BAC.
?
当堂检测
1. 如图,P是∠AOB的平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
A.2 B.3 C. 1 D.4
D
E
O
B
A
●
D
P
C
当堂检测
2. 如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.
下列结论中不一定成立的是( )
A.PA=PB B.PO平分∠APB
C.OA=OB D.AB垂直平分OP
D
O
●
B
P
A
当堂检测
3.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,若AB=6 cm,则△DBE的周长是_____
6 cm
A
C
D
B
E
当堂检测
4.如图,AD为△ABC的角平分线,DF⊥AC于点F,∠B=90°,DE=DC.
求证:BE=FC.
B
A
D
C
E
F
证明:∵∠B=90°,
∴BD⊥AB.又∵AD为△ABC的角平分线,且DF⊥AC,
∴DB=DF.在Rt△BDE和Rt△FDC中,
????????=????????,????????=????????,
∴Rt△BDE≌Rt△FDC(HL).∴BE=FC.
?
当堂检测
5、已知:如图,P是OC上一点,PD⊥OA于点D,PE⊥OB于点E,F、G分别是OA、OB上的点,且PF=PG,DF=EG.
求证:OC是∠AOB的平分线.
O
B
A
E
C
D
P
F
G
证明:∵PD⊥OA,PE⊥OB,
∴∠PDF=∠PEG=90°.
在Rt△PFD和Rt△PGE中,
????????=????????,????????=????????,
∴Rt△PFD≌Rt△PGE(HL),
∴PD=PE.
∵P是OC上点,PD⊥OA,PE⊥OB,
∴OC是∠AOB的平分线.
?
当堂检测
6.已知:如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上,BD=DF.
求证:CF=EB.
证明:∵AD平分∠CAB,
DE⊥AB,∠C=90°(已知),
∴ CD=DE (角平分线的性质).
在Rt△CDF和Rt△EDB中,
CD=ED(已证),
DF=DB (已知),
∴ Rt△CDF≌Rt△EDB (H.L.).
∴ CF=EB(全等三角形的对应边相等).
C
F
A
E
D
B
课堂小结
角平分线的性质及判定
性质定理:角平分线上的点到角两边的距离相等.
判定定理:角的内部到角两边距离相等的点在角的平分线上.
谢 谢~
