13.4 尺规作图(第1课时) 课件(共31张PPT)
文档属性
| 名称 | 13.4 尺规作图(第1课时) 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 09:42:29 | ||
图片预览







文档简介
(共31张PPT)
13.4 尺规作图
第1课时
数学(华东师大版)
八年级 上册
第13章 全等三角形
学习目标
1、了解尺规作图的定义,会用尺规:(1)作一条线段等于已知线段;(2)作一个角等于已知角;(3)作已知角的平分线;
2、应用三角形全等的知识,解释角平分线的原理;
3、会用尺规作一个三角形;培养学生动手能力,会说求作过程.
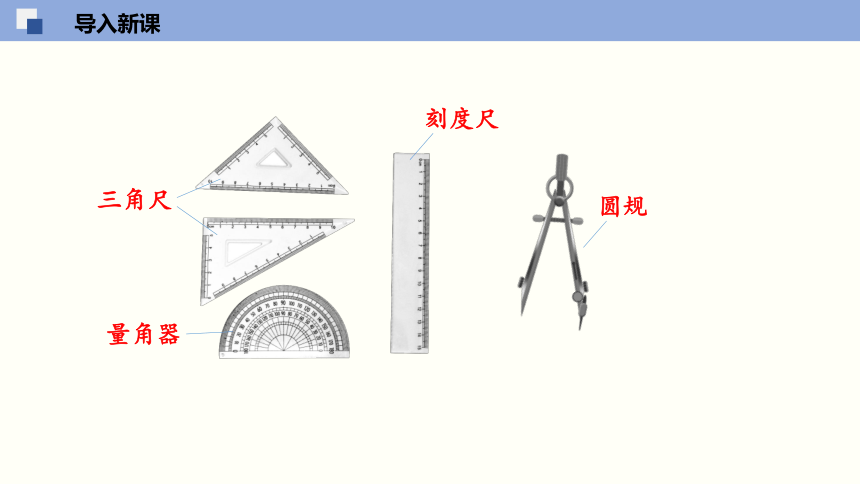
导入新课
刻度尺
三角尺
量角器
圆规
导入新课
基本作图
在几何里,把限定只用圆规和没有刻度的直尺来作几何图形的方法称为尺规作图.最基本、最常用的尺规作图,通常称基本作图.
5种基本作图:(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作已知角的平分线;
(4)经过一已知点作已知直线的垂线;
(5)作已知线段的垂直平分线.
一些复杂的尺规作图都是由基本作图组成的.
讲授新课
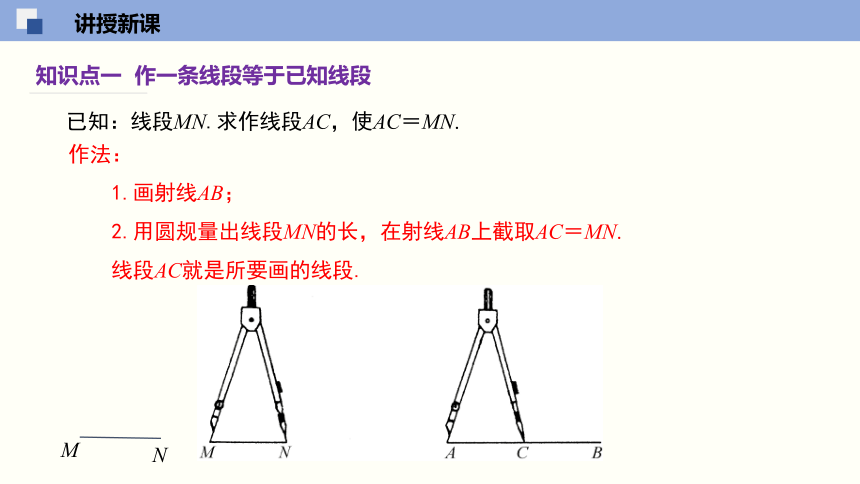
知识点一 作一条线段等于已知线段
已知:线段MN.求作线段AC,使AC=MN.
作法:
1.画射线AB;
2.用圆规量出线段MN的长,在射线AB上截取AC=MN.
线段AC就是所要画的线段.
M
N
讲授新课
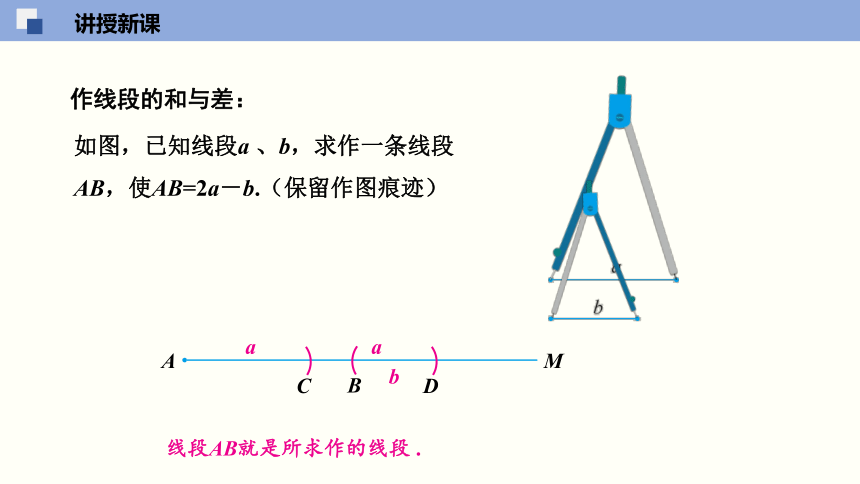
作线段的和与差:
如图,已知线段a 、b,求作一条线段AB,使AB=2a-b.(保留作图痕迹)
A
M
C
a
D
a
B
b
线段AB就是所求作的线段 .
讲授新课
作线段的和与差的方法:先画一条射线,然后在这条射线上顺次截取相应的线段,求和时顺次截取叠加,求差时从所画的线段中截去.
讲授新课
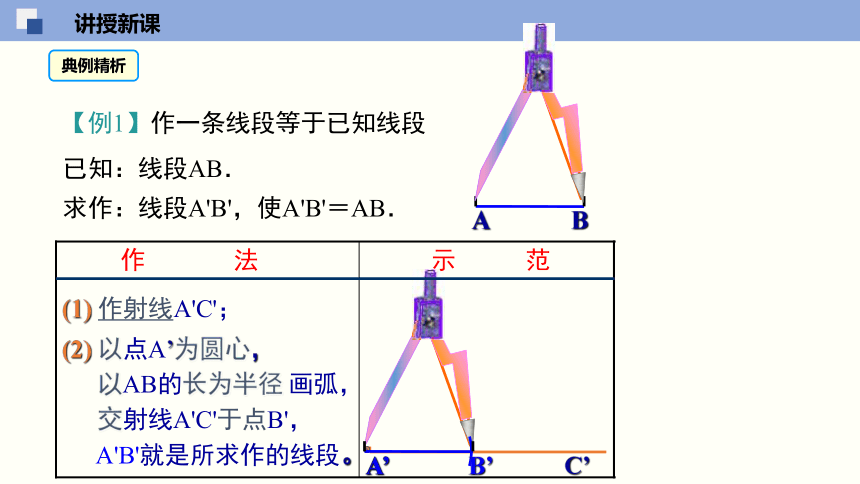
已知:线段AB.
求作:线段A'B',使A'B'=AB.
A
B
(1) 作射线A'C';
A’ C’
(2) 以点A’为圆心,
以AB的长为半径
画弧,
交射线A'C'于点B',
B’
A’
A'B'就是所求作的线段。
示 范
作 法
【例1】作一条线段等于已知线段
典例精析
讲授新课
1、已知线段a,b画一条线段c,使它的长度等于两条已知线段的长度的和.
a
b
C
b
A
D
画法:
1.画射线AD
2.用圆规在射线AD上截取AB=a
3.用圆规在射线BD上截取BC=b
线段AC就是所求的线段
a
B
练一练
讲授新课
知识点二 作一个角等于已知角
如图,已知:∠AOB .
求作:∠A′O′B′,使∠AOB=∠A′O′B′ .
还记得如何作吗?试一试.
A
O
B
讲授新课
A
O
B
O′
A′
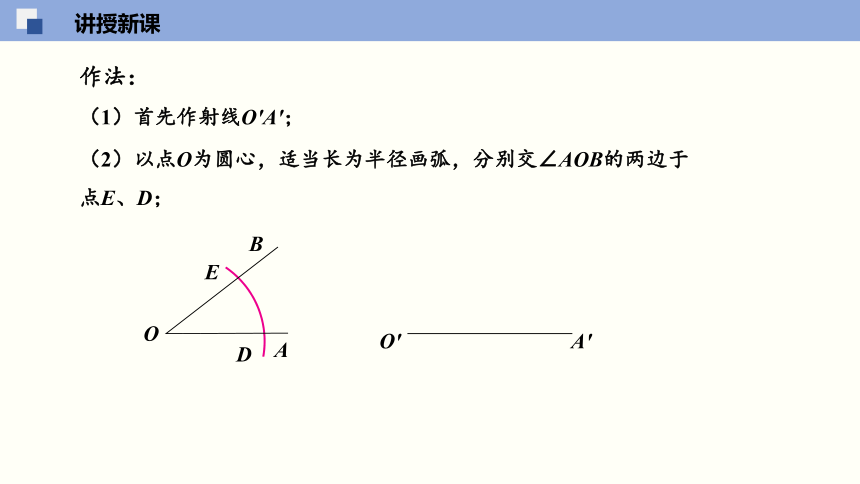
(1)首先作射线O′A′;
作法:
(2)以点O为圆心,适当长为半径画弧,分别交∠AOB的两边于点E、D;
D
E
讲授新课
A
O
B
O′
A′
(3)以点O′为圆心、OD的长为半径画弧﹐交O′A′于点N ;
作法:
(4)以点N为圆心、DE的长为半径画弧﹐交前一条弧于点M ;
N
M
(5)过点M作射线O′B′,则∠A′O′B′就是所求作的角.
B′
D
E
讲授新课
作角的和与差:
如图,已知∠1和∠2.
求作:∠AOB,使∠AOB=∠1+∠2.
讲授新课
作角的和与差:
分析:先作一个角等于∠1 ,再以∠1一条边作一个角等于∠2.
讲授新课
①在一个角的外部以这个角的一边为边作另外一个角,则两个角的另一边组成的角就是这两个角的和.
②在较大的角的内部以较大角的一边为边作较小的角﹐则两个角的另一边组成的角就是这两个角的差.
讲授新课
典例精析
已知: 如图,∠AOB.
求作: ∠A'O'B' 使∠A'O'B' =∠AOB.
B
O
A
讲授新课
B
O
A
O’
A’
(2)以点O为圆心,
任意长为半径
交OA于点C,
(3)以点O'为圆心,
画弧,
C
D
同样(OC)长为半径
画弧,
C’
(4)以点C'为圆心,
CD长为半径
画弧,
D’
(5)过点D'作射线O'B'.
B’
A’
O’
B’
∠A'O'B'就是所求的角.
作 法 示 范
(1)作射线O'A';
交OB于点D;
交O'A'于点C';
交前面的弧于点D’;
讲授新课
练一练
1、已知:∠AOB.
利用尺规作: ∠A'O'B'
使∠A'O'B'=2∠AOB.
B
O
A
作法一:
C
A’
B’
∠A’O’B’为所求.
B
O
A
法二:
C
D
C’
E
B’
O’
A
∠A’O’B’为所求.
∠AOB+∠AOB
讲授新课
知识点三 作已知角的角平分线
问题:如何用尺规作∠AOB的平分线呢?
A
B
O
讲授新课
步骤:1.在射线OA和OB上,分别截取OD,OE,使OD=OE;
2.分别以D,E为圆心,适当长(大于线段DE长的一半)为半径作圆弧,在∠AOB内,两弧交于点C;
3.作射线OC.
射线OC就是所要求作的∠AOB的平分线.
A
O
B
C
D
E
讲授新课
想一想:为什么OC是角平分线呢?你能给出证明吗?
A
O
B
C
D
E
证明:连结EC,DC.
∵OD=OE,DC=EC,OC=OC,
∴△OCD≌△OCE(SSS).
∴∠AOC=∠BOC(全等三角形的对应角相等).
注意:为简化推理格式,今后只注明主要依据,省略“已知”、“等量代换”等依据.
讲授新课
A
O
B
如何将∠AOB四等分
想一想
当堂检测
1.下列尺规作图的语句错误的是( )
A.作∠AOB,使∠AOB=3∠α
B.以点O为圆心作弧
C.以点A为圆心,线段a的长为半径作弧
D.作∠ABC,使∠ABC=∠α+∠β
【解析】作弧必须有圆心和半径,缺一不可.
B
当堂检测
2. 任意画出两条线段AB和CD,再作一条线段,使它等于AB+2CD.
M
N
AB
CD
CD
H
线段MH就是所求作的线段 .
当堂检测
3.已知:线段a,c,∠α.求作:△ABC,使BC=a,AB=c,∠ABC=∠α.
作法:(1)作一条线段BC=a;
(2)以B为顶点,BC为一边,作∠DBC=∠α;
(3)在射线BD上截取线段BA=c;
(4)连接AC, △ABC就是所求作的三角形.
a
c
α
当堂检测
4. 任意画出两个角∠1和∠2,其中∠1>∠2,再作一个角,使它等于∠1-∠2.
1
2
1
2
1
2
当堂检测
5.画一个钝角∠AOB,然后以O为顶点,以OA为一边, 在角的内部画一条射线OC,使∠AOC=90°,正确的图形是( )
【解析】由题意可知,∠AOC在∠AOB的内部,且
OA为其公共边,OA与OC的夹角为90°.
D
当堂检测
6.根据图形填空.
(1)连接_____两点.
(2)延长线段______到点______,使BC=______.
(3)在______AM上截取______=______.
(4)以点O为______,以m为______画弧交OA,OB分别于C,D.
A,B
AB
AB
C
线段
AB
a
圆心
半径
当堂检测
7.如图,已知∠A,∠B,求作一个角,使它等于∠A-∠B(不用写作法,保留作图痕迹).
【解析】作∠COD=∠A,并在∠COD的内部作∠DOE=∠B,则∠COE就是所求作的角.
课堂小结
三个基本作图
注意:
①已知:根据文字语言用数学语言写出题目中的条件;
②求作:根据题目写出要求作出的图形及此图形应满足的条件;
③作法:根据作图的过程写出每一步的操作过程.
作一条线段等于已知线段
作一个角等于已知角
作已知角的平分线的理论依据是:判定三角形全等的“边边边”
谢 谢~
13.4 尺规作图
第1课时
数学(华东师大版)
八年级 上册
第13章 全等三角形
学习目标
1、了解尺规作图的定义,会用尺规:(1)作一条线段等于已知线段;(2)作一个角等于已知角;(3)作已知角的平分线;
2、应用三角形全等的知识,解释角平分线的原理;
3、会用尺规作一个三角形;培养学生动手能力,会说求作过程.
导入新课
刻度尺
三角尺
量角器
圆规
导入新课
基本作图
在几何里,把限定只用圆规和没有刻度的直尺来作几何图形的方法称为尺规作图.最基本、最常用的尺规作图,通常称基本作图.
5种基本作图:(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作已知角的平分线;
(4)经过一已知点作已知直线的垂线;
(5)作已知线段的垂直平分线.
一些复杂的尺规作图都是由基本作图组成的.
讲授新课
知识点一 作一条线段等于已知线段
已知:线段MN.求作线段AC,使AC=MN.
作法:
1.画射线AB;
2.用圆规量出线段MN的长,在射线AB上截取AC=MN.
线段AC就是所要画的线段.
M
N
讲授新课
作线段的和与差:
如图,已知线段a 、b,求作一条线段AB,使AB=2a-b.(保留作图痕迹)
A
M
C
a
D
a
B
b
线段AB就是所求作的线段 .
讲授新课
作线段的和与差的方法:先画一条射线,然后在这条射线上顺次截取相应的线段,求和时顺次截取叠加,求差时从所画的线段中截去.
讲授新课
已知:线段AB.
求作:线段A'B',使A'B'=AB.
A
B
(1) 作射线A'C';
A’ C’
(2) 以点A’为圆心,
以AB的长为半径
画弧,
交射线A'C'于点B',
B’
A’
A'B'就是所求作的线段。
示 范
作 法
【例1】作一条线段等于已知线段
典例精析
讲授新课
1、已知线段a,b画一条线段c,使它的长度等于两条已知线段的长度的和.
a
b
C
b
A
D
画法:
1.画射线AD
2.用圆规在射线AD上截取AB=a
3.用圆规在射线BD上截取BC=b
线段AC就是所求的线段
a
B
练一练
讲授新课
知识点二 作一个角等于已知角
如图,已知:∠AOB .
求作:∠A′O′B′,使∠AOB=∠A′O′B′ .
还记得如何作吗?试一试.
A
O
B
讲授新课
A
O
B
O′
A′
(1)首先作射线O′A′;
作法:
(2)以点O为圆心,适当长为半径画弧,分别交∠AOB的两边于点E、D;
D
E
讲授新课
A
O
B
O′
A′
(3)以点O′为圆心、OD的长为半径画弧﹐交O′A′于点N ;
作法:
(4)以点N为圆心、DE的长为半径画弧﹐交前一条弧于点M ;
N
M
(5)过点M作射线O′B′,则∠A′O′B′就是所求作的角.
B′
D
E
讲授新课
作角的和与差:
如图,已知∠1和∠2.
求作:∠AOB,使∠AOB=∠1+∠2.
讲授新课
作角的和与差:
分析:先作一个角等于∠1 ,再以∠1一条边作一个角等于∠2.
讲授新课
①在一个角的外部以这个角的一边为边作另外一个角,则两个角的另一边组成的角就是这两个角的和.
②在较大的角的内部以较大角的一边为边作较小的角﹐则两个角的另一边组成的角就是这两个角的差.
讲授新课
典例精析
已知: 如图,∠AOB.
求作: ∠A'O'B' 使∠A'O'B' =∠AOB.
B
O
A
讲授新课
B
O
A
O’
A’
(2)以点O为圆心,
任意长为半径
交OA于点C,
(3)以点O'为圆心,
画弧,
C
D
同样(OC)长为半径
画弧,
C’
(4)以点C'为圆心,
CD长为半径
画弧,
D’
(5)过点D'作射线O'B'.
B’
A’
O’
B’
∠A'O'B'就是所求的角.
作 法 示 范
(1)作射线O'A';
交OB于点D;
交O'A'于点C';
交前面的弧于点D’;
讲授新课
练一练
1、已知:∠AOB.
利用尺规作: ∠A'O'B'
使∠A'O'B'=2∠AOB.
B
O
A
作法一:
C
A’
B’
∠A’O’B’为所求.
B
O
A
法二:
C
D
C’
E
B’
O’
A
∠A’O’B’为所求.
∠AOB+∠AOB
讲授新课
知识点三 作已知角的角平分线
问题:如何用尺规作∠AOB的平分线呢?
A
B
O
讲授新课
步骤:1.在射线OA和OB上,分别截取OD,OE,使OD=OE;
2.分别以D,E为圆心,适当长(大于线段DE长的一半)为半径作圆弧,在∠AOB内,两弧交于点C;
3.作射线OC.
射线OC就是所要求作的∠AOB的平分线.
A
O
B
C
D
E
讲授新课
想一想:为什么OC是角平分线呢?你能给出证明吗?
A
O
B
C
D
E
证明:连结EC,DC.
∵OD=OE,DC=EC,OC=OC,
∴△OCD≌△OCE(SSS).
∴∠AOC=∠BOC(全等三角形的对应角相等).
注意:为简化推理格式,今后只注明主要依据,省略“已知”、“等量代换”等依据.
讲授新课
A
O
B
如何将∠AOB四等分
想一想
当堂检测
1.下列尺规作图的语句错误的是( )
A.作∠AOB,使∠AOB=3∠α
B.以点O为圆心作弧
C.以点A为圆心,线段a的长为半径作弧
D.作∠ABC,使∠ABC=∠α+∠β
【解析】作弧必须有圆心和半径,缺一不可.
B
当堂检测
2. 任意画出两条线段AB和CD,再作一条线段,使它等于AB+2CD.
M
N
AB
CD
CD
H
线段MH就是所求作的线段 .
当堂检测
3.已知:线段a,c,∠α.求作:△ABC,使BC=a,AB=c,∠ABC=∠α.
作法:(1)作一条线段BC=a;
(2)以B为顶点,BC为一边,作∠DBC=∠α;
(3)在射线BD上截取线段BA=c;
(4)连接AC, △ABC就是所求作的三角形.
a
c
α
当堂检测
4. 任意画出两个角∠1和∠2,其中∠1>∠2,再作一个角,使它等于∠1-∠2.
1
2
1
2
1
2
当堂检测
5.画一个钝角∠AOB,然后以O为顶点,以OA为一边, 在角的内部画一条射线OC,使∠AOC=90°,正确的图形是( )
【解析】由题意可知,∠AOC在∠AOB的内部,且
OA为其公共边,OA与OC的夹角为90°.
D
当堂检测
6.根据图形填空.
(1)连接_____两点.
(2)延长线段______到点______,使BC=______.
(3)在______AM上截取______=______.
(4)以点O为______,以m为______画弧交OA,OB分别于C,D.
A,B
AB
AB
C
线段
AB
a
圆心
半径
当堂检测
7.如图,已知∠A,∠B,求作一个角,使它等于∠A-∠B(不用写作法,保留作图痕迹).
【解析】作∠COD=∠A,并在∠COD的内部作∠DOE=∠B,则∠COE就是所求作的角.
课堂小结
三个基本作图
注意:
①已知:根据文字语言用数学语言写出题目中的条件;
②求作:根据题目写出要求作出的图形及此图形应满足的条件;
③作法:根据作图的过程写出每一步的操作过程.
作一条线段等于已知线段
作一个角等于已知角
作已知角的平分线的理论依据是:判定三角形全等的“边边边”
谢 谢~
