13.3 等腰三角形(第2课时) 课件(共29张PPT)
文档属性
| 名称 | 13.3 等腰三角形(第2课时) 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 00:00:00 | ||
图片预览







文档简介
13.3 等腰三角形
第2课时 等腰三角形的判定
数学(华东师大版)
八年级 上册
第13章 全等三角形
学习目标
1、能用所学的知识证明等腰三角形的判定定理与等边三角形的判定定理;
2、能用等腰三角形性质定理与判定定理、等边三角形的性质定理与判定定理解决有关问题;
温故知新
A
B
C
等腰三角形的性质:
等腰三角形两腰相等。
等腰三角形两底角相等(等边对等角)。
等腰三角形底边上的高、中线及顶角的平分线互相重合(三线合一)。
等腰三角形是轴对称图形。
导入新课
情境引入
在△ABC中,AB=AC,倘若不留神,它的一部分被墨水涂没了,只留下一条底边BC和一个底角∠C,请问,有没有办法把原来的等腰三角形画出来?
A
B
C
A
讲授新课
知识点一 等腰三角形的判定
探究新知
对于一个三角形,怎样判定它是不是等腰三角形呢?
按定义,看它是否有两条边相等。
你还能找到其他的判定方法吗?
讲授新课
探索
我们知道,等腰三角形的两个底角相等.反过来,在一个三角形中,如果有两个角相等,那么它是等腰三角形吗?
画画看,你发现了什么?
讲授新课
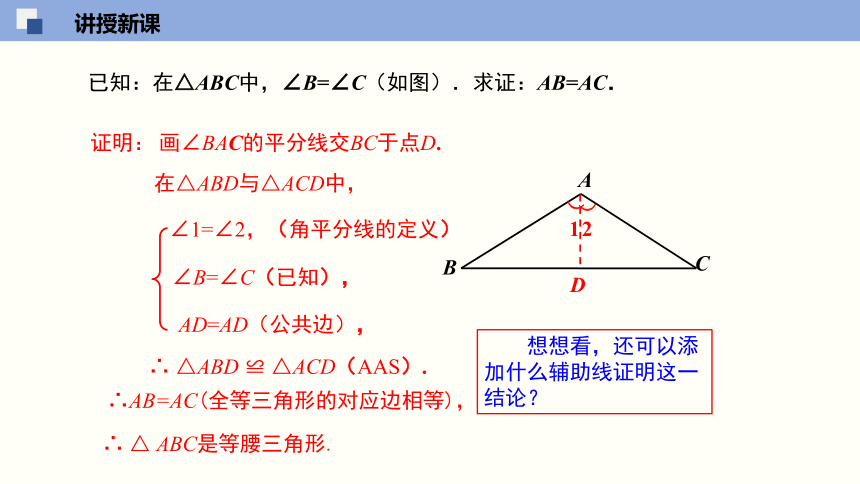
在△ABD与△ACD中,
∠1=∠2,(角平分线的定义)
∴ △ABD ≌ △ACD(AAS).
∠B=∠C(已知),
AD=AD(公共边),
∴AB=AC(全等三角形的对应边相等),
∴ △ ABC是等腰三角形.
画∠BAC的平分线交BC于点D.
证明:
C
A
B
2
1
D
(
(
已知:在△ABC中,∠B=∠C(如图).求证:AB=AC.
想想看,还可以添加什么辅助线证明这一结论?
讲授新课
等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
总结归纳
等角对等边
等边对等角
∴ AC=AB ( ).
即△ABC为等腰三角形.
∵∠B=∠C ( ),
已知
等角对等边
在△ABC中,
应用格式:
B
C
A
(
(
讲授新课
{5940675A-B579-460E-94D1-54222C63F5DA}文字语言
图形语言
符号语言
等边对等角
等角对等边
∴∠B =∠C ( 等边对等角).
A
B
C
在△ABC中,
∵AC = AB (已知),
∴AC = AB ( 等角对等边).
A
B
C
在△ABC中,
∵∠B =∠C (已知),
它们的条件与结论正好调换了过来, 这也叫互逆命题.
讲授新课
典例精析
【例1】 如图,在△ABC中,AB=AC,角平分线BD、CE相交于点O. OB与OC相等吗?请说明理由.
A
B
C
O
E
D
解:OB=OC.
理由如下:
∵AB=AC,
∴∠ABC=∠ACB (等边对等角).
∵BD、CE是角平分线,
∴∠OBC=????????∠ABC,∠OCB=????????∠ACB (角平分线定义).
∴∠OBC=∠OCB (等量代换).
∴OB=OC (等角对等边).
?
讲授新课
练一练
1、如图,在△ABC中,已知∠A=40°,∠B=70°.求证:AB=AC.
A
B
C
40°
70°
证明:∵∠A+∠B+∠C=180°
∠A=40°,∠B=70°
∴∠C=180°-∠A-∠B
=180°-40°-70°=70°
∴∠C=∠B
∴ AB=AC(等角对等边)
讲授新课
2、如图,AB//CD,∠1=∠2 . 求证:AB=AC.
A
B
C
D
2
1
证明:∵AB∥CD
∴∠B=∠2(两直线平行,同位角相等)
又∵∠1=∠2 (已知)
∴∠B=∠1 (等量代换)
∴AB=AC(等角对等边)
讲授新课
知识点二 等边三角形的判定
一个三角形满足什么条件就是等边三角形?
由等腰三角形的判定定理,可得等边三角形的两个判定定理:
1.三个角都相等的三角形是等边三角形;
2.有一个角等于60°的等腰三角形是等边三角形.
你能证明这些定理吗?
讲授新课
A
B
C
三个角都相等的三角形是等边三角形.
已知:如图,∠A= ∠ B=∠C.
求证: AB=AC=BC.
∵ ∠A= ∠ B,
∴ AC=BC.
∵ ∠ B=∠C,
∴ AB=AC.
∴AB=AC=BC.
证明:
判定1:
讲授新课
判定2:有一个角是60°的等腰三角形是等边三角形
A
B
C
已知: 若AB=AC , ∠A= 60°.
求证: AB=AC=BC.
证明:∵AB=AC , ∠A= 60 °.
∴∠B=∠C= (180。-∠A)= 60°.
∴∠A= ∠ B=∠C.
∴AB=AC=BC.
1
2
动动手
若AB=AC , ∠B= 60°,求证AB=AC=BC.
讲授新课
{5940675A-B579-460E-94D1-54222C63F5DA}
等腰三角形
边
角
特殊线
对称性
每一边上的中线、高和这一边所对的角的平分线互相重合(三条)
三个角都相等,
轴对称图形对称轴(3条)
等边三角形
轴对称图形对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合(1条)
且都是60°
两条边相等
三条边都相等
等边三角形性质归纳:
讲授新课
典例精析
【例2】 如图,已知△ABC为等边三角形,点E、F分别在边AC、BC上,且AE=CF,AF与BE相交于点D.
(1)求证:△ABE≌△CAF;
(2)求∠BDF的度数.
解:(1)证明:∵△ABC为等边三角形,
∴∠BAE=∠C=60°,AB=CA,
在△ABE和△CAF中,
????????=???????? ( 已证 ),∠????????????=∠???? ( 已证 ), ????????=???????? (已知) ,
?
∴△ABE≌△CAF (SAS).
A
B
C
D
E
F
讲授新课
解:(2)∵△ABE≌△CAF,
∴∠ABE=∠CAF.
∴∠BDF=∠ABE+∠BAF
=∠CAF+∠BAF
=∠BAC=60°.
A
B
C
D
E
F
(2)求∠BDF的度数.
讲授新课
练一练
1.如图,在等边△ABC的AC边上取中点D,BC的延长线取一点E,使CE=CD,连接BD,DE.求证:∠ABD=∠E.
A
B
C
D
E
证明: ∵△ABC为等边三角形, BD是AC边的中线,∴BD⊥AC, BD平分∠ABC,
∴∠DBE=∠ABD=????????∠ABC=30°.∵CD=CE,
∴∠CDE=∠E.∵∠ACB=60°,
∴∠CDE+∠E=60°,∴∠CDE=∠E=30°,
∴∠ABD=∠E.
?
讲授新课
2.如图, 等边△ABC中, D、E、F分别是各边上的一点, 且AD=BE=CF.
求证:△DEF是等边三角形.
证明:∵△ABC为等边三角形,且AD=BE=CF,
∴AF=BD=CE,∠A=∠B=∠C=60°,
∴△ADF≌△BED≌△CFE(SAS),
∴DF=ED=EF,
∴△DEF是等边三角形.
A
B
C
D
F
E
讲授新课
3、如图,点C为线段AB上一点,△ACM与△CBN都是等边三角形.
(1) 线段AN与线段BM是否相等?请说明理由;
B
C
A
M
N
解:(1)AN=BM.
理由:∵△ACM与△CBN都是等边三角形,
∴AC=MC,CN=CB,
∠ACM=∠BCN=60°.
∴∠ACN=∠MCB.
∴△ACN≌△MCB(SAS).
∴AN=BM.
讲授新课
(2) AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.
B
C
A
F
E
M
N
(2)△CEF是等边三角形.
证明:∵∠ACE=∠FCM=60°,
∴∠ECF=60°.
∵△ACN≌△MCB,
∴∠CAE=∠CMB.
∵AC=MC,
∴△ACE≌△MCF(ASA),
∴CE=CF.
∴△CEF是等边三角形.
想一想:本题你还能得到哪些结论?
当堂检测
1.在△ABC中, 已知∠A=50°,∠B=65°,判断△ABC是什么三角形,为什么?
△ABC是等腰三角形, 因为∠B=65°, ∠A=50°,
所以∠C=65°, ∠B =∠C=65°,
所以△ABC是等腰三角形.
2.如图,已知∠A=36°,∠DBC=36°,∠C=72°,则∠1=_____,∠2=_____,图中的等腰三角形有___________________________.
36°
72°
△ABC
△DBA
△BCD
A
B
C
D
(
(
1
2
当堂检测
B
C
D
A
E
3.如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,求∠EDA的度数.
解:
∵ △ABC是等边三角形,
∴∠CBA=60°.
∵BD是AC边上的中线,
∴∠BDA=90°, ∠DBA=30 °.
∵ BD=BE,
∴ ∠BDE=(180 °- ∠DBA) ÷2 =(180°-30°) ÷2=75°.
∴ ∠EDA=90 °- ∠BDE=90°-75°=15°.
当堂检测
4. 如图,∠A = ∠B,CE∥DA. 求证:CE = CB. 需再增加什么条件,可使△BCE成为等边三角形?
B
A
D
C
E
证明: ∵CE∥DA,
∴∠A=∠CEB .
∵∠A=∠B,
∴∠CEB=∠B,
∴CE=CB .
再增加∠B=60°,可使△BCE成为等边三角形(答案不唯一)
当堂检测
5.如图,在△ABC中,AB=AC,D是AB上一点,过D作DE⊥BC于点E,并与CA的延长线相交于点F,试判断△ADF的形状,并说明理由.
解:△ADF是等腰三角形.
理由:在△ABC中.
∵AB=AC,
∴∠B=∠C.
∵DE⊥BC,
∴∠DEB=∠DEC=90°,
∴∠BDE+∠B=90°,∠F+∠C=90°,∴∠BDE=∠F.
∵∠BDE=∠ADF,
∴∠ADF=∠F,
∴AF=AD.
∴△ADF是等腰三角形.
A
B
C
E
D
F
当堂检测
6. 如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
A
B
C
E
D
课堂小结
等腰三角形的判定
判定→等角对等边
应用→证明同一个三角形中两边相等
等边三角形→判定方法
证三个角都相等或有两个角等于60°
先证等腰三角形,再证有一个角等于60°
谢 谢~
第2课时 等腰三角形的判定
数学(华东师大版)
八年级 上册
第13章 全等三角形
学习目标
1、能用所学的知识证明等腰三角形的判定定理与等边三角形的判定定理;
2、能用等腰三角形性质定理与判定定理、等边三角形的性质定理与判定定理解决有关问题;
温故知新
A
B
C
等腰三角形的性质:
等腰三角形两腰相等。
等腰三角形两底角相等(等边对等角)。
等腰三角形底边上的高、中线及顶角的平分线互相重合(三线合一)。
等腰三角形是轴对称图形。
导入新课
情境引入
在△ABC中,AB=AC,倘若不留神,它的一部分被墨水涂没了,只留下一条底边BC和一个底角∠C,请问,有没有办法把原来的等腰三角形画出来?
A
B
C
A
讲授新课
知识点一 等腰三角形的判定
探究新知
对于一个三角形,怎样判定它是不是等腰三角形呢?
按定义,看它是否有两条边相等。
你还能找到其他的判定方法吗?
讲授新课
探索
我们知道,等腰三角形的两个底角相等.反过来,在一个三角形中,如果有两个角相等,那么它是等腰三角形吗?
画画看,你发现了什么?
讲授新课
在△ABD与△ACD中,
∠1=∠2,(角平分线的定义)
∴ △ABD ≌ △ACD(AAS).
∠B=∠C(已知),
AD=AD(公共边),
∴AB=AC(全等三角形的对应边相等),
∴ △ ABC是等腰三角形.
画∠BAC的平分线交BC于点D.
证明:
C
A
B
2
1
D
(
(
已知:在△ABC中,∠B=∠C(如图).求证:AB=AC.
想想看,还可以添加什么辅助线证明这一结论?
讲授新课
等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
总结归纳
等角对等边
等边对等角
∴ AC=AB ( ).
即△ABC为等腰三角形.
∵∠B=∠C ( ),
已知
等角对等边
在△ABC中,
应用格式:
B
C
A
(
(
讲授新课
{5940675A-B579-460E-94D1-54222C63F5DA}文字语言
图形语言
符号语言
等边对等角
等角对等边
∴∠B =∠C ( 等边对等角).
A
B
C
在△ABC中,
∵AC = AB (已知),
∴AC = AB ( 等角对等边).
A
B
C
在△ABC中,
∵∠B =∠C (已知),
它们的条件与结论正好调换了过来, 这也叫互逆命题.
讲授新课
典例精析
【例1】 如图,在△ABC中,AB=AC,角平分线BD、CE相交于点O. OB与OC相等吗?请说明理由.
A
B
C
O
E
D
解:OB=OC.
理由如下:
∵AB=AC,
∴∠ABC=∠ACB (等边对等角).
∵BD、CE是角平分线,
∴∠OBC=????????∠ABC,∠OCB=????????∠ACB (角平分线定义).
∴∠OBC=∠OCB (等量代换).
∴OB=OC (等角对等边).
?
讲授新课
练一练
1、如图,在△ABC中,已知∠A=40°,∠B=70°.求证:AB=AC.
A
B
C
40°
70°
证明:∵∠A+∠B+∠C=180°
∠A=40°,∠B=70°
∴∠C=180°-∠A-∠B
=180°-40°-70°=70°
∴∠C=∠B
∴ AB=AC(等角对等边)
讲授新课
2、如图,AB//CD,∠1=∠2 . 求证:AB=AC.
A
B
C
D
2
1
证明:∵AB∥CD
∴∠B=∠2(两直线平行,同位角相等)
又∵∠1=∠2 (已知)
∴∠B=∠1 (等量代换)
∴AB=AC(等角对等边)
讲授新课
知识点二 等边三角形的判定
一个三角形满足什么条件就是等边三角形?
由等腰三角形的判定定理,可得等边三角形的两个判定定理:
1.三个角都相等的三角形是等边三角形;
2.有一个角等于60°的等腰三角形是等边三角形.
你能证明这些定理吗?
讲授新课
A
B
C
三个角都相等的三角形是等边三角形.
已知:如图,∠A= ∠ B=∠C.
求证: AB=AC=BC.
∵ ∠A= ∠ B,
∴ AC=BC.
∵ ∠ B=∠C,
∴ AB=AC.
∴AB=AC=BC.
证明:
判定1:
讲授新课
判定2:有一个角是60°的等腰三角形是等边三角形
A
B
C
已知: 若AB=AC , ∠A= 60°.
求证: AB=AC=BC.
证明:∵AB=AC , ∠A= 60 °.
∴∠B=∠C= (180。-∠A)= 60°.
∴∠A= ∠ B=∠C.
∴AB=AC=BC.
1
2
动动手
若AB=AC , ∠B= 60°,求证AB=AC=BC.
讲授新课
{5940675A-B579-460E-94D1-54222C63F5DA}
等腰三角形
边
角
特殊线
对称性
每一边上的中线、高和这一边所对的角的平分线互相重合(三条)
三个角都相等,
轴对称图形对称轴(3条)
等边三角形
轴对称图形对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合(1条)
且都是60°
两条边相等
三条边都相等
等边三角形性质归纳:
讲授新课
典例精析
【例2】 如图,已知△ABC为等边三角形,点E、F分别在边AC、BC上,且AE=CF,AF与BE相交于点D.
(1)求证:△ABE≌△CAF;
(2)求∠BDF的度数.
解:(1)证明:∵△ABC为等边三角形,
∴∠BAE=∠C=60°,AB=CA,
在△ABE和△CAF中,
????????=???????? ( 已证 ),∠????????????=∠???? ( 已证 ), ????????=???????? (已知) ,
?
∴△ABE≌△CAF (SAS).
A
B
C
D
E
F
讲授新课
解:(2)∵△ABE≌△CAF,
∴∠ABE=∠CAF.
∴∠BDF=∠ABE+∠BAF
=∠CAF+∠BAF
=∠BAC=60°.
A
B
C
D
E
F
(2)求∠BDF的度数.
讲授新课
练一练
1.如图,在等边△ABC的AC边上取中点D,BC的延长线取一点E,使CE=CD,连接BD,DE.求证:∠ABD=∠E.
A
B
C
D
E
证明: ∵△ABC为等边三角形, BD是AC边的中线,∴BD⊥AC, BD平分∠ABC,
∴∠DBE=∠ABD=????????∠ABC=30°.∵CD=CE,
∴∠CDE=∠E.∵∠ACB=60°,
∴∠CDE+∠E=60°,∴∠CDE=∠E=30°,
∴∠ABD=∠E.
?
讲授新课
2.如图, 等边△ABC中, D、E、F分别是各边上的一点, 且AD=BE=CF.
求证:△DEF是等边三角形.
证明:∵△ABC为等边三角形,且AD=BE=CF,
∴AF=BD=CE,∠A=∠B=∠C=60°,
∴△ADF≌△BED≌△CFE(SAS),
∴DF=ED=EF,
∴△DEF是等边三角形.
A
B
C
D
F
E
讲授新课
3、如图,点C为线段AB上一点,△ACM与△CBN都是等边三角形.
(1) 线段AN与线段BM是否相等?请说明理由;
B
C
A
M
N
解:(1)AN=BM.
理由:∵△ACM与△CBN都是等边三角形,
∴AC=MC,CN=CB,
∠ACM=∠BCN=60°.
∴∠ACN=∠MCB.
∴△ACN≌△MCB(SAS).
∴AN=BM.
讲授新课
(2) AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.
B
C
A
F
E
M
N
(2)△CEF是等边三角形.
证明:∵∠ACE=∠FCM=60°,
∴∠ECF=60°.
∵△ACN≌△MCB,
∴∠CAE=∠CMB.
∵AC=MC,
∴△ACE≌△MCF(ASA),
∴CE=CF.
∴△CEF是等边三角形.
想一想:本题你还能得到哪些结论?
当堂检测
1.在△ABC中, 已知∠A=50°,∠B=65°,判断△ABC是什么三角形,为什么?
△ABC是等腰三角形, 因为∠B=65°, ∠A=50°,
所以∠C=65°, ∠B =∠C=65°,
所以△ABC是等腰三角形.
2.如图,已知∠A=36°,∠DBC=36°,∠C=72°,则∠1=_____,∠2=_____,图中的等腰三角形有___________________________.
36°
72°
△ABC
△DBA
△BCD
A
B
C
D
(
(
1
2
当堂检测
B
C
D
A
E
3.如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,求∠EDA的度数.
解:
∵ △ABC是等边三角形,
∴∠CBA=60°.
∵BD是AC边上的中线,
∴∠BDA=90°, ∠DBA=30 °.
∵ BD=BE,
∴ ∠BDE=(180 °- ∠DBA) ÷2 =(180°-30°) ÷2=75°.
∴ ∠EDA=90 °- ∠BDE=90°-75°=15°.
当堂检测
4. 如图,∠A = ∠B,CE∥DA. 求证:CE = CB. 需再增加什么条件,可使△BCE成为等边三角形?
B
A
D
C
E
证明: ∵CE∥DA,
∴∠A=∠CEB .
∵∠A=∠B,
∴∠CEB=∠B,
∴CE=CB .
再增加∠B=60°,可使△BCE成为等边三角形(答案不唯一)
当堂检测
5.如图,在△ABC中,AB=AC,D是AB上一点,过D作DE⊥BC于点E,并与CA的延长线相交于点F,试判断△ADF的形状,并说明理由.
解:△ADF是等腰三角形.
理由:在△ABC中.
∵AB=AC,
∴∠B=∠C.
∵DE⊥BC,
∴∠DEB=∠DEC=90°,
∴∠BDE+∠B=90°,∠F+∠C=90°,∴∠BDE=∠F.
∵∠BDE=∠ADF,
∴∠ADF=∠F,
∴AF=AD.
∴△ADF是等腰三角形.
A
B
C
E
D
F
当堂检测
6. 如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
A
B
C
E
D
课堂小结
等腰三角形的判定
判定→等角对等边
应用→证明同一个三角形中两边相等
等边三角形→判定方法
证三个角都相等或有两个角等于60°
先证等腰三角形,再证有一个角等于60°
谢 谢~
