13.2 三角形全等的判定(第4课时) 课件(共25张PPT)
文档属性
| 名称 | 13.2 三角形全等的判定(第4课时) 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 09:48:35 | ||
图片预览







文档简介
13.2 三角形全等的判定
第4课时 边边边
数学(华东师大版)
八年级 上册
第13章 全等三角形
学习目标
1、掌握三角形全等的“S.S.S.”判定,并能应用它判别两个三角形是否全等,以及运用该条件解决一些简单的实际问题.
2、由探索三角形全等条件的过程,体会由操作、归纳获得数学结论的过程.
温故知新
问题:目前我们已经学习了几种三角形全等的判定方法?
3种,分别是S.A.S.、A.S.A.、A.A.S.
有两边和它们的夹角对应相等的两个三角形全等
有两角和它们的夹边对应相等的两个三角形全等
有两角和其中一角的对边对应相等的两个三角形全等
S.A.S.
A.S.A.
A.A.S.
讲授新课
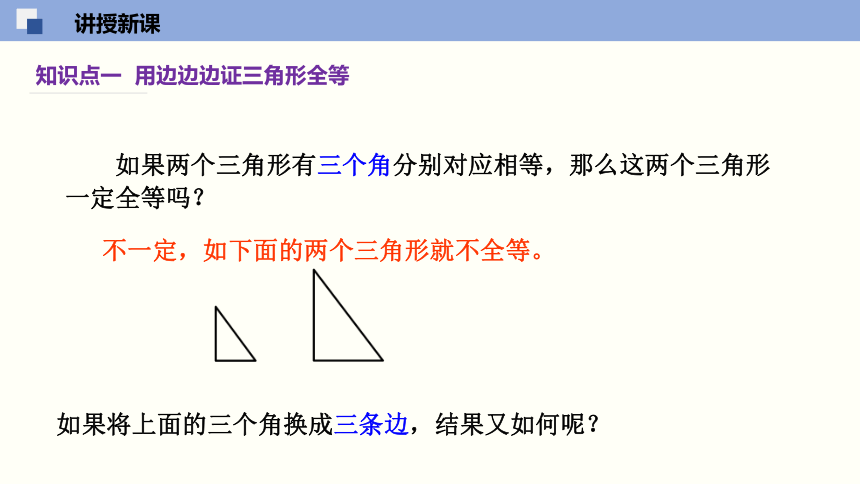
知识点一 用边边边证三角形全等
如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗?
不一定,如下面的两个三角形就不全等。
如果将上面的三个角换成三条边,结果又如何呢?
讲授新课
4 cm
a
3 cm
b
4.5 cm
c
步骤:
1.画一线段AB使它的长度等于c(4.5 cm).
2.以点A为圆心,以线段b(3cm)的长为半径画圆弧;以点B为圆心,以线段a(4cm)的长为半径画圆弧;两弧交于点C.
3.连结AC、BC.
a
b
c
A
B
C
△ABC即为所求.
把你画的三角形与其他同学画的三角形相比较,它们全等吗?
如果两个三角形有三条边分别对应相等,那么这两个三角形是否一定全等呢?
做一做
如图,已知三条线段a,b,c,试画一个三角形,使这三条线段分别为其三边.
讲授新课
文字语言:三边分别相等的两个三角形全等.
(简写为“边边边”或“S.S.S.”)
知识要点
“边边边”判定方法
A
B
C
D
E
F
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(S.S.S.).
AB=DE,
BC=EF,
CA=FD,
几何语言:
讲授新课
典例精析
【例1】如图,在四边形 ABCD 中,AD = CB,AB = CD.
求证: ∠B = ∠D.
证明:在△ABC 和△CDA 中,
∵CB = AD ,AB = CD (已知),
AC = CA (公共边),
∴△ABC≌△CDA (S.S.S.).
∴∠B = ∠D (全等三角形的对应角相等).
讲授新课
【例2】 已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.
A
B
C
D
证明:
在△ACB 和 △ADB中
AC = A D ,
BC = BD,
A B = A B (公共边),
∴△ACB≌△ADB(S.S.S.).
连结AB.
∴∠C=∠D
(全等三角形的对应角相等).
讲授新课
练一练
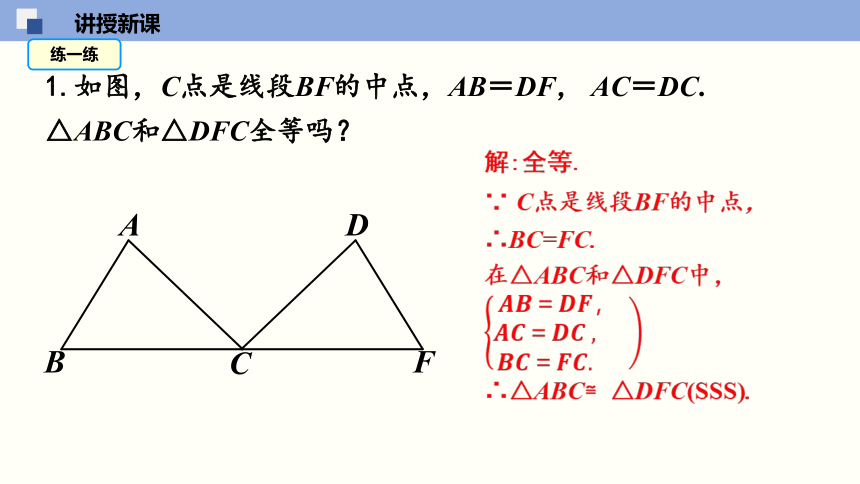
1.如图,C点是线段BF的中点,AB=DF, AC=DC.
△ABC和△DFC全等吗?
B
A
C
F
D
解:全等.
∵ C点是线段BF的中点,
∴BC=FC.
在△ABC和△DFC中,
????????=????????,????????=?????????,????????????=????????.?????
∴△ABC≌△DFC(SSS).
?
讲授新课
变式1 若将上题中右边的三角形向左平移(如图),若AB=DF,AC=DE,BE=CF.问:△ABC和△DFE全等吗?
B
A
C
E
F
D
解:全等.
∵ BE=CF ,
∴BE+EC=CF+EC.
即BC=FE .
在△ABC和△DFE中,
????????=????????,????????=?????????,????????????=????????.?????
∴△ABC≌△DFE(SSS).
?
讲授新课
变式2 若将上题中的三角形继续向左平移(如图),若AB=DC,AC=DB,问:△ABC≌△DCB 吗?
B
A
C
E
F
D
解:全等.
在△ABC和△DCB中,
????????=????????,????????=?????????,????????????=????????.?????
∴△ABC≌△DCB(SSS).
?
讲授新课
变式3 若将上题中的三角形拉开,再翻折形成下图(如图),若AB=DF, BE=CF, AC=DE, 那么∠A与∠D相等吗? 为什么?
B
A
F
D
C
F
D
E
解: ∠A与∠D相等.
∵ BE=CF ,
∴BE-CE=CF-CE.
即BC=FE .
在△ABC和△DFE中,
????????=????????,????????=?????????,????????????=????????.?????
∴△ABC≌△DFE(SSS).
∴∠A=∠D.
?
讲授新课
至此,我们已经学习了关于全等三角形的三个基本事实,这是进行演绎推理的重要依据. 它们是从静态的角度探索发现的判定方法,其本质与动态的全等三角形定义是一致的,即在这些条件下,两个三角形一定可以通过图形的基本变换 (轴对称、平移与旋转) 而相互重合.
讲授新课
概括
我们可以将前面关于全等三角形判定的探索得到的结论归纳成下表(请补充完整表格中的内容):
{5940675A-B579-460E-94D1-54222C63F5DA}对应相等的元素
两边一角
两角一边
三角
三边
两边及其夹角
两边及其中一边的对角
两角及其夹边
两角及其中一角的对边
三角形是否一定全等
一定
(S.A.S.)
一定
(A.S.A.)
不一定
(S.S.A.)
一定
(A.A.S.)
不一定
(A.A.A.)
一定
(S.S.S.)
讲授新课
三角形全等的判定思路为:
(1)已知两边:
① 找夹角(S.A.S.);
②找第三边(S.S.S.).
(2)已知一边一角:
①边为角的对边时找任一角(A.A.S.);
②边为角的邻边时,可找夹角的另一边(S.A.S.),也可以找
任一角 (A.A.S. 或 A.S.A.).
(3)已知两角:
①找夹边(A.S.A.)
②找其中一角的对边(A.A.S.)
当堂检测
1.王老师为班级中每名同学准备了长分别为a、b、c三根木条,所有同学都用三根木条,首尾顺次拼接组成三角形,这时小陈同学说:“我们所有人的三角形,形状和大小是完全一样的”小陈同学的说法依据_______.
SSS
依据:三个木条长度a,b,c,无论怎么摆放,长度不变,利用三角形全等的判定理由:SSS
当堂检测
2.如图,在△ABC中,AB=AC,EB=EC,则由“SSS”可以判定 ( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上答案都不对
A
B
C
E
D
B
由图形可知,△ABE与△ACE的三边均相等;(AE属于公共边)
当堂检测
3.如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证△ACE≌△BDF时,需添加一个条件是(????????)
B
A
C
F
D
E
A.AB=BC B.DC=BC C.AB=CD D.以上都不对
C
△ACE≌△BDF,已经知道两条边相等,要想证全等,只需要剩余的第三边相等即可;
当堂检测
4. 如图1,油纸伞是中国传统工艺品之一,起源于中国的一种纸制或布制伞.油纸伞的制作工艺十分巧妙,如图2,伞圈D沿着伞柄AP滑动时,总有伞骨BD=CD,AB=AC,从而使得伞柄AP始终平分同一平面内两条伞骨所成的∠BAC.请你说明其中的理由.
解:在△????????????和△????????????中,
????????=????????????????=????????????????=???????? ,
∴△ABD≌△ACD(SSS)
∴∠BAD=∠CAD,
即AP平分∠BAC.
?
当堂检测
5.已知:如图 ,AB=AE,AC=AD,BD=CE,求证:△ABC≌△AED.
证明:∵BD=CE,
∴BD-CD=CE-CD .
∴BC=ED .
在△ABC和△ADE中,
AC=AD(已知),
AB=AE(已知),
BC=ED(已证),
∴△ABC≌△AED(SSS).
B
A
C
E
D
当堂检测
6.已知:如图,AB=CD,AD=CB,
求证:①∠A=∠C;
② AB∥DC,AD∥ BC
A
C
D
B
①证明:连接BD .
在△ABD和△CDB中,
????????=????????(已知),????????=????????(已知),????????=????????(公共边).??
∴△ABD≌△CDB(SSS),
∴∠A=∠C.(全等三角形的对应角相等).
?
②证明:∵ △ABD≌△CDB(已证) ,
∴∠ABD=∠CDB, ∠ADB=∠CBD .
(全等三角形的对应角相等)
∴AB∥DC,AD∥BC. (内错角相等,两直线平行)
当堂检测
7.已知如图所示,点D在线段AE上,点B在线段FC上,AB=DC,AD=BC,DE=BF,求证:BE=DF .
B
A
C
F
D
E
证明:连接DB,
在△ABD和△CDB中,
∵AD=CB,AB=CD,DB=BD,
∴△ABD≌△CDB(SSS).
∴∠A=∠C.
∵AD=CB,DE=BF,
∴AD+DE=CB+BF,即AE=CF.
在△ABE和△CDF中,
AE=CF,∠A=∠C,AB=DC.
∴△ABE≌△CDF(SAS).
∴BE=DF.
当堂检测
8. 如图,点 B、E、C、F 在同一条直线上,AB = DE,AC = DF ,
BE = CF.求证:∠A = ∠D.并找出图中相互平行的线段,说明
你的理由.
证明:∵BE=CF,∴BE+CE=FC+EC,
∴BC=EF.在△ABC 和△DEF 中,
∵AB=DE,AC=DF,BC=EF,
∴△ABC≌△DEF (S.S.S.),
∴∠A =∠D .AC∥DF.
因为∠ACB=∠DFE,
所以AC∥DF.AB∥DE.
因为∠B=∠DEF,所以 AB∥DE.
课堂小结
边边边
判定定理
三边分别相等的两个三角形全等
应用
应用 S.S.S.判定三角形全等
三角形全等的判定方法的综合应用
谢 谢~
第4课时 边边边
数学(华东师大版)
八年级 上册
第13章 全等三角形
学习目标
1、掌握三角形全等的“S.S.S.”判定,并能应用它判别两个三角形是否全等,以及运用该条件解决一些简单的实际问题.
2、由探索三角形全等条件的过程,体会由操作、归纳获得数学结论的过程.
温故知新
问题:目前我们已经学习了几种三角形全等的判定方法?
3种,分别是S.A.S.、A.S.A.、A.A.S.
有两边和它们的夹角对应相等的两个三角形全等
有两角和它们的夹边对应相等的两个三角形全等
有两角和其中一角的对边对应相等的两个三角形全等
S.A.S.
A.S.A.
A.A.S.
讲授新课
知识点一 用边边边证三角形全等
如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗?
不一定,如下面的两个三角形就不全等。
如果将上面的三个角换成三条边,结果又如何呢?
讲授新课
4 cm
a
3 cm
b
4.5 cm
c
步骤:
1.画一线段AB使它的长度等于c(4.5 cm).
2.以点A为圆心,以线段b(3cm)的长为半径画圆弧;以点B为圆心,以线段a(4cm)的长为半径画圆弧;两弧交于点C.
3.连结AC、BC.
a
b
c
A
B
C
△ABC即为所求.
把你画的三角形与其他同学画的三角形相比较,它们全等吗?
如果两个三角形有三条边分别对应相等,那么这两个三角形是否一定全等呢?
做一做
如图,已知三条线段a,b,c,试画一个三角形,使这三条线段分别为其三边.
讲授新课
文字语言:三边分别相等的两个三角形全等.
(简写为“边边边”或“S.S.S.”)
知识要点
“边边边”判定方法
A
B
C
D
E
F
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(S.S.S.).
AB=DE,
BC=EF,
CA=FD,
几何语言:
讲授新课
典例精析
【例1】如图,在四边形 ABCD 中,AD = CB,AB = CD.
求证: ∠B = ∠D.
证明:在△ABC 和△CDA 中,
∵CB = AD ,AB = CD (已知),
AC = CA (公共边),
∴△ABC≌△CDA (S.S.S.).
∴∠B = ∠D (全等三角形的对应角相等).
讲授新课
【例2】 已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.
A
B
C
D
证明:
在△ACB 和 △ADB中
AC = A D ,
BC = BD,
A B = A B (公共边),
∴△ACB≌△ADB(S.S.S.).
连结AB.
∴∠C=∠D
(全等三角形的对应角相等).
讲授新课
练一练
1.如图,C点是线段BF的中点,AB=DF, AC=DC.
△ABC和△DFC全等吗?
B
A
C
F
D
解:全等.
∵ C点是线段BF的中点,
∴BC=FC.
在△ABC和△DFC中,
????????=????????,????????=?????????,????????????=????????.?????
∴△ABC≌△DFC(SSS).
?
讲授新课
变式1 若将上题中右边的三角形向左平移(如图),若AB=DF,AC=DE,BE=CF.问:△ABC和△DFE全等吗?
B
A
C
E
F
D
解:全等.
∵ BE=CF ,
∴BE+EC=CF+EC.
即BC=FE .
在△ABC和△DFE中,
????????=????????,????????=?????????,????????????=????????.?????
∴△ABC≌△DFE(SSS).
?
讲授新课
变式2 若将上题中的三角形继续向左平移(如图),若AB=DC,AC=DB,问:△ABC≌△DCB 吗?
B
A
C
E
F
D
解:全等.
在△ABC和△DCB中,
????????=????????,????????=?????????,????????????=????????.?????
∴△ABC≌△DCB(SSS).
?
讲授新课
变式3 若将上题中的三角形拉开,再翻折形成下图(如图),若AB=DF, BE=CF, AC=DE, 那么∠A与∠D相等吗? 为什么?
B
A
F
D
C
F
D
E
解: ∠A与∠D相等.
∵ BE=CF ,
∴BE-CE=CF-CE.
即BC=FE .
在△ABC和△DFE中,
????????=????????,????????=?????????,????????????=????????.?????
∴△ABC≌△DFE(SSS).
∴∠A=∠D.
?
讲授新课
至此,我们已经学习了关于全等三角形的三个基本事实,这是进行演绎推理的重要依据. 它们是从静态的角度探索发现的判定方法,其本质与动态的全等三角形定义是一致的,即在这些条件下,两个三角形一定可以通过图形的基本变换 (轴对称、平移与旋转) 而相互重合.
讲授新课
概括
我们可以将前面关于全等三角形判定的探索得到的结论归纳成下表(请补充完整表格中的内容):
{5940675A-B579-460E-94D1-54222C63F5DA}对应相等的元素
两边一角
两角一边
三角
三边
两边及其夹角
两边及其中一边的对角
两角及其夹边
两角及其中一角的对边
三角形是否一定全等
一定
(S.A.S.)
一定
(A.S.A.)
不一定
(S.S.A.)
一定
(A.A.S.)
不一定
(A.A.A.)
一定
(S.S.S.)
讲授新课
三角形全等的判定思路为:
(1)已知两边:
① 找夹角(S.A.S.);
②找第三边(S.S.S.).
(2)已知一边一角:
①边为角的对边时找任一角(A.A.S.);
②边为角的邻边时,可找夹角的另一边(S.A.S.),也可以找
任一角 (A.A.S. 或 A.S.A.).
(3)已知两角:
①找夹边(A.S.A.)
②找其中一角的对边(A.A.S.)
当堂检测
1.王老师为班级中每名同学准备了长分别为a、b、c三根木条,所有同学都用三根木条,首尾顺次拼接组成三角形,这时小陈同学说:“我们所有人的三角形,形状和大小是完全一样的”小陈同学的说法依据_______.
SSS
依据:三个木条长度a,b,c,无论怎么摆放,长度不变,利用三角形全等的判定理由:SSS
当堂检测
2.如图,在△ABC中,AB=AC,EB=EC,则由“SSS”可以判定 ( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上答案都不对
A
B
C
E
D
B
由图形可知,△ABE与△ACE的三边均相等;(AE属于公共边)
当堂检测
3.如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证△ACE≌△BDF时,需添加一个条件是(????????)
B
A
C
F
D
E
A.AB=BC B.DC=BC C.AB=CD D.以上都不对
C
△ACE≌△BDF,已经知道两条边相等,要想证全等,只需要剩余的第三边相等即可;
当堂检测
4. 如图1,油纸伞是中国传统工艺品之一,起源于中国的一种纸制或布制伞.油纸伞的制作工艺十分巧妙,如图2,伞圈D沿着伞柄AP滑动时,总有伞骨BD=CD,AB=AC,从而使得伞柄AP始终平分同一平面内两条伞骨所成的∠BAC.请你说明其中的理由.
解:在△????????????和△????????????中,
????????=????????????????=????????????????=???????? ,
∴△ABD≌△ACD(SSS)
∴∠BAD=∠CAD,
即AP平分∠BAC.
?
当堂检测
5.已知:如图 ,AB=AE,AC=AD,BD=CE,求证:△ABC≌△AED.
证明:∵BD=CE,
∴BD-CD=CE-CD .
∴BC=ED .
在△ABC和△ADE中,
AC=AD(已知),
AB=AE(已知),
BC=ED(已证),
∴△ABC≌△AED(SSS).
B
A
C
E
D
当堂检测
6.已知:如图,AB=CD,AD=CB,
求证:①∠A=∠C;
② AB∥DC,AD∥ BC
A
C
D
B
①证明:连接BD .
在△ABD和△CDB中,
????????=????????(已知),????????=????????(已知),????????=????????(公共边).??
∴△ABD≌△CDB(SSS),
∴∠A=∠C.(全等三角形的对应角相等).
?
②证明:∵ △ABD≌△CDB(已证) ,
∴∠ABD=∠CDB, ∠ADB=∠CBD .
(全等三角形的对应角相等)
∴AB∥DC,AD∥BC. (内错角相等,两直线平行)
当堂检测
7.已知如图所示,点D在线段AE上,点B在线段FC上,AB=DC,AD=BC,DE=BF,求证:BE=DF .
B
A
C
F
D
E
证明:连接DB,
在△ABD和△CDB中,
∵AD=CB,AB=CD,DB=BD,
∴△ABD≌△CDB(SSS).
∴∠A=∠C.
∵AD=CB,DE=BF,
∴AD+DE=CB+BF,即AE=CF.
在△ABE和△CDF中,
AE=CF,∠A=∠C,AB=DC.
∴△ABE≌△CDF(SAS).
∴BE=DF.
当堂检测
8. 如图,点 B、E、C、F 在同一条直线上,AB = DE,AC = DF ,
BE = CF.求证:∠A = ∠D.并找出图中相互平行的线段,说明
你的理由.
证明:∵BE=CF,∴BE+CE=FC+EC,
∴BC=EF.在△ABC 和△DEF 中,
∵AB=DE,AC=DF,BC=EF,
∴△ABC≌△DEF (S.S.S.),
∴∠A =∠D .AC∥DF.
因为∠ACB=∠DFE,
所以AC∥DF.AB∥DE.
因为∠B=∠DEF,所以 AB∥DE.
课堂小结
边边边
判定定理
三边分别相等的两个三角形全等
应用
应用 S.S.S.判定三角形全等
三角形全等的判定方法的综合应用
谢 谢~
