13.3 等腰三角形(第1课时) 课件(共32张PPT)
文档属性
| 名称 | 13.3 等腰三角形(第1课时) 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 09:50:27 | ||
图片预览











文档简介
13.3 等腰三角形
第1课时 等腰三角形的性质
数学(华东师大版)
八年级 上册
第13章 全等三角形
学习目标
1、理解并掌握等腰三角形的性质;
2、经历等腰三角形的探究过程,能初步运用等腰三角形的性质解决有关问题;
温故知新
有两条边相等的三角形叫做等腰三角形.
1.具备什么条件的三角形是等腰三角形?
2.等腰三角形的有关概念
A
B
C
相等的两条边叫做腰,
另一条边叫做底边,
底边与腰的夹角叫做底角.
两腰所夹的角叫做顶角,
腰
腰
底边
顶角
底角
边:
角:
导入新课
法国巴黎的卢浮宫
城市大桥建筑
图片欣赏
讲授新课
知识点一 等腰三角形的性质
剪一张等腰三角形的半透明纸片,每人所剪的等腰三角形的大小和形状可以不一样,如图,把纸片对折,让两腰AB、AC重叠在一起,折痕为AD.你能发现什么现象吗?
做一做
D
A
B
C
讲授新课
1.等腰三角形是轴对称图形.
我们可以得出结论:
A
C
B
D
折痕AD所在直线是等腰三角形的对称轴.
你还有新的发现吗?
∠B,∠C 是等腰三角形的 .
底角
∠B =∠C
所以我们可以描述为:
等腰三角形的两个底角相等.
2.
探究归纳
讲授新课
A
B
C
D
等腰三角形的性质:
等腰三角形的两底角相等.
(简写成“等边对等角”)
你还有什么方法可以证明“等边对等角”呢?
讲授新课
A
B
C
已知:如图,在△ABC中,AB=AC.
求证:∠B =∠C
证明:画∠BAC的平分线AD.
D
1
2
在△ABD和△ACD中,
∵AB=AC(已知)
∠1=∠2(角平分线的定义)
AD=AD(公共边)
∴ △ABD≌△ACD(S.A.S)
∴∠B=∠C(全等三角形的对应角相等)
讲授新课
从这里你还可以得到什么结论?
A
B
C
D
1
2
AD既是底边上的中线,又是顶角的平分线和底边上的高。
讲授新课
A
B
C
D
1
2
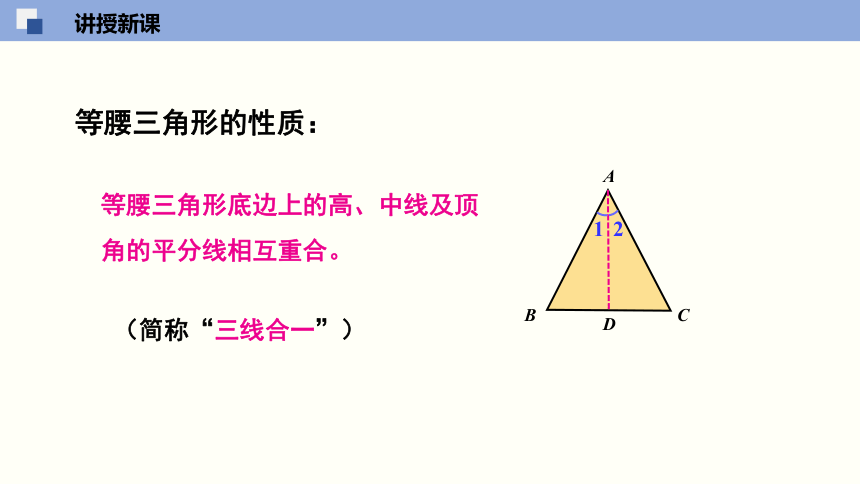
等腰三角形底边上的高、中线及顶角的平分线相互重合。
等腰三角形的性质:
(简称“三线合一”)
讲授新课
{5940675A-B579-460E-94D1-54222C63F5DA}文字语言
图形语言
符号语言
等边对等角
底边上的高、中线及顶角平分线重合
A
B
C
A
B
C
D
在△ABC中,
∵AC = AB (已知),
∴∠B =∠C ( 等边对等角).
在△ABC中,AB=AC.
(1)∵∠BAD=∠CAD,∴BD=CD,AD⊥BC;
(2)∵AD⊥BC,∴BD=CD,∠BAD=∠CAD;
(3)∵BD=CD,∴∠BAD=∠CAD,AD⊥BC.
知识归纳
讲授新课
典例精析
例1 已知:如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,
求证: ∠ADB=∠BAC.
A
B
C
D
1
2
?
?
证明:∵AB=AC,AD=BD,
∴∠B=∠C,∠B=∠1(等边对等角)
∴∠C=∠1.
∵∠ADB是△ADC的外角,
∴∠ADB=∠C+∠2.
∴∠ADB=∠1+∠2=∠BAC.
讲授新课
例2 已知:如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.
求证:DE=DF.
D
A
B
C
F
E
证明:
∵AB=AC,
∴ ∠B= ∠C (等边对等角).
∵D是BC的中点,
∴ DB=DC .
∵DE⊥AB,DF⊥AC,
∴ ∠DEB=∠DFC=90°.
在△DBE和△DCF中,
∠????= ∠???? , ∠????????????=∠????????????=????????°,????????=????????,
?
∴ △DBE ≌ △DCF(AAS).
∴ DE=DF .
讲授新课
练一练
1. 如图,在△ABC中,AB=AC,
(1)如果∠B=70°,那么∠C=____,∠A=____.
A
B
C
D
70°
40°
(2)如果∠A=70°,那么∠B=____,∠C= ___.
(3)如果有一个角等于120°,
那么∠A= ____ ,∠B=___ ,∠C =___ .
(4)如果有一个角等于50°,那么另两个角等于多少度?
55°
55°
120°
30°
30°
解:若∠A=50°,则∠B=∠C=65°;
若∠B=∠C=50°,则∠A=80°.
已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论.
讲授新课
2. 如图,在△ABC中,点D在BC上,AD=BD,AB=AC=CD.
找出图中相等的角并说明理由.
解:∠BAD=∠B=∠C;∠BAC=∠ADB;∠ADC=∠DAC.
∵AD=BD,
∴∠BAD=∠B.
∵AB=AC,
∴∠C=∠B.
∴∠BAD=∠B=∠C
A
B
C
D
∵DC=AC,
∴∠DAC=∠ADC.
∵∠ADB=∠C+∠DAC,
∠BAC=∠BAD+∠DAC,
∴∠ADB=∠BAC.
讲授新课
3.如图的房屋人字梁架中,AB=AC ,BD=DC, ∠BAC=110°,
(1) 求∠B、∠C、∠1、∠2的度数;
(2) 求证:AD⊥BC .
(2) 证明:∵AB=AC,BD=DC(已知)
∴ AD⊥BC(三线合一)
1
2
解: (1) ∵AB=AC,BD=DC(已知)
∴∠1=∠2= ????????∠BAC(三线合一)
∵∠BAC=110°(已知)
∴∠ 1=∠2=55°(等式性质)
?
讲授新课
知识点二 等边三角形的性质
因为等边三角形是特殊的等腰三角形,由等腰三角形等边对等角的性质得到,∠B= ∠ C,
同理可得 ∠A=∠B
所以 ∠A=∠B=∠C,
又由 ∠A+∠B+∠C=180°,
从而推出 ∠A=∠B=∠C=60°.
也就是说:等边三角形的各个角都相等,并且每一个角都等于60°.
三条边都相等的三角形是等边三角形,它也是轴对称图形,那么等边三角形的每个角的度数是多少呢?它有几条对称轴?
A
C
B
等边三角形的三条边都相等,三个角都相等,也称为正三角形.
三条对称轴
讲授新课
A
B
C
等边三角形的各个角都相等,并且每一个角都等于60°.
等边三角形的性质:
正三角形
讲授新课
典例精析
A
B
C
D
例3 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
(1)找出图中所有相等的角;
(2)指出图中有几个等腰三角形?
∠A=∠ABD,
∠C=∠BDC=∠ABC;
△ABC,
△ABD,
△BCD;
讲授新课
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
(3)观察∠BDC与∠A,∠ABD的关系,∠ABC、∠C呢?
∠BDC= ∠A+ ∠ABD=2 ∠A=2 ∠ABD,
∠ABC= ∠BDC=2 ∠A,
∠C= ∠BDC=2 ∠A;
(4)设∠A=x,请把△ ABC的内角和用含x的式子表示出来.
∵ ∠A+ ∠ABC+ ∠ C=180 °,
∴x+2x+2x=180 °.
讲授新课
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180 ° ,
解得x=36 ° .
在△ABC中,∠A=36°,∠ABC=∠C=72°.
x
⌒
2x
⌒
2x
⌒
⌒
2x
当堂检测
D
1.等腰三角形的对称轴是 ( )
A.底边上的中线 B.顶角的平分线
C.底边上的高 D.底边的垂直平分线
注:对称轴要回答是直线,而ABC三个选项是线段或射线,不符合要求
当堂检测
2.如图,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是 ( )
A. ∠B=∠C B. AD⊥BC
C. AD平分∠BAC D. AB=2BD
A
B
C
D
D
根据等腰三角形的性质即可证明ABC,D无法说明;
当堂检测
3.(1)等腰三角形一个底角为75°,它的另外两个角为____ ________;
(2)等腰三角形一个角为36°,它的另外两个角为____________________;
(3)等腰三角形一个角为120°,它的另外两个角为_ ___ _______ __.
75°, 30°
72°,72°或36°,108°
30°,30°
当堂检测
4. 在△ABC中, AB=AC,AB的垂直平分线与AC所在的直线相交得的锐角为50°,则底角的大小为___________.
70°或20°
A
B
C
A
B
C
注意:当题目未给定三角形的形状时,一般需分锐角三角形和钝角三角形两种情况进行讨论.
当堂检测
5. 如图,点E在BC上,AE// DC, AB = AE. 求证:∠B = ∠C.
A
D
C
E
B
证明:∵AE//DC,
∴∠C=∠AEB.
又∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠C.
当堂检测
6. 如图,在△ABC中,AB = AC,BD ⊥AC,CE ⊥AB,垂足分别为点D、E. 求证:BD=CE.
证明:∵AB=AC,
∴∠EBC=∠DCB,
∵BD⊥AC,CE⊥AB,
∴∠BEC=∠CDB=90°.
在△BEC和△CDB中,
∠BEC=∠CDB,∠EBC=∠DCB,BC=CB
∴△BEC≌△CDB(A.A.S.),
∴BD=CE .
当堂检测
7.如图,在△ABC中,点D在BC上,AD=BD,AB=AC=CD.
求∠BAC的度数.
解:设∠B=x°.
∵AD=BD,
∴∠BAD=∠B=x°.
∴∠ADC=∠BAD+∠B=(2x)°.
∵DC=AC,
∴∠DAC=∠ADC=(2x)°.
∵AB=AC,
∴∠C=∠B=x°.
∵∠C+∠DAC+∠ADC=180°,
∴x+2x+2x=180.
∴x=36,即∠B=36°.
∴∠BAC=180°-36°-36°=108°
A
B
C
D
当堂检测
8. 已知点D、E在△ABC的边BC上,AB=AC.
(1)如图①,若AD=AE,求证:BD=CE;
A
C
B
E
D
图①
G
(1)证明:如图①,过A作AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE.
当堂检测
A
F
C
B
E
D
图②
(2)证明:∵F为DE的中点,
∴DF=EF.
∵BD=CE,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,
∴AF⊥BC.
(2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC.
课堂小结
等腰三角形的性质
底与腰不相等
定义
等边对等角→证明角相等
三线合一
底与腰相等→等边三角形
定义
等腰三角形的所有性质
特有性质:三边相等;三个角都等于60°
谢 谢~
第1课时 等腰三角形的性质
数学(华东师大版)
八年级 上册
第13章 全等三角形
学习目标
1、理解并掌握等腰三角形的性质;
2、经历等腰三角形的探究过程,能初步运用等腰三角形的性质解决有关问题;
温故知新
有两条边相等的三角形叫做等腰三角形.
1.具备什么条件的三角形是等腰三角形?
2.等腰三角形的有关概念
A
B
C
相等的两条边叫做腰,
另一条边叫做底边,
底边与腰的夹角叫做底角.
两腰所夹的角叫做顶角,
腰
腰
底边
顶角
底角
边:
角:
导入新课
法国巴黎的卢浮宫
城市大桥建筑
图片欣赏
讲授新课
知识点一 等腰三角形的性质
剪一张等腰三角形的半透明纸片,每人所剪的等腰三角形的大小和形状可以不一样,如图,把纸片对折,让两腰AB、AC重叠在一起,折痕为AD.你能发现什么现象吗?
做一做
D
A
B
C
讲授新课
1.等腰三角形是轴对称图形.
我们可以得出结论:
A
C
B
D
折痕AD所在直线是等腰三角形的对称轴.
你还有新的发现吗?
∠B,∠C 是等腰三角形的 .
底角
∠B =∠C
所以我们可以描述为:
等腰三角形的两个底角相等.
2.
探究归纳
讲授新课
A
B
C
D
等腰三角形的性质:
等腰三角形的两底角相等.
(简写成“等边对等角”)
你还有什么方法可以证明“等边对等角”呢?
讲授新课
A
B
C
已知:如图,在△ABC中,AB=AC.
求证:∠B =∠C
证明:画∠BAC的平分线AD.
D
1
2
在△ABD和△ACD中,
∵AB=AC(已知)
∠1=∠2(角平分线的定义)
AD=AD(公共边)
∴ △ABD≌△ACD(S.A.S)
∴∠B=∠C(全等三角形的对应角相等)
讲授新课
从这里你还可以得到什么结论?
A
B
C
D
1
2
AD既是底边上的中线,又是顶角的平分线和底边上的高。
讲授新课
A
B
C
D
1
2
等腰三角形底边上的高、中线及顶角的平分线相互重合。
等腰三角形的性质:
(简称“三线合一”)
讲授新课
{5940675A-B579-460E-94D1-54222C63F5DA}文字语言
图形语言
符号语言
等边对等角
底边上的高、中线及顶角平分线重合
A
B
C
A
B
C
D
在△ABC中,
∵AC = AB (已知),
∴∠B =∠C ( 等边对等角).
在△ABC中,AB=AC.
(1)∵∠BAD=∠CAD,∴BD=CD,AD⊥BC;
(2)∵AD⊥BC,∴BD=CD,∠BAD=∠CAD;
(3)∵BD=CD,∴∠BAD=∠CAD,AD⊥BC.
知识归纳
讲授新课
典例精析
例1 已知:如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,
求证: ∠ADB=∠BAC.
A
B
C
D
1
2
?
?
证明:∵AB=AC,AD=BD,
∴∠B=∠C,∠B=∠1(等边对等角)
∴∠C=∠1.
∵∠ADB是△ADC的外角,
∴∠ADB=∠C+∠2.
∴∠ADB=∠1+∠2=∠BAC.
讲授新课
例2 已知:如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.
求证:DE=DF.
D
A
B
C
F
E
证明:
∵AB=AC,
∴ ∠B= ∠C (等边对等角).
∵D是BC的中点,
∴ DB=DC .
∵DE⊥AB,DF⊥AC,
∴ ∠DEB=∠DFC=90°.
在△DBE和△DCF中,
∠????= ∠???? , ∠????????????=∠????????????=????????°,????????=????????,
?
∴ △DBE ≌ △DCF(AAS).
∴ DE=DF .
讲授新课
练一练
1. 如图,在△ABC中,AB=AC,
(1)如果∠B=70°,那么∠C=____,∠A=____.
A
B
C
D
70°
40°
(2)如果∠A=70°,那么∠B=____,∠C= ___.
(3)如果有一个角等于120°,
那么∠A= ____ ,∠B=___ ,∠C =___ .
(4)如果有一个角等于50°,那么另两个角等于多少度?
55°
55°
120°
30°
30°
解:若∠A=50°,则∠B=∠C=65°;
若∠B=∠C=50°,则∠A=80°.
已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论.
讲授新课
2. 如图,在△ABC中,点D在BC上,AD=BD,AB=AC=CD.
找出图中相等的角并说明理由.
解:∠BAD=∠B=∠C;∠BAC=∠ADB;∠ADC=∠DAC.
∵AD=BD,
∴∠BAD=∠B.
∵AB=AC,
∴∠C=∠B.
∴∠BAD=∠B=∠C
A
B
C
D
∵DC=AC,
∴∠DAC=∠ADC.
∵∠ADB=∠C+∠DAC,
∠BAC=∠BAD+∠DAC,
∴∠ADB=∠BAC.
讲授新课
3.如图的房屋人字梁架中,AB=AC ,BD=DC, ∠BAC=110°,
(1) 求∠B、∠C、∠1、∠2的度数;
(2) 求证:AD⊥BC .
(2) 证明:∵AB=AC,BD=DC(已知)
∴ AD⊥BC(三线合一)
1
2
解: (1) ∵AB=AC,BD=DC(已知)
∴∠1=∠2= ????????∠BAC(三线合一)
∵∠BAC=110°(已知)
∴∠ 1=∠2=55°(等式性质)
?
讲授新课
知识点二 等边三角形的性质
因为等边三角形是特殊的等腰三角形,由等腰三角形等边对等角的性质得到,∠B= ∠ C,
同理可得 ∠A=∠B
所以 ∠A=∠B=∠C,
又由 ∠A+∠B+∠C=180°,
从而推出 ∠A=∠B=∠C=60°.
也就是说:等边三角形的各个角都相等,并且每一个角都等于60°.
三条边都相等的三角形是等边三角形,它也是轴对称图形,那么等边三角形的每个角的度数是多少呢?它有几条对称轴?
A
C
B
等边三角形的三条边都相等,三个角都相等,也称为正三角形.
三条对称轴
讲授新课
A
B
C
等边三角形的各个角都相等,并且每一个角都等于60°.
等边三角形的性质:
正三角形
讲授新课
典例精析
A
B
C
D
例3 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
(1)找出图中所有相等的角;
(2)指出图中有几个等腰三角形?
∠A=∠ABD,
∠C=∠BDC=∠ABC;
△ABC,
△ABD,
△BCD;
讲授新课
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
(3)观察∠BDC与∠A,∠ABD的关系,∠ABC、∠C呢?
∠BDC= ∠A+ ∠ABD=2 ∠A=2 ∠ABD,
∠ABC= ∠BDC=2 ∠A,
∠C= ∠BDC=2 ∠A;
(4)设∠A=x,请把△ ABC的内角和用含x的式子表示出来.
∵ ∠A+ ∠ABC+ ∠ C=180 °,
∴x+2x+2x=180 °.
讲授新课
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180 ° ,
解得x=36 ° .
在△ABC中,∠A=36°,∠ABC=∠C=72°.
x
⌒
2x
⌒
2x
⌒
⌒
2x
当堂检测
D
1.等腰三角形的对称轴是 ( )
A.底边上的中线 B.顶角的平分线
C.底边上的高 D.底边的垂直平分线
注:对称轴要回答是直线,而ABC三个选项是线段或射线,不符合要求
当堂检测
2.如图,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是 ( )
A. ∠B=∠C B. AD⊥BC
C. AD平分∠BAC D. AB=2BD
A
B
C
D
D
根据等腰三角形的性质即可证明ABC,D无法说明;
当堂检测
3.(1)等腰三角形一个底角为75°,它的另外两个角为____ ________;
(2)等腰三角形一个角为36°,它的另外两个角为____________________;
(3)等腰三角形一个角为120°,它的另外两个角为_ ___ _______ __.
75°, 30°
72°,72°或36°,108°
30°,30°
当堂检测
4. 在△ABC中, AB=AC,AB的垂直平分线与AC所在的直线相交得的锐角为50°,则底角的大小为___________.
70°或20°
A
B
C
A
B
C
注意:当题目未给定三角形的形状时,一般需分锐角三角形和钝角三角形两种情况进行讨论.
当堂检测
5. 如图,点E在BC上,AE// DC, AB = AE. 求证:∠B = ∠C.
A
D
C
E
B
证明:∵AE//DC,
∴∠C=∠AEB.
又∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠C.
当堂检测
6. 如图,在△ABC中,AB = AC,BD ⊥AC,CE ⊥AB,垂足分别为点D、E. 求证:BD=CE.
证明:∵AB=AC,
∴∠EBC=∠DCB,
∵BD⊥AC,CE⊥AB,
∴∠BEC=∠CDB=90°.
在△BEC和△CDB中,
∠BEC=∠CDB,∠EBC=∠DCB,BC=CB
∴△BEC≌△CDB(A.A.S.),
∴BD=CE .
当堂检测
7.如图,在△ABC中,点D在BC上,AD=BD,AB=AC=CD.
求∠BAC的度数.
解:设∠B=x°.
∵AD=BD,
∴∠BAD=∠B=x°.
∴∠ADC=∠BAD+∠B=(2x)°.
∵DC=AC,
∴∠DAC=∠ADC=(2x)°.
∵AB=AC,
∴∠C=∠B=x°.
∵∠C+∠DAC+∠ADC=180°,
∴x+2x+2x=180.
∴x=36,即∠B=36°.
∴∠BAC=180°-36°-36°=108°
A
B
C
D
当堂检测
8. 已知点D、E在△ABC的边BC上,AB=AC.
(1)如图①,若AD=AE,求证:BD=CE;
A
C
B
E
D
图①
G
(1)证明:如图①,过A作AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE.
当堂检测
A
F
C
B
E
D
图②
(2)证明:∵F为DE的中点,
∴DF=EF.
∵BD=CE,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,
∴AF⊥BC.
(2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC.
课堂小结
等腰三角形的性质
底与腰不相等
定义
等边对等角→证明角相等
三线合一
底与腰相等→等边三角形
定义
等腰三角形的所有性质
特有性质:三边相等;三个角都等于60°
谢 谢~
