19.5角的平分线(第2课时) 课件(共23张PPT)
文档属性
| 名称 | 19.5角的平分线(第2课时) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-24 09:49:34 | ||
图片预览







文档简介
(共23张PPT)
沪教版八年级上册
第 19 章 几何证明
19.5角的平分线(第2课时)
学习目标
1.进一步理解巩固线段的垂直平分线和角的平分线的性质定理;
2.能够应用角的平分线性质定理及其逆定理解决简单的几何问题;
3.通过探索和证明,发展推理意识和能力.
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
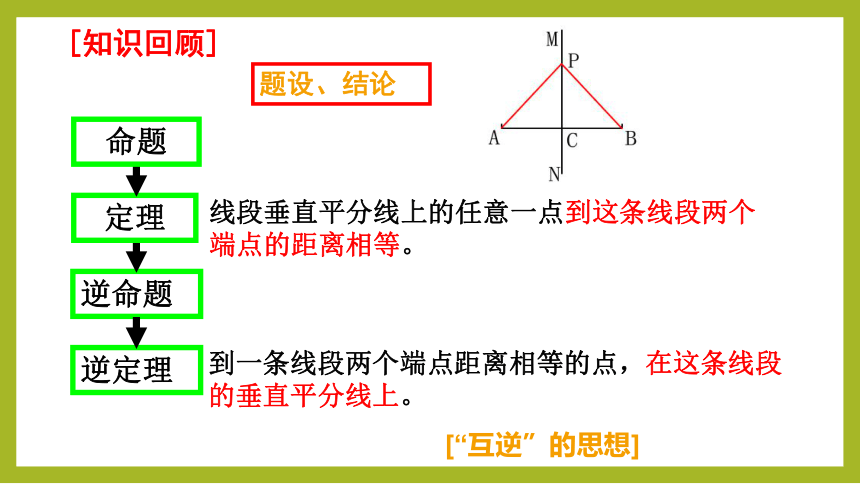
[知识回顾]
线段垂直平分线上的任意一点到这条线段两个端点的距离相等。
题设、结论
[“互逆”的思想]
逆命题
逆定理
定理
命题
逆命题
逆定理
定理
在角的平分线上的点到这个角的两边的距离相等。
在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上。
[知识回顾]
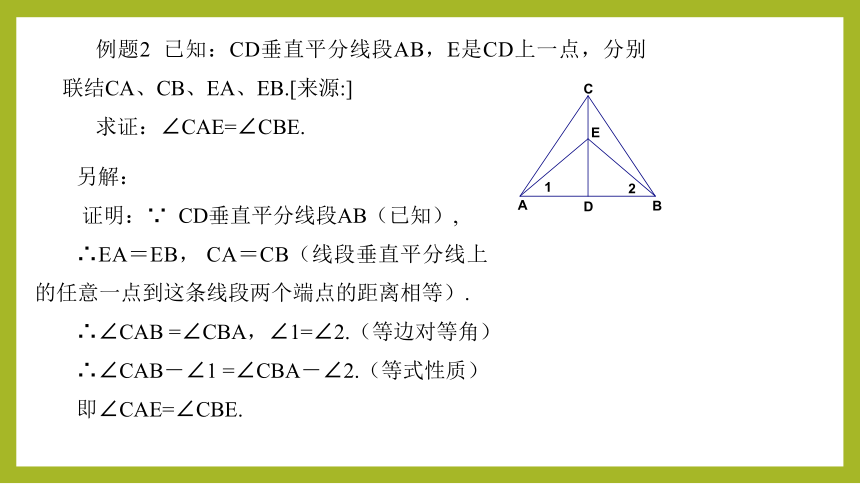
例题2 已知:CD垂直平分线段AB,E是CD上一点,分别联结CA、CB、EA、EB.[来源:]
求证:∠CAE=∠CBE.
分析:要证明∠CAE=∠CBE,可以通过△CAE≌△CBE来达到.也可以通过∠CAB-∠EAB=∠CBA-∠EBA来达到.
例题2 已知:CD垂直平分线段AB,E是CD上一点,分别联结CA、CB、EA、EB.[来源:]
求证:∠CAE=∠CBE.
证明:∵ CD垂直平分线段AB(已知),
∴EA=EB, CA=CB(线段垂直平分线上的任意
一点到这条线段两个端点的距离相等).
在△CAE与△CBE中,
(已证)
(已证)
(公共边)
∴△CAE≌△CBE(S.S.S).
∴∠CAE=∠CBE(全等三角形的对应角相等).
例题2 已知:CD垂直平分线段AB,E是CD上一点,分别联结CA、CB、EA、EB.[来源:]
求证:∠CAE=∠CBE.
另解:
证明:∵ CD垂直平分线段AB(已知),
∴EA=EB, CA=CB(线段垂直平分线上的任意一点到这条线段两个端点的距离相等).
∴∠CAB =∠CBA,∠1=∠2.(等边对等角)
∴∠CAB-∠1 =∠CBA-∠2.(等式性质)
即∠CAE=∠CBE.
例题3 已知CD⊥AB,BE⊥AC,垂足分别是
点D、E;BE、CD相交于点O,且AO平分∠BAC.
求证:OB=OC.
分析:要证明OB=OC,只需要证明△ODB≌△OEC,垂直和对顶角已经提供了足够的角的信息,只需要再找一组对应边即可.利用角的平分线的知识得到OD=OE.
证明:∵AO平分∠BAC(已知),CD⊥AB,BE⊥AC(已知),
∴∠ODB=∠OEC=90°(垂直的意义),且OD=OE(在角的平分线上
的点到这个角的两边的距离相等).
在△ODB与△OEC中,
∴△ODB≌△OEC(A.S.A)
∴OB=OC(全等三角形的对应边相等).
(已证)
(已证)
(对顶角相等)
例题3 已知CD⊥AB,BE⊥AC,垂足分别是
点D、E;BE、CD相交于点O,且AO平分∠BAC.
求证:OB=OC.
练习 判断下面的证明过程是否正确,并说明理由.
已知:点D是射线AP上的一点,点E、F分别在AB、AC上,且DE=DF.
求证:AP平分∠BAC.
证明:∵点D是射线AP上的一点,且DE=DF(已知),
∴AP平分∠BAC(在一个角的内部且到角的两边距离相
等的点,在这个角的平分线上).
回答:错误.因为点到线的距离是由垂线段的长度表示的,
所以必须由垂直这个条件才能够使用角的平分线性质定理及其逆定理.
1.已知:如图,在 Rt△ABC中,∠C=90°,∠B=30°,AC=AE,AD 平分∠CAB,交BC于点 D,联结 DE,求证:DE是AB 的垂直平分线
课本练习
【解析】证明:∵AD平分∠CAB,∴∠DAE=∠CAD
∵AC=AE,AD=AD,∴△ACD≌△AED(SAS)
∴∠AED=∠C=90°∴DE⊥AB,
∵∠C=90°,∠B=30°,
∴∠BAC=90°-∠B=60°,
2.如图,在△ABC中,∠B-115°,AC 的垂直平分线与AB 交于点 D,联结 CD.如果∠BCD与∠DCA的度数比为3:5,那么∠ACB的度数是多少
【解析】设∠BCD、∠DCA的度数分别为3x,5x
∵AC的垂直平分线与AB交于点D,∴DA=DC
∴∠A=∠DCA=5x,
∵∠B=115°,∴∠A+∠ACB=180°-115°=65°
∴5x+5x+3x=65°,解得:x=5°
∴∠ACB=3x+5x=8x=40°
3.判断下面的证明过程是否正确,并说明理由.
已知:如图,点D是射线AP上的一点,点E、F分别在AB、AC上, DE=DF
求证:AP平分∠BAC.
证明:∵点D是射线AP上一点,且DE=DF(已知),
AP平分∠BAC(在一个角的内部且到角两边距离相等的点,在这个角的平分线上
【解析】错误。因为已知中缺少条件:DE⊥AB,DF⊥AC
1. 如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等.若∠A=40°,则∠BOC的度数为( )
A.110° B.120° C.130° D.140°
A
解析:由已知,O到三角形三边的距离
相等,所以O是内心,即三条角平分线
的交点,AO,BO,CO都是角平分线,
所以有∠CBO=∠ABO= ∠ABC,
∠BCO=∠ACO= ∠ACB,
∵∠ABC+∠ACB=180°-40°=140°,
∴∠OBC+∠OCB=70°,
∴∠BOC=180°-70°=110°.
随堂检测
2. 如图,某个居民小区C附近有三条两两相交的道路MN、OA、OB,拟在MN上建造一个大型超市,使得它到OA、OB的距离相等,请确定该超市的位置P.
小区C
P
A
O
B
M
N
3.已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,
点P在BM上,
∴PD=PE.
同理PE=PF.
∴PD=PE=PF.即点P到三边AB,BC,CA的距离相等.
D
E
F
A
B
C
P
N
M
M
E
N
A
B
C
P
O
D
4.如图,在直角△ABC中,AC=BC,∠C=90°,AP平分∠BAC,BD平分∠ABC,AP、BD交于点O,过点O作OM⊥AC,若OM=4.
(1)求点O到△ABC三边的距离和;
温馨提示:不存在垂线段———构造应用
12
解:连接OC.
M
E
N
A
B
C
P
O
D
4.如图,在直角△ABC中,AC=BC,∠C=90°,AP平分∠BAC,BD平分∠ABC,AP、BD交于点O,过点O作OM⊥AC,若OM=4.
(2)若△ABC的面积为32,求△ABC的周长.
5. 如图,在△ABC中,PE∥AB交BC于点E,PF∥AC交BC于点F,点P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
解:AD平分∠BAC.理由如下:
∵D到PE的距离与到PF的距离相等,
∴点D在∠EPF的平分线上.
∴∠1=∠2.
又∵PE∥AB,∴∠1=∠3.
同理,∠2=∠4.
∴∠3=∠4.∴AD平分∠BAC.
A
B
C
E
F
D
(
(
(
(
3
4
1
2
P
6.已知:如图,OD平分∠POQ,在OP、OQ边上取OA=OB,点C在OD上,CM⊥AD于M,CN⊥BD于N.求证:CM=CN.
证明:∵OD平分线∠POQ,
∴∠AOD=∠BOD.
在△AOD与△BOD中,
∵OA=OB,∠AOD=∠BOD,OD=OD,
∴△AOD≌△BOD.
∴∠ADO=∠BDO.
∵CM⊥AD,CN⊥BD,
∴CM=CN.
通过这节课的学习,你有什么收获和体会?
1.角的平分线的性质定理:
在角的平分线上的点到这个角两边的距离相等.
符号语言:
∵OP平分∠AOB
PD⊥OA,PE⊥OB,
∴PD=PE
(在角的平分线上的点到这个角两边的距离相等).
课堂小结
2.角平分线性质定理的逆定理:
在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上.
符号语言:
∴OP平分∠AOB
∵PD⊥OA,PE⊥OB,
PD=PE.
(在一个角的内部(包括顶点)且到角的两边
距离相等的点,在这个角的平分线上).
3. 三角形的三条角平分线交于一点,且这点到三边的距离相等.
D
E
F
G
H
S
∵∠1=∠2,∠3 =∠4,∠5=∠6
1
2
3
4
5
6
∴ AG、BH、 CS交于点O.
又 OD⊥BC, OE⊥AB, OF⊥AC,垂足分别为D、E、F,
∴ OD=OE=OF.
沪教版八年级上册
第 19 章 几何证明
19.5角的平分线(第2课时)
学习目标
1.进一步理解巩固线段的垂直平分线和角的平分线的性质定理;
2.能够应用角的平分线性质定理及其逆定理解决简单的几何问题;
3.通过探索和证明,发展推理意识和能力.
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
[知识回顾]
线段垂直平分线上的任意一点到这条线段两个端点的距离相等。
题设、结论
[“互逆”的思想]
逆命题
逆定理
定理
命题
逆命题
逆定理
定理
在角的平分线上的点到这个角的两边的距离相等。
在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上。
[知识回顾]
例题2 已知:CD垂直平分线段AB,E是CD上一点,分别联结CA、CB、EA、EB.[来源:]
求证:∠CAE=∠CBE.
分析:要证明∠CAE=∠CBE,可以通过△CAE≌△CBE来达到.也可以通过∠CAB-∠EAB=∠CBA-∠EBA来达到.
例题2 已知:CD垂直平分线段AB,E是CD上一点,分别联结CA、CB、EA、EB.[来源:]
求证:∠CAE=∠CBE.
证明:∵ CD垂直平分线段AB(已知),
∴EA=EB, CA=CB(线段垂直平分线上的任意
一点到这条线段两个端点的距离相等).
在△CAE与△CBE中,
(已证)
(已证)
(公共边)
∴△CAE≌△CBE(S.S.S).
∴∠CAE=∠CBE(全等三角形的对应角相等).
例题2 已知:CD垂直平分线段AB,E是CD上一点,分别联结CA、CB、EA、EB.[来源:]
求证:∠CAE=∠CBE.
另解:
证明:∵ CD垂直平分线段AB(已知),
∴EA=EB, CA=CB(线段垂直平分线上的任意一点到这条线段两个端点的距离相等).
∴∠CAB =∠CBA,∠1=∠2.(等边对等角)
∴∠CAB-∠1 =∠CBA-∠2.(等式性质)
即∠CAE=∠CBE.
例题3 已知CD⊥AB,BE⊥AC,垂足分别是
点D、E;BE、CD相交于点O,且AO平分∠BAC.
求证:OB=OC.
分析:要证明OB=OC,只需要证明△ODB≌△OEC,垂直和对顶角已经提供了足够的角的信息,只需要再找一组对应边即可.利用角的平分线的知识得到OD=OE.
证明:∵AO平分∠BAC(已知),CD⊥AB,BE⊥AC(已知),
∴∠ODB=∠OEC=90°(垂直的意义),且OD=OE(在角的平分线上
的点到这个角的两边的距离相等).
在△ODB与△OEC中,
∴△ODB≌△OEC(A.S.A)
∴OB=OC(全等三角形的对应边相等).
(已证)
(已证)
(对顶角相等)
例题3 已知CD⊥AB,BE⊥AC,垂足分别是
点D、E;BE、CD相交于点O,且AO平分∠BAC.
求证:OB=OC.
练习 判断下面的证明过程是否正确,并说明理由.
已知:点D是射线AP上的一点,点E、F分别在AB、AC上,且DE=DF.
求证:AP平分∠BAC.
证明:∵点D是射线AP上的一点,且DE=DF(已知),
∴AP平分∠BAC(在一个角的内部且到角的两边距离相
等的点,在这个角的平分线上).
回答:错误.因为点到线的距离是由垂线段的长度表示的,
所以必须由垂直这个条件才能够使用角的平分线性质定理及其逆定理.
1.已知:如图,在 Rt△ABC中,∠C=90°,∠B=30°,AC=AE,AD 平分∠CAB,交BC于点 D,联结 DE,求证:DE是AB 的垂直平分线
课本练习
【解析】证明:∵AD平分∠CAB,∴∠DAE=∠CAD
∵AC=AE,AD=AD,∴△ACD≌△AED(SAS)
∴∠AED=∠C=90°∴DE⊥AB,
∵∠C=90°,∠B=30°,
∴∠BAC=90°-∠B=60°,
2.如图,在△ABC中,∠B-115°,AC 的垂直平分线与AB 交于点 D,联结 CD.如果∠BCD与∠DCA的度数比为3:5,那么∠ACB的度数是多少
【解析】设∠BCD、∠DCA的度数分别为3x,5x
∵AC的垂直平分线与AB交于点D,∴DA=DC
∴∠A=∠DCA=5x,
∵∠B=115°,∴∠A+∠ACB=180°-115°=65°
∴5x+5x+3x=65°,解得:x=5°
∴∠ACB=3x+5x=8x=40°
3.判断下面的证明过程是否正确,并说明理由.
已知:如图,点D是射线AP上的一点,点E、F分别在AB、AC上, DE=DF
求证:AP平分∠BAC.
证明:∵点D是射线AP上一点,且DE=DF(已知),
AP平分∠BAC(在一个角的内部且到角两边距离相等的点,在这个角的平分线上
【解析】错误。因为已知中缺少条件:DE⊥AB,DF⊥AC
1. 如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等.若∠A=40°,则∠BOC的度数为( )
A.110° B.120° C.130° D.140°
A
解析:由已知,O到三角形三边的距离
相等,所以O是内心,即三条角平分线
的交点,AO,BO,CO都是角平分线,
所以有∠CBO=∠ABO= ∠ABC,
∠BCO=∠ACO= ∠ACB,
∵∠ABC+∠ACB=180°-40°=140°,
∴∠OBC+∠OCB=70°,
∴∠BOC=180°-70°=110°.
随堂检测
2. 如图,某个居民小区C附近有三条两两相交的道路MN、OA、OB,拟在MN上建造一个大型超市,使得它到OA、OB的距离相等,请确定该超市的位置P.
小区C
P
A
O
B
M
N
3.已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,
点P在BM上,
∴PD=PE.
同理PE=PF.
∴PD=PE=PF.即点P到三边AB,BC,CA的距离相等.
D
E
F
A
B
C
P
N
M
M
E
N
A
B
C
P
O
D
4.如图,在直角△ABC中,AC=BC,∠C=90°,AP平分∠BAC,BD平分∠ABC,AP、BD交于点O,过点O作OM⊥AC,若OM=4.
(1)求点O到△ABC三边的距离和;
温馨提示:不存在垂线段———构造应用
12
解:连接OC.
M
E
N
A
B
C
P
O
D
4.如图,在直角△ABC中,AC=BC,∠C=90°,AP平分∠BAC,BD平分∠ABC,AP、BD交于点O,过点O作OM⊥AC,若OM=4.
(2)若△ABC的面积为32,求△ABC的周长.
5. 如图,在△ABC中,PE∥AB交BC于点E,PF∥AC交BC于点F,点P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
解:AD平分∠BAC.理由如下:
∵D到PE的距离与到PF的距离相等,
∴点D在∠EPF的平分线上.
∴∠1=∠2.
又∵PE∥AB,∴∠1=∠3.
同理,∠2=∠4.
∴∠3=∠4.∴AD平分∠BAC.
A
B
C
E
F
D
(
(
(
(
3
4
1
2
P
6.已知:如图,OD平分∠POQ,在OP、OQ边上取OA=OB,点C在OD上,CM⊥AD于M,CN⊥BD于N.求证:CM=CN.
证明:∵OD平分线∠POQ,
∴∠AOD=∠BOD.
在△AOD与△BOD中,
∵OA=OB,∠AOD=∠BOD,OD=OD,
∴△AOD≌△BOD.
∴∠ADO=∠BDO.
∵CM⊥AD,CN⊥BD,
∴CM=CN.
通过这节课的学习,你有什么收获和体会?
1.角的平分线的性质定理:
在角的平分线上的点到这个角两边的距离相等.
符号语言:
∵OP平分∠AOB
PD⊥OA,PE⊥OB,
∴PD=PE
(在角的平分线上的点到这个角两边的距离相等).
课堂小结
2.角平分线性质定理的逆定理:
在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上.
符号语言:
∴OP平分∠AOB
∵PD⊥OA,PE⊥OB,
PD=PE.
(在一个角的内部(包括顶点)且到角的两边
距离相等的点,在这个角的平分线上).
3. 三角形的三条角平分线交于一点,且这点到三边的距离相等.
D
E
F
G
H
S
∵∠1=∠2,∠3 =∠4,∠5=∠6
1
2
3
4
5
6
∴ AG、BH、 CS交于点O.
又 OD⊥BC, OE⊥AB, OF⊥AC,垂足分别为D、E、F,
∴ OD=OE=OF.
